基于MGWO-SD模型的户用光伏装机容量预测研究

孙乐平，郭小璇，李景顺，刘朋超，杨小林

(1.广西电网有限责任公司电力科学研究院，广西 南宁 530023；2.广西电网有限责任公司桂林供电局，广西桂林 541002；3.重庆大学 电气工程学院，重庆 400044）

0 引言

随着分布式光伏和户用光伏市场的快速发展[1]，针对户用新增光伏装机容量进行预测研究，有利于明确户用光伏市场的投资潜力，实现对户用光伏市场投资的风险规避，同时，监测光伏市场的动态变化，可为分布式光伏总装机预测提供参考，保障区域电网的安全运营和新型电力系统建设的合理规划。

国内外已有部分学者针对未来几年分布式及户用光伏装机容量的发展进行了预测研究。文献[2]通过小世界网络模型模拟了从众心理对用户投资决策的影响，解释了光伏装机规模与投资回报率间的非线性复杂关系，提高了系统动力学(System Dynamics，SD）模型的预测精度。文献[3]利用SD理论搭建了预测模型，但并未考虑居民用电量的增长及贷款成本等直接影响用户投资回报率的相关因素。文献[4]结合双因素学习曲线和理性决策模型，在SD模型中分析了不同激励政策对光伏装机规模扩散速度的影响程度。文献[5]利用SD模型模拟了政策影响下中国光伏发电的发展趋势，且对关键变量进行了敏感性分析，但模型中仅将其他新能源发电量设为外生变量，并未考虑其与光伏发电产业间的深层次影响关系。

传统的SD预测方法不能很好地适应各种非线性预测问题，基于此，有学者提出引入智能算法进行优化，以便提高预测精度。文献[6]在极限学习机中采用遗传算法，搜索隐偏差和输入权值的最优值，从而提高了光伏功率输出的预测精度。文献[7]提出了一种基于精英反向策略改进的麻雀搜索算法，优化极限学习机的光伏短期输出功率预测模型，对于不同天气状况的功率预测精度高。文献[8]将自适应粒子群优化算法和最小二乘支持向量机相结合，使得模型具有较好的跟踪模式性 能。灰 狼 优 化[9](Grey Wolf Optimizer，GWO）算 法以参数少、寻优快等优点在各领域得到广泛应用，可以更好地提升预测精度与速度，但面对不同的实际问题，容易出现早熟收敛和陷入局部极值的风险，国内外很多学者做出了改进。文献[10]提出了一种在非线性双收敛因子策略下双头狼引领的灰狼算法，在多峰函数上收敛性表现极为优异。文献[11]引入了一种基于维度学习的搜寻策略，使用不同的方法为每只狼构建一个邻居，能够实现信息共享，增强了局部收敛和全局搜索之间的平衡性。

基于上述研究，本文为了对户用分布式光伏发展进行合理预测，搭建了考虑学习效应、政府补贴等影响因素的户用光伏装机容量SD模型，并基于改进灰狼优化(Modified Grey Wolf Optimizer，MGWO）算法对预测模型进行参数优化，最终构建基于MGWO-SD的户用光伏装机容量预测模型，并与传统的GWO算法优化后的系统动力学(GWO-SD）模型以及现有模型进行对比分析。结果表明，本文提出的MGWO-SD装机容量预测模型具有较高的精确度，可为后续光伏产业发展提供参考。

1 系统动力学预测模型

1.1 模型搭建分析

本文以户用光伏装机容量为研究对象，综合考虑了度电补贴、居民销售电价、脱硫煤电价等直接影响户用光伏售电总收益的因素，构建了户用光伏装机容量的系统动力学预测模型，不同变量间的因果反馈关系通过箭头连接表示，即某一变量的增减会引起与之关联的变量发生变化，如图1所示。

本文所搭建的模型将户用光伏累计装机容量设为主要的状态变量(即存量变量），它所对应的流量变量(也称速率变量）为每年新增装机容量，其余如投资回报率、用户装机意愿、光伏发电总成本等部分则为辅助变量，各变量之间的影响机制如下。

①以每年年底统计的户用光伏累计装机容量作为累积量，流量则为目标年新安装的装机容量，而目标年的新增装机容量主要受上一年的新增装机容量与目标年用户的装机意愿两大因素的影响，因此要确定某一年份的新增装机容量，必须计算该年份用户群体的实际安装意愿。

②用户安装户用光伏发电系统的意愿取决于光伏项目的实际经济效益，当投资项目的回报满足或超过用户预期，即项目的实际投资回报率越高，投资回收年限越短，用户的投资积极性就越强烈，当年的新增装机容量随之也越多。

③对于户用光伏用户，既可以通过 “自发自用，余电上网”、“全额上网”等模式来节省电费或销售发电量，还可在两种并网模式获取电价收益基础上，通过国家给予的度电补贴获利，这两者共同构成了户用光伏投资年收益。发电收益与度电补贴、销售电价及上网电价等因素直接相关，而它们通常会随着政府或电网的相关文件进行一定调整，使收益不断波动变化，进而影响用户的投资意愿。

④通常，投资成本主要由初始投资成本(即装机成本）、运营成本及贷款成本组成，而根据光伏产业的学习效应，装机成本通常会随着光伏累计装机规模的扩大呈逐渐下降趋势，即装机容量的增长会反过来导致投资成本的变化，从而形成了装机容量与投资回报率间的反馈回路。

1.2 各模块具体建模

本文所搭建的系统动力学模型主要分为收益模块、成本模块、装机意愿模块、装机容量模块共4个模块，以下为各个模块的具体建模过程。

1.2.1收益模块

本文所搭建的系统动力学模型中收益模块主要为发电收益。

目前，我国户用光伏可分别通过“余电上网”和“全额上网”两种方式获得收益。用户通过“余电上网”获得的发电收益分为：①省下的家庭用电缴纳费用；②电网按照当地脱硫煤电价收购剩余发电量的回购收益；③政府对户用光伏发电附加的度电补贴。因此，“余电上网”用户发电收益可表示为

式中：Gs(t）为第t年通过余电上网获得的发电收益；Ech为家庭年均用电量；Ts为居民生活用电的销售电价；Pgh为户用光伏年均发电量；St为国家通过可再生能源发展基金给予的度电补贴；Tdes为脱硫煤电价。

相对于“余电上网”，用户通过“全额上网”获得的发电收益中没有节电收益这一项，其表达式为

式中：Gf(t）为第t年通过全额上网获得的发电收益；Tbm为光伏标杆上网电价。

设居民用户中通过“全额上网”获得收益的比例为ρ，则根据上述分析，第t年户用分布式光伏所能获得的年总收益G(t）为

1.2.2成本模块

我国家庭投资户用光伏发电系统的总成本通常由初始投资成本、贷款成本及运营成本等部分组 成[12]，即：

式中：CH(t）为第t年的户用光伏发电总成本；Cinv(t），Cop(t），Ccr(t）分 别 为 第t年 的 初 始 投 资 成 本、运营成本与贷款成本。

初始投资成本主要涵盖光伏组件及并网逆变器等设备的购置费用、系统设计费用与安装费用等相关费用[13]。光伏系统的初始投资成本随着光伏产业规模的扩大而逐渐降低，国内外学者常用学 习 效 应 曲 线 描 述 这 一 现 象[14]，[15]，即：

式中：Cinv0为选择的基准年初始投资成本；I(t）为第t年的户用光伏累计装机容量；I0为基准年的户用光伏累计装机容量；λ为弹性系数；Rl为学习率(Learning Rate），它表示当户用光伏的装机容量每增长一倍时，初始投资成本将降低到之前的1-Rl。

运营成本按照初始投资成本的一定比例估算[16]，设 运 营 费 率 为rop，则 有：

假设初始投资成本中贷款比例为Pl，银行利率为γ，则贷款成本应为

1.2.3装机意愿模块

研究表明，投资项目的实际投资回报率与期望投资回报率之比直接影响用户的投资决定[3]，对于户用光伏发电项目，用户的装机意愿可表示为

式中：Wi(t）为第t年用户投资户用光伏发电项目的装机意愿；R(t）为第t年户用光伏发电项目的实际投资回报率；Rq为用户所期望的投资回报率。

投资回报率定义为项目年收益与投资总成本之比，根据上述分析，户用光伏发电项目的实际投资回报率应为

1.2.4装机容量模块

每年的户用光伏累计装机容量I(t）应为上一年的累计装机容量I(t-1）与该年新增装机容量In(t）之和，而某一年份新增装机容量则正比于该年装机意愿与上一年份的新增装机容量的乘积[4]，即：

2 改进灰狼优化算法

由于某些参数设定没有准确标准，为了预测结果的可靠性，利用改进灰狼优化算法进行参数优化。GWO算法[9]是根据灰狼群体的等级制度和捕猎方式提出的群体仿生类算法。灰狼群体中存在严格的社会等级关系，可划分为α狼、β狼、δ狼和 ω狼，如图2所示。其中 α狼、β狼和 δ狼为灰狼种群中的三种精英狼，α狼最大程度上决定狼群的行为方式，其次是β狼与δ狼，均服从上级狼支配。在寻找猎物过程中，α狼、β狼和 δ狼负责追踪猎物和引导狼群，而 ω狼的行动受他们支配，逐渐接近猎物并发起攻击。

图2 灰狼的等级制度Fig.2 Hierarchy of grey wolf

精英狼追踪猎物的数学模型表示为

式中：D为搜索步长；i为迭代次数；A，C为扰动因子；Xp为猎物的位置向量；X为灰狼的位置向量；rand(）为0～1的随机数；a为收敛因子；随迭代次数递减。

狩猎通常是由 α狼主导，β狼、δ狼可能参与狩猎。然而在未知的搜索空间，无法知道最优位置，为了从数学上模拟灰狼的捕食行为，保存前3个最优解并使得 ω狼在根据最佳搜索位置来更新其自身位置。更新公式如下：

式 中：Dα，Dβ和Dδ分 别 为 α狼、β狼 和 δ狼 的 搜 索步 长；Xα(i），Xβ(i）和Xδ(i）分 别 为 当 前 α狼、β狼 和δ狼 的 位 置；Xk(i）为 ω狼 的 位 置；Xj(i+1）(j=1，2，3）为 精 英 狼 引 导 后 的 位 置；A1，A2，A3与C1，C2，C3为扰动因子。

标准GWO算法中收敛因子a采用线性递减策略。当|A|≥1时，精英狼始终与当前猎物位置保持一定距离并在附近范围内持续搜索，对应于全局搜索阶段。当|A|﹤1时，精英狼开始引导狼群向猎物位置靠近，对应于局部搜索阶段，而A的取值与收敛因子a密切相关。由于预测问题是一个非线性问题，若将收敛因子改为非线性递减的函数，能更有效地提升户用光伏装机容量预测精度。本文引入新的收敛因子。

式中：am为改进后的收敛因子；Iter为最大迭代次数；e为自然常数。

设置最大迭代次数为100次，分别利用GWO算法和MGWO算法优化SD模型，原始的GWO算法和MGWO算法的收敛因子如图3所示。根据迭代过程中两种算法的收敛因子变化曲线可以看出，在迭代初期，MGWO算法相对于GWO算法能更好地进行全局搜索，在迭代后期能更好地进行局部搜索，有效地提高了搜索范围和搜索精度。

图3 GWO和MGWO算法的收敛因子Fig.3 Comparison of convergence factors between GWO and MGWO

图4为本文基于MGWO算法优化SD模型的流程图，其中，目标函数为预测结果与实际值的 均 方 根 误 差(Root-Mean-Square Error，RMSE）。RMSEbest，RMSEmin，RMSEi分 别 为 全 局 最 小 均 方 根值，当前最小均方根值和第i次迭代的均方根值。

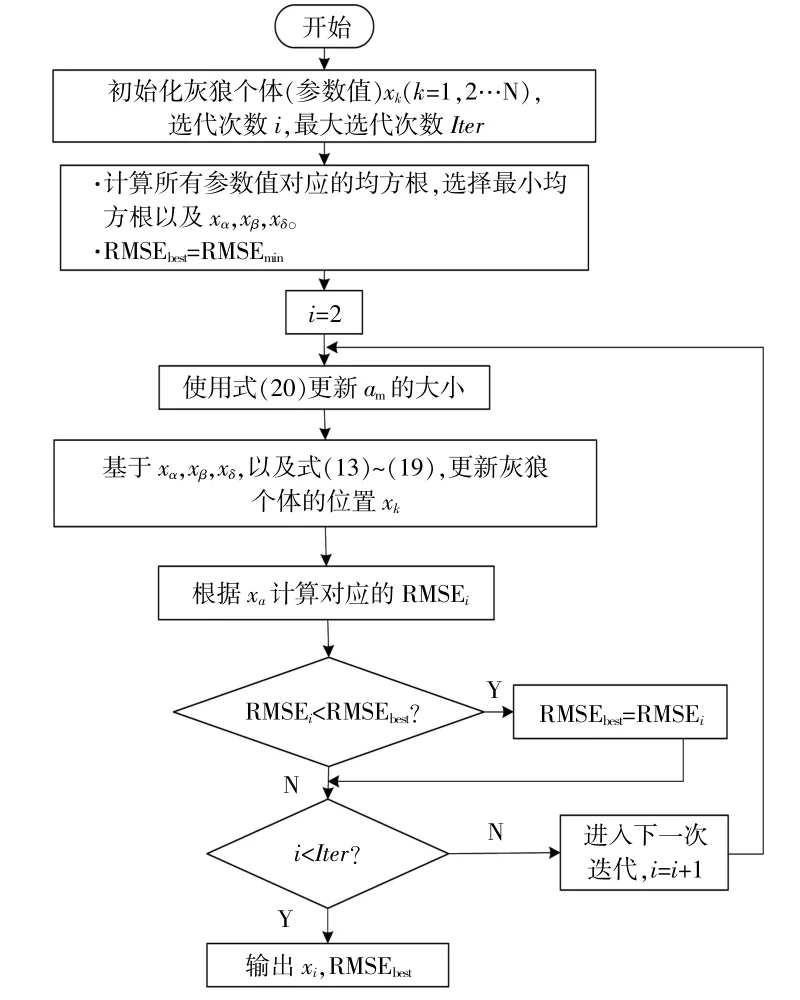
图4 基于MGWO算法优化SD模型的流程图Fig.4 Flow chart of SD model optimization based on MGWO algorithm

式 中：I′(t）和I(t）分 别 为 第t年 累 计 装 机 容 量 的预测值和实际值；n为预测年限。

3 算例分析

本文使用Vensim PLE软件搭建了基于系统动力学理论的户用分布式光伏装机容量预测模型，然后利用国家能源局所公布的数据和MGWO算法对仿真参数进行设定及寻优，将本文所提方法与其他预测方法进行了对比，并利用该模型预测了华东A省2017-2027年的户用光伏装机规模及初始投资成本的发展趋势，且对仿真结果进行了分析研究。

3.1 参数设定

根据A省物价局发布的相关政策文件，确定A省近5a的居民销售电价与脱硫煤电价始终保持 为0.528 3元/(kW•h）与0.391 0元/(kW•h）；根据“发改价格[2016]2729号”等文件，仿真初始年2017年A省的光伏标杆电价应取0.85元/(kW•h），户用光伏度电补贴标准则取0.42元/(kW•h），2018-2020年的数据同样可以根据相关文件得到，而2021年及之后的光伏标杆上网电价则按照“脱硫煤基准价+上下浮动”的方式模拟上网电价变化。

根据国家能源局公布的相关数据，2017-2021年A省户用分布式光伏累计装机容量分别约 为587.30，742.37，939.97，1 193.95，1 633.70 MW。本文查询了近几年A省各市区光伏年有效利用小时数，计算得出该地区单位装机年平均发电量约为1 107.26 kW•h，且根据我国户用光伏实际安装条件，将每户光伏平均安装容量设置为5 kW；同样利用A省统计局发布的城乡居民总用电量，按照每户3人的家庭规模拟合得到2017-2022年模型居民家庭平均用电量。

将2017年的装机成本选为基准年初始投资成本，根据市场调查报告，2017年我国户用光伏设备购置成本约为6元/W，再考虑发电装置的安装与设计费用，最终将初始投资成本取为6.2元/W。而根据目前市场经营状况与相关研究[17]，光伏发电项目的贷款比例为35%～70%[18]，银行贷款利率为3.5%～6.5%，项目期望投资回报率则普遍为5%～15%[19]，对于此类难以具体确定的变量，本文利用MGWO算法进行了参数寻优。

综上分析，本文所搭建的预测模型初始参数设置见表1。

表1 模型参数初值设定Table 1 Initial value setting of model parameters

3.2 仿真分析与方法对比

由于期望投资回报率、运营费率、银行利率和采用全额上网的用户比例在系统动力学模型中很难确定参数的数值，因此采用智能算法进行寻优。GWO算法和MGWO算法优化参数收敛过程对比见 图5。

图5 GWO算法和MGWO算法收敛过程图Fig.5 Comparison of convergence process between GWO algorithm and MGWO algorithm

由图5可见，改进后的灰狼优化算法相较于传统的灰狼优化算法更快到达收敛，同时得到不同寻优算法下4个参数的取值，见表2。

表2 GWO算法和MGWO算法优化后的参数取值Table 2 Parameter setting optimized by GWO algorithm and MGWO algorithm

为评估实际预测效果，将本文所搭建的MGWO-SD预测模型与其他2种预测方法(灰色系统法和二次指数平滑预测法）进行对比，结果见图6。

图6 户用光伏装机容量初步预测结果Fig.6 Preliminary prediction results of household PV installed capacity

表3列出了MGWO-SD的预测值和实际值。

表3 MGWO-SD模型的预测结果Table 3 Prediction results of the MGWO-SD model

为进一步衡量模型预测精度，本文同时计算了平均绝对百分误差(Mean Absolute Percentage Error，MAPE）和 均 方 根 误 差(RMSE），分 别 评 估 预测结果的相对误差和绝对误差，见表4。

表4 不同预测模型下平均绝对百分数误差和均方根误差Table 4 MAPE and RMSE under

从 式(21）和 式(22）可 见，MAPE与RMSE分别通过绝对值与平方避免了正负误差的相互抵消，进而准确衡量了预测结果与实际数据的相对及绝对偏差，因此通过这两类误差指标能够更好地评估不同方法的预测精度。

由图6和表3可见，本文所使用的方法预测得到A省2018-2021年户用光伏累计装机容量分 别 为733.83，929.63，1 203.50，1 631.74 MW，与实际数据的相对误差均低于1.5%，均方根误差为7.413 9 MW，显著低于二次指数平滑法与灰色预测法的均方根误差(分别为120.504 9，30.358 4 MW）。本文所搭建的户用光伏装机容量预测模型精度较高，更符合产业发展规律。此外，由表4可知，本文所提出的MGWO-SD模型与其他模型相比，MAPE，RMSE均表现得最为优异，与二次指数平滑法和灰色预测法相比，其预测精度大大提高。虽然与GWO-SD模型最终预测的误差波动相差不大，但其收敛速度始终快于GWO-SD预测模型，证明了本文所提改进灰狼优化算法在户用光伏装机容量预测研究中具有良好的优势。

综上，本文所提出的MGWO-SD装机容量预测模型具有较高的精确度，在此基础上，进一步利用该模型对2017-2027年华东A省户用光伏累计装机容量与初始投资成本的发展趋势进行了预测分析，其结果如图7所示。

图7 户用光伏累计装机容量及成本发展趋势Fig.7 Development trend of household PV cumulative installed capacity and cost

由图7可见，虽然自2018年我国开始逐步减小分布式光伏发电补贴力度，但随着光伏产业学习效应的进一步加深，光伏组件成本的降低能够及时补足快速下调的光伏补贴所引发的收益缩水，使得户用光伏的投资回报率始终保持在较高水平，进而保证户用光伏装机容量持续稳步增长，预计到2027年将达到5 261.8 MW。

此外，光伏装机容量的快速增长刺激着光伏组件生产厂家对产品规模的扩大，而在生产过程中由于技术的不断进步与经验的逐渐累积，单位产品的制造成本会逐年降低，最终使得光伏组件购置成本与装机容量之间以学习效应曲线的趋势下降。图7可见，预计2027年初始投资成本将由6.2元/W降低至约2.3元/W，这将直接刺激户用光伏装机规模的扩大。

4 结论

本文搭建了户用分布式光伏装机容量预测模型，将系统动力学模型与改进灰狼优化算法结合，建立了MGWO-SD预测模型。所搭建的模型精度相对于其他模型而言，能够准确地预测我国户用分布式光伏装机容量的中长期发展趋势，其平均绝对百分数误差和均方根误差分别为0.634 0%与7.413 9 MW，在多种预测方法中表现最为优异。本文所提的改进灰狼优化算法在原始GWO算法的基础上，提高了收敛速度和收敛精度，为后续大规模预测户用光伏装机容量打下基础。