基于无轨道密度泛函理论的金属钠板系统能量泛函*

刘润凤,胡奇宏,周 芳,程晓迪,王小云,黄勇刚

(吉首大学物理与机电工程学院,湖南 吉首 416000)

密度泛函理论(Density Functional Theory,DFT)能够准确描述各种材料的基态性质,是计算凝聚态物理电子结构的重要方法[1-2].然而,DFT的计算成本与体系中电子数量的立方成正比,因此往往仅能用于处理具有周期结构或者超小规模的体系,而对于大规模多电子体系,DFT的应用受到极大限制.相比之下,无轨道密度泛函理论(Orbital-Free Density Functional Theory,OF-DFT)的计算成本较低,其实质可以看作是只考虑最小特征值的自恰Kohn-Sham方程[3-6],能直接通过电子密度计算总能量,因此可以突破DFT在模拟尺度上的极限.OF-DFT的主要优点是线性缩放计算成本,可应用于非常大的系统.此外,在有限元方法中实施OF-DFT,进一步扩展了OF-DFT的应用广泛性[7].将OF-DFT与有限元方法结合,可以实现对各种具有复杂形貌特征的金属体系的基态性质的精确计算.基于此,笔者拟采用OF-DFT对金属钠板基态性质进行深入探讨.

使用OF-DFT计算体系的基态密度和功函数时,能量泛函的选择至关重要,它直接影响方法的准确度.能量泛函由动能泛函和交换关联泛函组成,目前相关研究工作中,许多近似的动能泛函被用于描述体系的相互作用能[4-5,8-10].最常采用的动能泛函是由Thomas-Fermi (TF) 和von Weizsacker (vW)组合而成的TFvW动能泛函,交换关联泛函通常采用基于局域密度近似(Local Density Approximation,LDA)的交换关联势[7,11-12].虽然TFvW动能泛函被广泛采用,但vW动能泛函缺乏微观对应,其比重尚未确定.研究发现,vW动能泛函的比重越大,电子溢出效应越明显,溢出功也越大[13],因此确定vW动能泛函的比重成为一个亟待解决的问题.另外,虽然不同的LDA交换关联势被广泛采用[7],但其对计算结果的影响尚不明确.

为了确定金属钠板获得准确基态性质所需的vW动能泛函,笔者首先研究了OF-DFT及DFT的相关理论和模型,并介绍了计算基态密度和功函数的方法,进一步研究了vW动能泛函的比重在不同LDA交换关联泛函中对基态密度误差与功函数误差的影响.

1 理论与模型

1.1 无轨道密度泛函理论

在OF-DFT中,通常通过求解欧拉方程来获得体系的基态性质[4-5,14-15],即

(1)

其中:n表示基态密度;φ0表示静电势;μ表示化学势.能量方程G[n]包含电子系统相互作用的动能(Ts)和交换相关能(EXC),即

G[n]=Ts[n]+EXC[n].

(2)

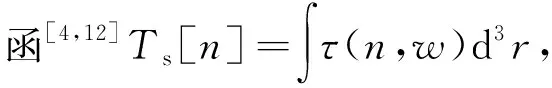
τ(n,w)=τvW(n,w)+τTF(n),

其中

τvW(n,w)=An-1w,

τTF[n]=Bn5/3.

为了求解(1)式,对方程式两侧做梯度运算,即

(3)

其中E0表示静电场.(3)式称为量子流体动力学静态方程.将(3)式与Maxwell方程耦合,可得

(4)

其中n+表示正电荷密度.在凝胶模型中,正电荷密度在球体内是均匀恒定的,而在球体边缘外部突然下降至0.将(3)式与(4)式结合,可得

(5)

通过(5)式可以计算体系的基态密度.本研究中,所有的OF-DFT计算都使用有限元(FEM)软件COMSOL的弱形式模块来实现.

1.2 OF-DFT中能量泛函对基态性质的影响

图1 金属钠无限大平板示意Fig. 1 Schematic Diagram of an Infinite Plate of Sodium Metal

使用OF-DFT计算金属钠无限大平板的基态密度和功函数,并将结果与DFT计算结果进行对比.假定无限大平面在y轴和z轴方向无限大,在x轴方向的厚度为L,那么本研究只需关注无限大平面在x轴方向上的基态性质即可.金属钠无限大平板模型如图1所示.

首先研究OF-DFT中不同能量泛函对基态密度和功函数的影响.图2和图3的纵轴使用对数坐标,这可以明显比较基态密度在金属边界处的衰减速度.不同vW动能泛函比重对基态密度的影响如图2所示.图2中,交换关联势均使用了LDA-WG.从图2可知,随着λ的逐渐增大,基态密度的衰减速度逐渐降低.在对数坐标下,基态密度在金属边界处的衰减近似为稳定的直线,这说明基态密度在金属表面的衰减可以看作近似e指数衰减[11].vW动能泛函的比重可以调控这一衰减因子,vW动能泛函比重越大,衰减因子越小,则基态密度在金属边界处的衰减速度越慢,体系的溢出效应越明显.不同LDA交换关联势对基态密度的影响如图3所示.图3中,参数vW动能泛函比重取值为1.从图3可知,由LDA-WG,LDA-PZ和LDA-GL计算得到的基态密度几乎没有明显区别,即使使用了对数坐标,差距仍然较小.

以上结果说明,vW动能泛函的比重会影响基态密度的计算结果.vW动能泛函比重的增加,实质上可以理解为增加了体系的电子溢出效应,因此基态密度的衰减速度也会受到影响.相比之下,选择不同的LDA交换关联势对基态密度的影响较小.

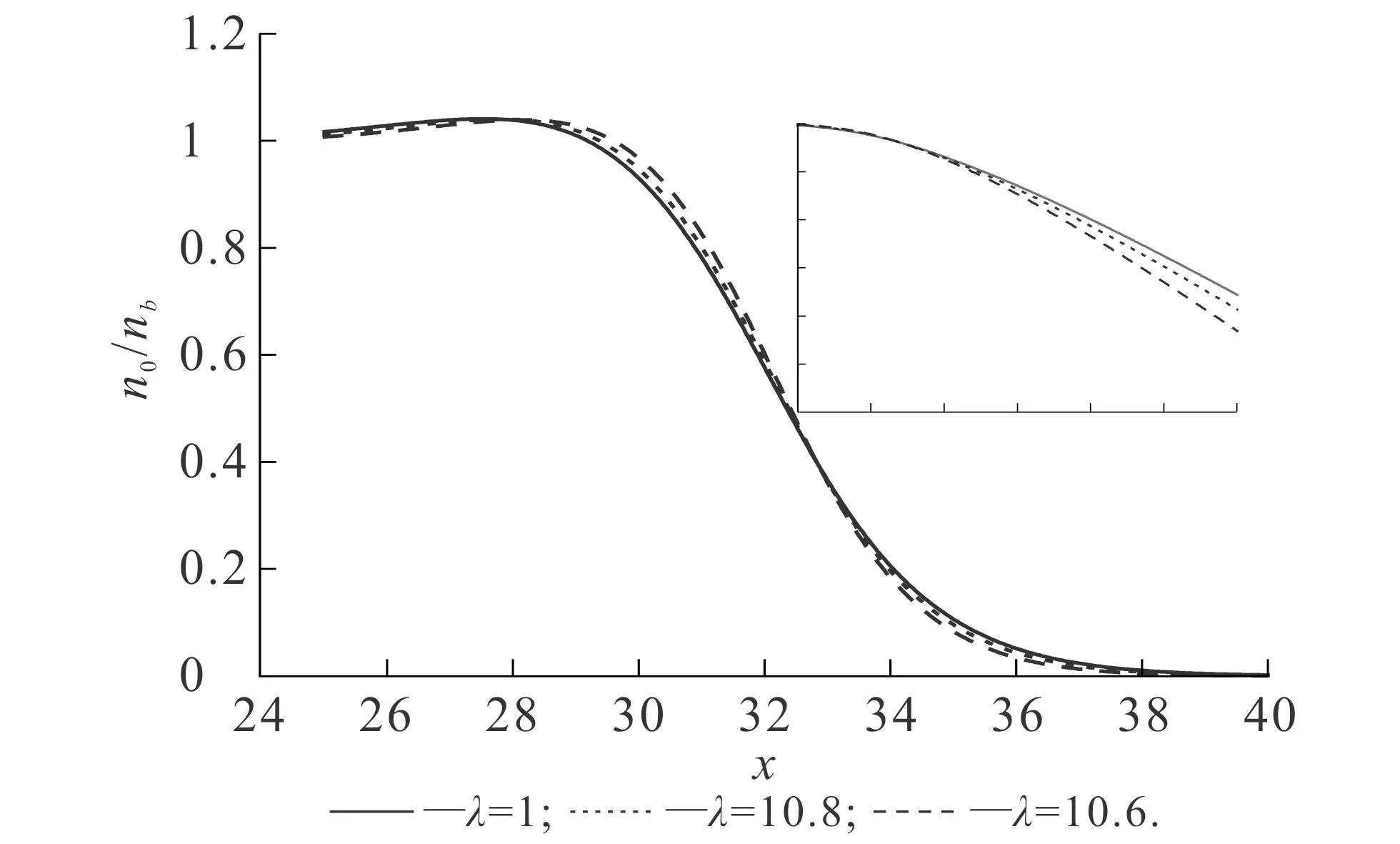
图2 不同vW动能泛函比重对基态密度的影响Fig. 2 Ground State Densities Obtained with Different vW Kinetic Energy Functional Proportions

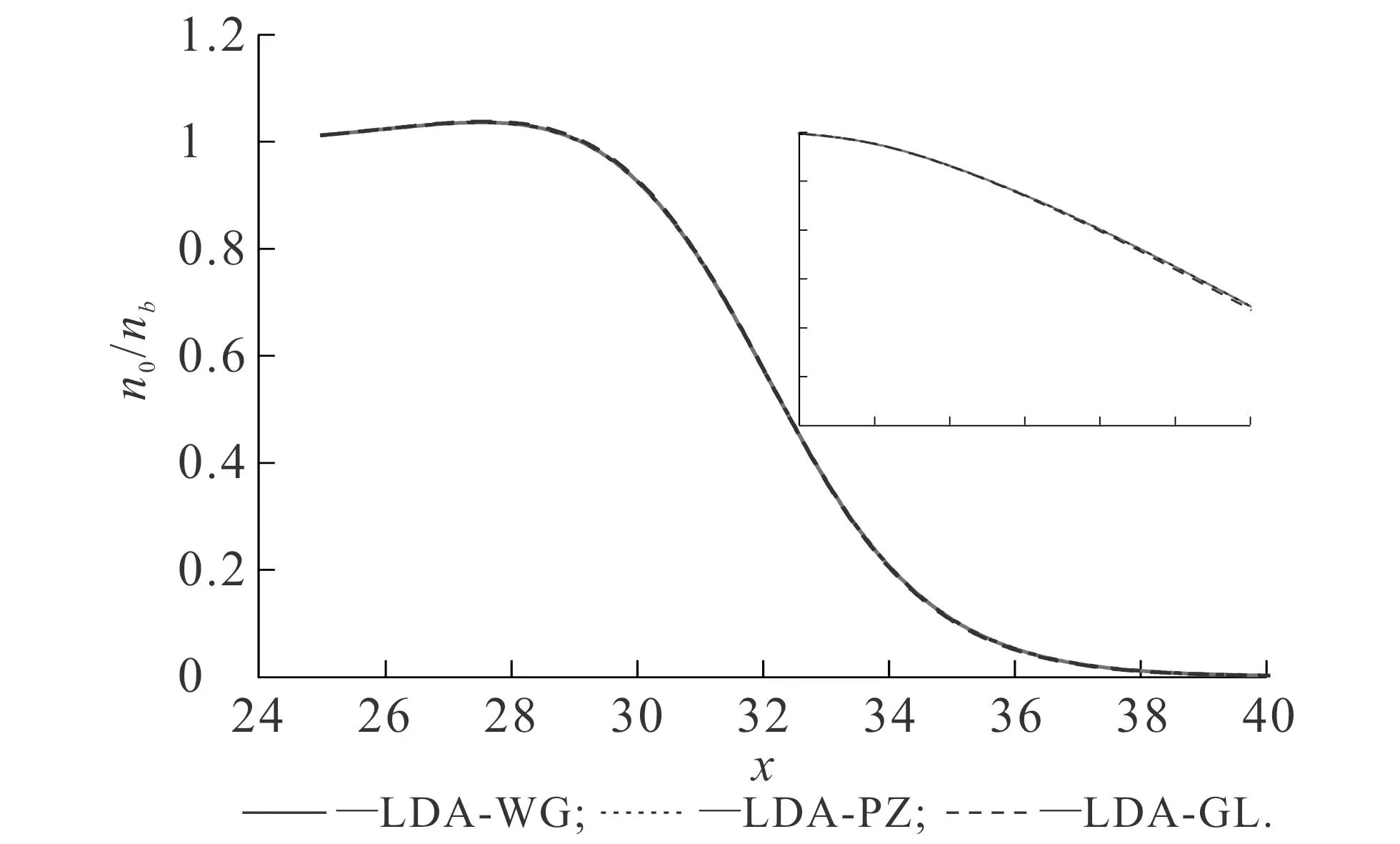
图3 不同LDA交换关联势对基态密度的影响 Fig. 3 Ground State Densities Obtained with Different LDA Exchange-Correlation Potentials

另一方面,功函数同样是重要的基态性质.接下来笔者介绍使用OF-DFT求解功函数的方法.OF-DFT可以看作是只考虑最小特征值的自恰Kohn-Sham方程,由于OF-DFT中只考虑最小的特征值,体系中所有电子能量相同,因此(1)式中的化学势(μ)即为体系功函数,即

W=Ts[n]+EXC[n].

(6)

根据功函数的定义,(6)式需取无穷远处的值.利用(6)式计算得到的化学式,其在空间各处皆为常数.不同vW动能泛函比重对功函数的影响如图4所示.图4中交换关联势均使用了LDA-WG.从图4可知,功函数随着λ的增大而增大,λ由0.6增大至1.0时,功函数由3.218 eV增大至3.538 eV.不同交换关联势对功函数的影响如图5所示.图5中,参数vW动能泛函比重值为1.由图5可知,LDA-WG,LDA-PZ和LDA-GL计算得到的功函数分别为3.538,3.478,3.368 eV.

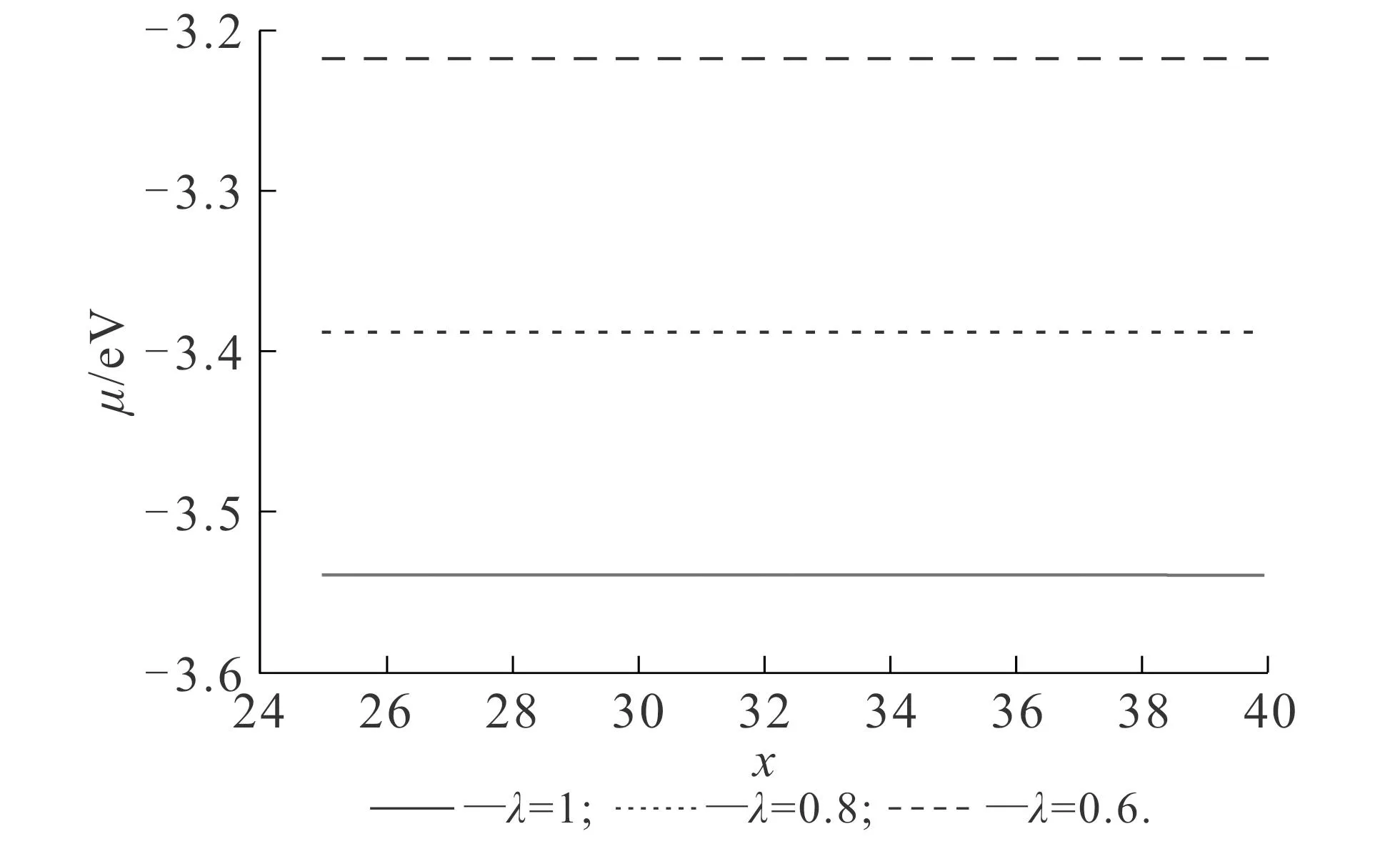
图4 不同vW动能泛函比重对功函数的影响Fig. 4 Work Functions Obtained by Different vW Kinetic Energy Functional Proportions

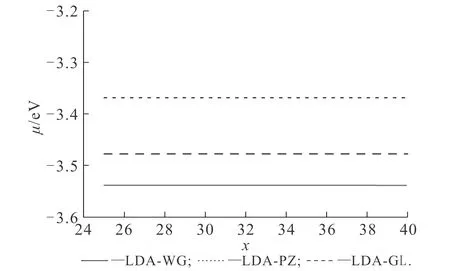
图5 不同LDA交换关联势对功函数的影响Fig. 5 Work Functions Obtained by Different LDA Exchange-Correlation Potentials

计算结果说明,vW动能泛函比重和交换关联势的改变都会影响功函数的计算结果.与上述基态密度的变化类似,vW动能泛函比重的增加,实质上可以理解为增加体系的电子溢出效应,从而引起功函数增加.此外,笔者发现,与基态密度不同,交换关联势的改变会影响功函数的计算结果,原因在于交换关联势在远场起主要作用.

1.3 密度泛函理论

为了验证OF-DFT计算结果的准确性,使用开源软件OCTOPUS计算DFT模块[16-17],并将DFT计算结果与OF-DFT计算结果进行对比.在碱金属中,价电子的费米波长远大于金属晶格常数,离子的赝势对电子结构没有显著影响.因此,可以用均质的正电荷背景代替离散的离子结构,即使用凝胶模型[18-20].此时,金属板钠体系可以看作是Wigner-Seitz半径(rs)为4的凝胶模型,进一步求解Kohn-Sham方程,这一处理能极大节省计算资源.在OCTOPUS中,可以使用不同的交换关联势,为了能与动能泛函在OF-DFT中的作用进行比较,本研究使用与OF-DFT一致的交换关联势.

DFT中,不同LDA交换关联势下基态密度计算结果如图6所示.从图6可知,与OF-DFT类似,DFT中使用不同交换关联势计算得到的基态密度并无较大差别.不同LDA交换关联势下功函数计算结果如图7所示.这类计算在文献[21-23]中已出现过.从图7可知,功函数呈现振荡行为,其原因在于随着平板厚度的逐渐增加,闲带的能量逐渐变低,在一定的平板宽度上,各自的最低闲带接触并最终穿过费米曲面.这些接触点以λF/2的周期出现(λF≈3.27rs),笔者观察到,功函数在λF=8时基本达到稳定振荡.若进一步增加平板厚度,则需要更多的计算资源,同时会导致收敛困难,因此在本研究中,选择λF=9.5和λF=10时的平均值作为DFT计算得到的功函数,这一方案获得的研究结果与文献[14]完全一致.使用LDA-WG,LDA-PZ和LDA-GL交换关联势计算得到的功函数分别为3.051,2.910和3.025 eV,这说明交换关联势对功函数依然有较大影响.

图6 DFT中不同LDA交换关联势对基态密度的影响Fig. 6 Ground State Density Calculated for Different LDA Exchange-Correlation Potentials in DFT

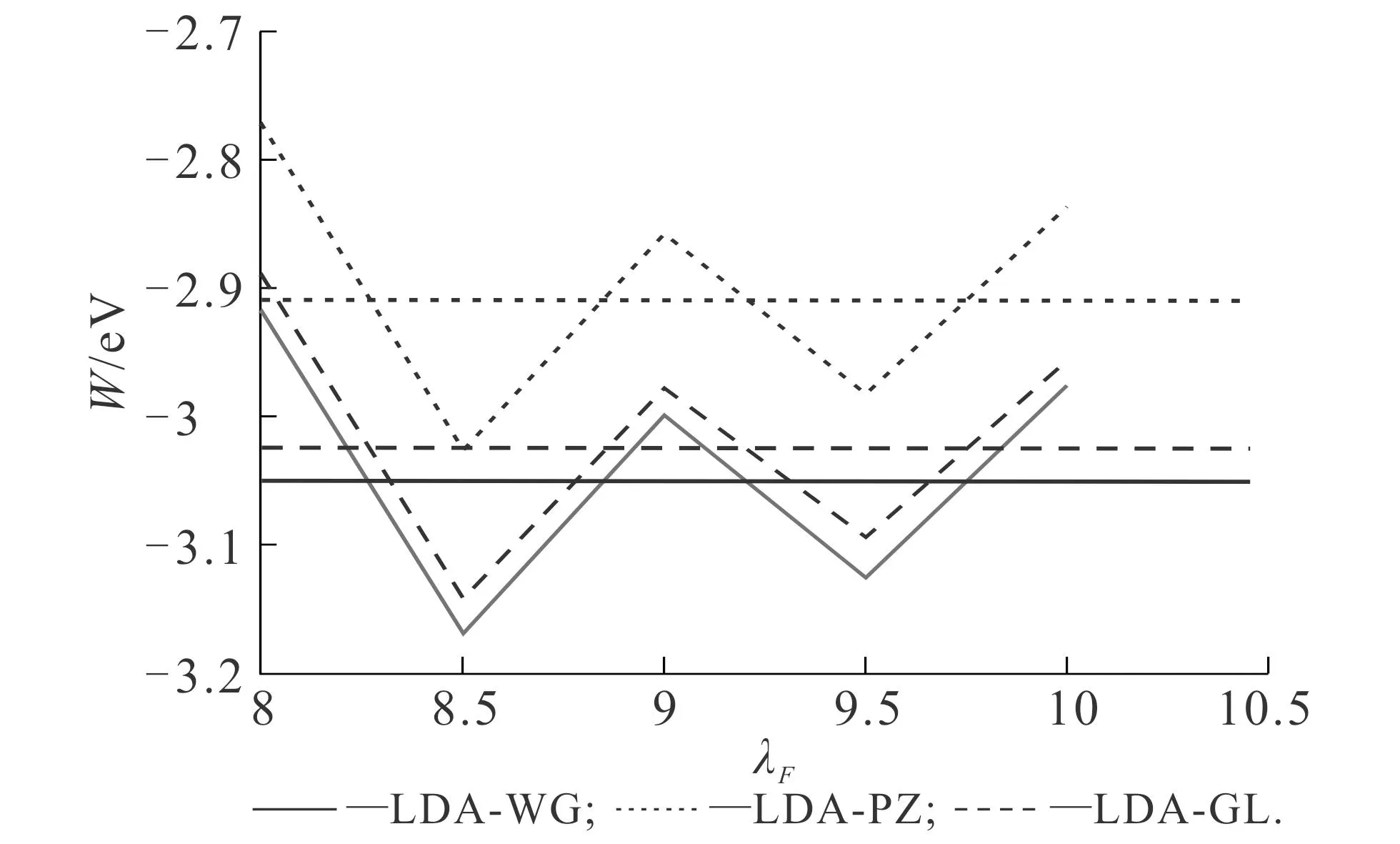
图7 DFT中不同LDA交换关联势对功函数的影响Fig. 7 Work Function Calculated for Different LDA Exchange-Correlation Potentials in DFT

1.4 功函数误差和基态密度误差

笔者计算了不同动能泛函的基态密度误差[4],计算公式为

(7)

其中S表示任意选择的有限表面积,方程右侧分母表示有限体积中的电子总数.(7)式中的基态密度误差可以看作是单个电子的平均基态密度误差.功函数误差

其中i=1,2,3,代表3种不同的相关势,即WG,PZ,GL相关势.需要注意的是,在对比中要保持选择的交换关联势一致.下面笔者将重点比较OF-DFT中不同动能泛函的功函数误差与基态密度误差,探寻金属板钠体系的最优能量泛函.

2 误差最小的能量泛函

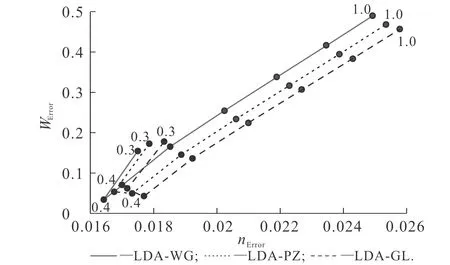
图8 TFvW动能泛函中不同vW动能泛函比重对基态 密度误差及功函数误差的影响Fig. 8 Ground State Density Error and Work Function Error Obtained by Different vW Kinetic Energy Functional Proportions

不同vW动能泛函比重下的基态密度误差与功函数误差计算结果如图8所示.图8中包含了LDA-WG,LDA-PZ和LDA-GL 3种交换关联势,点线旁的数字代表vW动能泛函的比重.例如:LDA-WG交换关联势中,数字1.0代表vW动能泛函的比重为1.0,该点横坐标值为0.024 9,纵坐标值为0.487,分别对应这一能量泛函下的基态密度误差和功函数误差.图8中,vW动能泛函的比重由0.3增加至1.0,相邻点之间的差距为0.1.

对于LDA-WG交换关联势,随着vW动能泛函比重的增加,基态密度误差先减小后增加,由0.017 5(vW动能泛函比重为0.3时)减小至最小值0.016 4(vW动能泛函比重为0.4时),最后上升至0.024 9.使用LDA-PZ和LDA-GL交换关联势计算得到的基态密度误差趋势与LDA-WG交换关联势的基本一致.其中LDA-PZ交换关联势的基态密度误差由0.017 9下降至0.016 8,最后上升至0.025 4;LDA-GL交换关联势的基态密度误差由0.018 3下降至0.017 1,最后上升至0.025 8.3种交换关联势的基态密度误差最小值点均出现在vW动能泛函比重为0.4时.对于功函数,使用3种交换关联势计算得到的功函数误差同样随vW动能泛函比重的增加,呈现出先减小后增加的趋势.使用LDA-WG,LDA-PZ和LDA-GL交换关联势计算得到的功函数误差最小值分别为0.035,0.051,0.043 eV,分别出现在vW动能泛函比重为0.4,0.5,0.5时.当vW动能泛函比重为1时,使用LDA-WG,LDA-PZ和LDA-GL交换关联势计算得到的功函数误差分别上升至0.487,0.467,0.456 eV.

以上结果说明,TFvW动能泛函中,vW动能泛函比重对基态密度误差和功函数误差均有较大的影响.原因主要是,随着vW动能泛函比重增加,OF-DFT计算得到的功函数增加,基态密度的衰减速度降低.此外,尽管交换关联势对功函数有较大影响,比如当vW动能泛函比重为1时,LDA-WG,LDA-GL和LAD-PZ交换关联势的功函数分别为3.538,3.478,3.368 eV,但对于相同的动能泛函,使用3种交换关联势计算得到的功函数误差却相差不大,比如当vW动能泛函比重为1.0时,LDA-WG,LDA-PZ和LDA-GL的功函数误差分别为0.487,0.467,0.456 eV.原因在于,作为参考值的DFT计算结果同样受交换关联势的较大影响.研究结果进一步说明,vW动能泛函比重为0.4的TFvW能够适配不同的LDA交换关联势.

3 结论

本研究以DFT的计算结果作为参考值,计算了OF-DFT在金属板钠体系中获得准确基态密度和功函数所需的能量泛函.在DFT和OF-DFT中,不同交换关联势的使用对基态密度的影响较小,而对功函数有较大影响,这是因为交换关联势主要在远场起作用.此外,OF-DFT中,vW动能泛函比重同时影响基态密度和功函数结果,因此找到合适的vW动能泛函比重至关重要.笔者定义了OF-DFT的基态密度误差与功函数误差,通过数值实验发现,vW动能泛函比重取0.4时,利用不同LDA交换关联势计算得到的结果具有较短高的准确度.值得注意的是,对于功函数,作为参考值的DFT计算结果受到交换关联势的影响,在vW动能泛函比重为0.4时,不同交换关联势的基态密度误差和功函数误差较小,这说明vW动能泛函比重为0.4的TFvW能够适配不同的交换关联势.因此,vW动能泛函比重为0.4时,OF-DFT能给出与DFT较符合的基态性质.OF-DFT无需计算单粒子波函数,计算高效,能应用到更大尺寸的复杂纳米结构中.