三能级原子与光场的动力学演化特性*

2023-12-22 08:18卿嘉阳邬云文

吉首大学学报（自然科学版） 2023年6期

卿嘉阳,邬云文

(吉首大学物理与机电工程学院,湖南吉首 416000)

动力学演化特性是复合系统之间牢不可破的量子相关性,该特性可以揭示系统在各个时刻的状态及不同状态之间的变化规律,是描述物体运动最有趣的现象之一,对量子网络及量子信息起着至关重要的作用[1-2].动力学演化特性对量子计算及量子通信相关领域的发展至关重要,其中光与物质相互作用下的动力学演化特性备受学者的关注[3-4].

在光和物质相互作用的研究中,学者常常将相对较强的泵浦场视为经典场,并忽略其量子特性[5-6].然而,如果想要全面描述光和物质相互作用的量子特性,所有的光场就应该是量子化的[7-9],甚至包括强泵场.Villar等[10]和Coelho等[11]在理论上证明了,标准的三共阈值以上的光学参量振荡器(OPO)会产生泵浦、信号和空转的三方纠缠.旋转波近似中的Jaynes-Cummings模型[12]一直是学者深入研究的主题.最近,学者开始关注原子相干态[13].研究发现,最初处于原子相干状态的JCM与真空场组合可以产生场压缩及原子偶极变量波动的压缩,压缩原子可以辐射压缩光[14-16].一些学者对具有初始相干原子的热Jaynes-Cummings模型中场和原子压缩之间的关系进行了探讨[17-18].此外,学者在理论计算中发现,旋波近似下波函数有解析解,因而在弱耦合及少光子数的情况下,旋波近似是应用最广的近似方法[19-20].

在研究原子和光场的动力学演化特性时,许多学者只考虑了系统的激发概率,而忽略了激发概率与量子态之间的联系.将激发概率与量子态联系起来,对于理解量子力学的基本原理,实现更高效的量子计算都具有重要的意义.笔者拟在特定的初始条件下,运用拉普拉斯方程对三能级原子与光场相互作用系统的量子态进行精确求解,并通过量子态的波函数计算系统的动力学演化特性.

1 模型及方法

图1 三能级原子与光场相互作用系统Fig. 1 Diagram of a Three-Level Atom Coupled with a Light Field

H=ωaa†a+ωcc†c+ωdd†d+g(a†c†d+acd†).

其中:a†表示b1↔b2的产生算符;a表示b1↔b2的湮灭算符;c†表示b2↔b3的产生算符;c表示b2↔b3的湮灭算符;d†表示b3↔b1的产生算符;d表示b3↔b1的湮灭算符;g表示三能级原子与光场的耦合强度.

在考虑2个激发态的情况下,系统的相干叠加态向量

φ=b1|b1+b2|b2+b3|b3.

其中:|b1表示ωa所对应的量子态;|b2表示ωc所对应的量子态;|b3表示ωd所对应的量子态.根据薛定谔方程严格解,不同量子态之间的薛定谔方程可以写为以下偏微分方程:

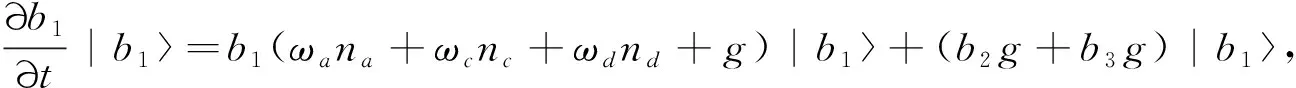
(1)

(2)

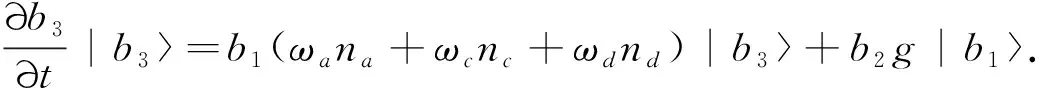
(3)

其中:na表示系统内各能级之间a†a算符的光子数目;nc表示系统内各能级之间c†c算符的光子数目;nd表示系统内各能级之间d†d算符的光子数目.系统的初始条件为b1(0)=1,b2(0)=b3(0)=0.接下来,运用拉普拉斯方程对(1),(2),(3)式进行精确求解,得到

(4)

(5)

(6)

为了系统归一化,对系统作以下变化:

求得归一化系数

将A引入(4),(5),(6)式,可得

2 结果

本研究是在三能级系统下开展的.系统哈密顿量的相互作用主要涉及光场及其对应的能级,由7个变量(g,ωa,ωc,ωd,na,nc和nd)一起控制.计算激发概率发现,通过改变变量之间的耦合系数来进行系统分析,能够清晰地呈现系统激发态变换的物理过程,并充分展现参数如何影响系统的动态行为.原子处于|b1,|b2和|b3态的激发概率随时间演化规律如图2所示.

图2 原子处于|b1,|b2,|b3态的激发概率随时间演化规律(g=1)Fig. 2 Probability Evolution Plot of Excitation of Atom in |b1,|b2 and |b3 State with Time

从图2(a)可知:0 s时,原子完全处于一个未激发状态;约1.50 s时,基态被激发的概率为0;约3.10 s时,原子处于|b1态的激发概率约为0.50;约4.70 s时,原子处于|b1态的激发概率约为0;约6.26 s时,原子处于|b1态的激发概率为1.0.这说明随着时间的延长,|b1态布居值保持周期振荡性变化.

从图2(c)可知:系统所对应的激发态布居值在同一个周期内产生2个峰,第1个峰出现时间约为1.80 s,峰值约为0.83,第2个峰出现时间约为4.40 s,峰值也约为0.83;|b3在第1个峰值之后产生了1个低谷,时间约为3.10 s,低谷值约为0.25.这说明|b3态布居值也随时间的延长保持周期振荡性变化.

为了进一步研究耦合系数对系统布居值的动力学演化特性影响,接下来探讨不同耦合强度系数(g=5或g=10)下,原子处于|b1,|b2和|b3态的激发概率随时间演化规律,结果如图3所示.

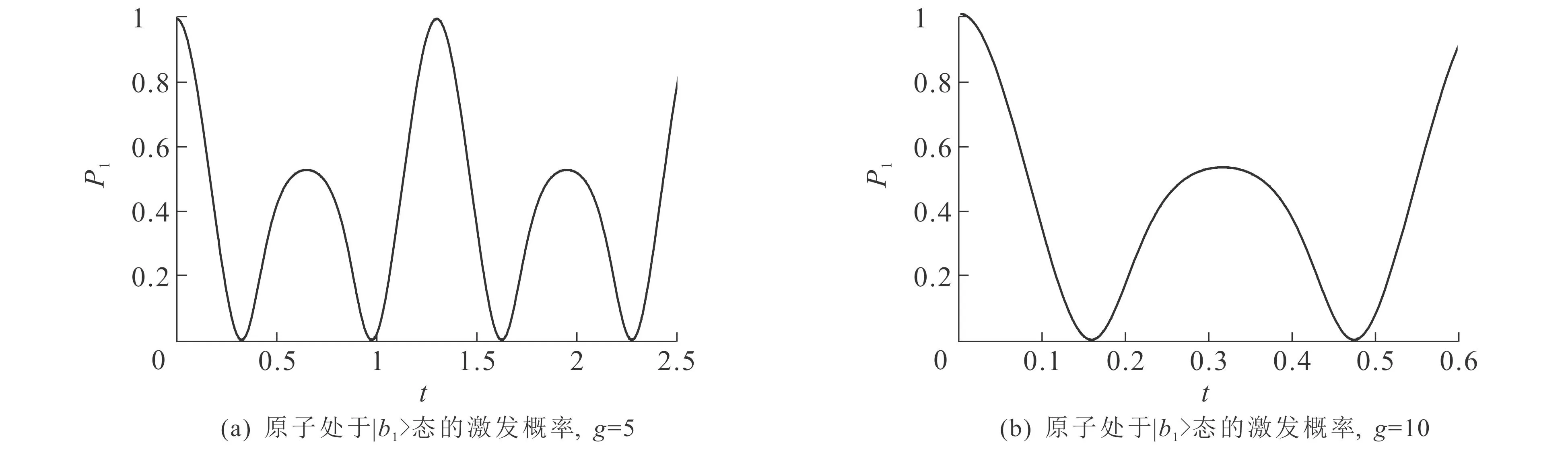
图3 原子处于|b1,|b2,|b3态的激发概率随时间演化规律(g=5或g=10)Fig. 3 Probability Evolution Plot of Excitation of Atom in |b1,|b2 and |b3 State with Time

从图3(a)可知:将系统的耦合系数调至5后,约0.30 s时,基态被激发的概率为0;约0.63 s时,基态被激发的概率为0.50;约1.26 s时,原子处于|b1态的激发概率为1.0.

从图3(b)可知:将系统的耦合系数调至10后,约0.16 s时,原子处于|b1态的激发概率为0;约0.31 s时,原子处于|b1态的激发概率达到峰值,约为0.50;约0.47 s时,原子处于|b1态的激发概率约为0.

从图3(e)可知:将系统的耦合系数调至5后,|b3所对应的激发态布居值在同一个周期内产生2个峰,约0.36 s时产生第1个峰值,峰值约为0.83,约0.88 s时产生第2个峰值,峰值也约为0.83;|b3在第1个峰值之后产生了1个低谷,时间约为0.62 s,低谷值约为0.23.

从图3(f)可知:将系统的耦合系数调至10后,|b3所对应的激发态布居值在同一个周期内产生2个峰,约0.18 s时产生第1个峰值,峰值约为0.83,约0.44 s时产生第2个峰值,峰值也约为0.83;|b3在第1个峰值之后产生了1个低谷,时间约为0.31 s,低谷值约为0.23.

综上,当增大耦合系数时,量子态布居值的峰值大小几乎未变,但每个演化周期内的小振荡明显变多,周期也相应缩短.系统耦合系数的改变导致原子与光场之间量子态的变换速度加快,这也正是原子处于|b1态时,量子态的布居值演化明显变快的原因.本研究证实,通过改变耦合系数可以进一步调控基态和激发态的布居值.

3 结论

笔者探讨了三能级原子与光场相互作用系统的动力学过程,分析了同一耦合强度下不同量子态的动力学随时间的演化特性.结果显示:|b1随着时间的增加,在同一个周期内动力学演化先从1.0减小到0,再从0增加到0.50左右,然后从0.50左右减小到0,最后增加到1.0;|b2随着时间的增加,在同一个周期内出现了3个峰值,系统的动力学演化先从0增加到0.50左右,再从0.50左右减小到0,随后增至0.25左右,再从0.25左右减小为0,然后从0增加到0.50左右,最后从0.50左右减小到0;|b3随着时间的增加,在同一个周期内出现了2个峰值,系统的动力学演化先从0增加到0.83左右,再从0.83左右减小到0.25左右,随后从0.25左右增加到0.83左右,最后从0.83左右减小到0.另外,笔者还分析了不同耦合系数下原子与光场相互作用系统的量子态激发概率随时间演化的特性.结果发现,当增大耦合系数时,系统的振荡特性增强,即系统在每个演化周期内的小振荡明显变多,周期相应缩短.系统的耦合强度对系统的动力学演化特性有很大影响,因而可以通过调节系统的耦合强度来改变系统的动力学演化特性.