节段模型弹簧悬挂颤振试验中的滞回现象研究

李宏杰

【摘    要】：为了研究桥梁颤振运动的非线性特征，进行了平板节段模型弹簧悬挂风洞试验，通过调节系统的机械阻尼比，在不同阶段给予模型外部激励。结果表明：颤振除传统的“软颤振”与“硬颤振”模式外，还有第三种颤振即“颤振滞回”，系统的阻尼是引起“颤振滞回”的主要因素。

【关键词】：风洞试验；非线性颤振；平板节段模型；桥梁；阻尼比

【中图分类号】：U441.3【文献标志码】：A【文章编号】：1008-3197（2023）02-07-05

【DOI编码】：10.3969/j.issn.1008-3197.2023.02.002

Study on Hysteresis Phenomenon in Section Model Spring Suspension Flutter Test

LI Hongjie

（Tianjin Municipal Engineering Design & Research Institute Co. Ltd.，Tianjin 300392，China）

【Abstract】：In order to study the nonlinear characteristics of bridge flutter motion， this paper adopts the method of wind tunnel test of flat section model spring suspension， through adjusting the mechanical damping ratio of the system and giving external excitation to the model at different stages. The results show that in addition to the traditional vibration modes of "soft flutter" and "hard flutter"， there is a third kind of flutter， namely "flutter hysteresis"， the damping of the system is the main factor causing the "flutter hysteresis" phenomenon.

【Key words】：wind tunnel test; nonlinear flutter; plate section model; bridge; damping ratio

桥梁颤振是一种典型的由于气弹不稳定引起的桥梁风致振动响应，具有大振幅且弯扭耦合的特点，一旦出现极有可能导致桥梁损坏甚至坍塌。颤振作为一种具有极大危害性的风致振动是绝对不允许在桥梁上出现的。

目前普遍认知的颤振形式有两种：硬颤振和软颤振。硬颤振是当风速超过颤振临界风速时，主梁发生振动且振动迅速发散直至结构破坏，所以也称为发散颤振；软颤振与硬颤振不同，当风速达到颤振临界风速后，软颤振振动并没有迅速发散，而是出现稳态振幅振动且随着风速增加振幅稳定增大，具有明显的非线性自激振动特征[1～2]，由于其振动相位图呈现出一个稳定的环，故也称为颤振后极限环振动。但在平板节段模型弹簧悬挂颤振试验中，发现了不同于软颤振与硬颤振的第三种颤振状态。

1 平板节段模型弹簧悬挂颤振试验

1.1 试验设置

节段模型弹簧悬挂试验是颤振研究常用的手段，其结构相对简单，方便调节阻尼、质量、刚度等参数；由于是风洞试验，结果较数值模拟更可靠。

试验在精细化风洞中进行，试验段尺寸为500 mm×500 mm×1 050 mm，风机可调风速为0.5～25 m/s，来流湍流度＜0.23%，风场品质良好。见图1。

进行竖向和扭转两自由度节段模型气弹试验，模型发生颤振时，会在竖向与扭转两个自由度上运动。试验框架采用铝型材搭建在不可移动的光学平台上，框架整体刚度良好。节段模型通过弹簧悬挂于风洞试验段内，四壁采用透明有机玻璃板密封覆盖，采用激光位移计实时采集振动数据，以一个光轴及气浮轴套限制节段模型的横向位移，使模型在风洞内仅作竖向与扭转运动。见图2。

1.2 试验工况

由于模型的流线型程度即模型的寬高比、风攻角对颤振有影响，故设置了宽高比8、10、12的3种平板模型及0°、3°、5°、7°、10°5种不同的初始风攻角。不同宽高比模型间采用配重的方式保证具有相同的质量与转动惯量。见表1。

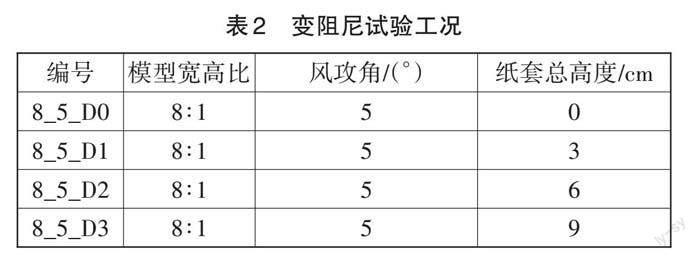
在弹簧上缠绕纸套改变系统的机械阻尼，针对宽高比为8的模型设置了4个不同的纸套高度，用来研究阻尼对矩形断面节段模型发生的颤振行为的影响。见表2和图3。

2 颤振滞回现象

在风洞试验中观察到了典型的软颤振，即当风速超过临界风速后，振动会随着时间发展振幅逐渐增大，但当发展到一定阶段后振动稳定，振幅不再随着时间的增加而增加，将保持一个较为稳定的振幅振动下去。见图4。

对这个软颤振施加初始激励，当施加的初始激励大于其稳定振幅时，振动会在一定时间内从初始激励回到原来的稳定振幅。见图5。

当风速进一步增大后，软颤振也有可能发展为硬颤振。当风攻角较大时，产生颤振滞回现象。不同于典型的软颤振和硬颤振，当达到一定风速后给予一个大的外部激励，振动可以衰减到一个稳定振幅Astable +；当给予一个较小的外部激励时，振动无法发展到Astable +，而是会衰减到一个更小的稳定振幅Astable -，这个Astable -也可能是零。在Astable +与Astable -之间存在一个临界点Acr，当外部激励＞Acr时，振动会随着时间发展到Astable+；当外部激励＜Acr时，振动会衰减到Astable-：这种情况称之为颤振滞回现象。值得说明的是，当风速较低时，Astable-可能为零；随着风速的提高Astable-会增大，Acr也会逐渐减小向Astable-靠近，最后变为软颤振或者硬颤振。见图6。

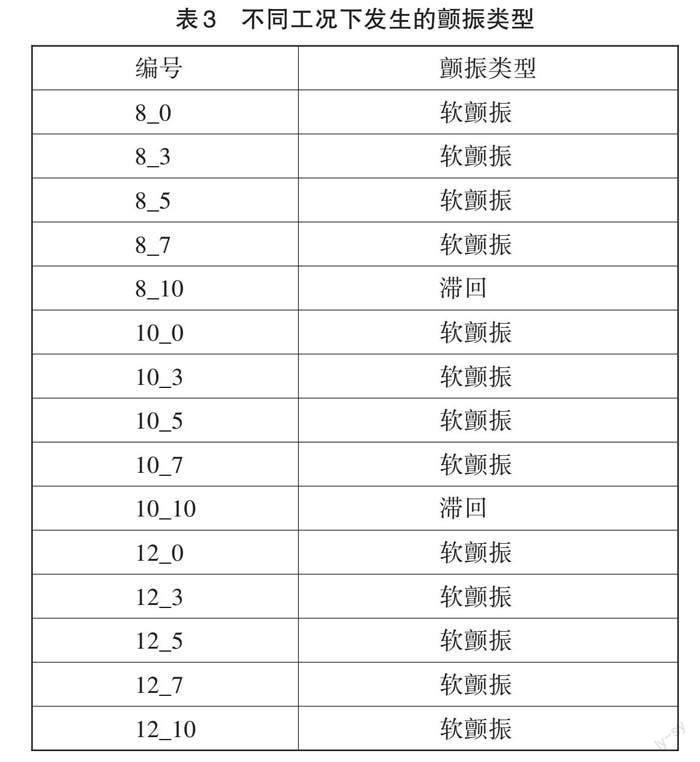
颤振滞回倾向于大攻角和小宽高比的工况。见表3。

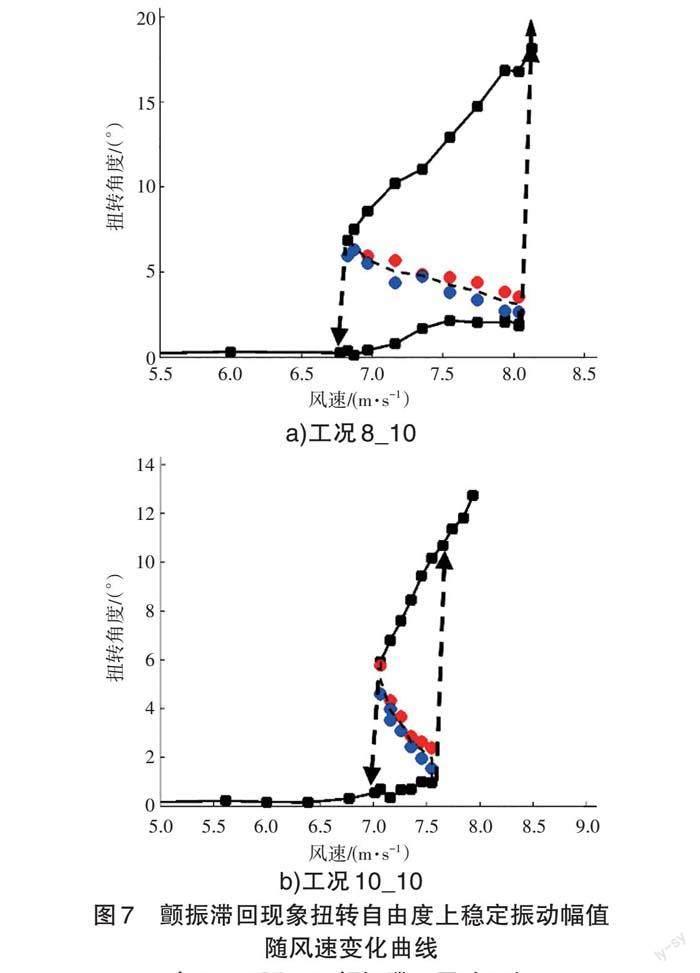
颤振滞回发生时的风速并不是固定值，而是一个风速区间。见图7和表4。图7中上方的黑色实线代表振动幅值的上稳定极限环振幅Astable+随着风速的变化曲线；下方的黑色实线代表振动幅值的下稳定极限环振幅Astable-随着风速的变化曲线；红色点代表试验中振动会上升到上稳定极限环振幅Astable+时所给予的外部激励的大小；蓝色点代表试验中振动会回落到上稳定极限环振幅Astable+时所给予的外部激励的大小；红色点和蓝色点之间的虚线代表的是振动的不稳定极限环振幅Acr随着风速的变化曲线，表明当给予的外部激励位于虚线之下时，振动最后会稳定在下稳定极限环振幅Astable-，当给予的外部激励位于这条虚线之上时，振动最后会稳定在上稳定极限环振幅Astable+；带有箭头的虚线代表振动随着风速的增加或降低，振幅在稳定点Astable+与下稳定极限环振幅Astable-之间的跳跃，当向上的箭头不指向任何点时，即代表振动在下一个风速下发散，不具有稳定的振动幅值。

由图7和表4可以看出：当风攻角相同时，颤振滞回发生的风速区间会随着模型宽高比的增加而减小，颤振滞回结束风速会降低，但是颤振滞回的起始风速值基本没有大改变；表明颤振滞回现象更容易发生于模型宽高比较小、风攻角较大的情况下。

3 阻尼对颤振行为的影响

为了研究阻尼对颤振行为的影响，在弹簧上缠绕不同高度的纸套改变系统总阻尼。选择模型宽高比为8、風攻角为5°的工况进行变阻尼试验，采用等价线性化的方法[3～5]对系统的非线性动力参数进行识别。见图8-图9和表5。

由图8-图9和表5可以看出：在弹簧上缠绕纸套的方式，基本不会影响弹簧的刚度，即系统的自振频率没有发生明显地改变；但很好地实现了对系统阻尼比的改变，随着纸套高度的增加，系统的阻尼比也随之增加且小振幅振动状态阻尼增加的效果十分显著；随着系统阻尼比的提高，颤振临界风速明显提升，说明颤振临界风速与系统阻尼比相关。原本模型在此攻角下发生的是软颤振；但是当增加系统的机械阻尼时，出现颤振滞回且随着阻尼的增加，发生滞回的风速区间明显增大，滞回的起始风速随之提高。

4 结论

通过节段模型风洞试验发现了不同于软颤振与硬颤振的颤振滞回振动模式。当模型的宽高比较小且风攻角较大时，模型发生颤振滞回现象的概率更大，同时比较高的阻尼比会促进颤振滞回现象的出现。

颤振滞回现象的发现丰富了对颤振行为的认知，同时可以看到颤振滞回现象更趋向于发生在阻尼相对较高的、具有钝体气动外形的大跨度桥梁结构上。由于颤振滞回在外部激励下具有一定的突发性，在不大的外部激励下由于颤振滞回现象的发生可能给结构带来较大的振动，故应引起人们的重视。

参考文献：

[1]朱乐东，高广中. 典型桥梁断面软颤振现象及影响因素[J]. 同济大学学报（自然科学版），2015，43（9）：1289-1294+1382.

[2]Chen X，Kareem A. Revisiting multimode coupled bridge flutter：somenew insights[J]. Journal of Engineering Mechanics，2006，132（10）：1115-1123.

[3]陈予恕. 非线性振动[M]. 北京：高等教育出版社，2002.

[4]Rice H J. Identification of weakly non-linear systems using equivalent linearization[J]. Journal of Sound and Vibration，1995，185（3）：473-481.

[5]Gao G，Zhu L. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests[J]. Journal of Sound and Vibration，2015， 355（5）：369-391.