第三方活动冲击荷载作用下近海管道损伤机理及风险评估研究现状

姜逢源，董 胜

（1.中国地质大学（武汉） 海洋学院，湖北 武汉 430074；2.中国海洋大学 工程学院，山东 青岛266404）

油气资源是支撑现代社会生产建设的主要能源［1］。自2017年以来，中国已成为世界第一大石油进口国家，约70%的石油消耗来自于国外进口。为缓解能源消耗压力，减少对外依存度，海洋油气资源开发具有重要战略意义［2］。海洋油气田不论采用何种模式进行开发，都离不开油气输送管道。海底管道作为连接海底设施及陆上终端的介质，承担着输送油气资源的重要任务，其结构安全是保障油气开发生产的关键。

如图1所示，统计资料表明［3-4］，由平台坠物、船舶抛锚等第三方活动引发的冲击荷载是造成管道失效的主要原因。中国有关第三方活动导致管道失效的事故频发，愈加引起工程界关注。2005 年，由于不法分子打孔盗油，导致埕岛油田管道泄漏，对300 km2海域造成污染；2008年，渤西油田天然气管道由于船舶的意外抛锚导致了泄漏；2009 年，埕岛油田由外力拖拽而失效；2011 年，珠海横琴的天然气管道由于机械损伤而发生泄漏事故，导致天然气日产量损失达到4.53×106m3。目前，中国已建设的海底管道以近海管道为主，总长度达6 000 多千米，工作区域多集中在近岸、浅水地区［2，5］。近海管道工作区域内海洋平台、船舶作业等第三方活动频繁，时刻威胁管道输运系统的安全。为有效保护近海管道，使其免受第三方破坏，降低其失效风险，开展冲击荷载作用下海底管道损伤机理及风险评估研究具有重要意义。其目的在于：1）揭示冲击荷载作用下管道损伤与演化机理，明确相关因素对结构响应的作用机制；2）探究含冲击损伤管道失效模式及结构极限承载力，发展管道安全评估方法；3）构建管道风险评估模型，阐明管道失效演变规律，优化管道项目防护策略。最终建立探究结构损伤至失效风险演化规律的完整研究体系，实现近海管道输运系统安全性与经济性的统一。

图1 中国、欧洲北海近海管道失效统计数据及第三方破坏示意Fig.1 Statistical data of failures for offshore pipelines in China and North Sea, and schematic diagram of third-party damages forpipelines

根据上述研究目的，分别从管道损伤机理研究、含冲击损伤管道安全评估研究、管道工程项目风险评估研究3个方面开展国内外研究现状分析，梳理其发展脉络及各部分内容的内在联系，进一步归纳相关研究的关键问题及发展趋势，为中国近海管道安全防护设计及运营维护策略制定提供参考。

1 冲击荷载作用下管道损伤机理研究

1.1 管道损伤失效模式

20世纪70年代起，学者们主要通过物理模型试验的手段探究侧向荷载作用下管道结构响应特征及变形失效模式。Thomas 等［6］通过试验发现，简支条件下，侧向集中荷载作用下管道变形模式分为：局部凹陷，局部凹陷及整体弯曲，结构失效3 个阶段，且其特征与管道几何尺寸密切相关。Ghosh 等［7］通过万能试验机对圆环及短管构件的顶部及底部进行同步加载，获得其管道变形—荷载关系曲线，归纳了不同长径比条件下管道的变形失效模式与损伤特征。针对两端固定管道，Jones 等［8］进行了一系列准静态及动态冲击试验，共130组工况，试验中管径为22～324 mm，冲击位置为管道跨中及四分之一跨长处，试验中总结得到了4种管道失效模式。物理模型试验的开展，为描述管道损伤的半经验模型及理论模型发展奠定了基础。Ellinas 和Walker［9］提出了预测管道局部凹痕深度的半经验公式，在管道变形较小的情况下有较高精度。在此基础上，Bai 和Pedersen［10］基于三维梁柱理论考虑了管道整体变形的影响，对Walker［9］提出的公式进行了修正，其结论适用于管道线弹性区。基于刚塑性理论，Guedes Soares 和Søreide［11］以及Jones 和Shen［12］建立了描述不同边界条件下冲击荷载—管道变形曲线的简化理论分析模型，用于获取管道受撞击后的变形损伤程度。进一步的，基于三维壳体模型，Wierzbicki和Suh［13］建立了考虑轴向荷载及弯矩荷载作用时，管道在侧向冲击作用下的理论分析模型，用于描述管道的局部损伤及变形行为。研究发现，管道变形特征—冲击荷载关系与边界处施加的弯矩荷载及轴向荷载密切相关，且当轴向荷载由预拉力变成预压力时，管道对于侧向冲击荷载的承载力及能量吸收会有明显下降。如式（1）所示，基于Wierzbicki 和Suh 的研究成果，DNV-RP-F107 规范［14］给出了描述管道凹痕深度和冲击能量的公式，其假设冲击荷载全部由管道变形吸收，且忽略了内压的影响，对于管道损伤的评估结果偏于保守。

式中：E为坠物的冲击能量，D为管道直径；t为管道壁厚，mp= 1/4·（σy·t2）为塑性弯矩，σy为管道钢材料屈服强度，δ为管道凹痕深度。

从上述分析可知，冲击荷载作用下管状构件的损伤包含局部凹陷及整体弯曲等多种失效模式。对于真实条件下绵延数公里的海底管道，平台坠物、船舶抛锚等荷载的作用区域远小于管道跨长，同时由于海床土体的连续支撑作用，管道所受冲击损伤以局部凹陷为主。国内外相关研究也集中在探究冲击荷载作用下海底管道的凹陷变形响应［15-18］，并以此作为度量管道损伤的主要依据［14］。Jiang等［19］在实验室条件下开展了坠物—管道撞击试验，受撞击损伤的管道试样如图2 所示。图2 中虚线描绘出了撞击中心处的管道变形横截面，呈“桃”形。管道的凹陷程度在撞击中心处最大，并向两端逐渐减小，随着距离的增加，管道的横截面逐渐趋向于圆形，表明该区域管道结构几乎未受到损伤。凹陷是管道运行中常见的几何缺陷，是由于管壁内凹形成的永久塑性变形。凹陷的存在会引发管道的应变及应力集中，直接影响结构剩余强度，易在压力荷载下引发爆破、疲劳，以及屈曲失效［20-21］。进一步的，为量化管道凹陷程度，Cosham 和Hopkins［18］对管道凹陷深度给出了明确定义：如图3所示，管道横截面直径的最大减少量（AB两点之间的距离）为凹陷深度δ。

图2 管道试件空间变形特征Fig.2 Spatial deformation characteristics for pipeline specimen

图3 管道局部凹陷示意Fig.3 Schematic diagram of pipeline dent

1.2 管土耦合作用下结构响应

为模拟接近真实工况下海底管道的结构响应，更多因素逐渐被考虑在内，包括内压荷载［22］，边界条件［17］，悬跨支撑［16］，轴向预荷载［23］，材料应变率效应［24］等，其中管土耦合作用近年来备受关注［15，17，25-26］。海床土体作为支撑海底管道的连续性柔体，在冲击荷载的作用下通过管土耦合作用，对冲击能量的转化、管道的局部及整体结构响应等方面具有明显影响；同时对于埋置管道，管道上覆土体提供的抗冲击承载力可有效保护管道。上述过程涉及复杂的管土接触模式、土体失效机理及弹塑性行为，在以往分析中并未得到充分考虑。理论模型通常基于某些简化假设，应用范围有一定限制性，对于众多因素叠加下的结构响应描述不再适用。随着计算机运算能力的提高，有限元数值模拟逐渐成为研究管道结构响应特征的主要手段，其具有严谨的理论支撑，在描述管道及土体等固体材料的非线性行为方面具有显著优势，有利于分析管土耦合作用对管道结构响应的影响。对于裸置在海床表面的管道，学者们通过试验及有限元模拟［17，25-26］，建立了坠物—管道—土体模型，探究了刚性海床以及土质海床条件下，管道受撞击时能量转化的差异。结果表明，由于海床土体的柔性，部分冲击能量转化为管道的整体变形及土体的塑性变形，减缓了管道的局部损伤。进一步的，为充分保护管道免受第三方活动带来的冲击损伤，行业规范中指出需要对管道进行挖沟埋深处理［27］。但目前，尚无确定管道安全埋深的明确指导原则［28］。DNV-RP-F107［14］中仅考虑碎石垫层对能量的吸收作用，对埋深并未说明。美国船级社的规范［29］和国际标准化组织的ISO 15649 附则［30］也仅给出埋深的建议值，对于确定原则并未进一步说明；巴西、澳大利亚等国家对此提出的标准也并不全面。中国2021年颁布的《海底管道系统规范》［31］中给出了近海管道的埋深不宜低于1.5～2.0 m，但未给出具体确定依据。许多专家学者对于管道安全埋深做了相关研究。Gao 等［32］和Han 等［33］基于大变形有限元分析技术，考虑土体应变率效应，探究了坠锚在黏土海床中的贯入深度，并拟合相应的预测公式用于确定管道的安全埋深。在此基础上，Jiang等［19，34-36］基于模型试验及数值模拟针对埋置海底管道受坠物的冲击损伤进行了一系列分析，包括损伤机理分析、失效风险分析及经济评估，初步揭示了管土耦合作用对于结构响应的作用机制，阐明了埋深—管道损伤—失效概率的定量关系。图4 阐述了冲击过程中坠物—海床土体—管道结构的相互作用机理（其中，Uv、Uh分别代表管道横截面节点坐标的竖直与水平分量）。在坠物与管道发生撞击作用前，坠物首先会侵入管道上覆土体，冲击作用使得土体逐渐向四周流动，使土体海床表面出现隆起。随着坠物的持续侵入，土体产生较大变形及塑性应变，并逐渐达到剪切破坏极限状态［32］。上述过程消耗了部分冲击能量［17，26］。随后，坠物以衰减后的初速度与管道发生撞击，在该局部冲击荷载作用下管道表面产生明显的凹陷变形，同时由于四周土体的支撑作用，部分冲击能量通过管土相互作用转移到土体中，使得周围土体产生部分位移及塑性应变。随着管道变形程度及土体应变的增加，坠物冲击能量向管道及土体中转移，速度逐渐衰减至零，坠物开始回弹。随后，管道变形弹性部分逐渐恢复，剩余不可恢复的塑性部分趋于稳定。

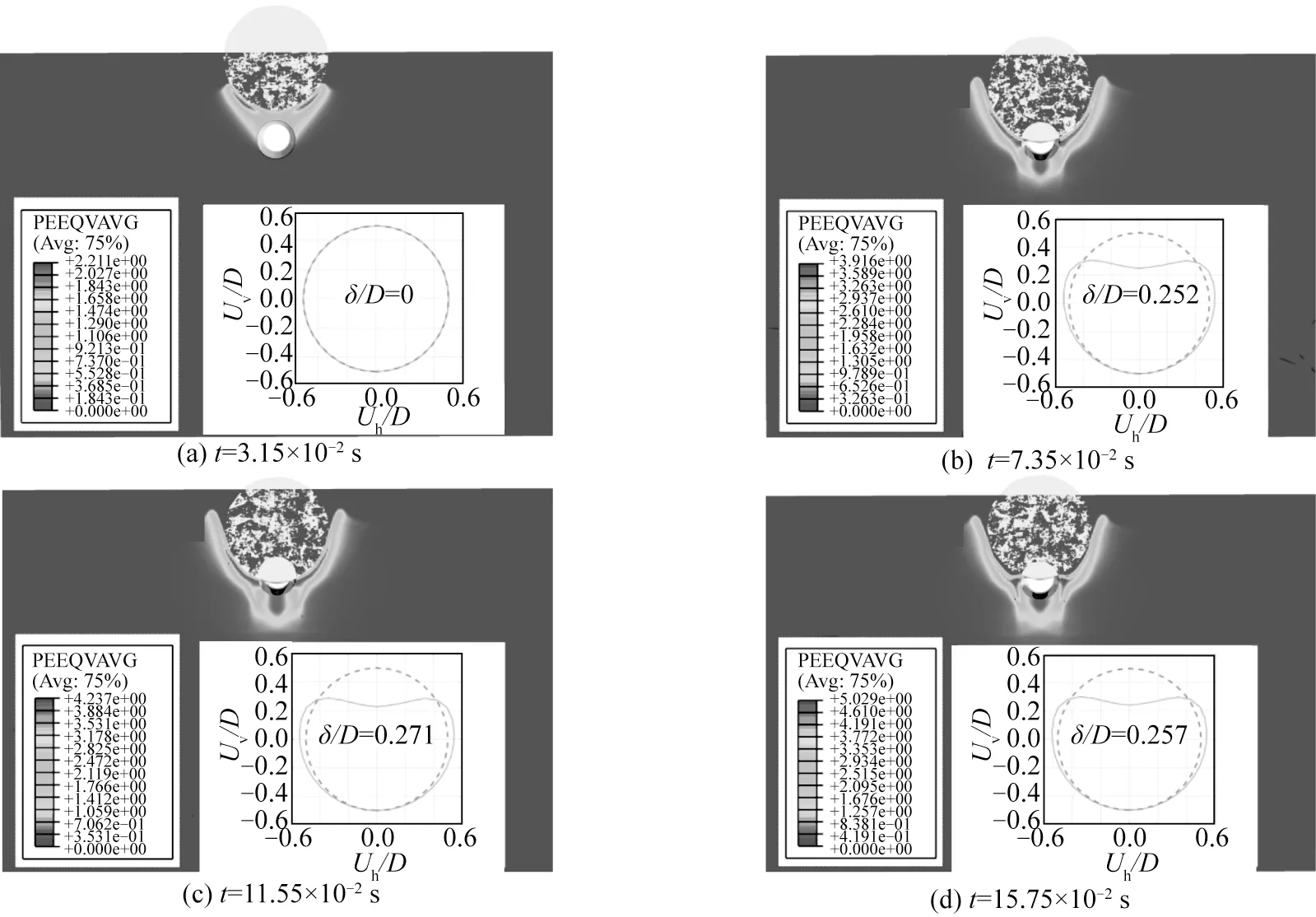
图4 坠物—海床土体—管道结构的相互作用机理Fig.4 Interaction mechanism for dropped object-seabed soil-pipeline during impact process

以上研究表明，管土耦合作用对管道在冲击荷载下的结构响应特征有显著影响，对管道进行挖沟掩埋施工为保护管道免受第三方破坏的有效手段，管道上覆土体受坠物侵入过程中会发生剪切失效，吸收部分冲击能量，减缓管道损伤，土体强度是决定埋深保护效果的关键因素。然而，《中国工程地质学》［37］中指出，由于风浪流、应力条件、沉积条件等多因素复杂作用，海底土层材料性质多变，土体强度具有明显空间变异性特征［37-38］（图5）。在海洋岩土力学研究中发现，土体强度空间变异性直接影响土体的失效机理，明显降低其承载力［38-39］。目前，对于埋深管道冲击损伤分析，大多数研究中均简化海床为均质土体，忽略其强度变异性，无法真实反映土体失效模式及管道结构响应，低估管道损伤程度，为安全设计带来潜在风险。因而如何有效描述土体强度空间变异性，揭示该条件下土体失效模式及管土耦合作用对管道损伤的作用机制为亟待研究的问题。

2 含冲击损伤管道安全评估研究

如上文所述，遭受冲击荷载后管道主要损伤形式为局部凹陷。凹陷的存在会引发应力及应变集中，降低管道结构承载力，继而引发失效事故。如何评估含凹陷管道的安全性，探究凹陷对结构承载能力及失效行为的影响规律具有重要意义。一般情况下，凹陷根据几何特征可分为平滑凹陷和弯折凹陷两类［20］：平滑凹陷不存在壁厚减少，其变形区域中管壁曲率变化较为平缓，凹陷区应变较小；与之相反，弯折凹陷变形区域的管壁曲率变化梯度较大，凹陷区应变较大。但目前关于区分上述两种凹陷类型的临界曲率定义尚未有统一说法［40］。欧洲管道研究中心［41］认为凹陷区域最尖锐部分的曲率半径小于5 倍管道壁厚时，可定义为弯折凹陷。

对于含单纯凹陷（无划痕、沟槽、腐蚀缺陷等复合凹陷）的管道，其安全评估一般通过基于深度或基于应变的评价准则来实现。在此基础上，还应考虑凹陷管道的结构失效模式及极限承载力，以全面评估其安全状态。尤其是对于弯折凹陷的情况，其应力集中更为严重，失效包含高塑性应变等复杂力学行为，需进一步展开研究。

2.1 基于深度的评价准则

对于含凹陷管道的安全性评估，由于测量数据容易获得，基于深度的评价准则应用最为广泛。挪威船级社在规范DNV-RP-F101［14］中给出了不同凹痕深度与管道外径比值δ/D下对应的损伤分级标准，如表1 所示，可以看出，当δ/D超过5%时管道即存在泄露风险。加拿大标准协会在规范CSA-Z662-16［42］中指出，当凹陷最大深度超过6%外径时，需采取修复操作。此外，在诸多国外规范中，如ASME B31.8［43］、API 579-1/ASME FFS-1［44］、PDAM［45］、API PUBL 1156［46］、DOT 49 CFR 192［47］中也给出了类似的临界深度标准，其取值在2%～10%外径之间，大多数为6%外径。中国国家能源局在规范SY/T 6996—2014 也将6%外径作为临界凹陷深度标准［48］。

表1 管道损伤分级标准Tab.1 Damage classification of steel pipelines

然而相关研究表明［49-50］，单纯以凹陷深度评估结构的安全性难以真实反映结构的应力应变状态，还应考虑凹陷长度、凹陷宽度的影响。Baker［49］研究了不同尺寸凹陷的应力分布特征发现，凹陷深度相同时，长凹陷的最大应力要大于短凹陷的最大应力。Rosenfeld［50］开展了含不同尺寸凹陷管道的疲劳试验，发现狭长凹陷的失效区域（最大应力应变区域）位于凹陷中心处，而短宽凹陷的失效区域位于凹陷边缘。随着管线用钢等级的提高，材料韧性不断增强，基于深度的评价准则过于保守。此外，即使在凹痕深度较小的情况下，管道也存在疲劳失效的可能［51］。

2.2 基于应变的评价准则

随着管道缺陷检测装备与技术的发展，可获取管道凹陷区域的高精度内检测数据，基于应变的评价标准应运而生：根据凹陷区域的离散测量数据，通过插值或拟合等数值方法［52-53］，建立描述凹陷曲面几何特征的函数，进而估计凹陷处的应变，以此作为评估结构安全性的指标。相较于基于深度的评价准则，基于应变的评价准则描述了结构在极限状态下的应变特征，可反映客观物理规律，一般认为具有更高精度。2007年，美国船级社在规范ASME B31.8［43］中提出了相应的基于应变的评估准则，其假设应变最大区域位于凹陷最深处，基于平面应变条件给出了关于环向弯曲应变εcb、轴向弯曲应变εlb、轴向薄膜应变εlm的解析表达式（式（2）～（3）），进一步按式（4）～（5）估计凹陷处的最大等效应变εmax。计算图示见图6［43］。该准则指出，当最大等效应变达到εmax=εc= 6%时，需采取修复或更换措施。其临界值εc= 6%为3%～12%之间选取的数值，3%为规范ASME B31.4［54］及ASME B31.8中所允许的弯曲极限应变，12%为管材应变极限［49］，在这一应变状态下材料变形开裂的可能性会增加。该方法为基于应变的评价准则建立了基本分析流程，为后续相关研究奠定了基础。Gao 等［55］通过研究发现，环向薄膜应变及剪切应变对于应变的评估结果有重要影响，而ASME B31.8准则中未考虑上述因素的贡献，存在一定局限性。进一步的，Lukasiewicz 等［56］提出了一种凹陷应变分析程序，在由凹陷处曲率估计弯曲应变的基础上，结合理论解析及壳单元有限元模型对轴向及环向薄膜应变进行了求解，同时考虑了切应变的影响，基于塑性应变理论给出了等效应变的评估结果。其精度高于ASME B31.8 准则，然而需要注意的是，该方法需依托于管道凹陷区域的高精度内检测数据以及有限元模拟，在涉及大变形问题时易产生计算问题，应用范围受到限制。为实现管道应变的快速评估，Okoloekwe 等［57］提出了一种解析方法，将管道凹陷区域的变形分解至轴向、径向及周向3 个方向，基于B 类样条曲线建立相应的曲率特征函数，通过对上述函数的微分得到管道凹陷区域的应变张量。相较于ASME B31.8准则，该方法可描述非平面应变条件下的应力状态。然而由于未考虑初始缺陷、应力集中等因素的影响，评估结果相较非线性有限元分析结果偏为保守。

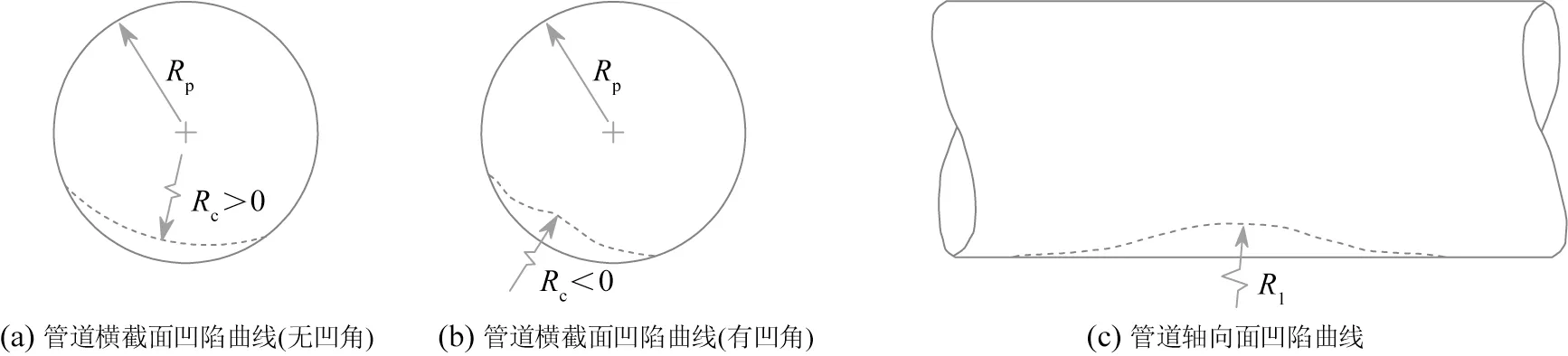
图6 ASME B31.8应变评估准则计算图示Fig.6 Schematic diagram of strain-based assessment criterion in ASME B31.8

上述研究表明，对于含单纯凹陷的管道，理论解析法和有限元分析法均可以较为合理地评估管道缺陷区域的应力状态，从而判断结构的安全性。理论解析法通常基于某些简化假设条件，评估精度较低，但计算效率较高。有限元分析法可宏观考虑多种因素的影响，评估结果更为精确，但需要依托专业知识，同时对计算资源的需求较大。实际应用时，可基于解析法快速判断凹陷的严重程度，继而对目标工况采取有限元分析，以细致观察其结构应力应变状态［57］。

式中：εcb、εlb、εlm分别为环向弯曲应变、轴向弯曲应变、轴向薄膜应变；x，y分别为管道横截面节点的横、纵坐标；εin、εout分别为内、外表面等效应变；Rp为管道半径；Rc、Rl分别为管道横截面、轴向面曲率半径；d为凹陷深度；L为凹陷长度。

2.3 内压荷载下结构响应特征

如前所述，凹陷的存在会引发应力应变集中现象，直接影响结构承载能力。研究发现，一些案例中凹陷即使满足基于深度或应变的评价准则，管道仍会发生失效［51，58-60］。因此，对于含凹陷管道的安全性评估，在根据凹陷区变形尺寸以基于深度或基于应变的准则判断其安全性的基础上，还应对其结构承载力进行校核。对于近海管道而言，内压荷载为首要考虑的外部荷载［40］。探究含凹陷管道在内压荷载下的结构响应特征，明确相应承载能力，对准确判断结构安全状态具有重要意义。

当凹陷种类为平滑凹陷时，其不存在壁厚减少，凹陷形成过程中材料会产生应变硬化效应，使其材料强度提高，同时内压荷载作用下凹陷发生回弹，一定程度上减缓了缺陷形变，其剩余强度未有明显下降［40，60-61］。而对于弯折凹陷，情况则有所不同。Jandu 等［58］通过有限元分析发现，含有曲折凹陷的管道，其剩余强度较无缺陷管道有显著降低，并指出由于未考虑凹陷区域曲率的影响，美国石油协会规范API-579-1/ASME FFS-1［44］中基于深度的评估准则不再适用于含曲折凹陷管道的安全性评估。为进一步探究凹陷对管道爆破压力的影响，刘啸奔等［62］通过非线性有限元模拟，分析了管道爆破压力与凹陷深度、凹陷半径、径厚比的关系，并拟合了相应的经验公式。研究发现，随着凹陷深度的增加、凹陷半径的减小，管道的爆破压力呈明显的下降趋势。田骁［60］基于等效塑性应变失效准则［63］，探究了凹陷深度、曲率对于管道极限压力的影响规律，确定了相应的临界曲率半径及临界凹陷深度，修正了基于深度的评价准则。此外，凹陷对内压荷载下管道的应变分布特征有明显影响，继而对失效模式及承载力产生作用。针对API 5L X52管道，Shuai等［64］通过原尺度管道压力试验（管径为D=720 mm，壁厚为t= 8.1 mm）及有限元分析发现，在内压荷载加载过程中，凹陷区域的应变变化频繁，且凹陷中心处的应变变化量最大。这一特征表明，工作内压的微小波动有可能引发管道应变的剧烈变化，在长期工作状态下易引发结构的疲劳失效。Huang和Zhang［65］基于非线性有限元分析探究了内压荷载下含凹陷的API 5L X80 管道的塑性应变分布规律。研究发现，随凹陷深度变化，塑性应变最大的区域逐渐由凹陷深度中心沿着周向往边缘偏移，且凹陷曲率变小时，塑性应变不断增大，有可能产生爆破失效。而ASME 规范中假定最大塑性位置出现在凹陷中心的条件不符合上述结构响应特征，此时基于应变的评价准则是否适用有待进一步研究。同时，研究指出管道壁厚对于塑性应变分布也有重要影响。

Zhang 等［40］指出，目前对于含弯折凹陷的管道，相关的压力试验及数值分析研究成果较少，内压荷载下结构响应特征尚不清楚，难以准确描述凹陷特征对管道承载能力（剩余强度、疲劳强度）的影响规律。若采用基于深度或基于应变的准则来评估结构安全性，易产生较大偏差。由于海洋环境荷载以及人类第三方活动的强随机性特征，平台坠物、船舶抛锚等冲击荷载作用于管道的位置、角度、量级等因素多变。冲击荷载对管道产生凹陷损伤的种类、位置包含多种情况，对管道结构响应的影响规律也不尽相同。因此，如何将凹陷特征对结构失效特征及承载力的影响融入管道安全评估方法中有待进一步研究。

3 管道工程项目风险评估研究

为保障海底管道系统安全运行，优化管道项目运营经济效益，实现管道工程项目安全性和经济性统一，需开展两部分研究工作：1）定量风险评估，准确识别管道失效概率；2）经济风险评估，基于定量风险评估，同时考虑管道失效的经济成本后果，以及管道建设防护的投入成本，形成合理完善的管道建设、检修及维护策略。

3.1 定量风险评估

定量风险评估是减小海底管道失效概率、降低事故后果的有效途径。Moan等［66］给出了平台附近船舶撞击及坠物落水的概率计算方法及对应的能量大小，并对其进行了风险评估。Katteland和Oeygarden［67］针对深水落物的风险进行了分析，给出了不同类型坠物的荷载分布。Bai和Bai［68］给出了各种类型撞击下海底管道的失效概率，研究了其风险的预测及可接受准则。Mazzola［69］提出了一种估计海底管道受平台坠物撞击的失效概率方法，该方法以凹陷深度大于20%管径作为失效的判据，分析了不同坠落点、管道地点对失效概率的影响，并将该方法应用到两个工程案例中。基于类似的原理，挪威船级社在DNV-RP-F107 规范［14］中提出了坠物撞击下海底管道失效概率的计算方法：首先计算坠物击中管道的概率；随后估计管道在撞击事故发生时的失效概率，二者的乘积即为管道总失效概率。该方法为后续研究提供了良好的分析框架。在此基础上，许多专家学者对管道的碰撞及失效进行了评估。丁红岩等［70］改进了DNV规范方法中碰撞概率的估计方法，求解不同坠物撞击下管道的失效概率，并指出坠物质量及管道尺寸是影响失效概率的主要原因。但上述方法大多数采用经验公式描述管道损伤程度，忽略了冲击过程中非线性因素的影响。为解决上述问题，Kawsar等［71］结合有限元分析及蒙特卡洛抽样法得到了管道失效的超越概率，并充分考虑管道受冲击荷载下的结构非线性因素，评估结果更精确。Jiang 和Dong［34-35］进一步考虑管土耦合作用及管道埋深的影响，结合概率抽样、有限元分析及机器学习算法，建立了管道失效概率与管道埋深及土体性质之间的定量关系，为管道安全埋深确定提供参考。

对于管道受撞击损伤的失效风险评估，其结构极限状态方程一般可按式（6）表示。其认为当变形凹陷深度与管径比值δ/D达到某一临界值时，管道即发生失效，而ηc的取值则对应着不同的风险接受准则，ηc取值越小，对应风险接受准则越为严格。DNV 规范［14］指出，当δ/D仅超过0.05 时，将不会对管道结构产生实时影响，但需要对其进行检查和功能评估。当δ/D超过20%，此时管道会发生破裂，会立即威胁到人类的生命，并对经济和环境带来重大损失。Jiang和Dong［34］在其研究中曾探讨过这一问题，图7给出了不同风险接受准则下管道结构累积失效概率Pcf与埋深e的关系。当ηc=0.05 时，即使埋深e=2.0 m 的管道也无法保证其累积失效概率Pcf＜ 1×10-5。相比之下，当ηc=0.20时，埋深为e=1.0 m时管道结构的累积失效概率即可满足Pcf＜ 1×10-5，其具体数值大约是ηc=0.05准则下相应失效概率的四分之一。可以看出，不同失效判别标准下对应的失效概率与安全埋深有明显差异。因而，选取合适的管道失效评估准则为失效风险评估的关键因素。

图7 不同风险接受准则下管道累积失效概率随埋深的变化Fig.7 Variations of pipeline cumulative failure probabilities with burial depth subjected to different risk acceptance criterions

式中：x为随机变量矢量；ηc为管道失效临界参数，根据风险接受准则而定，一般可取ηc=0.05～0.20。

3.2 经济风险评估

在管道项目设计及运营阶段，常采取挖沟埋深以及定期检修维护等手段，以降低冲击及腐蚀引发的失效风险。然而，过度保护措施势必引起投资的巨大增加，反之，若保护措施不足，则引发严重经济损失和环境污染。因此，需充分考虑事故发生的失效概率、经济成本后果（如管道事故产生的经济损失费、环境损失费等）及投资成本［72］，对管道项目进行经济风险评估，从而采取恰当防护手段，保障管道项目安全性及经济收益。

Park 等［73］开发了一种管道运营风险管理系统，用于评估管道失效概率及相应的后果成本，归纳总结了引起管道失效的主要原因，包括第三方破坏、腐蚀、焊接缺陷及地层运动。Shafiee 和Ayudiani［74］提出了一种基于风险的管道工程完整性评估模型，采用贝叶斯理论计算腐蚀因素影响下海底管道的失效概率，结合相应后果成本及投资成本（设备检查、维护和修理等费用），得到项目运营最优策略。类似的，Tee 等［75］建立了管道全周期成本优化模型，首先分析了管道服役期内在腐蚀和外界荷载等因素下的失效概率，继而考虑风险及成本因素，通过智能算法寻找最佳管道维护方案。Aljaroudi 等［76］针对海底原油管道，考虑管道腐蚀泄漏失效及泄漏检测装置失效的联合概率，建立了基于时变可靠度理论的经济评估模型，给出获得预期运营收益的临界干预年份。

目前，相关研究中的经济风险评估大多是针对腐蚀管道开展的。通常是对项目进行期望理论分析，如式（7）所示，根据期望生命周期成本Lcc（life cycle cost，简称LCC）的货币价值来进行决策。一般情况下，最佳方案为使Lcc的货币价值达到最小的方案（式（8））。在上述研究中，第三方破坏往往仅作为引发风险的一个因素被考虑在内，因而难以针对性评估相关防护措施对应的失效概率及经济收益。同时，第三方破坏属于典型的低概率—后果严重事件（失效概率量级在10-5～10-3左右），类似于建筑结构中的地震灾害［77-78］。此时若继续采用期望理论进行分析，所估计的期望经济损失值会因过小的失效概率而导致最终的结果微乎其微（式（7）等号右边第三项），此时采取防护手段获得的防护收益甚至为负值，这一现象及结论也在关于建筑结构抗震经济分析及船舶综合安全评估的研究文献中得到了印证［79-80］。针对这一特征，学者们建议通过引入效用理论［81-82］及累积前景理论（cumulative prospect theory，简称CPT）［83］来评估低概率—后果严重事件的经济风险。CPT 引入了价值函数和权函数的概念来评价失效事件的后果及相应的失效概率，通过调节低概率—后果严重事件及高概率—后果轻微事件的权重，使决策更符合客观规律，能解释人们在选择决策偏好的非线性、追求风险和规避损失等现象。基于累积前景理论及定量风险分析模型［34］，Jiang 和Dong［36］建立了管道第三方破坏防护项目的经济评估模型，得到了管道埋深、失效概率及防护收益三者间的定量关系。

式中：Lcc(T)为管道项目生命周期成本；T为管道服役周期；E（·）为求期望函数；Cini为项目初始投资；CM（i）为第i年的维护费用；Cf（i）为第i年因失效事故引起的经济损失；Pf（i）为第i年的失效概率；Lcc，opt为最优管道生命周期成本；Lcc，j(T)为第j个决策方案对应的管道项目生命周期成本；n为决策方案的个数。

总体上看，关于管道风险评估研究的相关理论及方法较为完善，为后续研究提供了可靠的分析模板。然而需要注意的是，目前海底管道第三方破坏的风险评估研究中大多数以基于深度的评估准则作为受冲击损伤管道的失效判据。相关研究中指出，失效判据对于风险评估的结果有重要影响。因而在后续风险评估研究中，应着重考虑凹陷特征对结构失效模式及承载力的影响：针对潜在的多种凹陷损伤特征，将相应的安全评价准则纳入失效判据体系中。

4 结论与展望

近海管道为中国海洋油气开发产业的重要组成部分，其安全性问题至关重要。第三方活动引起的冲击损伤是近海管道失效主要原因。随着海洋资源开发强度的逐年增加，人类第三方海洋活动越发频繁，势必增加管道失效风险，对管道安全设计及防护策略提出新的挑战。文中围绕冲击荷载作用下管道损伤机理及风险评估这一主题，针对其损伤机理、安全评估及风险评估3 个方面的国内外研究现状进行了综述，梳理了各部分研究内容的发展脉络及各部分内容间的承接关系，明确了影响管道安全的关键因素，并对未来的研究工作提出建议。

1）忽略海床土体的理想条件下，管道在冲击荷载作用下的损伤机理研究已有较为丰富的成果，相应的模型试验及理论模型可以较好描述管道变形与冲击荷载的定量关系。进一步考虑管土耦合作用时，由于其涉及诸多包括土体大变形、材料应变率效应等复杂因素，非线性有限元分析结合试验验证为主要研究手段。管土耦合作用对于管道结构响应有重要影响，管道上覆土体受坠物侵入过程中会发生剪切失效，吸收部分冲击能量，减缓管道损伤，土体强度是决定管道损伤程度的关键因素。然而海床土体性质多变，强度具有明显空间变异性特征。相关研究指出，在强度空间变异性条件下，土体具有多种失效模式，承载力较均质土体明显下降。若忽略这一因素，会低估管道损伤程度。因此，在未来研究中应重点探究强度空间变异性条件下管道上覆土体的失效模式及管道结构响应特征。

2）局部凹陷为冲击荷载对管道造成损伤的主要形式，包含平滑凹陷及弯折凹陷。对于含凹陷管道安全评估，目前大多数方法均以基于深度或基于应变的评价准则开展。对于平滑凹陷，上述方法具有较高精度。对于弯折凹陷，凹陷区域曲率变化梯度较大，应力应变集中更为严重，其剩余强度及疲劳强度明显下降，上述评价准则不再适用。目前相关研究较少，包括内压荷载下凹陷特征对结构失效行为的作用机制，对结构承载能力影响规律，以及弯折凹陷的临近曲率定义等。

3）对于冲击荷载作用下海底管道工程项目的失效风险及经济风险评估，相关研究方法与体系较为成熟。为考虑结构损伤的非线性因素，可采用有限元模拟、蒙特卡洛抽样及机器学习算法结合的手段实现数值分析与概率分析的耦合问题。对于管道第三方破坏这类低概率—高风险事件，建议采用CPT 理论进行经济风险评估，可合理平衡失效概率及后果的权重。但目前大多数研究中对于失效准则的判断均来自于基于深度的评估准则，这种方法对于弯折凹陷的情况会引起较大误差，影响失效概率估计精度及防护策略制定。概率分析中，不同抽样工况中管道凹陷损伤特征多变。因而在今后研究中应考虑不同凹陷特征对结构失效行为的影响规律，基于相应凹陷安全评估准则构建全面的失效判据体系，以合理估计具有凹陷损伤多样性特征的目标管道失效概率。