基于改进AHP-GRA理论的风叶更换最优方案探讨

何青，黄久强，何亚，吴凡，郑福鹏

（1.中国电建集团华东勘测设计研究院有限公司，杭州 311122；2.重庆大学，重庆 401331；3.中国矿产资源集团舟山发展有限公司，浙江 舟山 316000）

1 引言

风电工程是新能源发展的重要组成部分，将绿色进行到底的风中舞者在全球各地相继现身。美国能源部发布了到2050 年海上风机从4.2 万kW 到11 000 万kW 装机容量的战略计划；欧洲风能协会2021 年报告中也提到了期望在2022—2026 年新增装机容量达到27.9 GW 的规模；履行大国使命，推动发展绿色能源[1]，在国内更是有风、光电在2030 年达到12 亿kW 总装机容量的宏伟蓝图。

未来风电工程规模庞大，风机叶片作为脆弱的部件，在运输、安装等过程中容易受到各种不利因素的影响而出现缺陷或损伤，再加上风机高耸，极易遭受雷电的袭击，无论是安装或投运过程中损坏，都将导致非常规的修复或拆换设备的情况。作为具有一定危险性的施工方案，若能够将“经济、技术、安全”3 项指标纳入评价体系，既能降低成本，确保技术可靠，又能大大增加未来施工的安全保障。

2 引入AHP-GRA理论，构建评价模型

构建“目标-准则-指标”的理论模型。对准则层，指标层的因子进行两两比较，将传统九级标度简化为更具区分度的五级标度，如表1 所示。

表1 两类标度方法

2.1 建立指标因子集特征矩阵

构建n 个可选方案的集合X={X1，X2，…，Xn}T，设Xi={xi1，xi2，…，xim}为方案i 的m 个指标因子，且集合中存在Xj={xi1，xi2，…，xij}表示为方案i 的第j 个指标因子。若存在一个理想方案X0={x01，x02，…，x0m}是来自各个方案{X1}，{X2}，…，{Xn}的最佳因子，可得n+1 个方案指标因子集的集合X'={X0，X1，X2，…，Xn}T[2]。

2.2 指标特征矩阵的归一化

各因子进行无量纲处理，将数据映射到[0，1]的区间。若因子类别数值越小越好，如成本开销，则记为I1；若因子类别数值越大越好，如技术可靠度，则记为I2[3]，显然I1，I2∈{1，2，…，m}，令：

式中，xij是指标矩阵（1）中第i 个方案的第j 个指标的原始值。式（1）中，显然Dij∈[0，1]，当Dij越接近于1，说明该方案指标越优。于是，可得归一化后的无量纲矩阵[4]：

2.3 构建灰色关联系数矩阵

引入灰色关联系数公式，用于评判各指标因子的关联程度，比较指标集合{Di}={(di1，di2，…，dim)}（i=1，2，…，n）。取归一化处理后矩阵Di中各元素，引入式（3）灰色关联系数：

2.4 由指标权重建立综合评判矩阵

对比选方案各指标的优劣排序判别[5]，采用指数标度法赋值，确定权重，得到n 阶矩阵An，求出特征值λmax与特征向量W=（w1，w2，…，wn）T，并进行一致性检验，其中平均随机一致性指标可查平均随机一致性指标。

将上述特征向量（也即权重向量）与式（4）联立，可建立第n 种方案的综合评估矩阵[6]：

令Qi（i=1，2，…，n）为第i 种比选方案的评价结果，wj（j=1，2，…，m）为第j 个指标因子的权重，则有：

3 作业方案比选

3.1 项目概况

越南某风电项目，位于沿海平原潮间带，是含设计、采运、施工于一体的EPC 工程,施工结束后因一台风机三支叶片受损被提出需修复或更换，否则将影响到未来运行安全。

3.2 各方案综合指标

基于项目研讨结果，可归纳出各方案不同指标的成本值、修复占用天数；技术、安全指标依托定性判断得出模糊量化值[7]，见表2。

表2 比选方案各因子指标信息

4 方案择优模型分析

4.1 方案评估模型

基于各方案特点所确定的关键评价指标多为定性的，具有一定的模糊性[8]。从工期损耗、采运费、服务费、技术可行性及安全性等各方面评估，可分10 类评价因子。评价模型如图1所示。

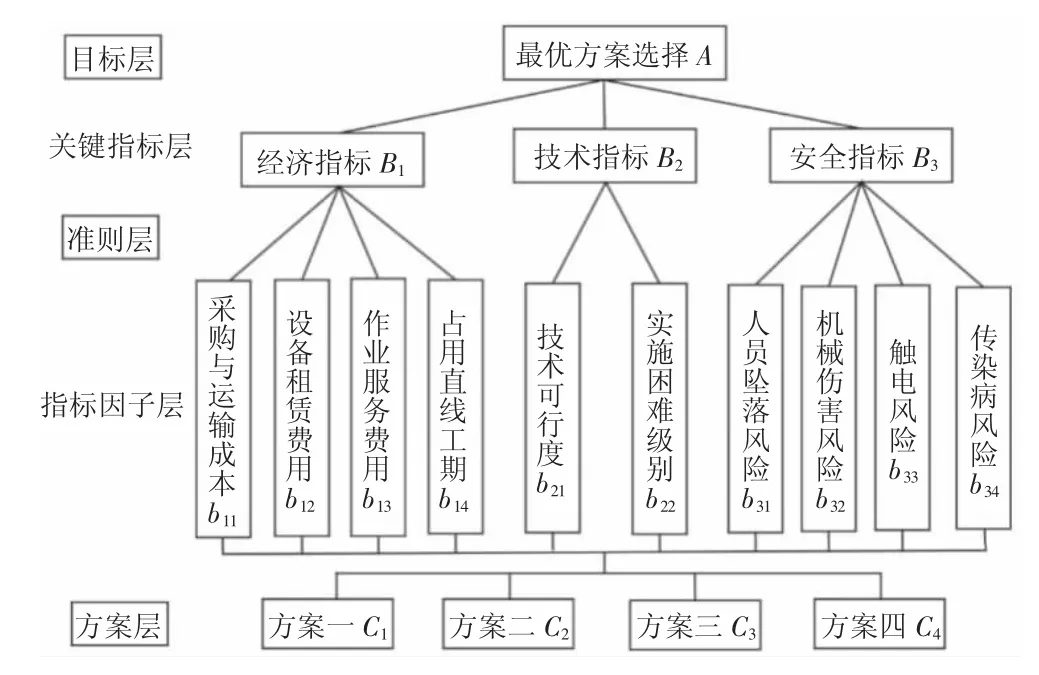
图1 比选方案层次评价体系

4.2 构建判断矩阵，确定指标权重W

基于图1 的层次模型结构，借助指数标度法，对上述4 个方案进行比选，详见表3～表6。

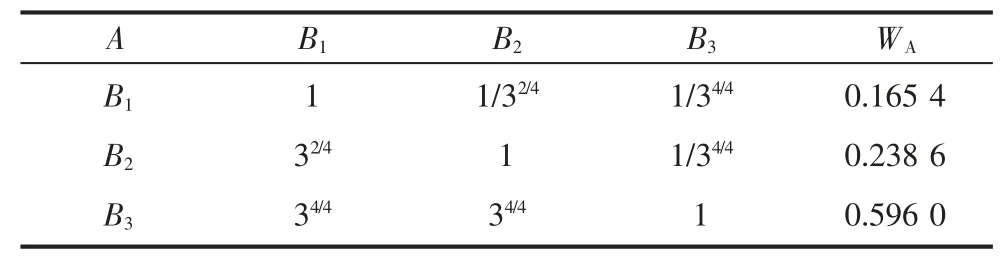
表3 判断矩阵A-B 及W 值

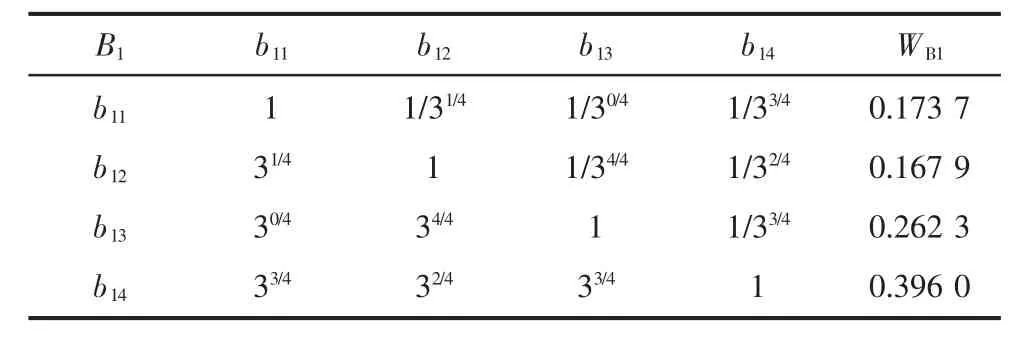
表4 判断矩阵B1-b1 及W 值

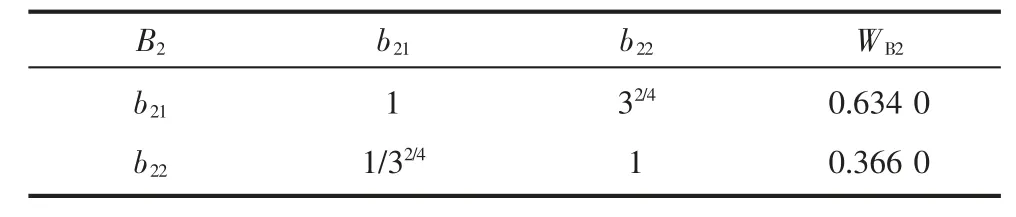
表5 判断矩阵B2-b2 及W 值

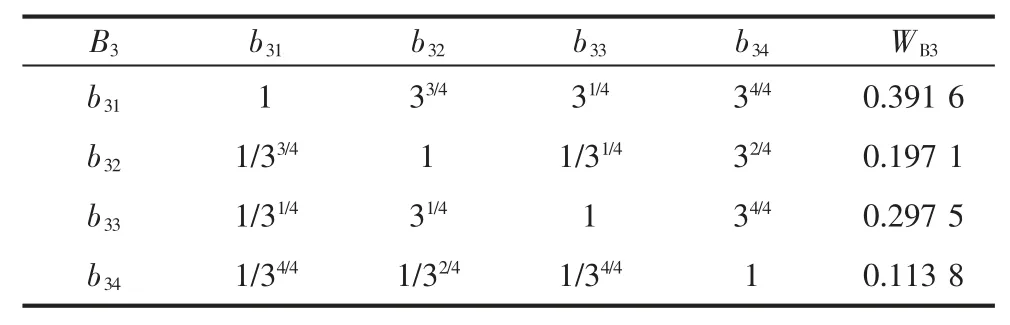
表6 判断矩阵B3-b3 及W 值

对判断矩阵进行一致性检验，见表7，其中，n 为矩阵阶数，λmax为该矩阵最大特征根，CI 为一致性指标，CR 为一致性比率。

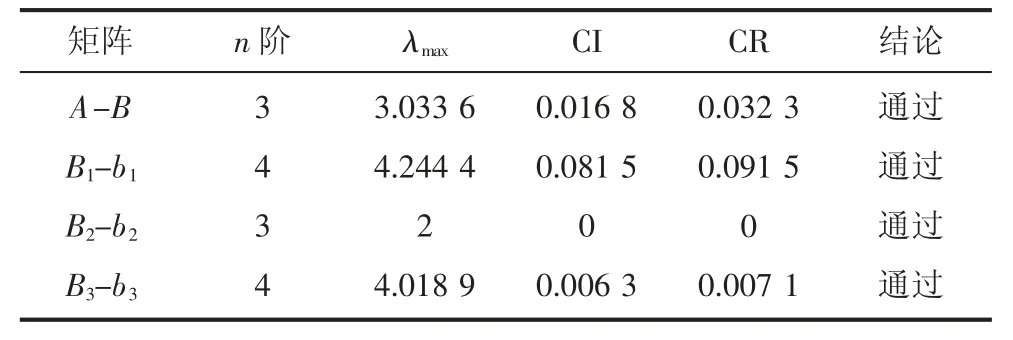
表7 判断矩阵一致性检验

求综合评价系数矩阵，如表8 所示。

表8 综合评价系数

由表8 可知，Γc3>Γc4>Γc2>Γc1，即最佳是方案三。

5 结论

1）识别出的关键性指标及其因子是构建理想层次模型、实现有效理论计算的前提，进而为后续实际实施进程中的工程管控做好充分准备工作。

2）利用GRA 理论规避了AHP 理论的主观因素影响，简化标度法，结合关联系数的修正得到更符合期望的理论值，而叶片更换最终达到了预期结果，也佐证了该理论模型具备一定实践性，为今后风机受损设备的更换或大量退役组件拆换的最优方案选择可提供一定指导价值。