高剪跨比榫卯连接装配整体式剪力墙受力性能数值分析

赵士瑞，孙志娟，刘继良

(1.北京建筑大学北京未来城市设计高精尖创新中心，北京 100044；2.大连理工大学土木工程学院，辽宁 大连 116024)

1 引言

装配式混凝土剪力墙结构是目前装配式混凝土建筑中采用的主要形式之一[1]。榫卯连接装配整体式剪力墙结构（简称“榫卯剪力墙”）是一种以“榫卯板”作为基本装配单元的全预制装配式混凝土剪力墙结构[2-4]，榫卯板侧面不出筋的特殊构造能够提高预制构件的标准化、模数化程度，提高生产效率，降低生产成本，使结构在生产应用的过程中具备突出优势[5]。

如图1 所示，榫卯板侧边间隔设置横向凸起作为榫头，榫头内开设竖向贯通孔洞作为榫孔，二者相交形成榫卯构造。相互连接时需将榫卯板的榫卯构造相对布置，在榫头间横向凹槽内设置连接钢筋，在榫孔内插入竖向钢筋，绑扎形成钢筋骨架，随后浇筑混凝土实现连接。

装配式混凝土剪力墙结构的剪跨比是决定剪力墙破坏形式的重要参数[6]。孙志娟[7]等通过对不同剪跨比的榫卯剪力墙进行拟静力试验，研究了剪跨比对墙体受力性能的影响，结果表明，低剪跨比（剪跨比1.0）的榫卯剪力墙没有发生剪切破坏，随着剪跨比的提高，墙体的承载力降低，但抗变形能力提升。曹春利[8]等利用ABAQUS 精细化数值分析模型研究了边缘构件纵向钢筋配筋率对低剪跨比榫卯剪力墙受力性能的影响，结果表明，随着边缘构件纵向钢筋配筋率的提高，低剪跨比墙体承载力显著提高，但增幅明显放缓。初明进[9]、李祥宾[10]等通过拟静力试验研究了轴压比和水平钢筋配筋率对中高剪跨比（剪跨比1.5）榫卯剪力墙的受弯性能的影响，结果表明提高水平钢筋配筋率和增大轴压比，均会使中高剪跨比榫卯剪力墙承载力及刚度有所增大，根部混凝土压溃区域面积减小。

综上，剪跨比对榫卯剪力墙的受力性能和破坏形式均有所影响。但目前研究多以低剪跨比和中高剪跨比榫卯剪力墙为对象，针对高剪跨比（剪跨比2.0）榫卯剪力墙受力性能的研究较少，为进一步探究高剪跨比榫卯剪力墙的受力性能和破坏形式，本文采用ABAQUS 有限元分析软件建立了高剪跨比榫卯剪力墙的精细化有限元分析模型，通过分析骨架曲线、破坏形态等，明晰了高剪跨比榫卯剪力墙的破坏过程，期望对榫卯剪力墙在工程中的生产设计提供参考依据。

2 试验概况

本文对文献[11]中榫卯剪力墙试件SCW-R2 进行精细化有限元建模，通过与试验现象的对比来进行模型的合理性验证。

试件SCW-R2 为轴压比0.15，剪跨比2.0 的榫卯剪力墙试件，其截面尺寸及配筋情况如图2 所示。墙体截面尺寸为1 500 mm×200 mm，由榫卯板和两侧现浇边缘构件组成。试件顶部设置加载梁，截面尺寸为300 mm×300 mm，试件底部设置地梁，截面尺寸为600 mm×650 mm。

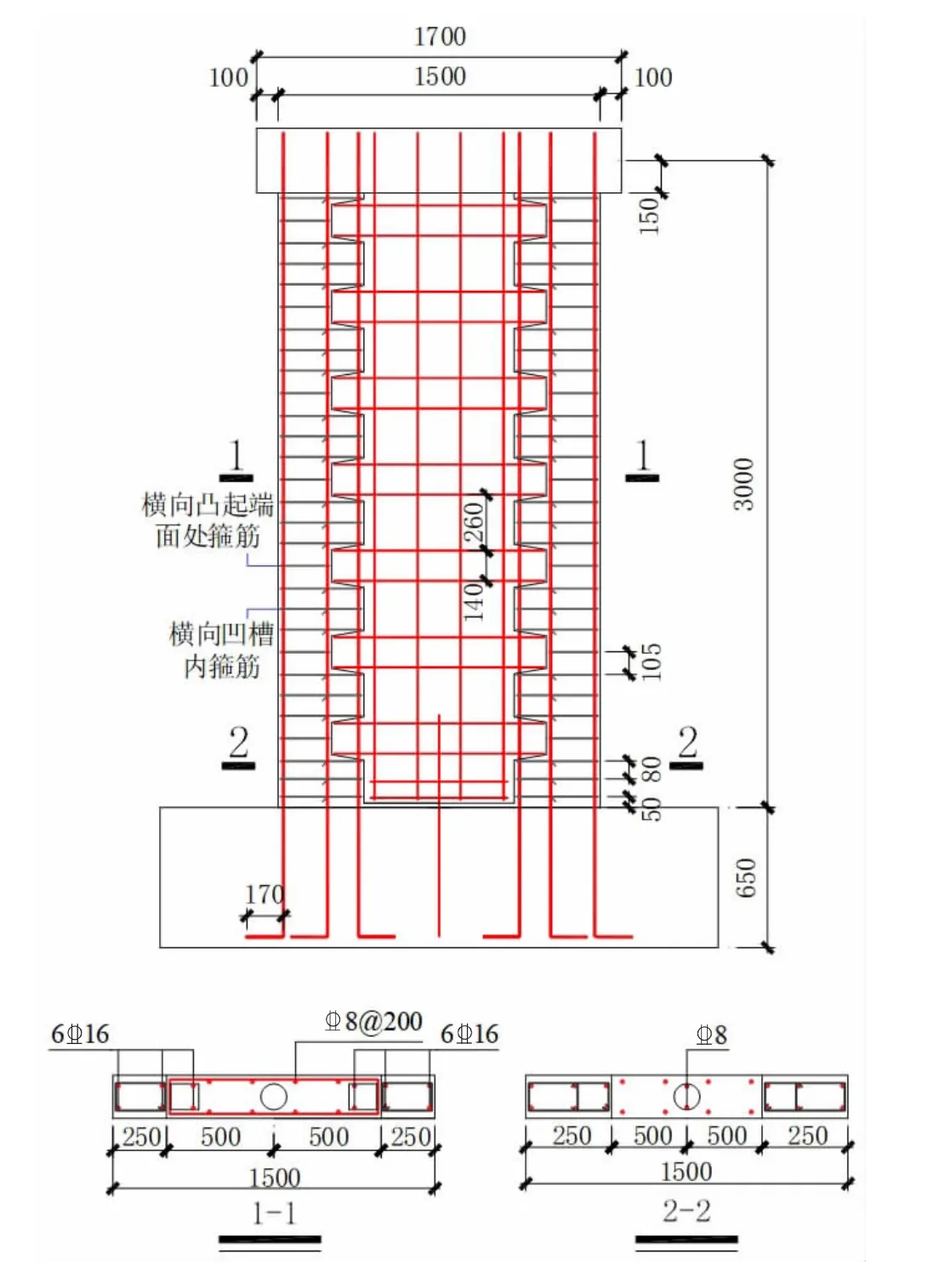
图2 试件SCW-R2 截面尺寸及配筋情况

预制混凝土与后浇混凝土的强度等级均为C30，其中预制混凝土强度实测值为46.33 MPa，后浇混凝土强度实测值为33.30 MPa，钢筋均采用HRB400 级，具体力学性能指标见表1。

表1 钢筋力学性能指标

3 模型建立

3.1 模型建立及网格划分

对试件SCW-R2 中的预制混凝土、后浇混凝土以及钢筋骨架进行分离式模型建立，混凝土采用八节点线性减缩积分三维实体单元（C3D8R 单元），钢筋采用取二节点三维桁架单元（T3D2 单元）。为突出分析重点，对墙体及钢筋骨架模型以50 mm 进行网格划分，对加载梁和地梁模型以100 mm 进行网格划分，如图3 所示。

图3 试件SCW-R2 模型建立

3.2 材料本构

试件SCW-R2 的混凝土本构模型采用塑性损伤模型，其中混凝土泊松比取0.2，预制混凝土和后浇混凝土的初始弹性模量分别为33 905 N/mm2和30 845 N/mm2，混凝土受压、受拉应力-应变关系曲线根据规范[12]进行定义，受压、受拉损伤因子参考文献[13]进行计算，塑性变形参数设置见表2，其中fb0/fc0为双轴屈服强度和单轴初始屈服强度的比值，K 为拉压子午面第二应力不变量。

表2 塑性变形参数设置

钢筋应力-应变关系采用双斜线模型，泊松比取0.3，屈服准则采用Von Mises 准则，钢筋弹性模量在弹性段取Es=2×105N/mm2，在钢筋屈服后的强化段取E's=0.01 Es。

3.3 新旧混凝土结合面相互作用

ABAQUS 中的库伦-摩擦模型、内聚力模型以及内聚力-摩擦混合模型均可用于新旧混凝土结合面的模拟[14-15]，但计算结果有一定差异[16]。

本文结合试件SCW-R2 的试验结果以及各接触模型的特点，选择库仑-摩擦模型来对模型中新旧混凝土结合面进行模拟，其剪应力τ-相对滑移s 曲线如图4 所示。设置时，切向行为中摩擦公式采用“罚”，摩擦系数μ 设为0.6[17]，法向行为采用“硬接触”，并在确定主从面时，将刚度较大的表面作为主面。

图4 库伦-摩擦模型

3.4 约束及边界条件

钢筋与混凝土之间设置Embedded 约束，不考虑二者之间的滑移。墙体上表面与加载梁之间以及墙体下表面与地梁之间均设置Tie 约束，地梁底部及侧面设置完全固定约束。

设置两个分析步来实现对试件的单调加载，Step-1 中设置集中力来模拟实验中恒定轴向荷载的施加，Step-2 中一方面存在Step-1 传递的集中力，另一方面设置边界条件来模拟实验中水平控制位移的施加。

4 有限元模拟结果

4.1 骨架曲线

试件SCW-R2 的试验骨架曲线与有限元模拟骨架曲线的对比如图5 所示，各特征点数值见表3，通过对比看出：试件SCW-R2 实际试验与有限元模拟的骨架曲线基本吻合，屈服荷载和峰值荷载的误差分别为9.69%和14.51%，屈服位移和峰值位移的误差分别为2.40%和8.74%，误差基本控制在10%左右。

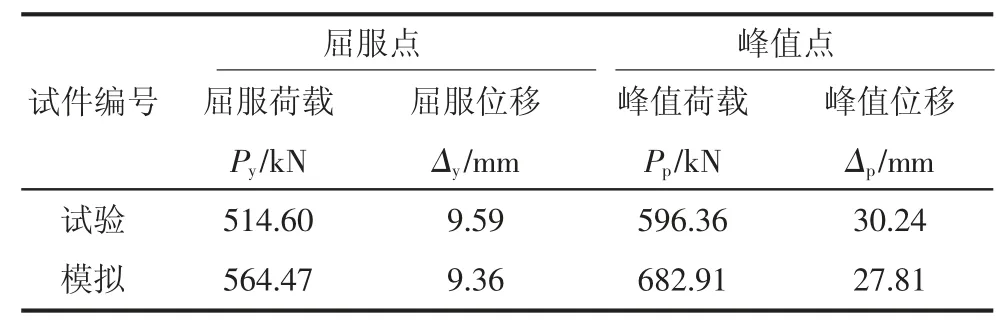
表3 各特征点数值

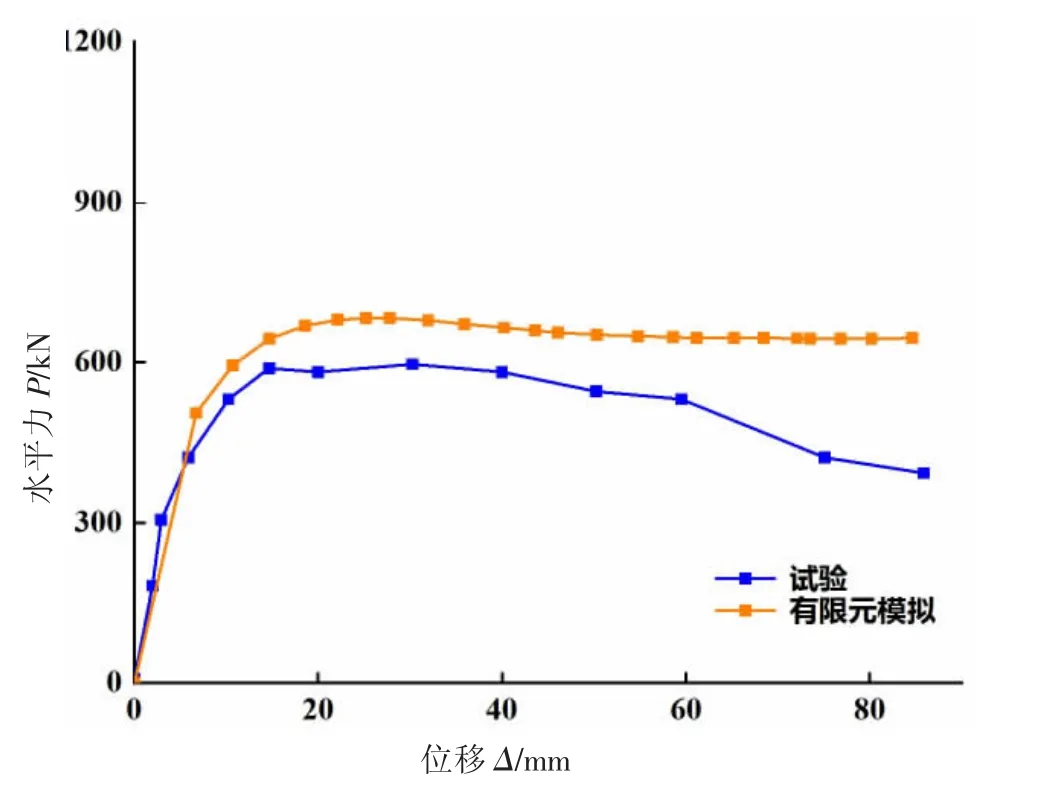
图5 试验与有限元模拟加载点水平力-位移骨架曲线对比图

4.2 破坏形态

最大主塑性应变云图能够直观的呈现出试件在加载过程中混凝土的开裂情况，可以在有限元模拟中用来表征试件的破坏形态。试件SCW-R2 在峰值状态、破坏状态（荷载下降至峰值荷载的85%或试验结束）时试验与模拟中破坏形态的对比如图6 和图7 所示，通过对比可以看出：

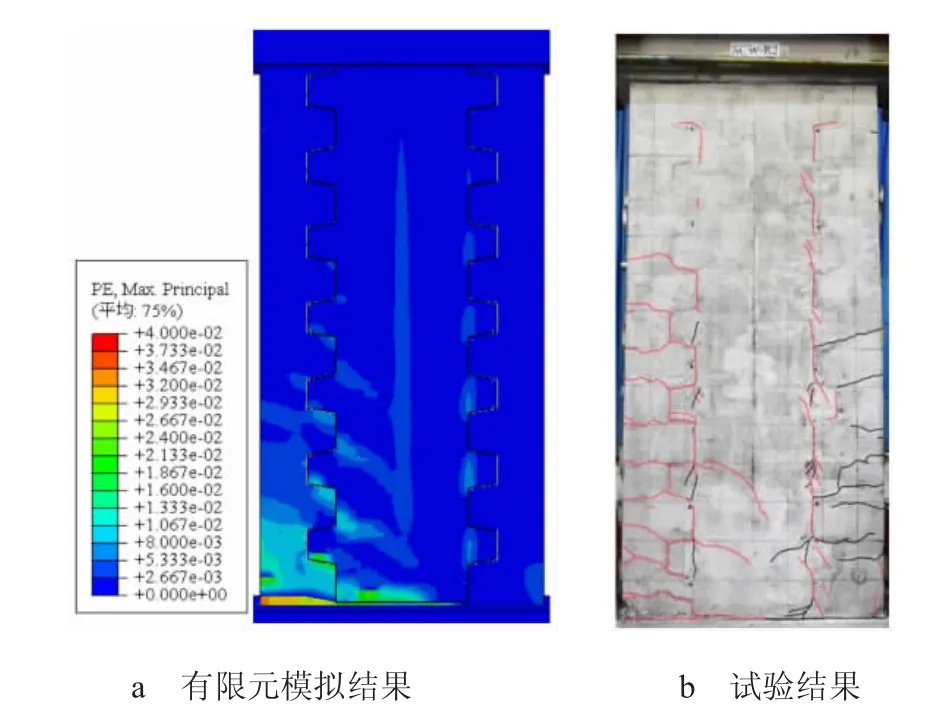
图6 峰值状态下的破坏形态对比

1）峰值状态时，墙体中部竖向贯通圆孔处交叉斜裂缝较少；东西两侧边缘构件出现水平裂缝，部分穿过榫卯接缝延伸至榫卯板表面；榫卯接缝处裂缝沿榫卯接缝的形状持续向上开展。

2）破坏状态时，墙体裂缝增多，墙体未出现对角斜裂缝，中部竖向贯通圆孔处出现多条交叉斜裂缝，东西两侧边缘构件水平裂缝持续沿墙高向上发展，墙体顶部出出现了与水平轴大概呈45°角的斜裂缝。

3）采用模拟结果中的最大主塑性应变云图表征的墙体破坏形态与试验中墙体的实际破坏形态基本一致。

5 结论

采用有限元软件ABAQUS 建立了高剪跨比榫卯剪力墙的精细化数值分析模型，对比了高剪跨比榫卯剪力墙试验与模拟的骨架曲线和破坏形态，主要结论如下。

1）结合试验结果以及各接触模型的特点，采用库仑-摩擦模型能够准确计算高剪跨比榫卯剪力墙中新旧混凝土结合面间的相互作用。

2）基于ABAQUS 软件建立的精细化数值分析模型合理，有限元模拟骨架曲线与试验结果吻合较好，模型破坏特征与试验现象基本一致，可用于之后的参数分析研究。