一种基于μ-S模型的最佳滑移率辨识估计器设计*

王 波,丁 芳,刘明岩,田苗法

(安徽机电职业技术学院汽车与轨道学院,安徽 芜湖 241002)

为了减少交通事故的发生,各大汽车厂商相继研究和开发了大量的汽车主动安全装置,从传统汽车的防抱死制动系统(Anti-Lock Braking System,ABS)到智能汽车的线控制动(Brake-by-Wire,BBW)系统,这些控制技术的实质都是调节汽车轮胎与路面的作用力,从而实现制动防抱死控制及车辆稳定性控制.该作用力除了受到轮胎结构的制约,还受到路面附着条件的影响.以汽车ABS为例,基于滑移率识别的控制方法才是最理想的控制策略[1-4],而该方法的前提是对各种不同路面条件下的最佳滑移率进行识别估计[5].不同路面条件下的轮胎路面μ-S特性曲线不同,对应最大路面摩擦系数的最佳滑移率也不同.如果仅凭经验或实验数据将最佳滑移率设定为某一平均值,那么即使防抱死控制器能迅速追踪滑移率并将其控制在目标滑移率附近,但因目标滑移率本身不是最优的,也会导致防抱死控制器无法实现最优控制[6].因此,从最优控制角度来说,实时辨识路面条件并获取最佳滑移率是基于滑移率防抱死控制策略实施的关键技术.近年来,学界对路面辨识技术作了大量研究[7-13],其中基于μ-S模型的识别方法[12-13]是目前国内外普遍接受的理论之一,其关键是在线辨识各种工况下的参数.为了使辨识估计参数少、耗时少,且较容易实现,笔者拟设计一款简单的最佳滑移率辨识估计器,期望辅助基于滑移率识别的防抱死控制器实现最优控制.

1 最佳滑移率与制动性能

图1 不同路面条件下纵向附着系数与滑移率的关系Fig. 1 Relationship Between Adhesion Coefficient and Slip Ratio of Different Pavements

路面的纵向附着系数(μx)对制动效果有直接影响,横向附着系数(μy)对防止侧滑和甩尾起决定性作用,μx和μy均与车轮滑移率有密切的关系.轮胎在不同路面条件下的纵向附着系数对应有最大值,这个值称为峰值附着系数(μh).图1示出了几种典型路面条件下纵向附着系数与滑移率之间的关系.

由图1可见,每种路面条件下都有一个峰值附着系数.这个峰值附着系数所对应的滑移率称为最佳滑移率(Sk).当滑移率处于最佳滑移率附近,纵向附着系数最大,车轮与路面之间的附着力最大,地面制动力最大,制动效果达到最佳状态.如果防抱死控制器始终将车轮滑移率控制在最佳滑移率附近,就能保证车轮与路面始终保持良好的附着力,也就能有效防止车轮抱死、侧滑、甩尾、失去转向等现象发生,从而保证制动时的方向稳定性.此外,防抱死控制器始终将制动力保持在最优范围内,这样能有效缩短制动距离,减轻轮胎磨损.

由于不同路面条件下的最佳滑移率不同,因此ABS最重要的目标就是设计一个可以实时追踪滑移率并控制在最佳滑移率的控制器,从而调节车轮的制动力,使轮胎与路面的摩擦力始终保持最大.在基于滑移率识别的汽车防抱死控制算法设计过程中,通常先要识别出各种路面条件下的最佳滑移率,将其作为滑移率目标值,再实现控制器对滑移率目标值的追踪控制,这样就能保证滑移率始终处于最佳滑移率附近,由此获得最佳制动力,实现最优控制.由以上分析可知,实时辨识路面特性并确定各种路面条件下的最佳滑移率,是传统液压制动系统及新型BBW系统研究的关键.基于最佳滑移率识别的汽车防抱死控制系统的基本原理如图2所示.

图2 基于最佳滑移率识别的汽车防抱死控制系统原理Fig. 2 Principle of ABS Based on Optimal Slip Ratio

2 最佳滑移率辨识估计器算法设计

目前,最佳滑移率的辨识估计方法大致分为以下3种:(1)基于参考滑移率的估计方法;(2)基于μ-S曲线形状的估计方法;(3)基于μ-S模型参数的估计方法.第1种方法将滑移率设定为固定值,通常不能实现最优控制;后2种方法能根据行车路况实时辨识估计最佳滑移率,其关键是模型的设计和模型参数的实时在线辨识估计[14].笔者将采用第3种方法,即基于μ-S模型结合递推最小二乘(Recursive Least Square,RLS)算法进行参数辨识估计.

2.1 常用μ-S曲线近似模型

不同路面条件下,汽车轮胎与路面的附着特性可借助一些μ-S经验模型来表示.轮胎模型通常可分为静态模型和动态模型[14]:静态模型是指附着系数(μ)只与滑移率相关,不呈现汽车行驶速度和车轮转速的模型,如Gim模型和魔术公式模型;动态模型是指附着系数不仅与滑移率有关,还能呈现汽车行驶速度和车轮转速的模型,如Burckhardt模型和Kiencke模型.

Burckhardt等[15]构建了一种简单实用的μ-S曲线动态模型,该模型被广泛应用于汽车制动控制算法中.其函数表达式为

μx(S)=c1(1-e-c2S)-c3S.

(1)

表1给出了7种典型路面条件下Burckhardtμ-S模型对应的3个参数(c1,c2,c3)的经验值.

表1 典型路面条件下的参数经验值

利用(1)式,最佳滑移率和峰值附着系数可通过求极值的方法得到:

(2)

理论上,只要能求解得到各种路面条件下的3个参数(c1,c2,c3),就能得到各种路面条件下的最佳滑移率及峰值附着系数.但在实际应用过程中,因为Burckhardtμ-S曲线函数的参数是非线性的,所以想要求解得到3个参数,就必须利用非线性的参数辨识估计方法,这给最佳滑移率的辨识估计带来一定的困难.

Kiencke等[16]构建了另一种简单实用的μ-S动态近似曲线模型,其函数表达式为

(3)

其中:k0为μ-S曲线斜率,一般取固定值30左右;P1,P2为待辨识估计参数.对(3)式求极值,同样可以求得Kienckeμ-S模型对应的最佳滑移率和峰值附着系数:

(4)

μ-S曲线中最重要的2个参数就是峰值附着系数和最佳滑移率.利用Burckhardt模型再结合(2)式虽然能得到μh和Sk,但是关系式较复杂,不同路面条件下的典型数字特征很难体现.观察Kienckeμ-S模型得到的(4)式,能清楚看出参数P1,P2与峰值附着系数和最佳滑移率之间的关系:最佳滑移率仅由参数P2决定,而峰值附着系数则受参数P1,P2共同影响.

由(3)式等效变换可得

k0S-μx=(μxSμxS2)(P1P2)T,

(5)

其中时变参数P1,P2可利用递推算法求解得到.这样,根据(4)式就可得实时修正的峰值附着系数和最佳滑移率.

2.2 改进遗忘因子RLS算法

在基于Kienckeμ-S模型的最佳滑移率识别算法中,关键的一个问题是时变参数P1,P2的辨识估计,这需要用到自适应递推算法.典型的自适应递推算法包括卡尔曼滤波(Kalman Filter,KF)算法、RLS算法和最小均方差自适应(Least Mean Square,LMS)算法[17].KF算法的优点是跟踪能力较强,缺点是需要事先确定相关噪声的统计参数,且计算量较大.RLS算法和LMS算法相比于KF算法,具有较强的噪声抑制能力,而RLS算法比LMS算法的收敛速度更快[17],因此本研究采用RLS算法.

汽车在制动过程中,由于路面条件差异会导致参数发生变化,因此传统RLS算法无法满足参数辨识要求.李言俊等[18]设计了遗忘因子算法.该算法的基本思想是将老数据乘以遗忘因子,由此降低老数据的影响,扩大新数据的影响.改进遗忘因子的快速时变参数辨识方法[19],主要是在传统辨识的基础上对遗忘因子作改进,能满足汽车制动系统这一类快速时变系统的参数估计要求.通常,改进后的辨识算法更优于传统RLS算法.

为了能根据路面特性得到快速修正的最佳滑移率,笔者设计了基于Kienckeμ-S模型的改进遗忘因子快速时变参数辨识方法.其原理如下:令

y(n)=k0S(n)-μx(n),

ΦT(n)=(μx(n)S(n)μx(n)S2(n)),

PT(n)=(P1(n)P2(n)),

则(5)式变为

y(n)=ΦT(n)P(n).

利用改进RLS算法,得到时变参数矩阵P(n)的递推公式

其中K(n+1)=Γ(n)Φ(n+1)Ψ(n+1).这里

Ψ(n+1)=(α+ΦT(n+1)Γ(n)Φ(n+1))-1.

参数α是遗忘因子,即衰减因子,主要用于描述衰减老数据的影响.

3 仿真实验

3.1 仿真模型建立

为了验证Kiecheμ-S模型结合改进遗忘因子RLS算法的最佳滑移率辨识估计器(简称“Kieche_RLS辨识估计器”)的识别效果,基于Matlab/Simulink工具建立Kieche_RLS最佳滑移率辨识估计器模型,如图3所示.

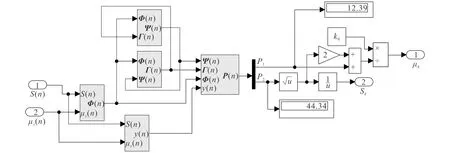
图3 Kieche_RLS最佳滑移率辨识估计器模型Fig. 3 Kieche_RLS Optimal Slip Ratio Identification Model

将Kieche_RLS最佳滑移率辨识估计器模型封装,搭建基于最佳滑移率识别的汽车ABS模糊滑模控制系统仿真模型(图4).图4中,FSMC(Fuzzy Sliding Mode Controller)为基于滑移率识别的汽车ABS模糊滑模控制器模型,Vehicle Model为车辆模型,Burckhardtμ-S为基于(1)和(2)式搭建的路面模型.

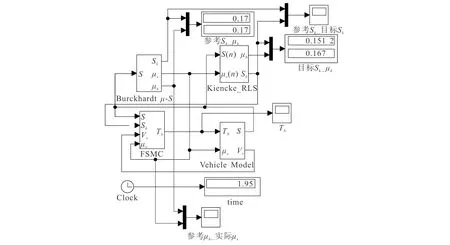
图4 基于最佳滑移率识别的汽车ABS模糊滑模控制系统仿真模型Fig. 4 Simulation Model Diagram of ABS Fuzzy Sliding Mode Control System Based on Optimal Slip Ratio Identification

仿真实验中,首先,由Burckhardtμ-S模型模拟各种典型的路面条件,并计算出最佳滑移率和峰值附着系数,以此作为参考值;然后,将Kieche_RLS辨识估计器识别的最佳滑移率和峰值附着系数(目标值)与参考值进行对比,比较误差大小;最后,将辨识估计器应用于汽车ABS的模糊滑模控制器中,验证最佳滑移率辨识估计器的有效性.

3.2 单一路面仿真结果

表2给出了几种典型路面条件下,最佳滑移率和峰值附着系数的Burckhardt模型参考值与Kiencke_RLS辨识估计器识别结果的对比情况.表2中:Sk参考和μh参考分别为基于Burckhardtμ-S模型计算得到的最佳滑移率和峰值附着系数,作为参考值;Sk目标和μh目标分别为Kieche_RLS辨识估计器识别的最佳滑移率和峰值附着系数.

表2 几种典型路面条件下Burckhardt模型参考值和Kiencke_RLS辨识结果

由表2可知,在单一路面条件下,Kieche_RLS辨识估计器识别的目标最佳滑移率及目标峰值附着系数与Burckhardt模型参考值基本一致,绝对误差较小.由于基于最佳滑移率识别的模糊滑模控制器能在线识别最佳滑移率,因此车轮纵向附着系数始终处于峰值附着系数附近,使得附着力最大化,实现了最优控制.这说明,最佳滑移率辨识估计器对单一路面是可行的.限于篇幅,仅给出干沥青、湿沥青及雪路面等单一路面的仿真结果(图5～10).

(1)高附着路面——干沥青路面仿真结果.

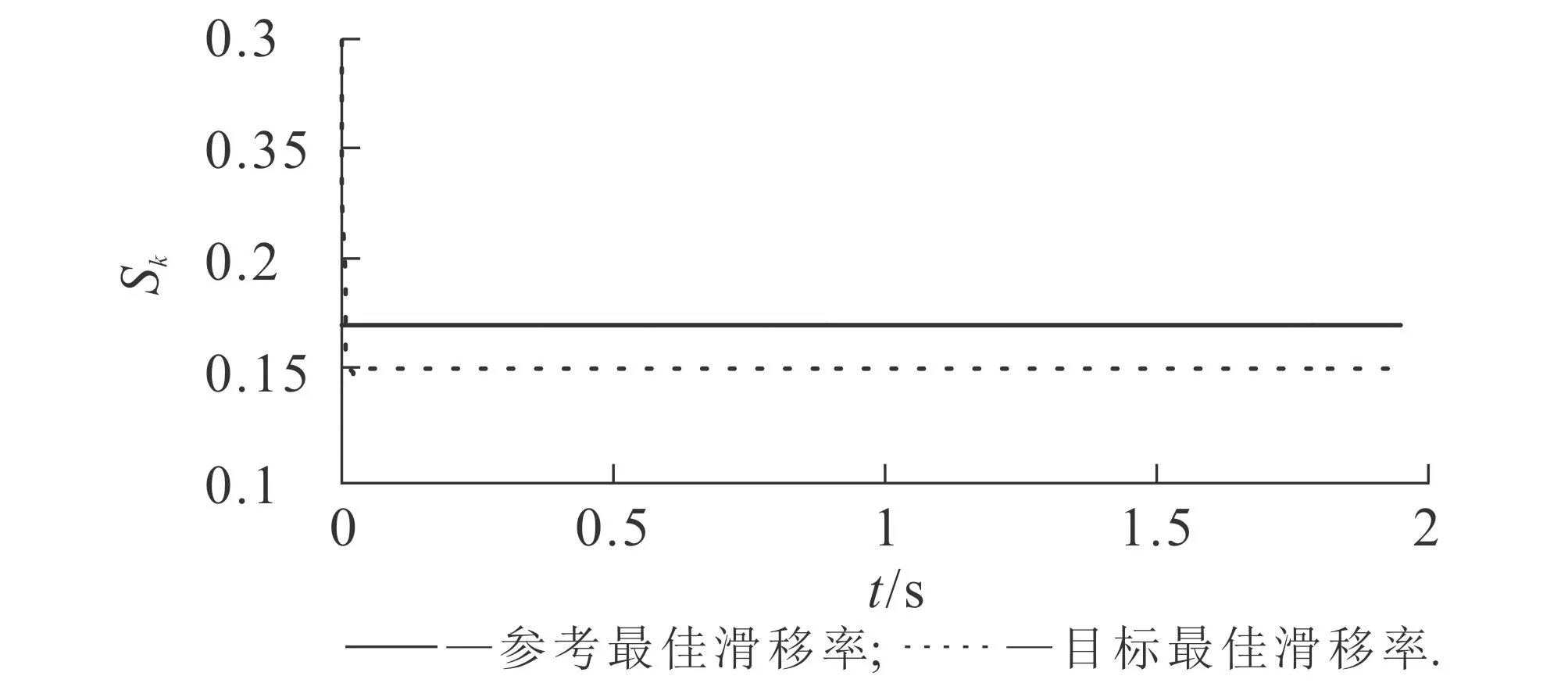
图5 干沥青路面条件下最佳滑移率的辨识结果Fig. 5 Identification Results of Optimum Slip Ratio for Dry Asphalt Pavement

图5示出了干沥青路面条件下最佳滑移率的辨识结果.由图5可知,Kieche_RLS辨识估计器识别的目标最佳滑移率为0.151 2,Burckhardt μ-S模型给出的参考最佳滑移率为0.170 0,二者比较接近.

图6示出了干沥青路面条件下,结合最佳滑移率辨识估计器的汽车ABS模糊滑模控制器的仿真结果.由图6可知:控制器能快速追踪辨识估计器识别的最佳滑移率并将滑移率保持在目标值;滑移率保持在目标最佳滑移率Sk目标=0.151 2时,实际纵向附着系数始终处于参考峰值附着系数附近(参考峰值附着系数为1.170 0,实际峰值附着系数为1.167 0).结合表2可知,滑移率保持在目标最佳滑移率Sk目标=0.151 2时,实际纵向附着系数始终处于目标峰值附着系数附近,制动时间少,制动距离短.

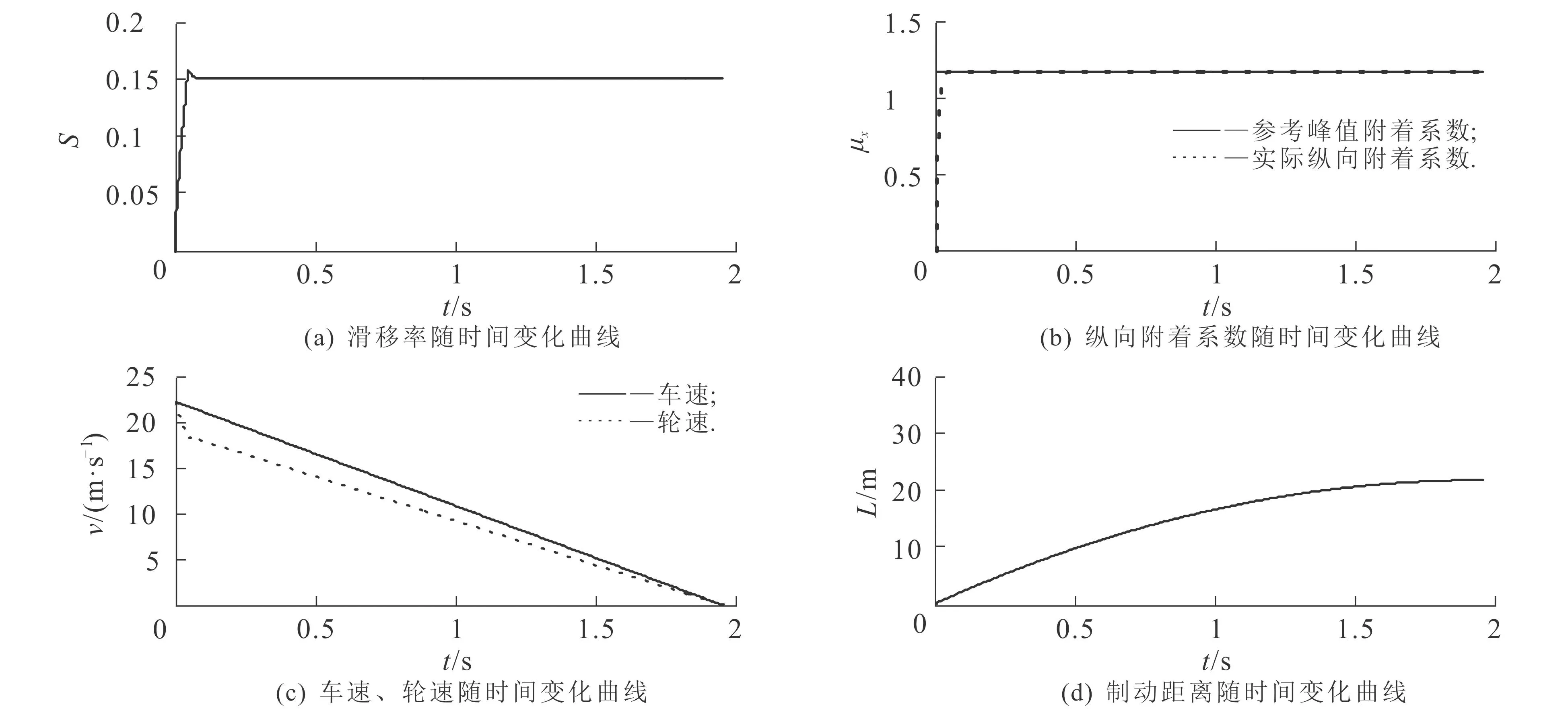
图6 干沥青路面条件下基于最佳滑移率识别的模糊滑模控制器的仿真结果Fig. 6 Simulation Results of FSMC Based on Slip Ratio for Dry Asphalt Pavement

(2)中附着路面——湿沥青路面仿真结果.

图7示出了湿沥青路面条件下最佳滑移率的辨识结果.由图7可知,Kieche_RLS辨识估计器识别的目标最佳滑移率为0.131 4,Burckhardtμ-S模型给出的参考最佳滑移率为0.130 8,二者非常接近.

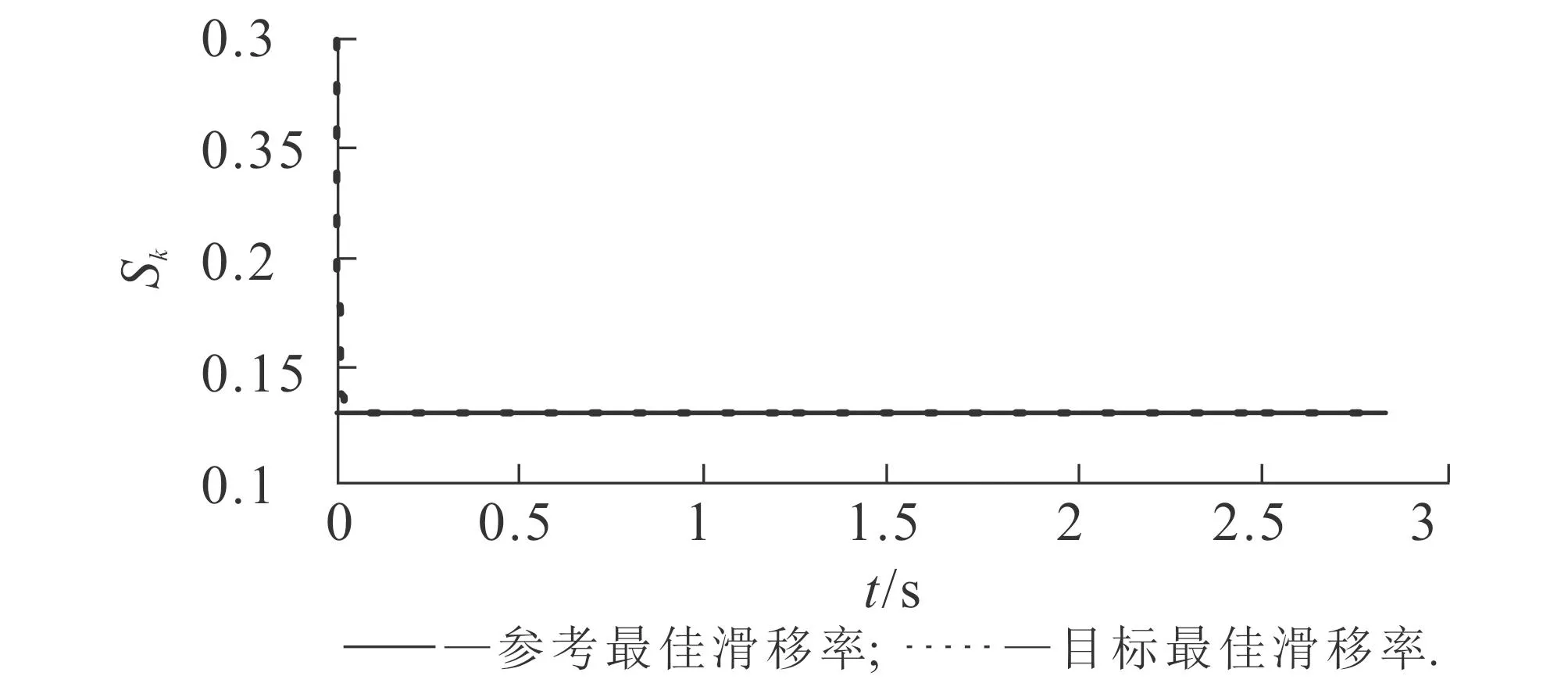
图7 湿沥青路面条件下最佳滑移率辨识结果Fig.7 Identification Results of Optimum Slip Ratio for Wet Asphalt Pavement

图8示出了湿沥青路面条件下,结合最佳滑移率辨识估计器的汽车ABS模糊滑模控制器的仿真结果.由图8可知:控制器能快速追踪辨识估计器识别的最佳滑移率;滑移率保持在目标最佳滑移率Sk目标=0.131 4时,实际纵向附着系数与参考峰值附着系数一致(参考峰值附着系数和实际峰值附着系数同为0.801 3).结合表2可知,滑移率保持在目标最佳滑移率Sk目标=0.131 4时,实际纵向附着系数与目标峰值附着系数一致,制动时间少,制动距离短.

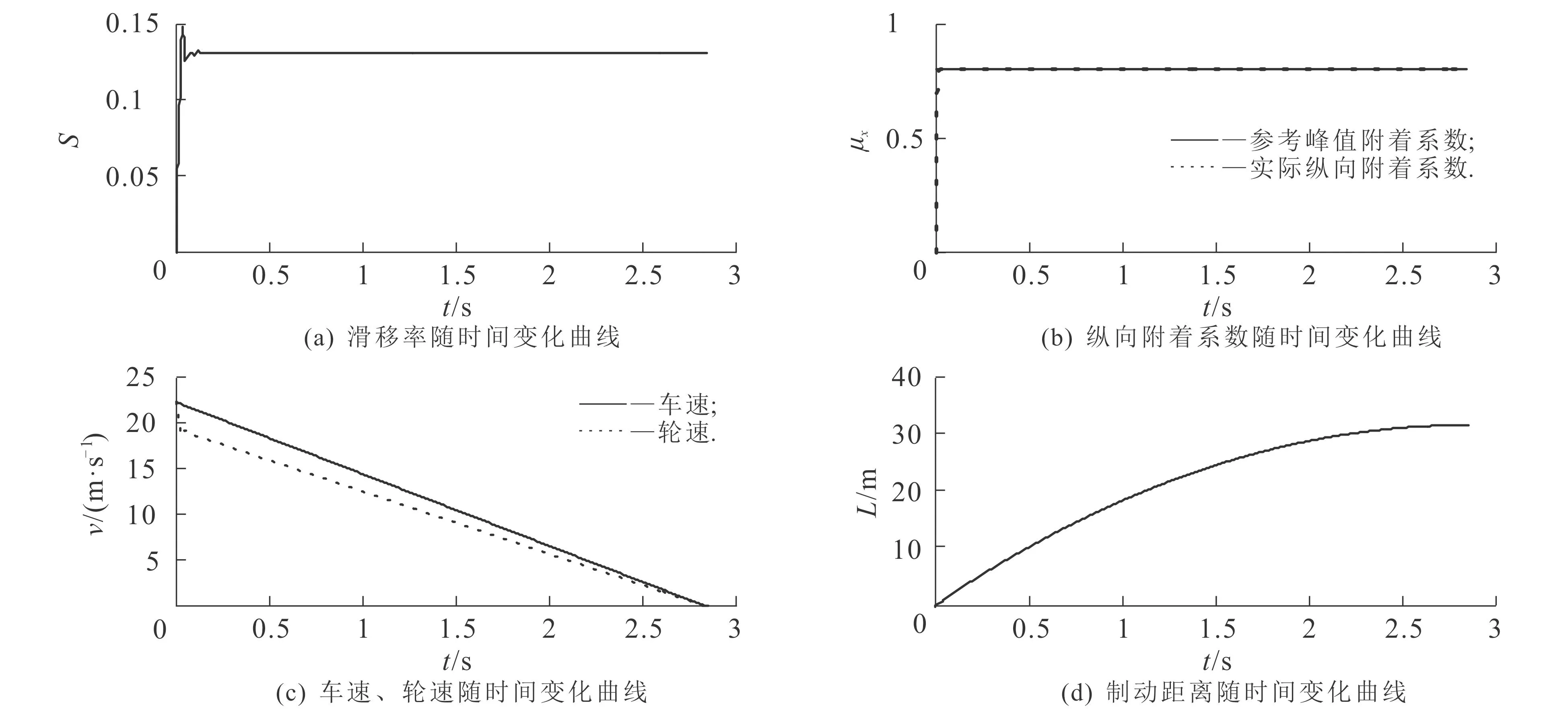
图8 湿沥青路面条件下基于最佳滑移率识别的模糊滑模控制器的仿真结果Fig. 8 Simulation Results of FSMC Based on Slip Ratio for Wet Asphalt Pavement

(3)低附着路面——雪路面仿真结果.

图9 雪路面条件下最佳滑移率辨识结果Fig. 9 Identification Results of Optimal Slip Ratio for Snow Pavement

雪路面属于典型的低附着路面,制动过程中极易发生抱死现象.图9示出了雪路面条件下最佳滑移率的辨识结果.由图9可知,Kieche_RLS辨识估计器识别的目标最佳滑移率为0.073 2,Burckhardtμ-S模型给出的参考最佳滑移率为0.060 0,二者比较接近.

图10示出了雪路面条件下,结合最佳滑移率辨识估计器的汽车ABS模糊滑模控制器的仿真结果.由图10可知:在低附着路面条件下,控制器依然能快速追踪辨识估计器识别的最佳滑移率;滑移率保持在目标最佳滑移率Sk目标=0.073 2时,实际纵向附着系数始终处于参考峰值附着系数附近(参考峰值附着系数为0.190 0,实际峰值附着系数为0.189 7).结合表2可知,滑移率保持在目标最佳滑移率Sk目标=0.073 2时,实际纵向附着系数始终处于目标峰值附着系数附近,车轮没有抱死现象.

图10 雪路面条件下基于最佳滑移率识别的模糊滑模控制器的仿真结果Fig. 10 Simulation Results of FSMC Based on Slip Ratio for Snow Pavement

3.3 跃变路面仿真结果

图11 跃变路面条件下最佳滑移率辨识结果Fig. 11 Identification Results of Optimal Slip Ratio for Variational Pavement

汽车在行驶过程中经常会经历跃变路面的制动行驶.为了了解辨识估计器在跃变路面条件下的识别情况,仿真过程中车辆在湿沥青路面上行驶1 s后进入干沥青路面.图11示出了跃变路面条件下最佳滑移率的辨识结果.由图11可知,在跃变路面条件下,Kieche_RLS辨识估计器识别的目标最佳滑移率与Burckhardtμ-S模型给出的参考最佳滑移率基本一致,误差较小,延迟也较小.

图12示出了跃变路面条件下,基于最佳滑移率识别的模糊滑模控制器的仿真结果.由图12可知:在跃变路面条件下,控制器依然能较快速追踪到最佳滑移率的突变;制动过程中,滑移率保持在目标滑移率(Sk目标由0.131 4向0.151 2变化)时,实际纵向附着系数始终处于参考峰值附着系数附近.结合表2可知,滑移率保持在目标最佳滑移率(Sk目标由0.131 4向0.151 2变化)时,实际纵向附着系数始终处于目标峰值附着系数附近,车轮没有抱死趋势,制动时间较少,制动距离较短,制动效能有效提升.

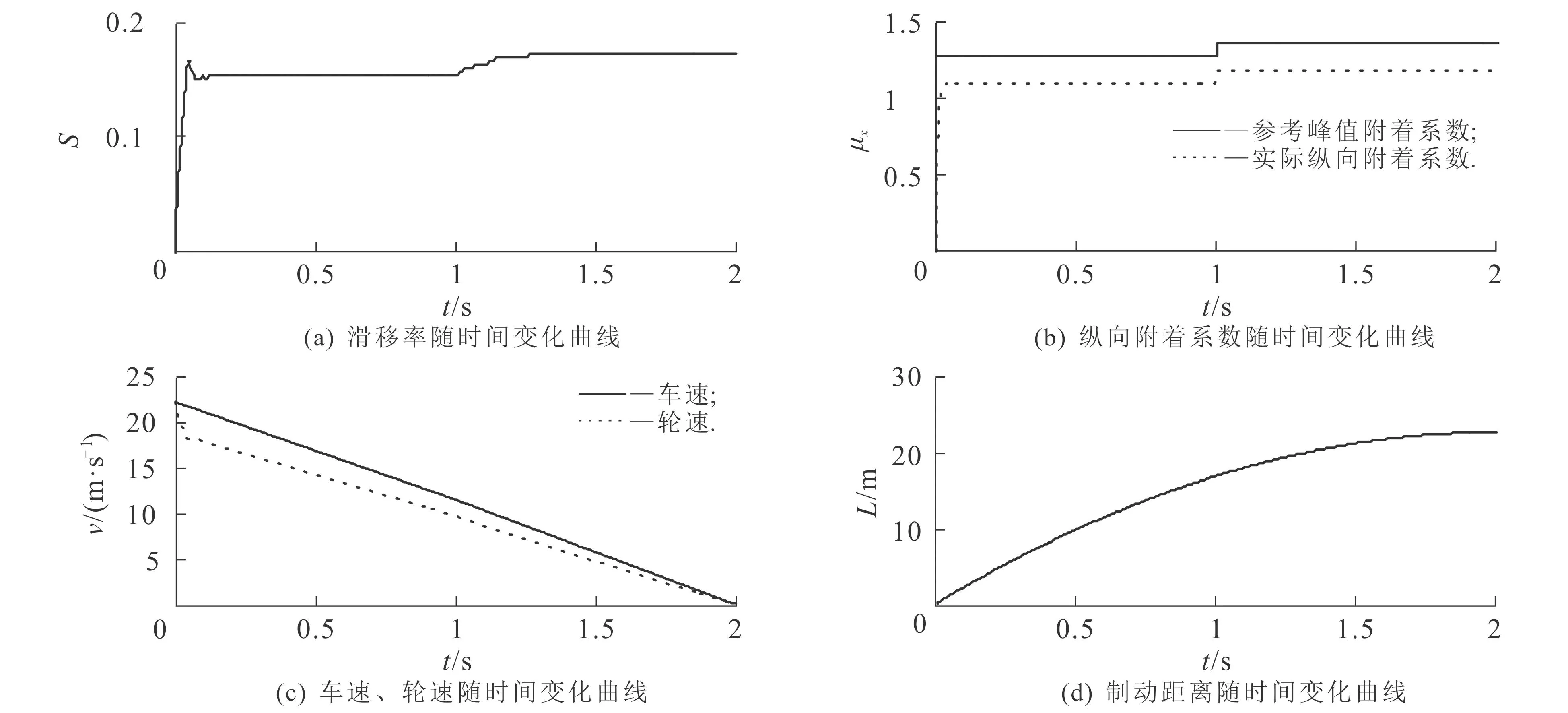
图12 跃变路面条件下基于最佳滑移率识别的模糊滑模控制器的仿真结果Fig. 12 Simulation Results of FSMC Based on Slip Ratio for Variational Pavement

4 结语

基于Kienckeμ-S模型并结合改进遗忘因子RLS算法设计了最佳滑移率辨识估计器.该辨识估计器能够实现单一路面和跃变路面条件下最佳滑移率的识别,兼具误差小、延迟小的特点.将辨识估计器应用于汽车ABS的模糊滑模控制器中,对滑移率、纵向附着系数、车速/轮速、制动距离等进行仿真实验.实验结果表明,结合最佳滑移率辨识估计器的防抱死控制器能够快速识别并追踪目标滑移率,使滑移率始终处于最佳滑移率附近,纵向附着系数始终处于峰值附着系数附近,车轮没有抱死现象,制动时间少,制动距离短,制动效能有效提升.辨识估计器辨识参数少,易于实现,适用于基于滑移率识别的汽车防抱死制动控制系统,包括液压制动系统、线控制动系统等,有一定的应用前景.