融合邻域分布LLE算法轴承故障信号检测

张彦生,张利来,刘远红

(东北石油大学 a.电气信息工程学院; b.东北石油大学国家大学科技园,黑龙江 大庆 163318)

0 引 言

电机是现代重要的生产设备动力装置,维持电机正常运行对社会的经济发展具有重要意义。而电机轴承是电机较易损坏的零件之一[1],因此高效地检测电机轴承运行状态是非常必要的[2-3]。随着信息技术的快速发展,电机轴承故障诊断过程中涉及到大量高维数据,分析与处理这些数据对及时发现并反馈问题,避免出现规模性的经济损失,提高生产效率具有重要意义。然而,高维数据中包含大量的冗余信息,同时维数的增加会引起“维数灾难”[4],这都将对数据的处理和分析造成不利的影响。

由于电机轴承数据在高维空间为流形结构,线性降维算法不能对其进行有效处理,因此利用非线性降维算法成为处理电机轴承数据的关键。LLE(Local Linear Embedding)是非线性降维的关键技术之一,因其良好的性能和简单性而引起了人们的广泛关注。但LLE仍存在没有充分挖掘局部结构的缺陷,针对该问题,学者们提出了基于更换欧氏距离和多种算法组合技术。由于在高维流形上欧氏距离的局限性,更换欧氏距离的方法,能实现对高维流形结构的精准度量。Pan等[5]利用伽玛函数和新的加权距离公式改善LLE,在数据的分布与高斯分布差距较大时表现良好。Varini等[6]将等距特征映射算法ISOMAP(Isometric Feature Mapping)中的测地线距离引入LLE中用于构建K最近邻法KNN(K-Nearest Neighbor)图,得到ISOLLE(Isometric Locally Linear Embedding)算法。将数据映射到不同的空间同样能达到挖掘高维数据结构的作用。Zhang等[7]则利用LLE和线性判别分析LDA(Linear Discriminant Analysis)相结合得到ULLELDA算法(Unified Locally Linear Embedding and Linear Discriminant Algorithm)。Jiang等[8]将LLE与主成分分析(PCA:Principal Component Analysis)相结合得到 LLE-PCA算法。近年来,利用邻域拓扑关系增强对邻域结构的挖掘。例如,Kong等[9]提出的迭代LLE,该算法是一种利用包含对角矩阵的强化线性嵌入的LLE优化方法。Luo[10]等提出用混合图学习方法能有效地揭示高维数据之间的内在关系,Luo[11]还提出了一种多结构统一判别嵌入方法,该方法考虑高光谱图像集中每个样本的邻域、切向和统计特性,以实现不同特征的互补。

但上述方法仅挖掘原始空间的拓扑关系,并未考虑邻域和邻域之间的拓扑关系,因此在很多数据中不利于维持原始数据在低维空间的结构关系。为充分挖掘电机轴承信号的高维空间结构,笔者提出了一种新的融合邻域分布属性的局部线性嵌入算法,即利用高斯分布将每个最近邻样本与中心样本之间的相似度转换为最近邻样本的条件概率。通过计算每个邻域样本与其邻域中心点临近点分布的KL(Kullback-Leibler)散度,度量中心点与近邻点各自邻域分布的相似度。最后,权重修正函数调整权重系数,实现了对高维数据邻域间结构的挖掘。

1 局部线性嵌入算法

LLE算法是经典局部流形学习算法,其核心思想是找到每个高维流形上样本点的近邻域样本,并用其线性重构该样本点,以此挖掘高维数据局部的拓扑结构信息。高维样本数据集为X=[x1,x2,…,xN]∈RD×N,其中xi(i=1,2,…,N)为第i个样本,D为高维样本的特征维数,N为样本总数。设低维映射结果为Y=[y1,y2,…,yN]∈Rd×N,d为低维空间的维数。LLE算法具体计算步骤[12]如下。

步骤1) 设定邻域大小超参数为K且假设较小局部中的数据是线性的,针对每个样本点,选择与其相似度最高的前K个样本点作为近邻点。

步骤2) 利用样本xi与周围K个近邻点,通过最小化均方差计算每个样本点的重构权重w,计算函数如下:

(1)

其中n(i)为第i个样本邻域。通过高维重构权重计算样本点的低维输出,低维空间的线性重构公式如下:

(2)

2 融合邻域分布属性的局部线性嵌入算法

针对LLE算法未能充分保持高维数据邻域之间结构的问题,笔者提出了一种融合邻域分布的属性的局部线性嵌入算法DLLE(Local Linear Embedding algorithm incorporating the properties of the neighborhood Distribution),通过加强分布属性相似邻域的权重,提高降维效果。首先,对每个样本点,选择相似度最高的前K个样本点作为最近邻点。计算每个样本xj在xi邻域中对应的高斯分布概率[13]:

(3)

则对以xj为中心的邻域样本xjj的高斯分布概率为

(4)

其次,将样本xi的邻域分布设为Li,其邻域样本xj的邻域分布设为Lj。由散度计算其之间的分布差异。相应的散度公式为

(5)

归一化散度函数为

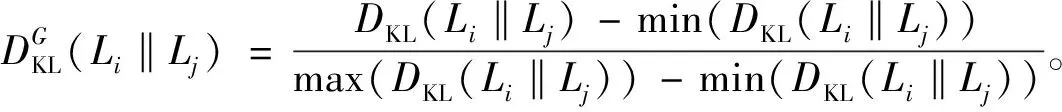
(6)

鉴于LLE算法没有考虑到样本邻域分布之间的差异,通过在原始的降维过程中添加对权重w的修正函数,使邻域Li与Lj分布的相似性关系信息传送到低维空间。修正函数如下:

(7)

其中α为修正系数(0<α<1),通过调整其大小可以控制高维数据邻域分布相似性关系对低维数据的影响。图1为KL散度度量邻域分布的示意图。

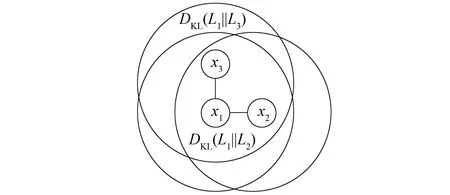
图1 KL散度度量邻域分布

为满足低维数据的生成条件,每个样本的权值之和为1,因此有:

(8)

3 实验仿真及结果分析

为评估DLLE算法应用在电机轴承信号检测上的效果,利用DLLE算法对两个轴承故障数据集的实验结果数据进行评估。由可视化、定量聚类和识别精度评估3个实验验证该方法在可视化、数据分类与识别精度,从而验证DLLE算法具有较强的电机轴承信号数据高维空间结构的挖掘能力。

3.1 数据集

为充分证明算法的广泛有效性,使用分别来自凯斯西储大学CWRU(Case Western Reserve University)和江苏千鹏公司生产的QPZZ-Ⅱ型轴承故障诊断设备实验平台采集的两组滚动轴承数据集。

CWRU数据集采样平台如图2所示,包括一个2马力1.5 kW的电机,一个转矩传感器,一个功率测试计与电子控制设备(图2中未显示)。待检测的轴承支撑着电动机的转轴,驱动端转轴为SKF6250,风扇端轴承为SKF6203。安装在基座上的加速度传感器在负载为0,频率为12 kHz,转子转速为1 720 r/min的情况下进行采集,包含正常、滚珠故障、轴承内圈故障和外圈故障4类数据,且每种数据采集100个样本,每个样本包含1 024个特征。

图2 CWRU数据集采样平台

千鹏数据集采样平台如图3所示,平台由电机、轴承和齿轮箱组成,传感器在无负载,电机采样频率为10 kHz,转速为1 400 r/min的情况下,共采集正常、滚珠故障、轴承内圈故障和外圈故障数据,每种数据有100个样本,每个样本有1 024个特征。

3.2 效果可视化评估

利用LLE、局部切空间排列LTSA(Local Tangent Space Alignment)、拉普拉斯特征映射LE(Laplacian Eigenmaps)和DLLE 4种降维算法在两种数据集上的三维效果进行对比,其中正方形代表正常数据,菱形代表内圈故障数据,五角星代表滚珠故障数据,三角形代表外圈故障数据。4种电机数据由于特征不同,在高维空间中处于不同的区域。在降维过程中,由于没有保留高维数据中邻域之间的结构,导致在低维空间不能有效反应不同种类数据之间的空间关系,即不同种类数据发生相互堆叠。因此,通过不同算法能否有效分离同一数据集,可以有效判断算法的保留高维数据中邻域之间的结构能力。

不同降维算法处理CWRU数据结果如图4所示,在多种降维算法处理CWRU数据的三维效果中,图4a为LLE算法处理得到的低维结果,外圈故障数据集中,其余3种数据分散,数据堆叠情况严重,没有明显的汇集点。LTSA处理效果如图4b所示,低维结果均比较聚集,呈现柱状分布,4种数据间具有明显的汇集点。图4c是LE算法的处理的可视化效果图,能明确反映外圈故障数据,正常数据被分为两个部分,另外两种数据堆叠严重,不能有效区分。DLLE算法效果如图4d所示,同类数据均聚集为一点,且不同种类之间分散,基本没有发生数据堆叠。

图4 不同降维算法处理CWRU数据结果

不同降维算法处理千鹏数据结果如图5所示。在其三维效果中,LLE算法处理得到的低维结果如图5a所示,4种故障汇集成柱状,有明显的交叉部分。LTSA处理效果中,不同种类数据仍然集中,如图5b所示。图5c表明LE算法难以区分正常和外圈故障数据。DLLE算法效果如图5d所示,正常和外圈故障数据呈现柱状分布,滚珠故障和内圈故障数据聚集呈点状分布,低维数据仍然无明显堆叠现象。综上,LLE、LTSA和LE通过处理CWRU数据与千鹏数据得到的4种数据发生堆叠现象,DLLE的低维结果正确反映高维数据空间分布,表明其提高了LLE保留高维数据中邻域之间的结构的能力。

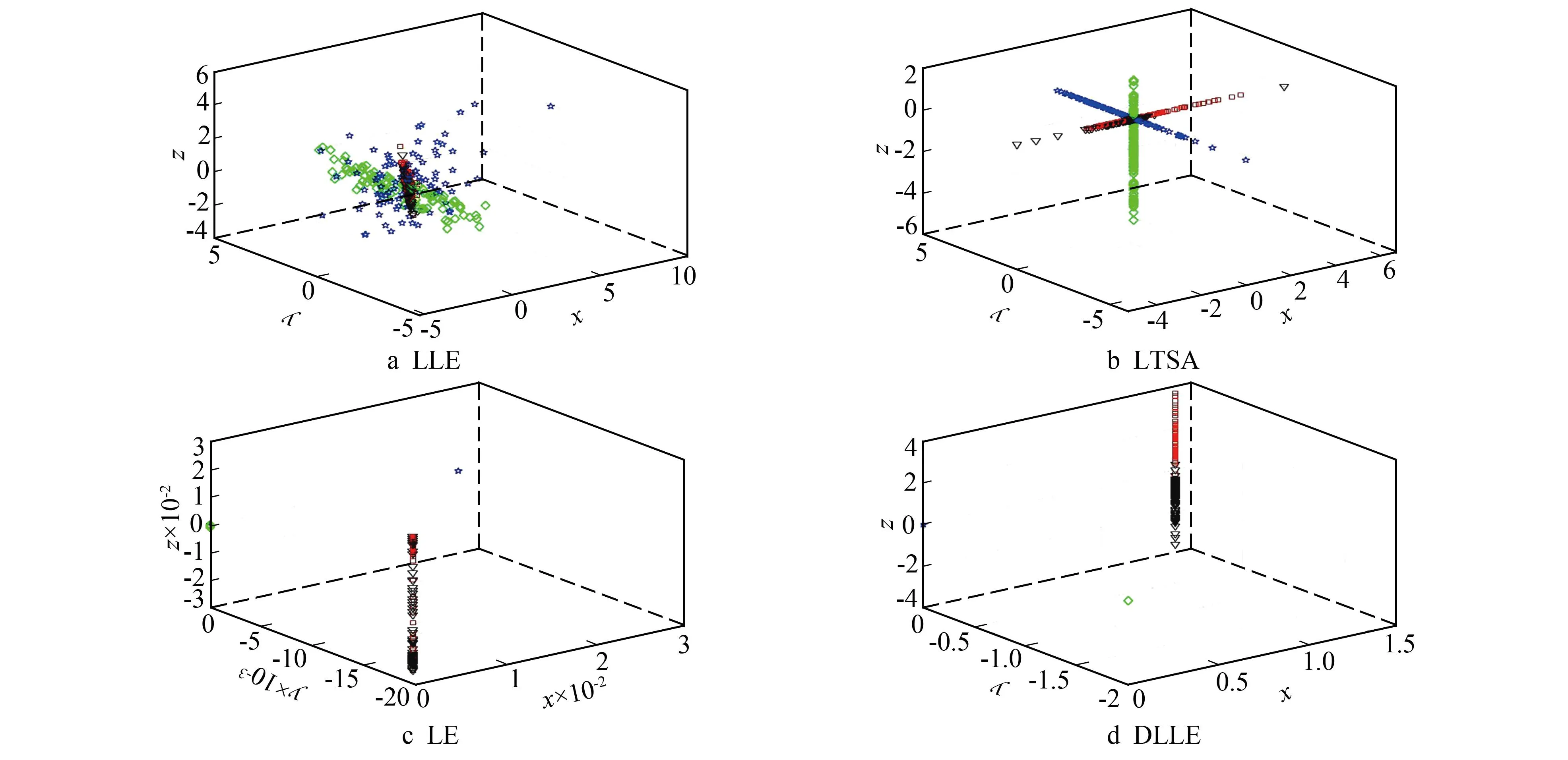
图5 不同降维算法处理千鹏数据结果

3.3 效果Fisher度量评估

Fisher度量是一种常用的数据聚类效果评估的方法,该方法通过利用类间距离Sb和类内距离Sw的商反应同一类数据的分散程度和不同类之间的分离程度,进一步评估不同降维算法的分类效果。

Fisher度量及相关参数Sb、Sw的具体求解公式如下:

(9)

在LLE、LTSA、局部保留投影算法LPP(Locality Preserving Projections)、LE和DLLE算法处理的两组数据的结果上使用Fisher度量计算公式,得到具体的相关参数Sb、Sw和F如表1、表2所示。

表1 不同算法对CWRU数据的Fisher度量的比较

表2 不同算法对千鹏数据的Fisher度量的比较

通过数据对比,可以观察到DLLE在5种降维算法中的表现,表1是不同算法对CWRU数据的Fisher度量的比较。其中类间距离中DLLE类间距离1.480 7,在5种降维算法中为最大值,表现出良好的分类效果能力,类内距离为0.774 9,相较LLE聚类效果提升明显,Fisher度量值1.910 7,除LPP算法Fisher度量值外最高。不同算法对千鹏数据的Fisher度量如表2所示。其中DLLE类间距离1.877 1在多种算法中仍为最大值,类内距离较小,Fisher度量值4.906 5为最大值。因此,DLLE的分类效果在5种算法中表现良好,有效提高了LLE的分类效果。

3.4 效果识别精度评估

分别在CWRU数据集和千鹏数据集上对多种不同算法的效果识别精度做评估,对每类样本80%进行训练,20%测试,结果如图5,图6所示。从图5,图6中可看出,在两组数据集上,DLLE算法在CWRU数据集上对4类样本的识别精度均较高,平均精度维持在91%左右,该算法在特征识别上具有较高精确度。

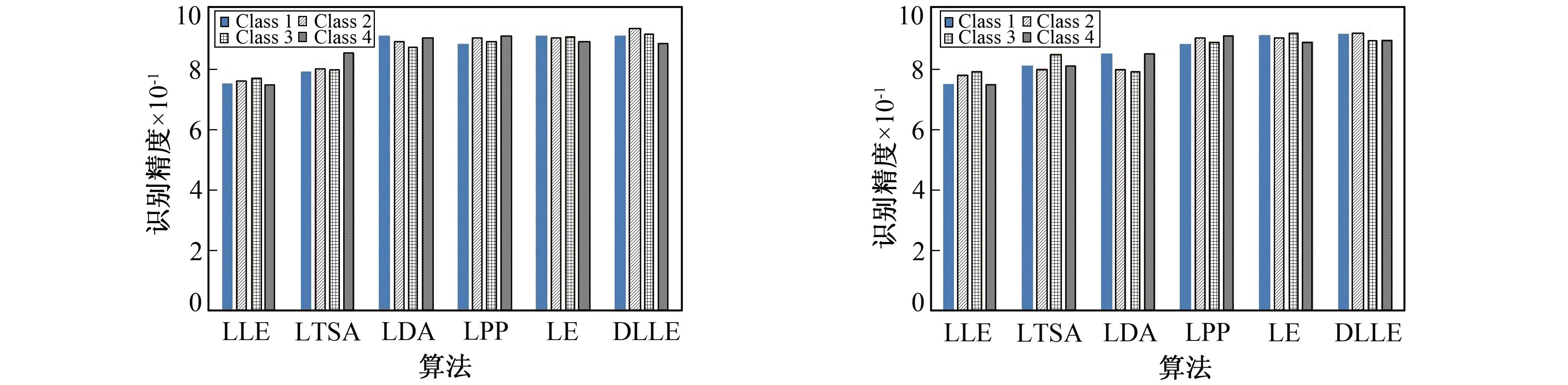
图6 CWRU数据集类别识别精度评估

4 结 语

为解决LLE算法难以充分挖掘高维电机轴承数据结构的问题,笔者提出了一种融合邻域分布属性的局部线性嵌入算法。该算法通过计算样本邻域分布之间的散度,对权重系数进行修正,实现了在低维空间中的数据保持高维空间中的邻域相似性关系。该算法在CWRU数据集和千鹏数据集上利用可视化、效果Fisher度量和效应识别精度对该算法进行评估。其中,在Fisher测量中,算法分别为1.910 7和4.906 5。在效果识别精度评价中,该算法保持了识别精度的91%左右,验证了该算法对轴承信号处理结果在可视化、分类和识别精度的优势。证明该算法对增强LLE算法挖掘电机轴承检测数据高维非线性结构具有一定意义。