基于BP神经网络和随机森林的煤中CO2饱和吸附量预测研究
侯 渊,高 飞
(1.山西省晋神能源有限公司,山西 忻州 036500;2.辽宁工程技术大学 安全科学与工程学院,辽宁 葫芦岛 125100)
CO2是造成全球气候变暖的主要温室气体。近年来,有学者提出将电厂烟气(体积分数16.5%CO2,79%N2,4.5%O2)注入煤矿的采空区,利用采空区遗煤对CO2的吸附实现碳封存的目的,这样不仅能节约从烟气中分离回收CO2的碳捕集成本,还能抑制采空区遗煤吸附O2自燃,即实现了灾害治理与节能减排的统一[1-2]。但是采空区物理化学环境复杂,影响煤层吸附CO2的因素有很多,这些因素不仅包括压力、温度、CO2体积分数等外部因素,还包括煤的孔隙结构、水分和矿物质等内部因素。因此,准确评估采空区遗煤对CO2的吸附能力对碳封存技术的有效实施具有指导意义。
目前,煤吸附CO2实验数据的拟合主要采用传统的理论模型:如Langmuir模型、D-A模型、D-R模型、BET模型等[3-5]。ARRIL等[6]曾在46℃下研究平衡湿度煤对CO2的等温吸附,发现利用扩展的Langmuir方程得到了很好的拟合效果。DUTTA等[7]在中压条件下比较了D-A模型和Langmuir模型对煤等温吸附CO2数据的拟合效果,结果表明,虽然两种模型都有良好的拟合效果,但D-A方程比Langmuir模型更为精确。传统的等温吸附模型虽然能准确解释实验数据,但理论模型仅适用于温度恒定、压力变化时煤对CO2吸附的研究,不同温度下模型的常数不同;所有的理论吸附模型都以各自的假设为前提,且目前为止没有一种理论模型能突破煤的种类限制,因此无法对煤在多重因素共同作用下的吸附行为进行研究。为了克服这些不足,MENG等[8]于2019年提出一种基于机器学习方法的创新吸附模型,该方法可以有效地预测某一类型煤的吸附行为,并且为了进一步突破煤炭类型的限制,提出了引入孔隙度、镜质组反射率等煤参数的第二种优化模型,可根据煤的基本物理化学参数预测煤的吸附行为。
1 实验数据来源与处理
参照前期的研究方法,采用控制变量法设计了144组实验,分别测试了3种煤在不同矿物质含量、含水率和CO2体积分数等条件下的CO2饱和吸附量,各变量的取值范围如表1所示,具体实验数据参考附录A[9-10]。将样本数据按照训练集与测试集8∶2的比例进行划分,即训练集116组,测试集28组。实验样本分别来自于新疆大南湖(DNH)煤矿、黑龙江峻德(JD)煤矿、山西同忻(TX)煤矿,吸附实验在常温常压条件下进行,矿物质含量的测定参考GB/T7560-2001。

表1 各特征参数的取值范围Table 1 The value range of characteristic parameters
2 BP神经网络模型
2.1 模型构建
2.1.1神经元个数
在本次研究中,选取比表面积、孔体积、平均孔径、矿物质含量、含水率和CO2体积分数6个影响因素作为模型的输入变量,因此模型输入层的神经元为6个,输出层的神经元为1个,即CO2饱和吸附量。节点数的选取对BP神经网络性能至关重要。节点数过高会导致过拟合现象,训练时间拉长;而节点太少会导致预测准确度降低。试凑法是一种常用方法,用于确定最佳的神经元个数[11]。这种方法首先根据经验公式确定隐含层的神经元个数,然后通过对不同神经元个数的网络进行训练比较,最终确定最佳的神经元个数[12]。经验公式如式(1)所示,其中隐藏层神经元个数在4~13之间为最佳选择,具体值的确定需要通过调整BP神经网络的参数以不断优化其网络结构。因此,过程中需要通过迭代次数和均方误差(MSE)来确定隐藏层的神经元个数。表2展示了不同神经元个数下的迭代次数和MSE值。
(1)
式中:α的范围为1~10;i为隐藏层的神经元个数;m为输入层的神经元个数;n为输出层的神经元个数。

表2 不同神经元个数对网络训练的影响Table 2 Effect of number of neurons on network training
由表2可知,随着隐藏层节点数的增加,迭代次数逐渐降低,当隐藏层节点数为12时,迭代次数最少,为27次。此时模型的网络误差EMS=1.79×10-4,模型最为精确。当隐藏层节点数大于12时,迭代次数和网络误差继续增大。因此本文选用的节点数为12个,并确定BP神经网络模型的结构为6-12-1,如图1所示。

图1 BP神经网络结构图Fig.1 Structure diagram of the BP neural network
2.1.2训练过程
在BP神经网络训练中,输入层和隐藏层之间使用tansig函数,预测模型采用purelin函数作为隐藏层到输出层的激活函数。选用具有较快训练速度和高模型精度的Levenberg-Marquardt BP算法作为BP神经网络预测模型训练方法。使用控制变量法经过多次实验后得出,最大迭代次数为1 000,最佳学习速率为0.01时,模型的泛化能力和训练效果最优。
2.2 结果分析
在MATLAB中建立上述BP神经网络预测模型,将输入输出数据及训练参数设置完成后进行仿真模拟计算,得到CO2饱和吸附量的预测值与实际值如图2所示。由图可以看出,测试集中,除了个别CO2饱和吸附量的预测值和实际值存在些许偏差,大多数CO2饱和吸附量预测值和实际值是非常接近的,几乎重合,这说明该BP神经网络预测模型是十分可靠的。对BP神经网络预测得到的结果进行分析,如表3所示,得到平均绝对误差为2.25%,平均相对误差为1.83%。其中,绝对误差大于5%的数据有2个,最大绝对误差为5.53%;相对误差均小于5%,最大相对误差为4.82%。计算得到测试数据的决定系数R2为0.994 6。

图2 BP神经网络测试集的预测值与实际值对比图Fig.2 Comparison between predicted and actual values of the BP neural network test set

表3 BP神经网络测试集的预测值与实际值Table 3 Predicted and actual values of the BP neural network test set
为检验模型的准确性,需要对模型进行评估。从统计学的角度来看,仅用一个性能指标进行评价是不够的。因此,采用平均绝对误差(EMA)、均方误差(EMS)及均方根误差(ERMS)3个性能指标对模型进行综合评估,使用公式(2)—(4)进行计算。经计算,BP神经网络的评价指标结果如表4所示,模型对训练数据和测试数据的精确度均较高。在测试集中,EMA和ERMS分别为0.022 5和0.071 8,均小于0.1,表明真实值与预测值之间的离散程度和偏差很小,预测结果符合预期要求。训练集与测试集的R2的差值为0.003 1,差异较小,说明模型很好地避免了过拟合现象的发生,具有一定的泛化能力。上述结果证明本研究提出的BP神经网络吸附预测模型可以很好地预测多因素条件下采空区煤层对CO2的饱和吸附量。
2组间LogMAR BCVA差异有统计学意义,年龄、性别比、SE及眼压差异均无统计学意义,见表1。与正常对照组比较,NAION组pRNFL厚度、RPC wiVD、ppVD均明显较低,差异均有统计学意义(均P<0.05),见表2;SCP血流密度、DCP血流密度及GCC厚度均明显较低,差异均有统计学意义(均P<0.05),而2组间pfVD差异无统计学意义,见表3。2组受检眼OCTA彩色血流密度图比较见图1。
(2)
(3)
(4)

表4 BP神经网络模型评价指标Table 4 Evaluation indicators of the BP neural network model

3 随机森林预测模型
在数据来源与处理的基础上,首先调用函数mapminmax将所有样本数据进行归一化处理。然后,为提高模型的预测精度,调取MATLAB中的随机森林模型进行多次测试。经过多次训练,设定决策树数目trees=100,最小叶子数leaf=2。通过随机森林模型计算得到的CO2饱和吸附量与实际值的对比图如图3所示。可以看出,测试集中有5个数据点的CO2饱和吸附量预测值和实际值存在较大偏差,其他CO2饱和吸附量的预测值和实际值非常接近。对随机森林模型预测得到的结果进行分析,如表5所示,平均绝对误差为3.20%,平均相对误差为2.74%。其中,绝对误差大于5%的数据有6个,最大绝对误差为9.90%;相对误差大于5%的数据有5个,最大相对误差为9.42%。计算得到测试数据的决定系数R2为0.986 5。

图3 随机森林测试集的预测值与实际值对比图Fig.3 Comparison between predicted and actual value of the random forest test set

表5 随机森林模型测试集的预测值与实际值Table 5 Predicted and actual values of the random forest model test set
同样,为检验随机森林模型的准确性,对模型进行评估。经计算随机森林模型的评价指标如表6所示,模型对训练数据和测试数据的精确度均较高。在训练集中,平均绝对误差和均方根误差分别为0.013 7和0.019 1;测试集中,平均绝对误差和均方根误差分别为0.032 0和0.090 5,均小于0.1。训练集和测试集的均方误差较为接近,模型的泛化能力较高。
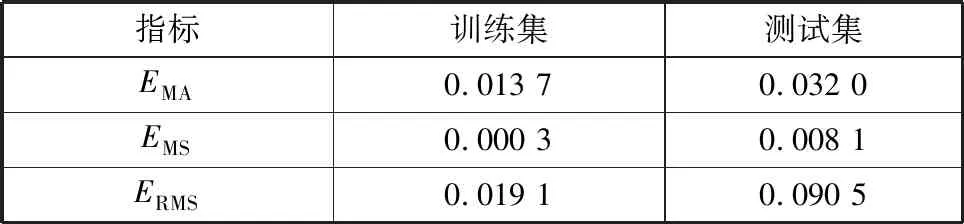
表6 随机森林模型的评价指标Table 6 Evaluation indicators of the random forest model
4 BP神经网络与随机森林模型对比分析
为进一步比较BP神经网络模型和随机森林模型的准确性,将两种模型对CO2饱和吸附量预测值的相对误差进行对比,如图4所示。可以看出,两种预测模型的相对误差均小于10%,都属于高精度的预测,证明两种模型都能对CO2的饱和吸附量进行预测。将两种预测模型的结果参数进行对比,如表7所示,发现BP神经网络模型的预测结果中,相对误差小于5%的数据为100%;而随机森林模型的预测结果中,相对误差小于5%的数据仅为82%。并且,BP神经网络预测模型的平均绝对误差为0.022 5,均方误差为0.005 1,均方根误差为0.071 8,3个指标均小于随机森林模型。上述对比说明BP神经网络模型在CO2饱和吸附量预测上的准确性更高,预测效果更好。模型的具体形式如式(5)所示。
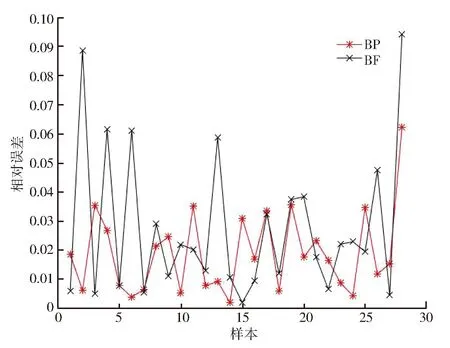
图4 两种模型预测值的误差对比图Fig.4 The error comparison of the predicted values of two models
Q(w1,w2,V,D,S,φ)=b0+
(5)
式中:Q为CO2饱和吸附量,cm3/g;w1为矿物质含量,%;w2为含水率,%;V为孔体积,cm3/g;D为孔径,nm;S为比表面积,m2/g;φ为初始CO2体积分数,%;w1,i,w2,i,w3,i,w4,i,w5,i,w6,i,分别为输入层到隐藏层各神经元间的连接权重,分别取0.028 9、-0.184 0、1.130 1、-0.537 8、0.226 0、-1.501 9;w7,i为隐藏层到输出层各神经元间的连接权重,取2.676 2;bi为输入层与隐藏层各神经元间的偏置,取-1.297 8;b0为隐藏层与输出层神经元间的偏置,取0.407 8。

表7 BP神经网络与随机森林的预测结果对比Table 7 Comparison of prediction results between the BP neural network and random forest
5 影响因素重要性排序
为探究各因素对煤吸附CO2的影响程度,本文采用基于MATLAB的特征变量重要性度量方法,评估决策树中决策节点特征使用的相对顺序。计算得到矿物质含量、含水率、孔径、孔体积、比表面积和CO2体积分数6个因素的重要度,并将重要度归一化,使其重要性权重之和为1,计算结果如图5所示。从图5可以看出,CO2体积分数是所有因素中影响程度最大的,约占总体的30%;其次是比表面积,约占26%。CO2体积分数、比表面积和含水率的重要性权重之和为75%,远高于其他3个因素。孔体积与平均孔径的影响程度较低,而矿物质含量的影响程度最小。分析原因是矿物质占据煤的孔隙后会抑制CO2的吸附,但一部分矿物质自身也能吸附微量的CO2,所以其对吸附量的总体影响最小。

图5 各因素重要性权重Fig.5 Importance weights of factors
6 结论
1)BP神经网络和随机森林模型均可以很好地预测煤对CO2的吸附能力,其中BP神经网络模型测试集的EMA和ERMS分别为0.022 5和0.071 8,随机森林模型测试集的EMA和ERMS分别为0.032 0和0.090 5,均小于0.1。
2)BP神经网络模型预测结果中相对误差小于5%的数据为100%,而随机森林模型预测结果中相对误差小于5%的数据为82%,且BP神经网络预测模型的平均绝对误差、均方误差和均方根误差均小于随机森林模型,证明BP神经网络在CO2饱和吸附量的预测应用上准确性更高,预测效果更好。
3)CO2体积分数是所有影响吸附的因素中影响程度最大的,约为30%;其次是比表面积,约为26%;CO2体积分数、比表面积和含水率3个因素的重要性权重之和可达75%,远高于其他3个因素;孔体积与平均孔径的影响程度较低,而矿物质含量对吸附量的影响不大。研究结果可为采空区封存CO2技术的应用提供理论支撑,对温室气体的减排具有重要意义。
附录A

表A1 3种煤在不同条件下的CO2饱和吸附量Table A1 CO2 saturation adsorption capacity of three types of coal under different conditions
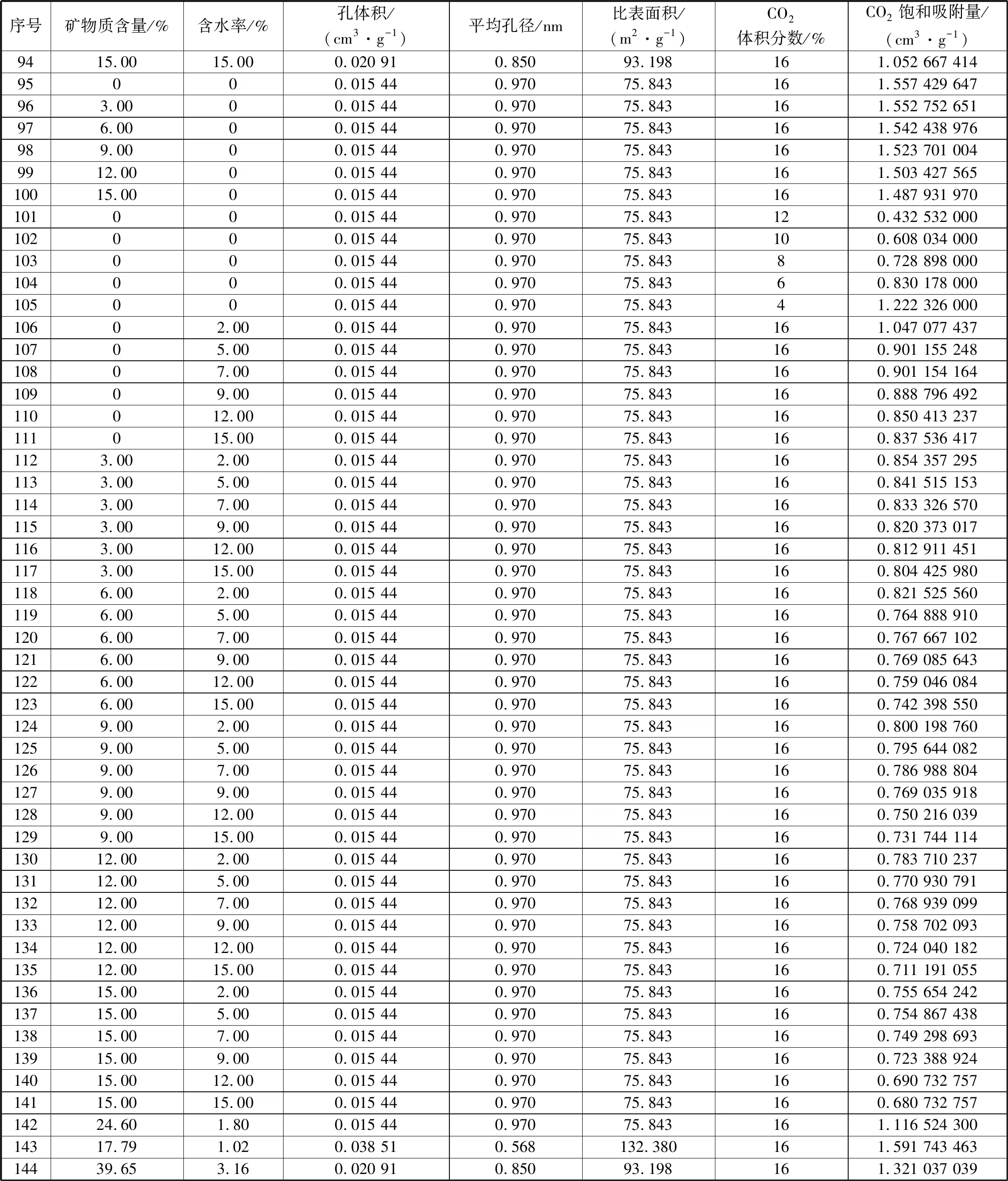
表A1(续)

