结构化视域下初中数学单元整体教学实践研究
王斌

摘要:以结构化视域为理论基础,以初中数学“图形的旋转”为研究对象,探讨了单元整体教学实践的有效性和可行性.通过对教学内容、教学方法、教学过程和教学评价等方面的分析,提出了一种基于结构化视域的初中数学单元整体教学模式,该教学模式可以有效提高学生的学习兴趣和学习效果,同时也符合教育教学的要求和实际需求.
关键词:结构化;初中数学;单元整体教学实践
新课程指出:“数学知识的教学,要把每堂课教学的知识置于整体知识体系中.”可见,结构化视域是一种较新的教育理论,它强调教学内容的结构化和整体化,注重学生的主动参与和自我发展.但在目前数学教学中还存在碎片化认知、浅层化理解和机械化训练等现象,基于新课标的落地,帮助教师更好地设计教学内容和教学方法,促进学生全面发展,进行大单元、结构化的教学亟待实现.为此,本研究以“图形的旋转”单元整体教学为例,以期为一线数学工作者和学生提供一些参考.
1 课前思考
1.1 设计思想
结构化视域认为,教学内容应该是有机的、系统的和整体的,而不是零散的、孤立的和无序的.教学方法应该是多样化的、灵活的和互动的,而不是单一的、死板的和机械的.教学过程应该是探究性的、合作性的和反思性的,而不是被动的、孤立的和机械的.教学评价应该是多元化的、综合性的和个性化的,而不是单一的、机械的和标准化的.“图形的旋转”是进一步学习图形全等及其有关性质的基础.本节将生活中的常见现象引入课堂,帮助学生获得理性认知,达成学习目标.[JP]
1.2 学习目标
(1)能例举说明生活中的各种旋转现象,培养善于观察以及概括总结的能力.
(2)完成对旋转从直观到抽象、感性到理性的认识,发展想象能力、分析与思辨能力.
(3)通过实验操作、知识应用等活动,数学的趣味性与实用性,提升分析运用、逻辑推理、归纳概括的学科素养.
2 教学过程
2.1 联系生活,引出新课
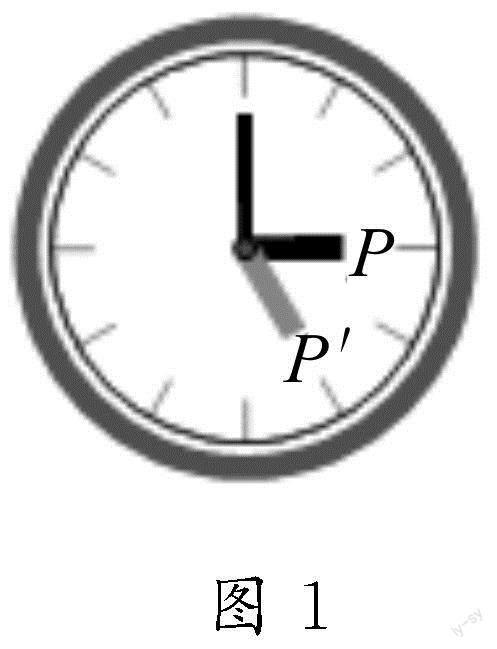
问题1 (1)如图1,观察钟表的指针,从位置P到P′指针做了什么运动?
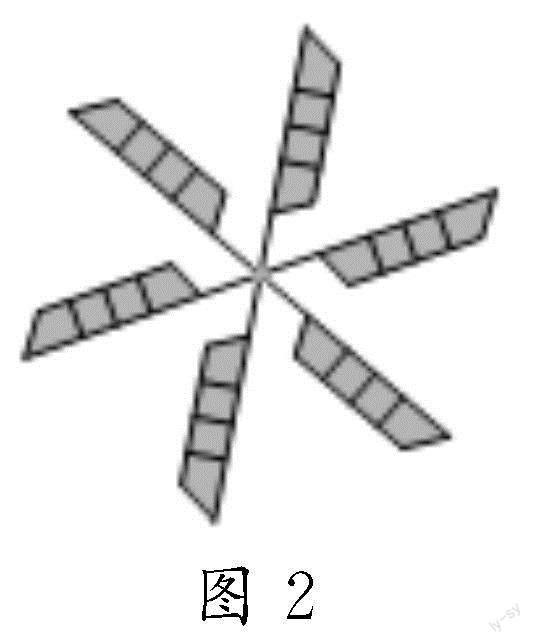
(2)如图2,观察风车,每个叶片至少转多少度能转到另一叶片的初始位置?
追问1:这些现象有哪些共同特点?
追问2:生活中还有哪些旋转现象呢?
追问3:对于河床水位逐月下降,插秧机的上下机械运动,跑步机传输带的运动,手表齿轮运动,顺时针拧螺丝,拧转保温瓶盖,哪些属于旋转运动.
教学关注:(1)教学前,要从学生已有知识经验出发,了解学生观察实例前的知识储备;(2)关注学生的概括能力,要求学生试着描述出旋转的定义;(3)列举丰富的生活实例,帮助学生判断区分不同物品的不同运动原理.
教学说明:学生或多或少有一定的生活中的旋转知识,所以能回答出实例中的共同特点.因此,要从学生最近发展区出发,从他们已有的知识经验中挖掘实例,帮助他们感受生活中的数学趣味性与实用性.
2.2 实验操作,探究新知
问题2 如图3,在纸板上剪出一个△ABC,再标记O作为旋转中心,然后将△ABC围绕O进行转动.
(1)你能画出旋转后的新三角形吗?
(2)△ABC与你画出的三角形是全等关系吗?为什么?
教学关注:学生自主完成操作练习,教师总结操作步骤,请学生小组合作归纳出图形旋转的特征.教学中要善于引导学生用所学知识解决问题.
教学说明:在自主、探究学习中,引导学生主动参与发现学习,培养学生勤于动手、动脑,善于观察、分析、交流、概括的实践能力.
2.3 新知应用,体会关联
问题3 如图4,在正方形ABCD的AD边上取一点E,连接CE,形成△CED.以點C为中心,把△CED顺时针旋转90°,得到△CBE′.
(1)画出△CBE′;
(2)求证:△CED≌△CBE′.
追问:第(2)问可以有多少种证法?
教学关注:(1)要求学生先观察后再动手画出图形,并运用旋转的基本特征说明作图的理论依据.(2)要求学生自主思考、分析、解答问题.(3)教师提前展示正方形的旋转.
教学说明:学以致用是学习的最高层次,教师要根据学生的能力设置问题,引领学生将与实际问题有关的知识内化到已有的认知结构中,在实践中促使其建构更丰富的数学知识体系.
2.4 巩固理解,类比化归
(1)一个小的三角形(图5)要形成图6的形状,需要怎样运动?
(2)一个菱形绕某一点旋转后得到图7.
①任意选择一个菱形,试着找出这个点,并用字母A标注出这点;
②所选菱形每次要旋转[CD#3]度,你是如何计算的?
教学说明:将所学知识进行拓展、应用,帮助学生理解概念、运用概念,从而加深对知识的理解.
2.5 归纳总结,知行合一
问题4 学习了本课,你知道平移、旋转有哪些共性或区别吗?
师生活动:根据单元整体知识体系,梳理出图形的平移、旋转的单元知识脉络.
教学说明:学习一个数学模型,要先厘清相关知识之间的关联,再从单元整体的视角出发,去建构知识脉络,达成目标结构的同生共长.
3 教学反思
3.1 关联生活,用数学眼光洞察世界
图形的平移与旋转的学习,是在已有知识经验的基础上,用数学的眼光洞察生活中的物体结构、特征、运动关系等[1].通过提出问题,引导学生思考和探究,帮助学生认识旋转,探索出旋转的基本性质.教师进一步追问学生“有哪些共同特点”“生活中还有哪些旋转现象”,在知识关联中帮助学生体会学习图形旋转的趣味性和必要性,促进学生在理解中学会数学思维,提升能力,发展素养.
3.2 关联能力,用思维建构知识体系
图形的旋转单元教学,在面对实际问题时,运用数学眼光,观察、思考旋转变换中各种点线所成的角以及各种相等的性质,有助于学生对知识结构的整体把握,借助多个旋转图形问题的拓展提升,梳理平移、旋转单元的整体知识脉络,帮助学生有效实现知识的迁移和创新.
3.3 关联应用,用数学眼光类比生成
数学教学要联系生活实际,要让学生知其然,也知其所以然.数学实验和问题是同一体,在课堂中将二者结合运用,更利于真实学习情境下的数学问题的解决.当然,课堂不能一味地关注实验而忽视问题的解决;反之,一节课也不能只是习题课,这样的课堂就与培养学生的核心素养背道而驰了[2].
关联应用,就是学生通过教材的学习,不断进行思维的创新与突破,学会用数学所特有的方式进行表达创新.学生在以“学为中心”的整合驱动中加工信息,获得理性认知,生成知识结构;在动脑、动口、动手中体验学科育人的价值,在引悟、感悟、顿悟中高效达成学习目标.
参考文献:
[1]何声清,綦春霞.数学项目式课程资源开发的理论与实践[J].中小学教师培训,2017(10):41-45.
[2]崔允漷.指向深度学习的学历案[J].人民教育,2017(20):43-48.

