面向调节阀的流量控制仿真研究

陈远，唐炜，程鲲鹏，刘新辉

(1．江苏科技大学机械工程学院，江苏镇江 212100；2．江苏远望仪器有限公司技术部，江苏泰州 225300)

0 前言

调节阀作为管网系统中的关键组成部分，在化工生产、油气开采等工业系统中应用广泛，其功能是接收控制信号调节流体通道面积，从而调节流场内介质流量。为了解决调节阀在流量控制场合应用时过于依赖流量测量装置、调节时间过长以及流量不稳定等问题，需要提升调节阀的流量控制性能，而良好的流量控制方法可以有效地提升管网系统中介质的传输效率、降低介质传输误差和延长阀门寿命。

国内外学者针对调节阀的研究主要集中在调节阀的结构优化和控制优化等方面。张萌[1]采用RBF-PID控制算法对电动调节阀进行了控制优化，有效改善了调节阀开度滞后的问题，但其过程控制模型依靠系统辨识工具得出，进行系统辨识时采用的数据有限，因此模型准确性不足；庄园等人[2]基于LabVIEW与MATLAB 联合编程，明显提升了模糊PID算法在调节阀流量控制系统中的运行效率，但该方法并未考虑阀门响应的快速性。HUANG等[3]针对调节阀调节过程中的流量稳定性问题进行了研究，提出了一种采用双线性插值算法的流量补偿器，有效改善了流量控制系统的动态特性，但该方法在调节开度时超调量较大，流量稳定时间较长。

综上所述，虽然现有研究各具优势，但总体仍存在实时性不足、模型准确度较低、调节速度较慢、超调量较大等缺点。针对此，本文作者基于Fluent仿真分析不同进出口压差、不同开度值下阀门内部流场的速度分布，汇总调节阀出口处的流速曲线，由此建立调节阀在不同压差和开度值下的出口流量三维数据表。控制调节阀开度是调节流量的关键，建立调节阀开度控制模型，同时完成模糊PID控制器的设计。结合上述的阀出口流量三维数据表、开度控制模型以及模糊PID控制器实现调节阀出口流量的实时控制。

1 流量控制原理

文中研究的调节阀尺寸较小，只考虑局部损失，假设阀出口通过的流量为Q，流体的平均流速为v，调节阀流道通流面积为S，流体的密度为ρ，阀两端压差为Δp，阀门流阻系数为ζ，则调节阀在某一开度下的流量计算可参考公式[4]：

(1)

可以看出：阀出口流量与阀两端压差成正比，与阀门流阻系数成反比。当调节阀进出口压力确定时，可通过调节开度改变调节阀流阻系数，进而调节流量。

调节阀流量控制流程如图1所示，首先通过压力传感器获取调节阀前后的管道进出口压力，将压差Δp与阀门当前开度值Vs发送至阀门开度控制器。开度控制器根据存储的表格插值计算得出当前通过阀的流量，与设定流量Qs进行比较后，若两者不同则需调整开度，查询数据库得出对应开度值Vn，之后选择模糊PID调节器形成流量闭环控制，进而控制调节阀开度直至达到目标开度值Vn。

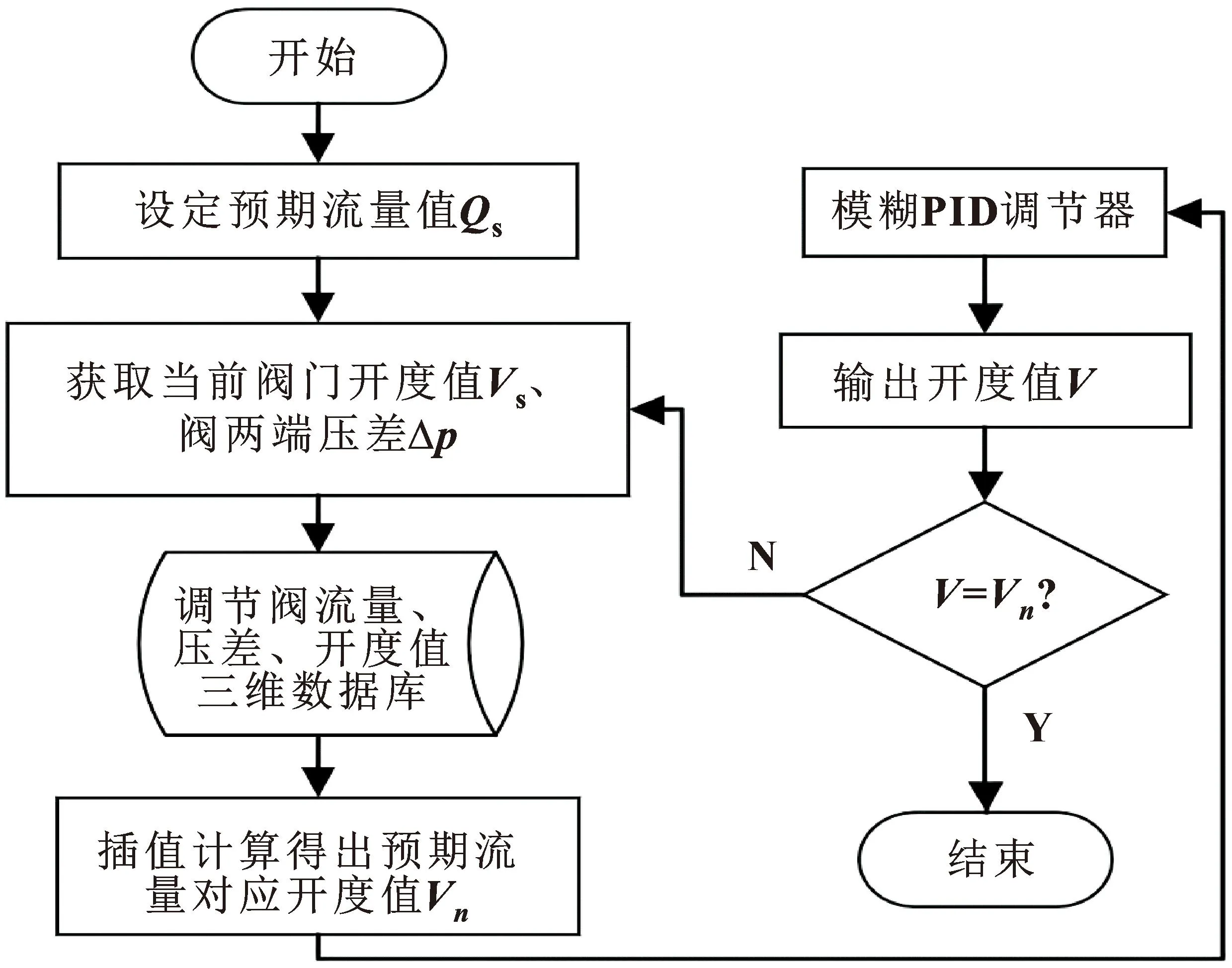
图1 调节阀流量控制流程

调节阀流量、压差、开度值三维数据库存储于调节阀开度控制器中，当调节阀的开度值和进出口的压差改变时，开度控制器可根据当前工况重新调节阀门的开度。

2 流量数值模拟

2.1 几何模型与网格划分

单座柱塞式调节阀如图2所示，主要包括阀座、阀体、阀芯和阀杆等零部件。调节阀公称压力为PN16，公称直径为40 mm，阀座直径为40 mm，阀杆最大行程为25 mm。

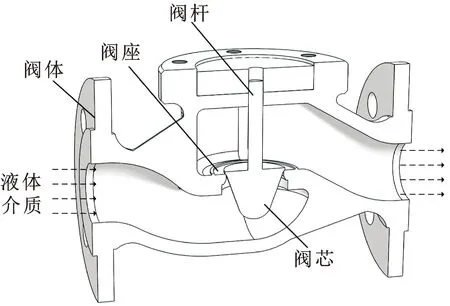
图2 调节阀模型

在SolidWorks三维建模软件中建立几何模型后导入到Fluent中，在调节阀入口延伸2倍直径的流场通道，在出口延伸6倍直径的流场通道，以保障调节阀两端流场的充分发展。

改变阀芯位置，通过反向运算得到阀门在不同开度值下的流道模型，将流道模型导入到Fluent Meshing进行网格划分。过去常用的四面体网格存在计算效率较低、离散精度低等不足；而多面体网格结构独特，对各种复杂模型都表现出了优良的适应力，同时还具备降低网格数量、提升数值模拟收敛速度的优势。综合考虑，在网格划分时选择了多面体网格[5]。流道模型的网格划分如图3所示。

图3 流道模型网格

将调节阀在全开状态下的模型划分网格后，采用质量流率这一指标进行网格无关性验证，其结果见表1。网格的数量由5.3×104增加至1.82×105，质量流率基本稳定，说明网格数量的影响可忽略。

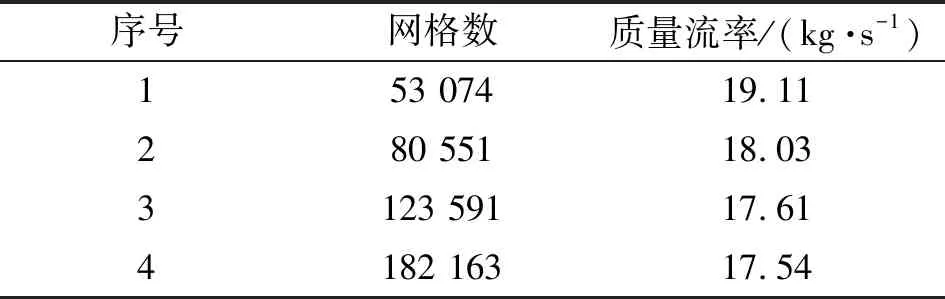
表1 网格无关性验证

2.2 数值模型

考虑到阀内流动的复杂性，设定阀内部介质为常温、不可压缩的水，且忽略介质的热量传递。为了保证阀内部的介质流动为湍流流动以及精确地模拟圆柱射流的传播，采用Realizableκ-ε湍流模型对阀内的流场进行稳态计算，压力速度耦合基于Coupled 求解算法，空间离散格式采用二阶迎风格式，湍流模型方程[6]如下：

(2)

(3)

式中：μ为水的流速；ρ为水的密度；Gκ、Gb分别表示由平均速度梯度和浮力引起的湍流动能。

2.3 阀口三维流量数据库建立

为了得出调节阀前后压差与阀出口流量的关系，将流道模型的入口条件和出口条件均设置为压力条件。调节阀具备保持出口压力的特性，保持出口压力为0.1 MPa，入口压力在0.3～1.1 MPa之间变化，则压差在0.2～1 MPa内变化。图4所示为阀门在50%开度、0.4 MPa压差下调节阀和前后管道的速度分布，在调节阀出口处设置多个速度散点，求出速度平均值，进而计算对应流量。

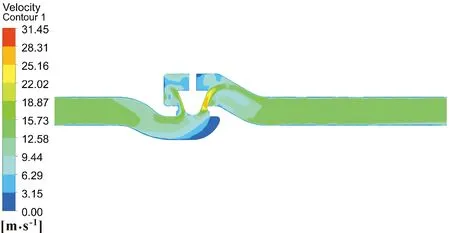
图4 0.4 MPa压差、50%开度时流场流速

按照此种方法进行大量仿真得出流量和开度、压差的三维数据图，如图5所示。可知：调节阀在0.2～1 MPa的进出口压差及10%～100%的开度过程中，调节阀出口流量在8.5～103.5 m3/h内变化。

3 调节阀开度控制模型

3.1 开度控制系统结构

调节阀控制系统由嵌入式控制器、调节阀驱动系统、数据处理单元、压力传感器等组成，如图6所示。在嵌入式开度控制器中设置预期流量后，开度控制器获取当前调节阀实际开度值Vs，通过压力传感器获取调节阀前后的压差Δp，基于CAN总线将数据发送至上位机，上位机再通过插值计算的方式从三维流量数据表中得出预期流量对应的阀门开度值Vn，通过CAN总线传输预期开度值Vn至开度控制器，由开度控制器输出开度信号至阀门驱动系统，从而控制阀门达到预期开度值Vn。

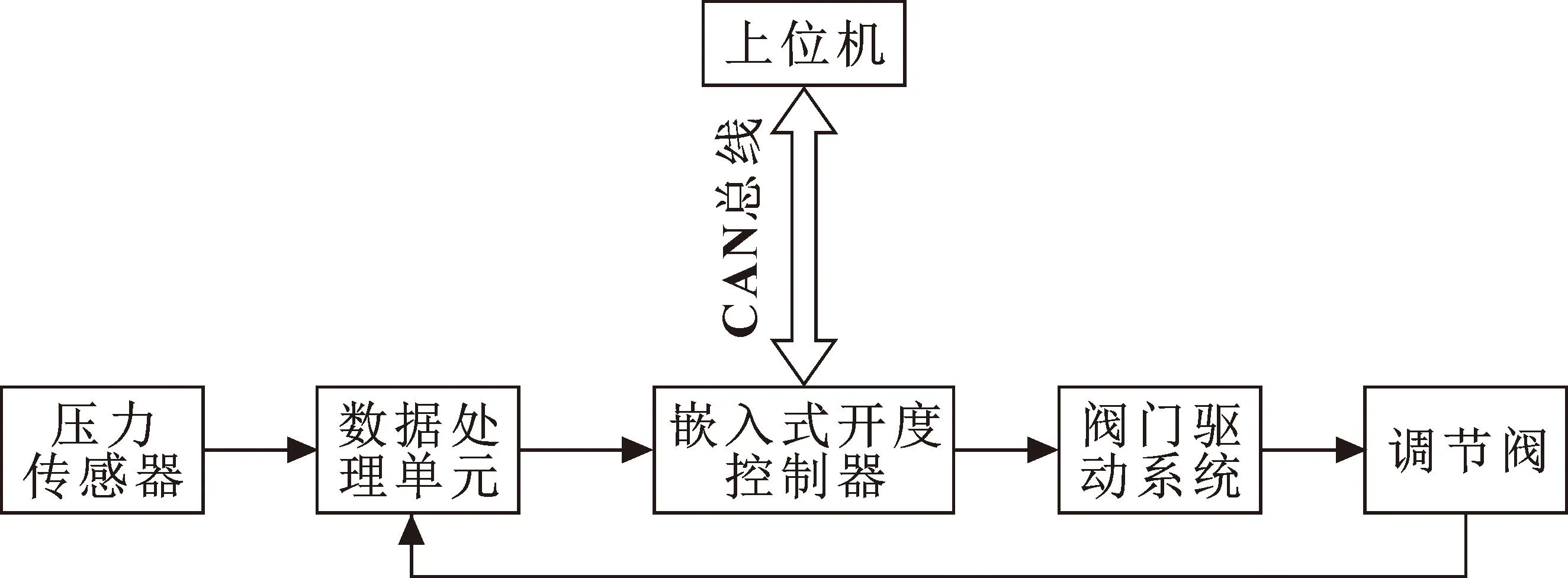
图6 调节阀控制系统结构

在调节阀的开度过程中，电机输出的转角位移经蜗轮蜗杆后，再由丝杠转化为直线位移作用在阀芯上，从而实现调节阀的开度控制。

调节阀开度控制系统的数学模型从以下几个部分进行建模：流量控制器、电动执行机构、传动装置。

3.1.1 流量控制器数学模型

调节阀的嵌入式控制器将开度信号经A/D转换后，再通过控制算法转化为控制电机的驱动信号，这一驱动过程可看作为一个比例环节与滞后环节的结合，其传递函数如下：

(4)

其中：Ud(s)为输出电压信号；Uc(s)为输入电压信号；Ks为控制器增益；Ts为控制器延迟。

嵌入式控制器的延迟很低，Ts可忽略，则控制器驱动环节可等效为

W(s)=Ks

(5)

3.1.2 执行机构数学模型

调节阀的执行机构采用直流伺服电机，电机输出转矩为式(6)：

Md(t)=KmId(t)

(6)

其中：Km为电机力矩系数；Id(t)为电枢电流。

电机转矩平衡表达式如式(7)：

(7)

式中：Md(t)为电机输出转矩；Mi(t)为负载力矩；w(t)为电机转速；Jm为电机转动惯量。

直流电机动态平衡方程如式(8)：

(8)

式中：Em(t)为感应电动势；Rα为定子电阻；Lα为定子电感。

联立式(6)—(8)可得式(9)：

(9)

式中：Ke为电机反电动势系数；f为摩擦因数。

在零初始条件下，通过拉氏变换能够得出传递函数[7]如下：

(10)

3.1.3 传动机构数学模型

直流伺服电机轴与蜗轮蜗杆相连，经蜗轮蜗杆减速的同时提高输出转矩。将它简化为一个比例环节，表达式如下：

(11)

式中：θ(s)为电机输出转角；θ1(s)为蜗轮输出转角；i为减速比。

丝杠的转角输出θ1和阀芯位移X具有以下关系：

(12)

将开度值V和阀芯位移X的比例关系代入式(12)，则可得到丝杠的转角输出θ1和调节阀开度值V的关系如下：

(13)

3.1.4 调节阀开度控制系统传递函数

将调节阀控制器环节、直流伺服电机和传动环节的传递函数合并后可得调节阀开度控制系统的传递函数为

(14)

调节阀开度控制系统主要参数如表2所示。

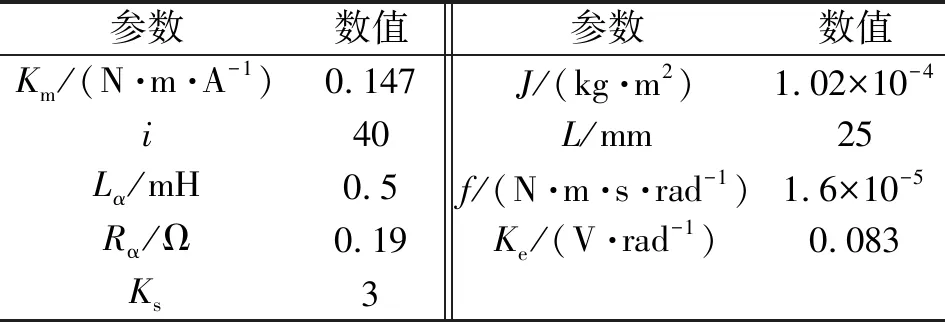
表2 开度控制系统主要参数

将以上参数代入式(14)，可得传递函数的具体表达式为

(15)

3.2 流量控制算法

在许多自动控制场合，PID控制算法具备普适性，以期望值和实际值的差值建立控制偏差，利用偏差的比例、微分、积分对控制对象进行控制。假设设定开度值与实际开度值偏差为e(k)，输出的实际开度值为U(k)，其离散化的表达形式为

e(k-1)]

(16)

其中：Kp、Kd、Ki分别为比例、微分、积分系数。

对于不同的压差、流量，常规PID设置的参数难以保证理想的开度控制效果，因此将模糊控制与常规PID结合解决此问题。模糊控制的主要特点是不依赖准确的数学模型，通过跟踪系统偏差动态调节PID参数，使控制效果更加出色。

模糊PID控制系统如图7所示。

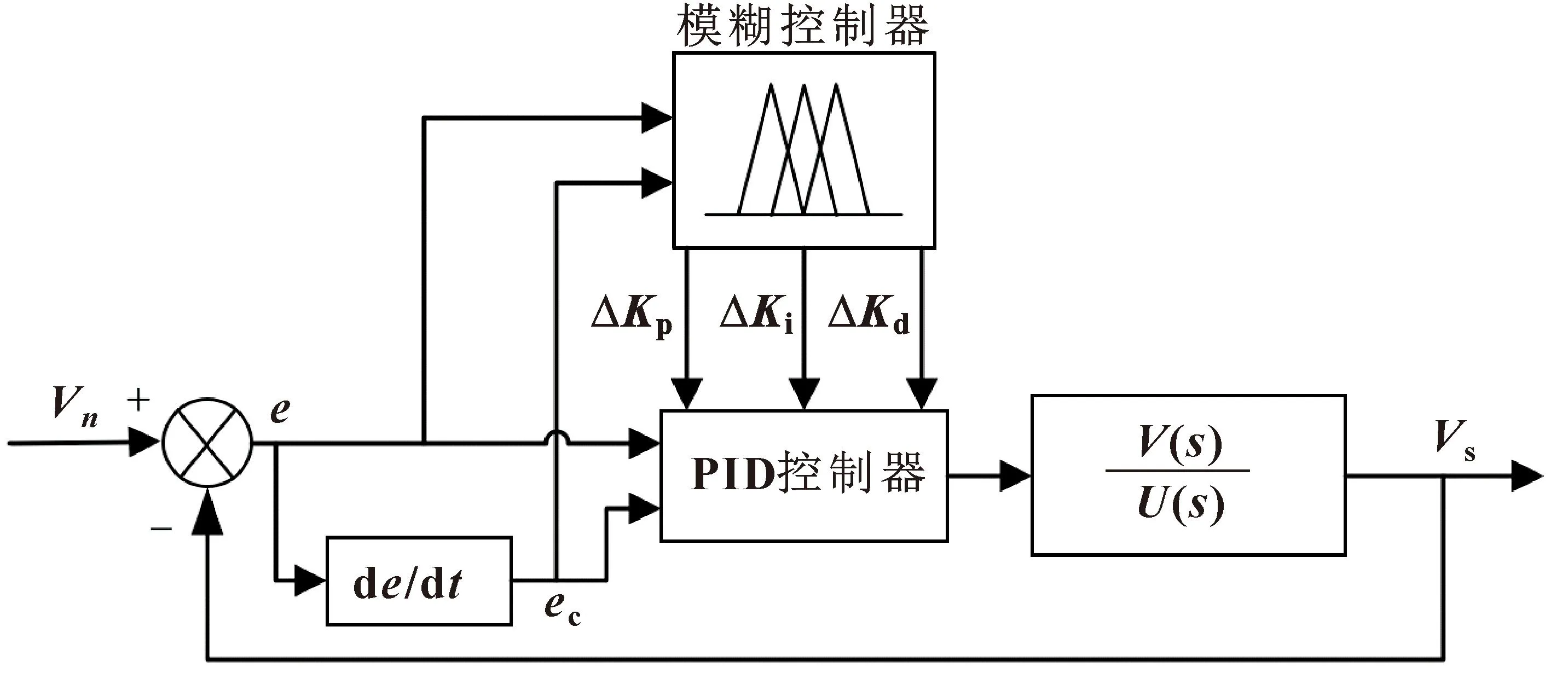
图7 模糊PID控制系统

在MATLAB 软件中建立模糊控制器，输入变量为开度值的偏差e和偏差变化率ec，将两者的范围量化为[-3，3]，把模糊论域表示成：{NB、NM、NS、ZO、PS、PM、PB}。隶属度函数可将集合映射到实数区间中，文中采用简单有效的三角形及高斯型隶属度函数。模糊控制的核心是建立合理的模糊规则表，文中建立了49条模糊规则[8]，如表3所示。

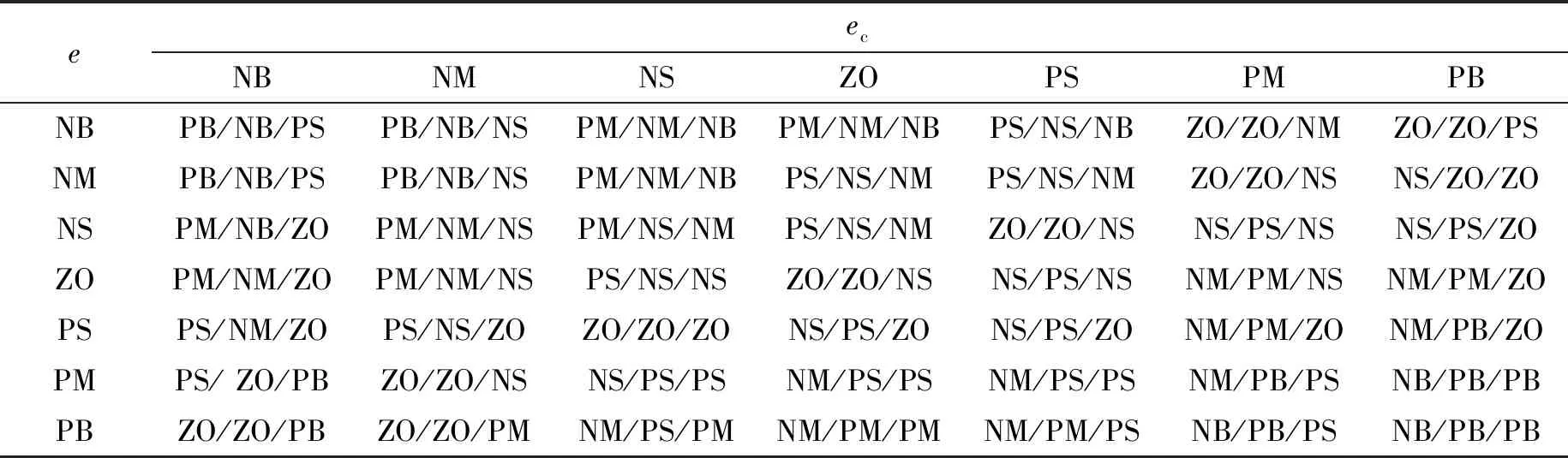
表 3 ΔKp、ΔKi、ΔKd模糊规则

4 仿真分析

为了对文中所提的流量控制系统进行验证，在仿真平台MATLAB/Simulink上进行仿真。针对开度控制系统搭建的仿真模型如图8所示。

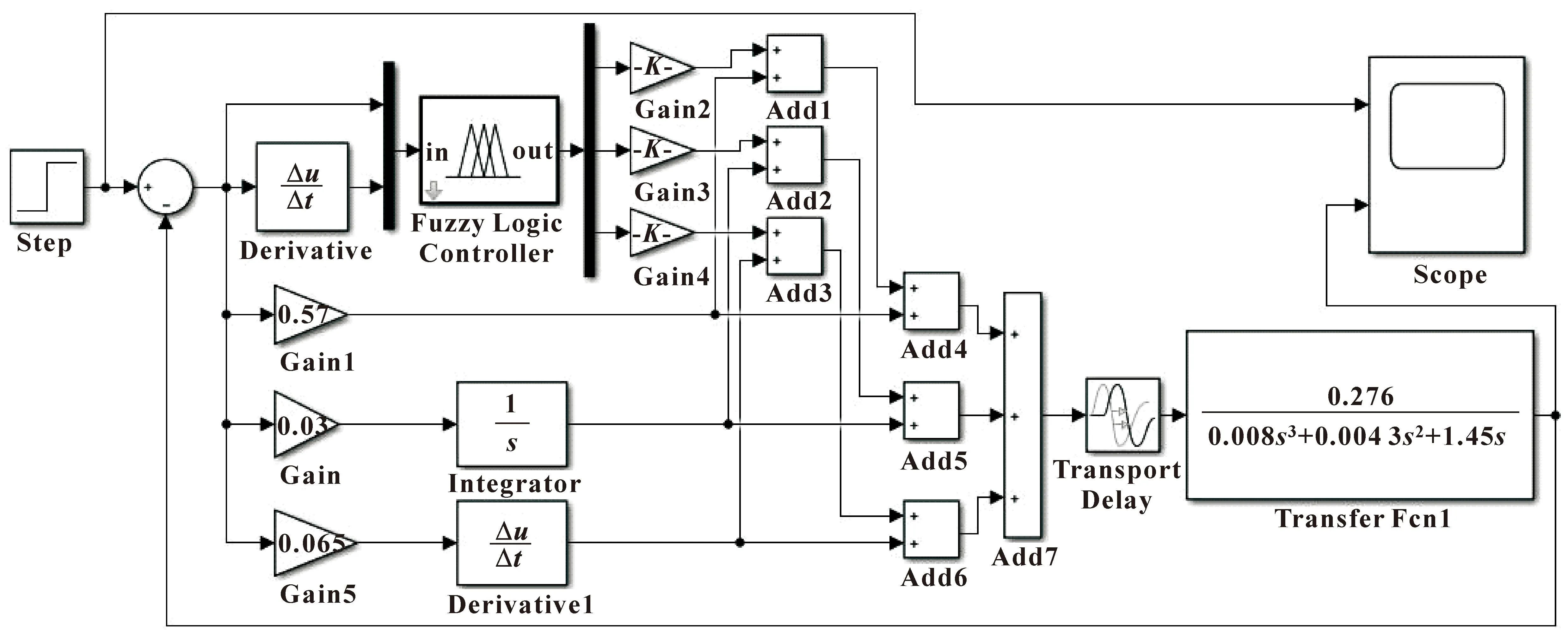
图8 Simulink仿真控制模型

调节阀出口流量设定完成后，当调节阀前后压差变化时，控制系统经过插值计算得出当前状态下所需的开度值，进而驱动阀门调节至此开度值。

首先对文中方法进行仿真分析，调节阀初始状态为：阀门全闭，阀进出口压差Δp为0.4 MPa，设置预期流量为59.4 m3/h。通过三维数据表插值计算得到初始状态下阀门需求开度为50%，则仿真系统的输入量设定为50%开度值的阶跃信号，设计的仿真试验主要模拟3个阶段的开度控制：(1)根据初始压差和设定流量控制调节阀达到预期开度值；(2)更新设定流量为63.5 m3/h，通过插值计算得出需要调节开度值至65%；(3)更新设定流量为66.8 m3/h，通过插值计算得出需要调节开度值至75%。

文献[9]与文献[10]也采用上述三阶段开度控制方案：将阀门开度设定为50%后依次调节至65%、75%。按文献[9]与文献[10]的模糊PID控制方法分别设置模糊规则、模糊论域以及隶属度函数，进而在MATLAB/Simulink上对两者建立的调节阀模型进行开度控制仿真。最终得到文中方法与文献[9]、文献[10]的仿真结果如图9所示。

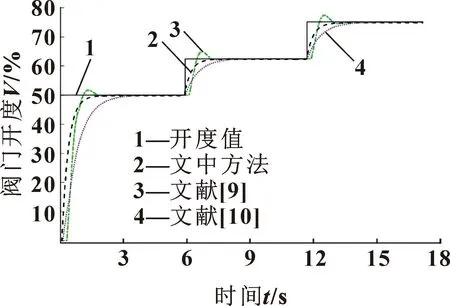
图9 阀门开度仿真结果

由图9可以看出：3种控制方法实现阀门开度跟踪的效果具有一些差异，在50%开度值的阶跃信号下，文献[9]的开度指令的响应时间为2.6 s，此方法响应较快，稳态性能较好，为时变、非线性的阀控系统提供了解决方案，但仍存在超调现象；文献[10]的开度指令响应时间为3.7 s，此方法响应较慢，但降低了响应曲线的超调量，控制效果良好；而文中的开度指令响应时间为1.8 s，与文献[9]、[10]对比，文中方法响应时间最快且消除了超调量，稳定状态更优，更易达到预设流量。

5 结论

文中针对调节阀展开仿真研究，基于Fluent仿真建立了调节阀出口流量与前后压差、开度值的三维数据库；将开度控制作为调节阀流量控制的关键点，基于调节阀开度控制系统建立了相应的数学模型，同时结合了模糊PID控制器，并采用MATLAB/Simulink仿真平台设计了三阶段的开度控制试验。结果表明：在调节阀出口流量三维数据库的基础上，结合调节阀开度控制数学模型与模糊PID控制策略进行开度控制，使得调节阀开度响应时间小于1.8 s，响应速度快，稳态误差小，最终使出口流量更易稳定在目标值，为解决调节阀在流量控制场合的应用中过于依赖流量测量装置、调节时间长、流量不稳定等问题提供了有效的解决方案。