基于IGWO 的台车轮注油系统注油量控制方法研究

李洪涛 ，库涛 ，王二林 ，刘金鑫，林乐新

(1.沈阳工业大学机械工程学院，辽宁沈阳 110870；2.中国科学院网络化控制系统重点实验室，辽宁沈阳 110016；3.中国科学院机器人与智能制造创新研究院，辽宁沈阳 110069；4.中国科学院沈阳自动化研究所，辽宁沈阳 110016；5.北京首钢股份有限公司，河北迁安 064404)

0 前言

烧结台车是烧结机的主要部件，在运行过程中始终伴随着烧结作业，因此烧结机台车轮不仅要承受行驶过程中弯道处的冲击，还要承受烧结矿的重力、高温[1]。恰当的注油可以有效降低烧结机台车轮工作温度，减少不必要的机械零件磨损，有效延长机械使用寿命，因此注油系统对于台车轮的有效工作十分重要。注油系统的注油量直接影响烧结机工作性能，若注油量过小会加大摩擦程度，甚至可能造成停机[2]；若注油量过大不仅会造成轴承温升加快[3]，还造成资源浪费。因此，注油系统注油量的智能控制是烧结机亟待解决的问题。

目前，对于注油系统常见的注油量控制方法有传统PID控制、内模控制、BP-PID控制等[4]。由于注油系统工作期间会受到较大的扰动，同时注油控制具有非线性和滞后性，传统PID控制存在控制精度低及鲁棒性差的问题，很难达到精确控制。内模控制需要对被控对象搭建精确的数学模型[5]，而注油控制系统构成较为复杂，传递函数计算困难，精确建模并不现实。传统BP神经网络的初始权值和阈值具有随机性，存在易陷入局部最优解和收敛速度慢等问题，影响算法的最终结果，需要借助其他优秀的算法与BP神经网络组合，得到稳定的初始权值和阈值。大量研究表明：灰狼算法较粒子群算法[6]、遗传算法[7]等大多数智能控制算法有更好的全局寻优能力。

为提高注油系统的注油精度，本文作者以某钢厂使用的烧结机为背景，提出一种基于改进灰狼算法的烧结机台车轮自动注油系统注油量智能控制方法。优化灰狼算法的收敛因子和权重系数，利用改进灰狼算法优秀的全局寻优能力优化BP神经网络，完成PID参数的自整定，以优化传统PID算法超调量大及BP-PID算法易陷入局部最优解的不足，实现注油量的精确控制。

1 自动注油系统注油量控制

根据某钢厂使用的360 m2烧结机设计了一款烧结机台车轮自动注油系统，主要由润滑模块、检测模块、注油执行模块等组成，如图1所示。

图1 台车轮自动注油系统组成

注油执行模块主要由工业机器人、浮动式加油枪等组成，用于跟踪台车轮的位置，并将润滑系统提供的润滑脂注入烧结机台车轮注油孔；检测模块主要由相机、传感器等组成，对台车轮进行识别、定位，并预测该车轮所需的注油量；润滑模块主要由压力传感器、电磁比例溢流阀、流量传感器等组成，输出实际所需的注油量，确保最终的注油。若注油量控制精度不到位，则无法满足台车轮的注油需求，影响其工作性能。

注油量控制结构如图2所示。使用传感器监控管路中的流量、压力等信息，并上传至PLC控制器，根据信息调整电液比例溢流阀的开度，改变管路中的压力。由于电控喷嘴处流量与管路中压力呈线性关系，进而通过控制电液比例溢流阀的开度实现控制注油量的目的。

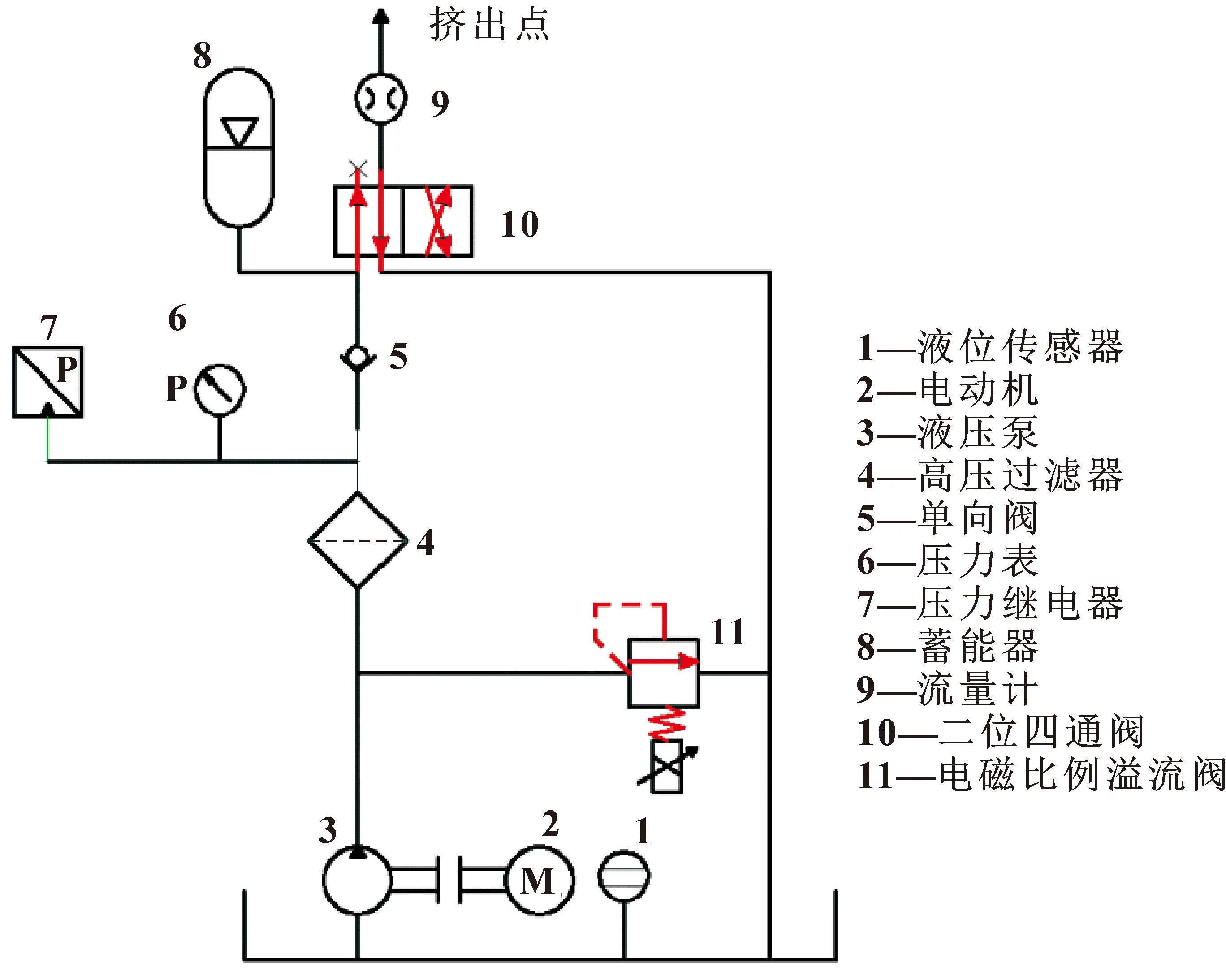
图2 注油量控制结构

2 注油量控制器设计

传统PID控制算法只能人工调整参数，对于注油量控制这类具有非线性特点的复杂系统控制性能较差。将具有自学习能力的BP神经网络与传统PID算法结合，对参数进行动态微调，可以很好地解决鲁棒性问题。但由于BP神经网络对权值过于依赖，易陷入局部最优解，影响最终控制结果。因此，采用改进灰狼算法对BP神经网络参数进行优化，其控制框图如图3所示。

图3 IGWO-BP神经网络PID控制框图

2.1 BP神经网络PID控制器设计

BP神经网络作为一种广泛使用的反馈网络，凭借其特性通过自学习能力可以拟合任意非线性函数[8]，将BP神经网络与传统PID算法相结合，通过对控制系统的不断学习，达到最优PID控制的需求。因此，BP神经网络PID控制器利用BP神经网络的自学习能力，实现PID控制器中Kp、Ki、Kd3个参数的自整定[9]。

增量式PID控制算法的数学公式如下：

u(k)=u(k-1)+Kp[e(k)-e(k-1)]+

Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)]

(1)

式中：u表示控制器输出；e表示系统实际输出y与真实值r的差值；k为采样次数。

BP神经网络主要由输入层、隐含层和输出层组成，根据增量式PID算法要求，设定BP神经网络的拓扑结构为4-5-3。将采样得到的rin(k)、yout(k)、e(k)、1作为神经网络输入，PID控制器的3个参数Kp、Ki、Kd作为输出，拓扑结构如图4所示。

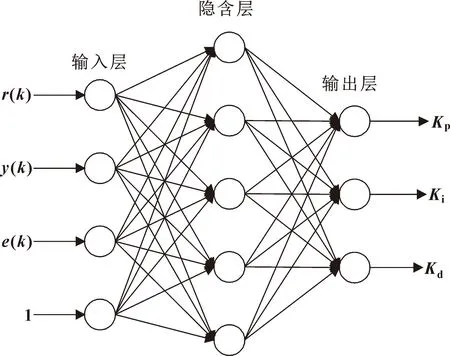
图4 BP神经网络结构

2.2 IGWO-BP神经网络PID控制器

2.2.1 灰狼优化算法

灰狼优化算法是由意大利学者MIRJALILI等[10]提出的一种新的元启发式算法，它通过模仿灰狼捕食猎物寻找最优解，具有参数少、易实现的优点[11]。

灰狼优化算法设计中将狼群按社会支配关系从高到低依次划分为α、β、δ、ω 4个等级，其中，每代种群中等级较高的3个解α、β、δ对优化过程进行引导，可以将算法分为包围、追捕、攻击3个阶段[12]。由于原始灰狼优化算法中既没有平衡全局搜索和局部搜索，也没有体现出狼群等级的优势，导致在搜寻过程中容易陷入局部最优，收敛速度慢，影响算法性能[13]。文中通过引入非线性收敛因子和动态权重策略对原始灰狼算法进行改进，帮助算法寻找全局最优解，提高算法收敛速度及精度。

2.2.2 灰狼算法的改进

2.2.2.1 非线性收敛因子策略

全局搜索能力与局部搜索能力的平衡是群智能优化算法的重要问题[14]。在原始灰狼优化算法中，收敛因子随着迭代次数从2到0线性递减，但实际迭代过程呈非线性分布，线性收敛因子无法平衡两者间的关系，影响算法的收敛速度。针对该问题，提出一种非线性收敛因子策略，计算公式如下：

(2)

式中：t为当前迭代次数；tmax为最大迭代次数；λ为衰减系数。

取最大迭代次数tmax为500，衰减系数λ为0.9，改进前后收敛因子对比如图5所示。可以看出：收敛因子a随着迭代次数的增加而非线性递减。在迭代初期，a的变化幅度平缓，提高全局搜索能力；迭代中后期a变化幅度加剧，加快算法收敛速度，提高搜索精度。因此，通过引入非线性收敛因子，实现了对算法全局搜索能力与局部搜索能力的平衡。

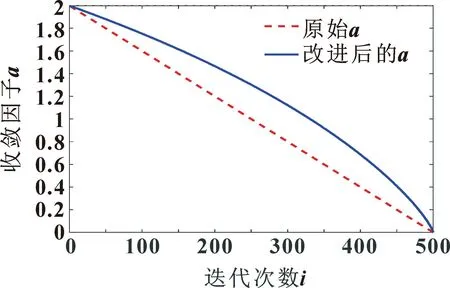
图5 收敛因子对比

2.2.2.2 动态权重策略

在原始灰狼算法中，α、β、δ狼对灰狼个体的引导权重相同，使得算法容易陷入局部最优，影响算法收敛速度[15]。针对该问题，通过引入高斯变异算子，提出一种基于适应的动态权重策略，数学模型如下：

(3)

X(t+1)=(w1X1+w2X2+w3X3)·

(1+a/2·N(0，1))

(4)

式中：w1、w2、w3分别为α、β、δ狼所占的权重；fα、fβ、fδ分别为α、β、δ狼的适应度值；a为式(2)得到的非线性收敛因子；N(0,1)为高斯分布；X(t+1)为灰狼当前回合的最终位置。

通过以上优化，在迭代初期，高斯变异算子可以提供给灰狼一个扰动，使得算法容易跳出局部最优解，优化全局搜索能力；在迭代中后期，扰动逐渐变小，加快算法收敛速度，稳定局部寻优能力，使得算法更好地寻找全局最优解，提高算法精度。

2.2.3 IGWO-BP神经网络PID控制器流程设计

根据以上研究，基于IGWO-BP-PID控制器主要由BP神经网络PID和IGWO 优化算法两部分组成。IGWO优化算法用于对BP神经网络的初始值及阈值进行寻优，进而动态输出PID的参数，其优化流程如图6所示。

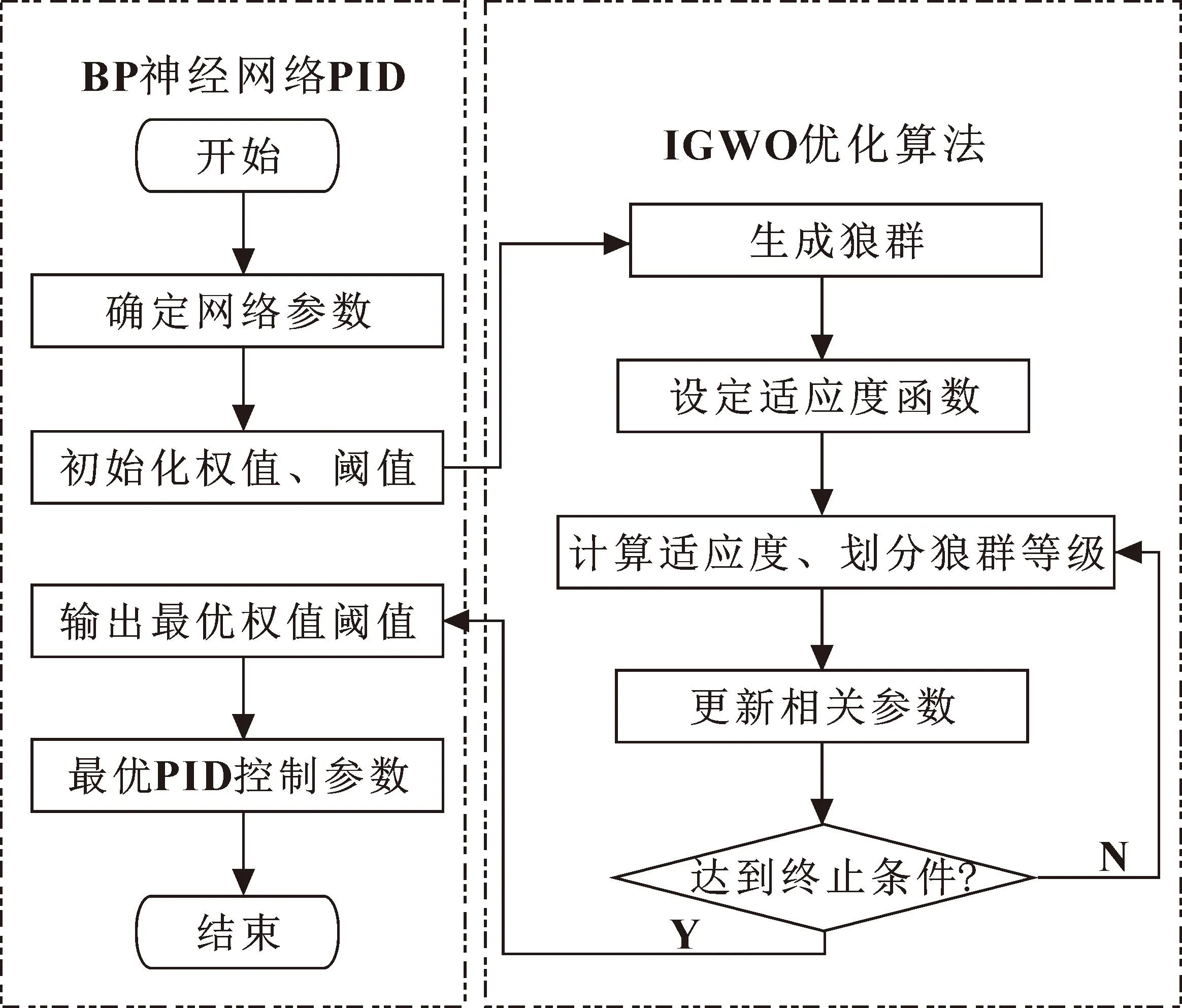
图6 IGWO-BP神经网络PID算法流程

3 实验仿真与分析

由于台车轮注油量控制系统中涉及电液比例溢流阀、二位四通阀、输油管道等环节，控制较为复杂，通过理论分析建立数学模型较为困难，因此采用试验测定方式确定数学模型，得到传递函数。文中通过系统辨识法，以管道压力p为操作变量、电控喷嘴处流量Q为被控对象，通过某注油系统提供的实验数据，利用MATLAB对该组数据辨识，得到控制系统传递函数如下：

(5)

根据得到的传递函数，利用MATLAB中的M函数及传统BP神经网络PID控制器进行仿真。注油量目标值设为rin并设定其值为40 mL，BP神经网络中惯性因子α=0.02，学习速率η=0.1，权重及阈值采用随机初始化的方式进行赋值，训练4次后系统输出响应曲线如图7所示。

图7 BP神经网络PID输出响应曲线

由图7可以看出：采用随机初始化的方式对BP神经网络PID进行训练，得到的控制效果不稳定，难以保证控制结果的稳定性。因此文中使用改进灰狼算法对BP神经网络的权值进行寻优，来提高控制性能。

将改进灰狼算法应用至BP神经网络PID控制器中，并与传统PID控制器及BP神经网络PID控制器的控制效果进行对比。其中传统PID控制器的参数为Kp=6.832、Ki=0.005 1 、Kd=8.594；IGWO算法中种群数量为30，最大迭代次数为50；BP神经网络中惯性因子α=0.02，学习速率η=0.1。

图8所示为引入改进灰狼算法寻优后适应度曲线，适应度在迭代25次后趋于稳定。经过IGWO算法优化后的BP-PID算法的相关参数Kp、Ki、Kd变化曲线如图 9所示。

由图9可以看出：经过IGWO算法优化后的BP神经网络能够对PID控制器参数实现快速整定，整定结果为Kp=0.679 635 、Ki=0.060 189 5 、Kd=0.857 869。同时，在4 s时添加幅值为41 mL的扰动信号，控制参数在短暂的波动后快速恢复稳定，表明算法有较强的鲁棒性。

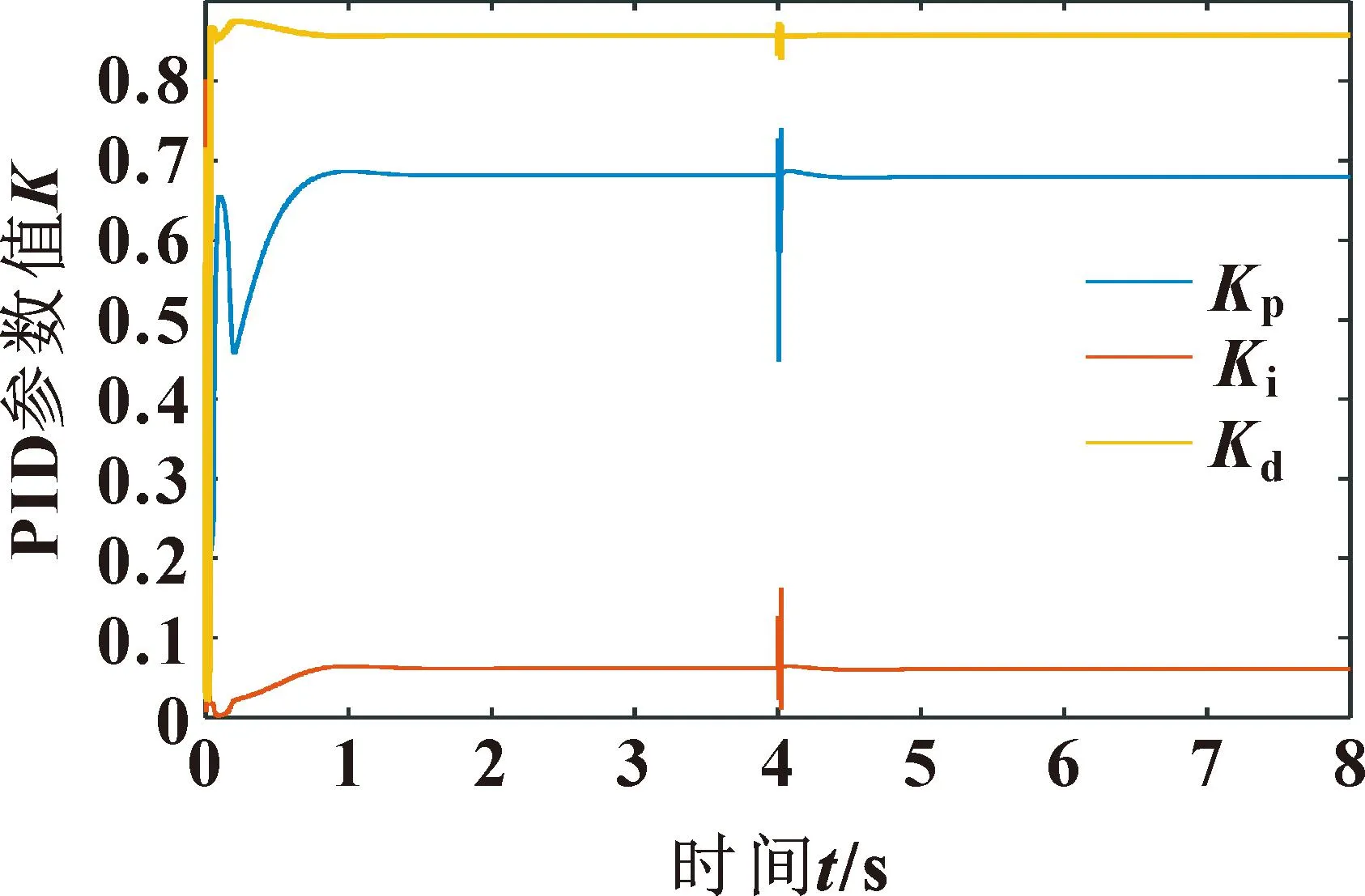
图9 IGWO-BP神经网络PID参数整定

各算法控制器相应信号下的响应曲线如图 10所示。

由图10可以看出：与传统PID控制器及BP神经网络PID控制器相比，IGWO-BP-PID控制器的超调量为2.13%，稳态误差为零，受到脉冲干扰后注油量幅度控制在±1 mL以内，且恢复稳定速度快，体现出良好的抗干扰能力。实验结果表明：文中提出的IGWO-BP-PID注油量控制方法能够满足烧结机润滑系统的控制性能要求。

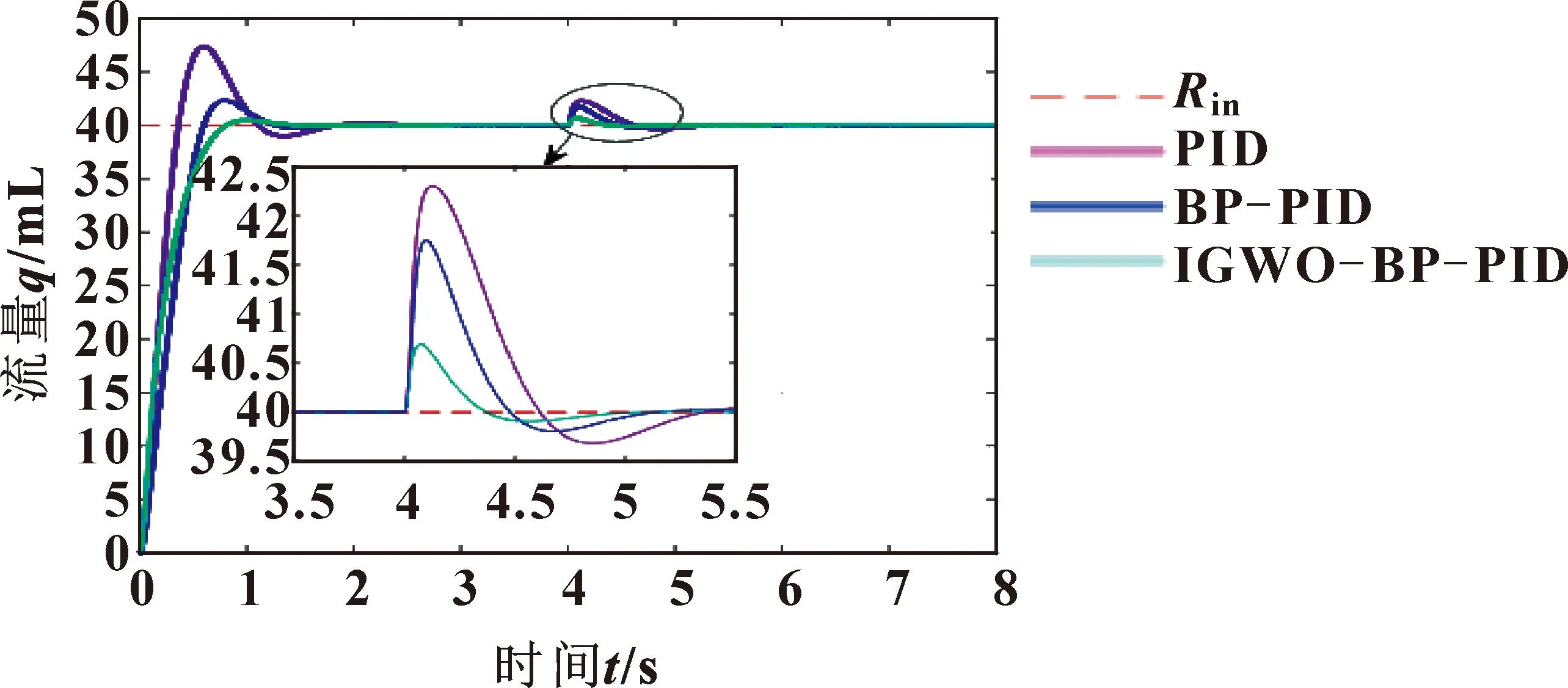
图10 不同控制器响应曲线

4 结束语

针对目前烧结机台车轮自动注油系统注油量控制算法的不足，提出一种基于IGWO的BP神经网络PID控制器，通过引入IGWO算法对BP神经网络进行优化，完成了PID参数自整定。研究结果表明：与传统PID控制器和BP-PID控制器相比，基于IGWO的BP神经网络PID控制器不仅超调量大幅度减小，且在面对扰动时也能快速收敛，具有较高的控制精度和良好的鲁棒性。