基于电阻元件定性效用分析的电路可稳定振荡性判定方法

于红兵，邹天乐

基于电阻元件定性效用分析的电路可稳定振荡性判定方法

于红兵1，邹天乐2

（1. 成都信息工程大学 通信工程学院，四川 成都 610225；2. 桂林理工大学 理学院，广西 桂林 541006）

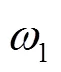
谐振选频环节；电阻；定性效用分析；可稳定振荡性

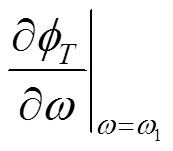
1 偏导关系的理论推导

1.1 谐振选频环节复参量的统一表达

一般而言，当电路以振荡器为目的进行设计时，电路中将含有选频环节．虽然它通常位于反馈网络中，但这只是习惯做法而已，理论上不应有这种限制．以LC振荡器为设计目的时，除三点式振荡器或Y型接法的新型三点式振荡器[4]523外，为达到选频功能的简便有效，通常选频环节的结构取为形式简单的RLC并联结构．但由于RLC串联结构与RLC并联结构存在对偶性，电路中引入RLC串联结构用作选频环节，在更具普遍意义的讨论中也应成为考察的对象[3]329．广义地讲，简便有效的RLC选频环节内部结构可取为RLC串联结构或RLC并联结构，本文将这两种情况统称为谐振选频环节．

当谐振选频环节为RLC串联结构时，此结构的阻抗为

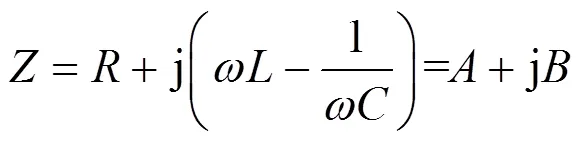
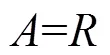
当谐振选频环节为RLC并联结构时，此结构的导纳为

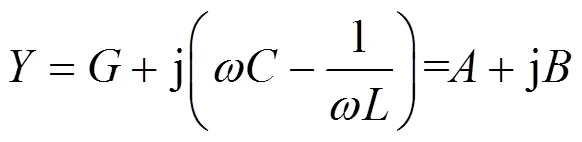
1.2 统一的偏导关系的推导

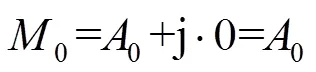
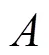
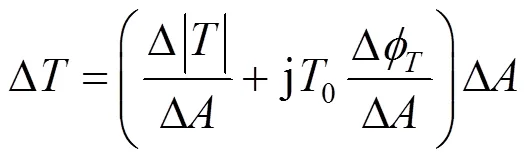
或写为

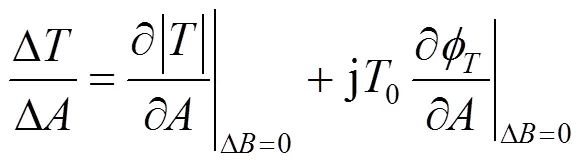
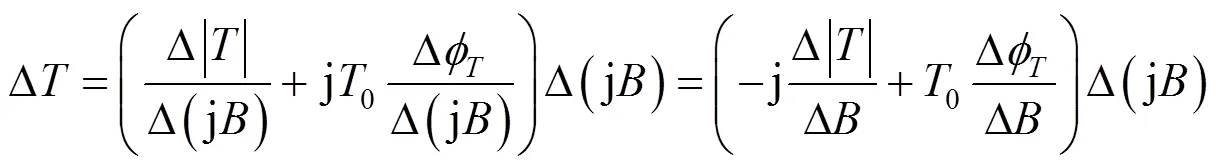
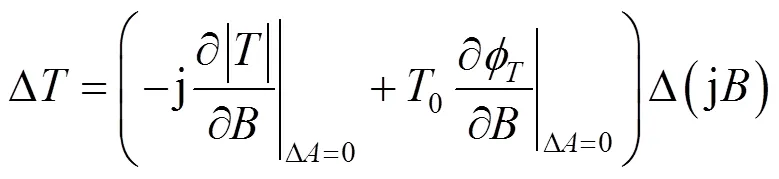
或写为

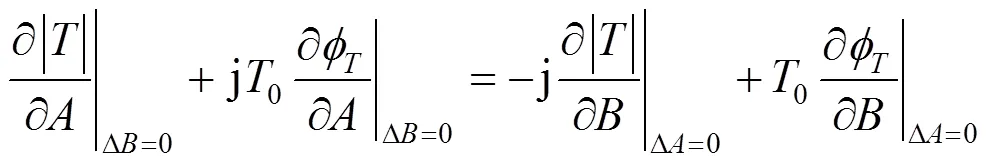
式（8）的实部与虚部分别写出，得到

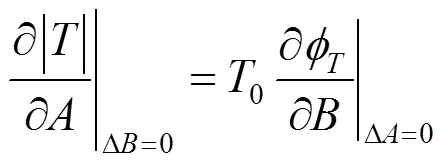
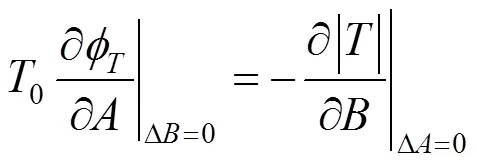
1.3 偏导关系的具体表达方式

当谐振选频环节为RLC串联结构时，此结构的复参量写为式（1），即

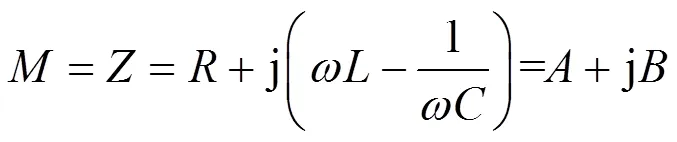
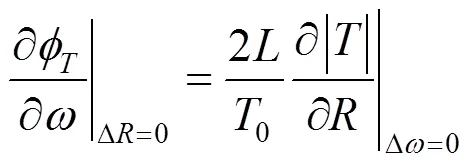
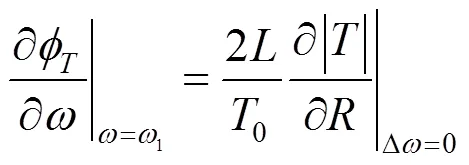
而当谐振选频环节为RLC并联结构时，此结构的复参量写为式（2），即

于是式（9）可具体表达为

2 判断偏导符号的定性方法

2.1 电路中谐振选频环节为RLC串联结构时的判断方法

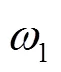
（2）对于这个因去掉了电抗元件而使信号流作用过程显得更加清晰的电路，进一步根据电路结构和元件参数的可能取值范围，判断电路有可能处于正反馈状态．

2.2 电路中谐振选频环节为RLC并联结构时的判断方法

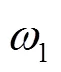
步骤（1）和步骤（2）与2.1节的步骤（1）和步骤（2）相同．

3 判断偏导符号的应用实例

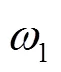
3.1 对文献[3]中图1电路的定性分析

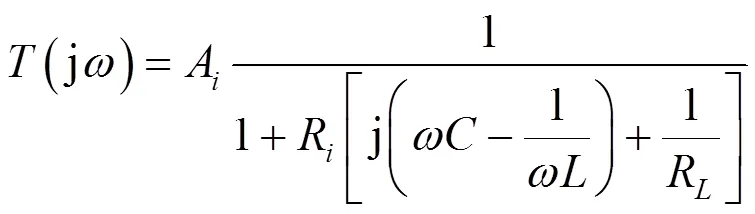
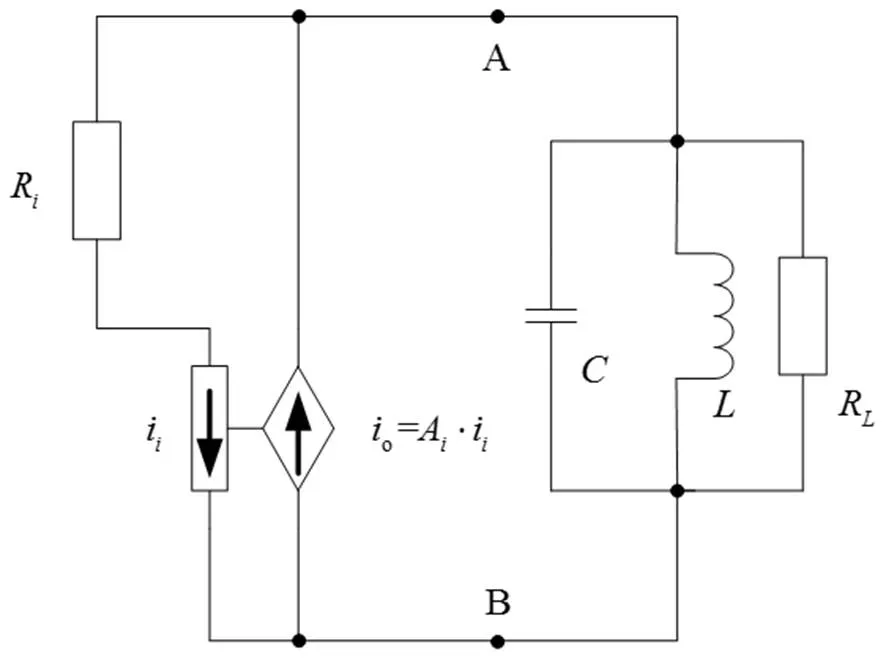
图1 文献[3]中图1所示电路

现在不考虑定量关系，由于电路中谐振选频环节为RLC并联结构，按本文2.2节所述方法，定性分析过程为：

因此环路增益会变小；

这一结论与直接按照定义出发计算，或应用象限法讨论的结果一致．

3.2 对文献[3]中图2电路的定性分析

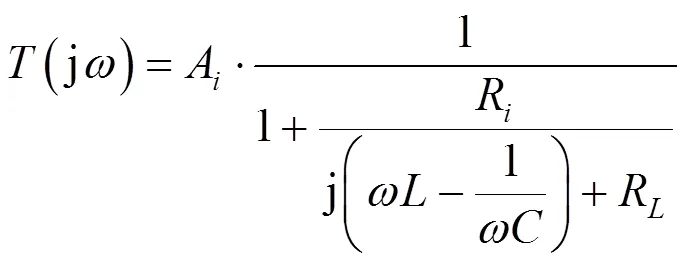
图2 文献[3]中图2所示电路

现在不考虑定量关系，由于电路中谐振选频环节为RLC串联结构，按本文2.1节所述方法，定性分析过程为：

因此环路增益会变大；

这一结论与应用象限法讨论的结果一致．

3.3 对文献[3]中图3所示电路的定性分析

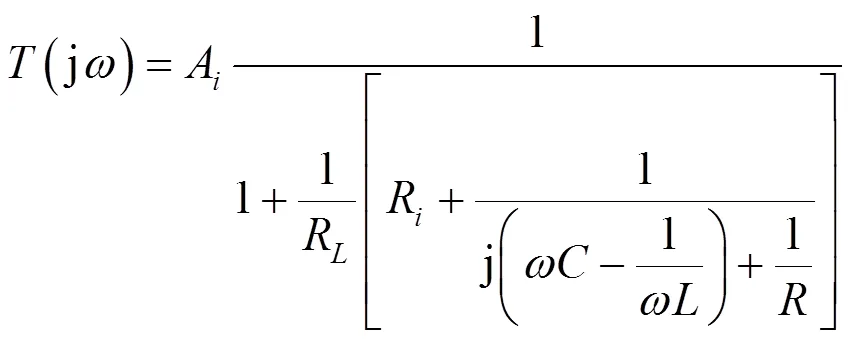
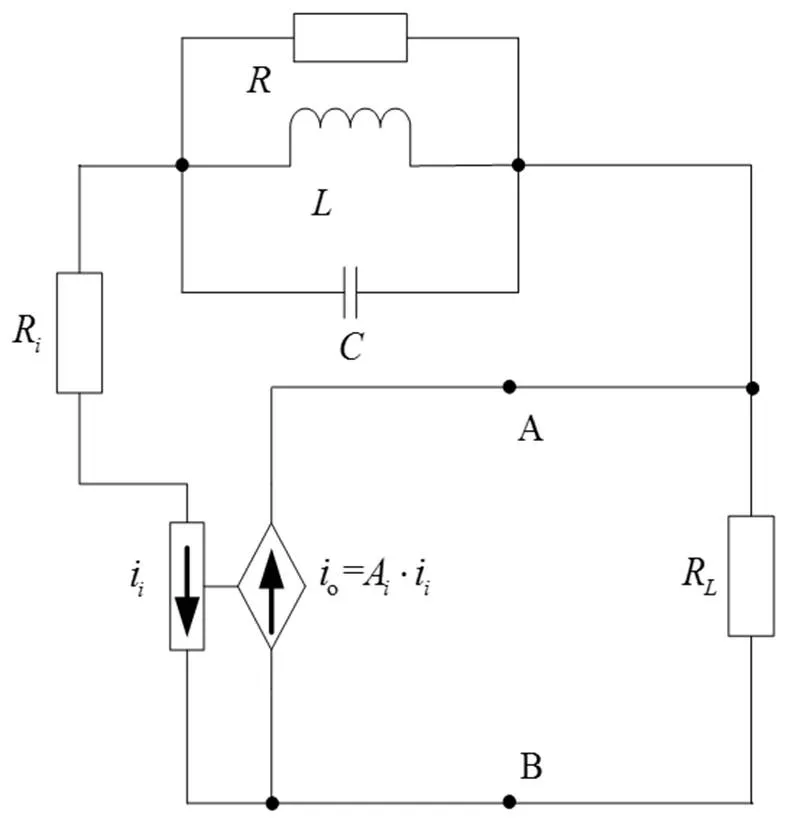
图3 文献[3]中图3所示电路

现在不考虑定量关系，由于电路中谐振选频环节为RLC并联结构，按本文2.2节所述方法，定性分析过程为：

因此环路增益会变大；

这一结论与应用象限法讨论的结果一致．

4 电路可稳定振荡性的一般判断方式

4.1 关于电路可稳定振荡性的分析方法

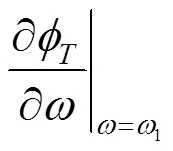
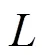
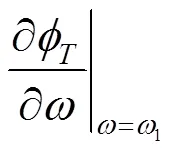
在LC振荡器电路（除三点式振荡器或Y型接法的新型三点式振荡器[4]523外）设计时，一般地可以将某一条支路取为RLC串联结构或RLC并联结构，使其成为谐振选频环节（RLC并联结构虽然内部有三条支路，但从对外连接特征上讲仍等同于单口网络或支路）．结论1有助于在振荡器设计时选取适当的谐振选频环节（串联结构或并联结构）．具体分析：

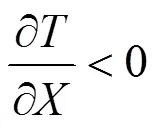
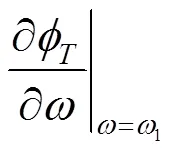
4.2 关于电路可振荡性的分析实例

图4 等效为非线性电阻的结构

这三个改变后的电路是否具备依赖于内稳幅的可稳定振荡性，可以分析：

5 电路可振荡性的实验内容总结

考虑对4.2节各个电路可稳定振荡性分析结论的仿真实验验证．

用仿真软件Multisim进行仿真实验时，为了对定量关系做出精确验证，并取得较大的元件参数变化范围，同时也为了排除次生现象的无谓干扰，可以直接用理想元件按图1～3的结构接成实验电路（然后再接入等效非线性电阻）进行仿真实验．由于这样的电路中不含直流源，为引入微小的扰动，可以在电路中接入适当的噪声源或微小的单脉冲源[3]329．

大量的仿真实验现象归纳为：

6 结语

[1] 于红兵．反馈型振荡器起振条件的新研究[J]．电子科技大学学报，2005，34（4）：573-576．

[2] 于红兵，王天宝．反馈型正弦波振荡器起振的元件参数分析[J]．四川师范大学学报（自然科学版），2005，28（6）：744-746．

[3] 于红兵，陈启兴，张金华．奇异振荡现象与多模振荡现象以及一类新型振荡器的研究[J]．电子器件，2013，36（3）：325-331．

[4] 于红兵，陈启兴．Y型接法的新型三点式振荡器的设计与研究[J]．电子器件，2012，35（5）：522-525．

[5] 于红兵．相移互补式振荡器[P]：中国，CN201610151657.7，2016-08-03．

[6] 于红兵，陈启兴．一种适用于小负载情况的振荡器[P]：中国，CN202011024731.1，2020-11-13．

[7] 于红兵，陈启兴．一种内含深负反馈结构的三极管振荡器[P]：中国，CN202210859690.0，2022-09-20．

[8] 谢嘉奎，宣月清，冯军．电子线路（非线性部分）[M]．北京：高等教育出版社，2000：116-123．

[9] 杨金法，彭虎．非线性电子线路[M]．北京：电子工业出版社，2003：60-63．

[10] 胡宴如，耿苏燕．高频电子线路[M]．北京：高等教育出版社，2015：81-88．

Determination method for potency of stable-oscillation based on qualitative effect analysis of resistor

YU Hongbing1，ZOU Tianle2

（1. School of Communication Engineering，Chengdu University of Information Technology，Chengdu 610225，China；2. School of Science， Guilin University of Technology，Guilin 541006，China）

resonant unit；resistor；qualitative effect analysis；potency of stable-oscillation

1007-9831（2023）11-0083-10

TN753.5∶G642.0

A

10.3969/j.issn.1007-9831.2023.11.017

2023-06-11

2022年度成都信息工程大学本科教育教学研究与改革项目（JYJG2022087）

于红兵（1965－)，男，山东文登人，副教授，硕士，从事电路理论与微波测量研究．E-mail：yhbyh@cuit.edu.cn