基于AHP 及模糊综合评价法的复杂城区铁路方案优选

刘明亮

(中铁第四勘察设计院集团有限公司,武汉 430063)

1 研究背景

随着我国城市建设的快速发展,铁路对城市客流的疏解作用越来越大,故需更多铁路引入城区并建立铁路枢纽,但复杂城区铁路选线受工程投资、城市规划、征地拆迁、线型条件等因素控制,往往需要研究多个方案进行多因素比选,特别是各方案均有利弊,难以决策出较优方案,迫切需要采用数学模型将各因素综合起来,科学评判最优方案[1-2]。 目前,已有学者开展相关研究,陈燕平提出基于不确定型决策方法的铁路方案优选[3];孙晓永提出一种基于层次分析法和熵权法的山区铁路选线研究[4];高康提出基于层次分析法对敦白高铁进行选线方法[5]。 但应用于复杂城区铁路选线的数学模型较少,以下基于AHP(层次分析法)及模糊综合评价法建立复杂城区铁路选线评价体系和决策模型[6-11],将铁路选线定量因素和定性因素综合起来,科学决策最优方案,并通过工程实例印证该方法的合理性,以期为复杂城区铁路选线决策提供借鉴。

2 模型构建

2.1 构建评价体系

基于AHP 及模糊综合评价法,将城区铁路线路方案比选作为目标层A,将工程投资B1、线型条件B2、征地拆迁B3、城市规划协调性B4、…、Bn等影响线路方案选择的主要因素作为准则层B,根据目标层所研究的线路方案作为方案层C,包含(方案C1、方案C2、方案C3、…、Cm等),根据以上条件,建立层次分析评价体系见图1。

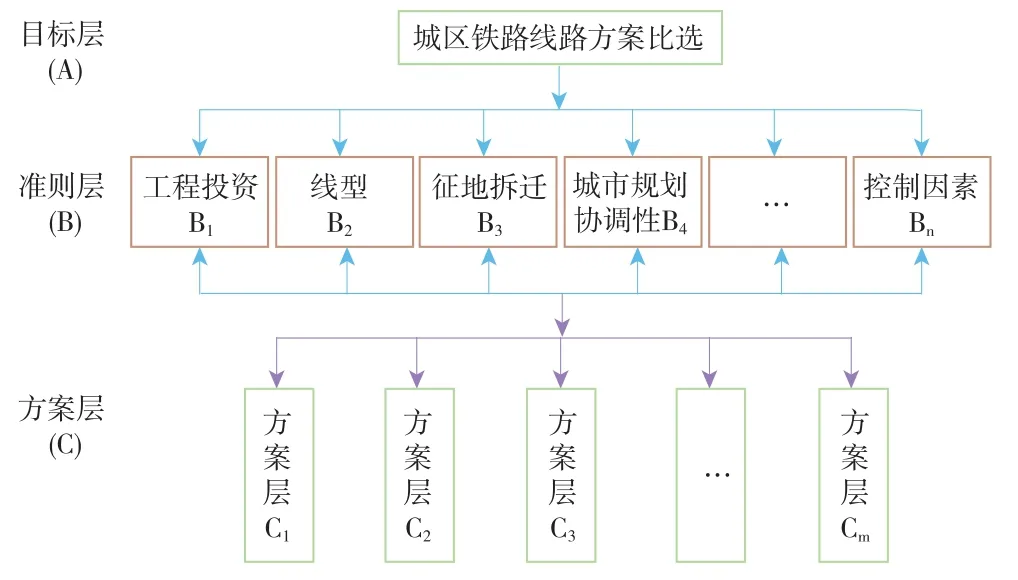
图1 层次分析评价体系

2.2 层次分析法计算权重

2.2.1 构造判断矩阵

设有n个主要因素B1,B2,…,Bn影响线路方案,两两比较其相对重要性,用aij表示因素和对线路方案选择的影响比,a=(aij)n×n为n×n的判断矩阵,即

其中,矩阵A中的元素满足aij>0,aii=1,aij=1/aji,i=1,2,…,n。 判断矩阵主对角线都为1,关于主对角线对称的元素互为倒数,所以判断矩阵为正互反矩阵。

关于i与j两因素相对权值的比值,采用Saaty 提出的1~9 标度法来确定aij值[12-13],具体对应关系见表1。

表1 Saaty 提出1~9 标度法含义

其中,2,4,6,8 分别介于1,3,5,7,9 对应的重要程度之间。

2.2.2 计算各因素权向量

各个因素对目标层(线路方案比选)的权向量,即为上述判断矩阵的最大特征值对应的特征向量,计算特征向量有多种方法[14],鉴于根法具有计算简便、精度高、且便于采用Matlab 编程化处理,拟采用根法计算权向量。

(1)A中每行因子连乘并开n次方,得到向量，其中

(2)对W∗作归一化处理,得到权重向量W=(w1,w2,…wn)T,其中

2.2.3 一致性检验

对于上述得出的各因素权值,需进行一致性检验,判断上述矩阵是否可以接受。

(1)对A中每列元素求和,得到向量s=(s1,s2,…,sn) ,其中

(2)计算最大特征根λmax的值

(3)根据最大特征根λmax计算一致性指标CI,CI=(λmax-n)/(n-1),与Saaty 的基准相比,计算一致性比率CR=CI/RI,一致性比率CR<0.1 满足一致性检验要求,RI采用的数值见表2。

表2 随机一致性指标RI 数值

2.3 模糊综合评价法

(1)首先需确定每个线路方案的主要因素集,即B={B1,B2,…,Bn},根据对各方案的优缺点分析,并结合专家意见,采用模糊综合评价法评价出对应每个因素的方案评价集V={V1,V2,…,Vp},并对评价集给予对应分值,得出模糊评价等级见表3。

表3 模糊评价等级

(2)按2.2 章节层次分析综合评判方法对方案层进行综合评判,得方案层对因素B1的权值向量=(u11,u12,…,u1m),将n个因素的层次评判结果综合起来,构成方案层对准则层的模糊隶属矩阵,即

(3)最后计算方案层对目标层的权向量,即=W×R=(ω1,ω2,…,ωm),权重最大者即为推荐方案。

3 工程实例

广珠(澳)高铁是提升粤港澳大湾区对外辐射能力,推进广佛极与珠澳极两极功能联动,支撑大湾区高水平建设的重大交通基础设施;是“八纵八横”高铁主通道京哈—京港澳通道的重要组成部分;是广珠(澳)客运主轴的高速城际客运通道[15],以下对广珠(澳)高铁广州城区帽峰山至鱼珠段方案进行比选。

(1)方案Ⅰ—鱼珠站址方案

线路自比较起点引出后向南,穿帽峰山至沙河镇,于广深铁路以南,黄埔体育馆以北设鱼珠站,出站后线路向东至比较终点,线路长度为34.7 km,桥隧比85.5%,本线至广深铁路上下行联络线长度合计4.113 km。

(2)方案Ⅱ—田螺山站址方案

线路自比较起点引出后折向南,穿帽峰山至罗岗儿童公园东侧上跨S117 省道,于广州石化东侧田螺山村设田螺山站,出站后线路继续向南至比较终点,线路长度29.223 km,桥隧比89.6%,本线至广深铁路上下行联络线长度合计15.628 km。

(3)方案Ⅲ—碧山站址方案

线路自比较起点引出后折向东南,穿帽峰山至黄坡新村东侧,于广汽本田东侧碧山村设碧山站,出站后线路上跨广深铁路至比较终点,线路长度为31.216 km,桥隧比87.9%,本线至广深铁路上下行联络下长度为8.536 km。

广珠(澳)高铁帽峰山至鱼珠段线路方案示意见图2。

3.1 AHP 法计算准则层权重

根据广珠(澳)高铁的功能定位,将工程投资B1、城市规划协调性B2、征地拆迁B3、线型条件B4等4 个影响线路方案主要因素作为准则层,根据多位专家意见,充分论证准则层各因素对目标层的相对重要程度,采用专家打分法,运用2.1.1 章节中所述的1~9 标度法构造准则层对方案层的判断矩阵。

经计算,求得判断矩阵的最大特征值和特征向量,并对特征向量进行归一化处理,得到准则层各主要因素对目标层的相对权重,其权向量为W= (0.052,0.583,0.251,0.115) ,根据最大特征根λmax计算一致性指标,CI=0.053,CR=0.059<0.1,满足一致性检验要求。

3.2 模糊综合评价方案结果

从工程投资方面分析,方案Ⅰ联络线较方案Ⅱ展短11.515 km,较方案Ⅲ短4.423 km,且拆迁分别减少7.89,5.59 万m2,综合工程投资最省。

从对城市规划的影响方面分析,方案Ⅰ鱼珠站位于广州第二CBD 等商业区,对周边带动作用强,而方案Ⅱ夹于广州石化与广深高速之间,周边空间有限,对城市规划影响大,方案Ⅲ-东侧紧邻西侧靠近广汽本田,周边可利用土地极少,综合开发十分有限。

从征地拆迁角度分析,方案Ⅰ拆迁主要为小型商业厂房,拆迁房屋总体可控,方案Ⅱ正穿佳都智慧城市产业基地、科学城净化厂等大型企业;方案Ⅲ线路正穿名美科技产业园、中马科学园等多个大型企业,拆迁协调难度极大。

从线型条件方面分析,方案Ⅰ-限速长度约7.8 km,方案Ⅱ平纵断面条件满足350 km/h 条件,方案Ⅲ限速长度约3.4 km。

经分析,主要因素集为B={B1,B2,B3,B4},根据上述对各方案的优缺点分析,构造模糊评价集V={明显好,好,稍好,稍差,差},结合多位专家评判意见,采用模糊综合评价法得出评价等级对应的分值,见表5。

表5 模糊评价等级分值

根据优缺点分析,并采用专家打分平均法,再结合表5 中模糊评价等级得出方案层对准则层的模糊评价结果,见表6。

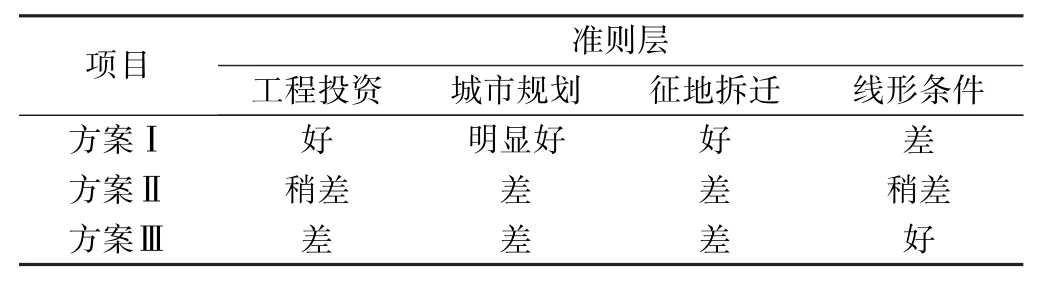
表6 方案层模糊评价

对每个主要因素按层次分析评判方法对方案层进行综合评判,得方案层对主要因素的权值向量,将4 个因素的层次评判结果综合起来,构成方案层对准则层的模糊隶属矩阵如下。

计算方案层对目标层的权向量:=W×R=(0.430,0.292,0.278),根据模糊评价结果,方案Ⅰ对应的权重大,故选择方案Ⅰ作为推荐方案,这与最终可研推荐的方案保持一致,说明基于AHP 及模糊综合评价法对线路方案评价科学合理。

4 结论

对于城区铁路选线决策的难点,基于层次分析法和模糊综合评价法建立城区铁路选线决策体系,将方案的各项指标定量化,科学评价各方案的优劣,最终确定推荐方案,并将决策方案运用于广珠(澳)高铁帽峰山至鱼珠段线路方案比选的具体工程中,通过决策模型评价得出如下结论。

(1)AHP 和模糊综合评价法理论构架简单,科学合理,适合复杂城区铁路选线比选时采用。

(2)城区铁路控制因素多,线路复杂,通过两个模型的综合运用可以避免仅靠定性分析的主观性和定量分析的局限性,解决了仅靠经验难以决策的问题。

(3)通过AHP 和模糊综合评价法的计算,代入工程实践,得出广珠(澳)高铁帽峰山至鱼珠段线路的推荐方案,该方案与可研推荐方案一致,印证了AHP 和模糊综合评价法的合理性。