预测城市河流污染物浓度的对流扩散模型

孙景琛

（山西开放大学,山西 太原 030027）

1 河流概况

实验河流里韦林河位于英格兰东北部谢菲尔德市西北部。实验地区位于是里韦林河的下游地区。平均降雨量为每年834.6 mm。实验场地西南地势高于东北部分,实验地海拔最高为96.2 m（荧光剂投放点）和下游测点海拔最低为88.8 m。

2 实验方法

2.1 投放荧光剂和测量背景浓度

在里韦林河道上游选择有利于溶质在河流横截面方向快速混合的地点作为投放点,为避免对河流水质造成污染,本实验采用荧光剂示踪剂作为污染物的替代品,荧光剂的优点是每一个分子有独特的激发和发射波长,不需要进行生化反应实验可现场获取读数。本实验采用的荧光剂探测仪的灵敏度为0.02 ppb,由于仪器误差,在荧光剂从投放点运动到各测点之前,或没有投放荧光剂时,仪器仍会显示一些或正或负的背景读数,同时因为荧光剂经过较长距离的对流扩散等运动,在下游河水中的浓度较低,仪器读数较低,不易与背景浓度分辨。因此在投放荧光剂之前,需要在投放点和下游各测点取样,以便作为空白样本,消除仪器误差和背景浓度对实验的影响。

2.2 测量下游荧光剂浓度

下游各测量点之间应有适当的间距,以利于了解河流中污染物浓度时间分布随距离的变化。本实验中从上游到下游依次排列为测量点10、测量点6、测量点7、测量点8,测量荧光剂的浓度与时间数据集,并在每个测量站点绘制浓度与时间图,

本次实验在同一投放点共投放三次荧光剂,实验人员需要分别在投放点下游的4 个不同的测量点,在相同的时刻和时间间隔测量河水中的荧光剂浓度,然后绘制四个不同测量点的浓度随时间变化,见图1。

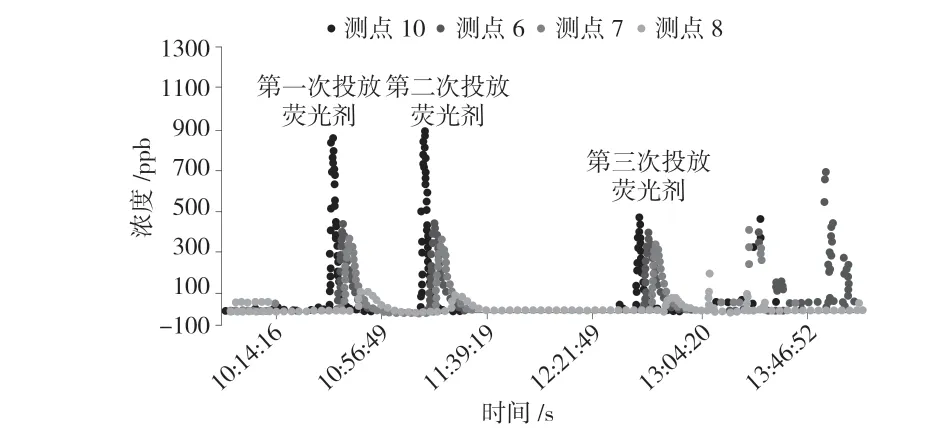
图1 不同测量点荧光剂浓度随时间变化图

2.3 其他相关数据

实验人员从河流左岸到右岸依次等距（0.5 m）测量从河底到河面的深度,目的是计算河道断面总面积,需要测量投放点与各测量点之间的直线距离、曲线距离和高度差,以求得计算河床坡度,另外还需要各测点的水流平均流速。

3 建立对流扩散模型

3.1 数据处理

在实际现场实验中,共投放三次荧光剂,然而第三次投放形成的测点10 浓度时间曲线的峰值比前两次要低,这意味着它在重复实验中与前两次实验表现不同,此外测点10 的位置接近投放点,因此舍弃测点10 的数据。出于实用性和篇幅的考虑,本文仅以测站6 和测站8 的数据为例,通过第一次荧光剂投放后的浓度时间分布来研究对流和扩散过程,见图2。

图2 第一次投放后测点 6 和测点 8 荧光剂浓度与时间关系图

数据处理需要去除各测点的背景噪音。分别从测点6 和测点8 在荧光剂到达之前的平坦区域选择5 分钟时间段,并计算这段时间内的平均浓度,将其作为此测点的荧光剂背景读数。从所有的浓度数据中减去背景读数并将负读数设置为0。图3 显示了去除背景读数前后的0～10 ppb 浓度区间的放大图。

图3 背景读数部分放大图

在一次投放形成的荧光剂羽流全部离开一个测点后,下一次投放形成的荧光剂羽流会逐渐运动到该测点。因此需要识别该测点上一个羽流与下一个羽流的连接点,即读数停止减少并开始增加的时刻,数据处理的方式是将所有低于临界值（由峰值浓度的1%、3%和5%定义）的数据集剪裁,并且识别点之前和之后的浓度应设置为0。图4 给出了以峰值浓度的5%为裁剪点处理后的测点6 和测点8 的浓度时间图。

图4 测点6 和测点8 的5%临界点

3.2 建立对流扩散模型

在已知上游浓度随时间变化的情况下,本对流扩散预测模型将有助于了解其运动到下游测点的浓度时间分布。通过计算分散系数,根据一对上下游测站的荧光剂浓度时间剖面,可以建立对流扩散模型。

河流中溶质的混合过程由对流、扩散、局部水流紊动组成。在忽略局部水流紊动的情况下,将前两个物理过程用下面的对流扩散方程方程来表示。

式中：x、y、z 为坐标尺寸,x 为纵向,y 为横向,Z 为垂向；u、v、w 为x、y、z 方向的速度分量；e 为扩散系数；c 为浓度。

由于仅研究基于河流流动方向的纵向混合,下游测点的荧光剂浓度的一维解被简化为如下对流扩散方程：

式中：C（xds,t）为下游测量点xds时间t 时的浓度；C（xus,γ）为上游测量点xus某时刻的浓度；T 为微小时间段内的荧光剂从上游运动到下游测点的时间；Kx为纵向分散系数；t 为预估下游浓度的时刻与上游投放时刻之间的时间间隔；dγ为每个微小时间段的持续时间。

由上游荧光剂浓度Cxus推算下游荧光剂浓度Cxds需要利用微积分的思想,关于上游测点的浓度分布可以看作是很多次荧光剂投放,每一次投放一个微小时间段γ内的荧光剂总量,Cxus以测点6 和测点8 为一对上下游组合,测点6 的荧光剂经过一段行进时间后运动到测点8,测点6 的浓度分布可以拆分成多次的微小投放,每一次微小投放在下游测点8 都会形成相应的浓度Cxds。叠加同时刻各下游测点8的微小浓度值,构成下游荧光剂浓度实际分布,见图5。

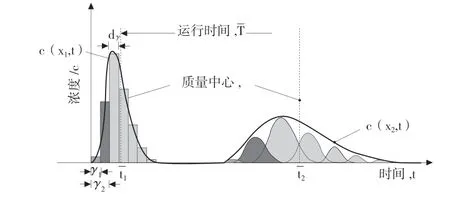
图5 对流扩散模型叠加原理示意图

3.3 检验质量平衡

上游及其相关下游测量点之间的溶质质量平衡是对流扩散模型的基础。上下游测点的羽流内溶质质量是分别是其浓度与时间曲线下方的面积,可以通过计算下面的方程来解决。

然而,由于测量误差和截面混合不完全,上下游的真实数据始终不能进行质量平衡。因此,通过将所有下游数据都乘以上游质量和下游质量之间的比率MB 来实现质量平衡。

通过计算得到测点6 和测点8 质量平衡结果。测点6：Mus=116313.6；测点8：Mds=52453.1；MB=2.2,见图6。

图6 质量平衡

3.4 确定模型参数

通过求解下面的力矩方程,可以得到方程2 中的临界系数Kx。

3.5 优化模型参数

本实验共投放3 次染料,有4 个荧光剂浓度测量点,可以将未用于组建对流扩散模型的上游测点的数据输入模型中,预测下游测点的浓度,判断预测值是否与经质量平衡处理后的实际值吻合。之后通过计算参数Rt2来检查对流扩散模型预测的优劣,使Rt2越接近1 的参数值最好。最后,对参数进行优化,使预测数据与真实数据最大程度地吻合,正式建立模型。

式中：mt为下游经质量平衡后的实际浓度；pt为下游预测浓度。

通过不断改变Kx、裁剪点和不同的测量点组合,得到在Kx=0.75 时,Rt2等于0.93 接近于1,最终以Kx=0.75 建立用于预测上游污染物排放对下游河流影响的对流扩散模型。

3.6 水质模型耦合

对流扩散模型可以与其他模型相结合,例如借助SOBEK模型与下水道模型结合[1],获得排污口溢漏特征,可以应用在河流中设置合流式排污口,排放经处理后达到排放标准的城市污水,预测下游不同距离的污染物浓度,以减轻城市污水处理的压力。又如与河道水文模型结合,有助于获得准确的河流流量,分析污染物扩散到下游的预测浓度剖面和危害程度,可用于航运过程中的船舶污染物泄露后的情况,及时做好应对措施。

3.7 预测不确定性

就对流扩散模型本身的准确性而言,还存在很多不确定性。一是混合过程还取决于局部水流紊动,而局部水流紊动随时间和位置的不同而变化很大。更具体地说,局部水流紊动在不同时间的表现并不相同,并且涉及很多物理量,包括粗糙度、泥沙输送速率等。然而,它们在每个河流断面都是可变的和多样的。

此外,对流扩散模型中有很多假设,例如质量平衡甚至流量等。但河床上存在涡流和污染转化,因此上下游质量不平衡。此外,流量假定为速度乘以横截面积。然而两者都是近似值,并且随时间和空间的变化而变化。

4 结语

对流扩散模型可以定量预测城市河流中污染物的输移和扩散过程,为保护生态环境和保证水资源安全提供支持,希望此模型可以在类似河流水质预测中起到一定借鉴作用。