数学好教师教学之新境

【摘  要】  为使数学优秀教师步入新境，把数学教育做得更好，提出十个“走向”供参考：从生答到生问、从学会到会学、从双基到三维、从三维到素养、从好玩到玩好、从教会到教慧、从智力到非智、从题海到题根、从无疑到生疑、从小气到大气.

【关键词】  数学好教师；教学;新境

有好的教师，才有好的教育.谁赢得教师，谁就赢得未来.

数学优秀教师，教精其术，教明其道，教取其势，教有其思，教专其业，托起了一方教育的璀璨星空.

从优秀走向卓越，还要什么？我以为，还要步入新境.

就教学而言，教师把学生“教会”了，是一种境界，如果教师把学生“教慧”了，教师的教学就步入了一个新的境界.教学，从生答到生问、从学会到会学、从无疑到生疑、从小气到大气……教师可以做的更好.

1  从生答到生问我们的学生不善“问”，是不争的事实.

美国学者布鲁巴克曾说过：“最精湛的教学艺术，遵循的最高准则就是让学生能够自己提问题.”提出问题是思维的动力，是创造的基石，也是解决问题的重要途径.爱因斯坦也认为“提出一个问题比解决一个问题更重要”，所以教师在教学中应注意培养学生“问”的能力.教师要激起学生爱问的冲动，善待每个学生的提问，使不同水平的学生都得到锻炼.

教师对有价值的提问，“点赞”之后要引导学生认真探究；对于价值不大的提问，要区别对待，采取妥善的方法予以处理，以保护、鼓励学生提问的积极性.对于后进生的提问要“高看一眼”，多用激励性语言赞赏之.

值得一提的是，有观点认为：“让学生提问难，教师转变更难，最大的阻力来自教师自身.”当学生所提的问题“井喷”时，老师招架得住吗？当整堂课被学生杂乱无章的“问题泡沫”包围时，老师还能收放有度地驾驭好课堂吗？当教师习惯于“自问自答”的教学方式受到挑战时，老师能克服固有的教学定势吗？

从“生答”到“生问”，教师准备好了吗？2  从学会到会学

“学会”，只是说在学习过程中掌握了某种知识和技能；“会学”，则是指在学习的过程中掌握了学习方法，形成了学习能力.

一个学生要想取得优良的学习效果，单靠教师教得好、教得得法是不行的，他自身还必须学得好、学得得法.遗憾的是，长期以来，在教育理论和教育实践中，教学多研究教，少研究学.实践证明，忽视了学，教也失去了针对性，减弱了其实效性.

教师“教学”，不仅包含教师的“教”，还应包含教师教学生“学”.

课例1  （爬楼梯问题）有人要上楼，此人每步能向上走1阶或2阶，如果楼梯有10阶，他上楼共有多少种不同的走法？我们用an表示上n阶楼梯的走法种数.

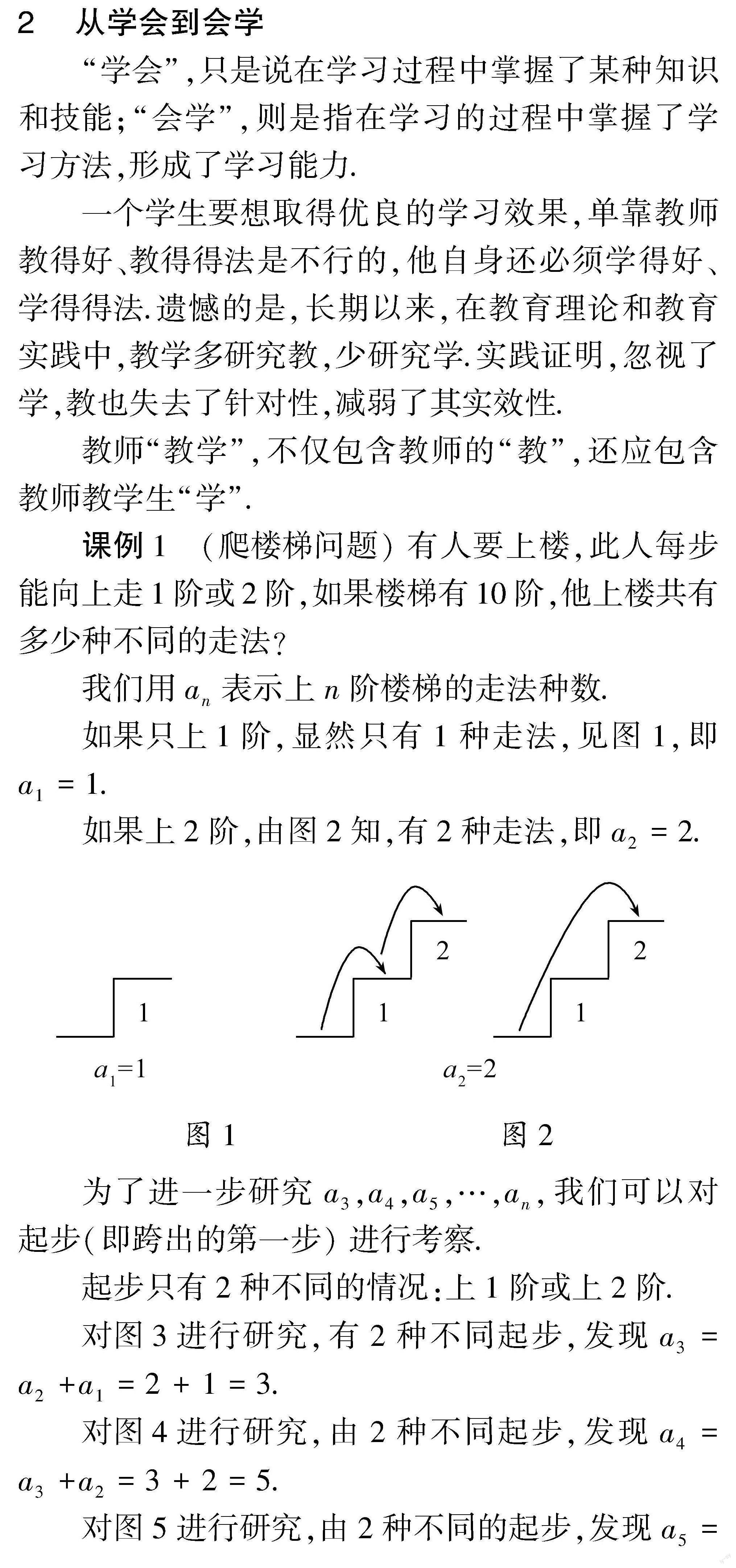
如果只上1阶，显然只有1种走法，见图1，即a1=1.

如果上2阶，由图2知，有2种走法，即a2=2.

为了进一步研究a3，a4，a5，…，an，我们可以对起步（即跨出的第一步）进行考察.

起步只有2种不同的情况：上1阶或上2阶.

对图3进行研究，有2种不同起步，发现a3=a2+a1=2+1=3.

对图4进行研究，由2种不同起步，发现a4=a3+a2=3+2=5.

对图5进行研究，由2种不同的起步，发现a5=a4+a3=5+3=8.

离开图形，我们可以用同样的方法将起步分为两类——上1阶与上2阶，又可以得到：

a6=a5+a4=8+5=13，a7=a6+a5=13+8=21，…，进一步得到

an=an－1+an－2（n≥3）.

由此，我们可以依次计算，得出下表：

从表中我们知道，上10阶楼梯，共有89种不同的走法.

如果楼梯有20阶、30阶，又该怎么算呢？显然可以继续列表算出，但计算量不断加大，这时你一定会产生一个数学企望：去研究出一个计算它的公式该多好！

对“起步进行考察”——可分为两类，这就是很好的思维方法，逐步引领学生步入“会学”之境，进而领悟斐波那契数列问题的真谛.3  从双基到三维传统的教学方式，是“带着知识走向学生”，强调“双基”教学，即基础知识和基本技能教学.新课程改革的一个重要标志，就是要求教学从“双基”走向“三维”.

“三维”是指“三维目标”，它是指教育教学过程中应该达到的三个目标维度，即知识与技能，过程与方法，情感态度与价值观.“三维目标”是一个教学目标的三个方面，而不是三个独立的教学目标，它们是统一的不可分割的整体.

我们强调“三维”并不否定“双基”.我国学生具有良好的“双基”，这是几代教育工作者努力的结果.“双基”教学应在继承倡导中反思，在反思中进一步发展.“双基”是一个随时代发展、随教育实践不断深化而有不同内涵的概念.

优秀教师，应是积极践行发展“双基”观的教师，更应是智慧达成“三维”目标的教师.

課例2  （电动扶梯上下跑）到商场购物，电动扶梯有上行的也有下行的.我看见个别不太听话的小孩，在电动扶梯上下跑动，这是很不安全的.尤其是当电梯上行时小孩往下跑，或当电梯下行时小孩往上跑，“逆向跑动”危险更大.

不过从数学角度来研究一番，倒是一个有趣的话题.

我们要研究的问题是：电梯上行时一个小孩跑一个来回与电梯下行时这个小孩跑一个来回，那一种“跑法”更快？还是各有“抵消”，是否“一样快”？

我们设小孩上行、下行的速度分别为v1、v2，小孩下行速度比上行速度快，即v1<v2，电动扶梯上行和下行速度相同，设为v，电动扶梯的长度为s.

显然，应有v<v1<v2.否则，若v≥v1，则电动扶梯下行时，小孩永远“跑不上去”；若v≥v2，则电动扶梯上行时，小孩永远“跑不回来”.

电动扶梯上行时，小孩跑一个来回所用的时间为

sv1+v+sv2－v；

电动扶梯下行时，小孩跑一个来回所用的时间为

sv1－v+sv2+v.

因为v<v1<v2，所以

sv1+v+sv2－v－sv1－v+sv2+v

=s1v1+v－1v1－v+1v2－v－1v2+v

=s－2vv21－v2+2vv22－v2

=2sv（v21－v22）（v21－v2）（v22－v2）<0.

哇！前者跑得快！即电梯上行时一个小孩跑一个来回，要比电梯下行时这个小孩跑一个来回快.

这样的问题，其运算没有“双基”不行，其“解决问题”是走向“三维”的过程.

4  从三维到素养

时代在发展，世界在变化.“如何培养学生的核心素养”，已成为世界主要国家的关注话题，我国也发布了中国学生发展核心素养总体框架和基本内涵.专家指出，落实“双基”是课程目标1.0版，落实三维目标是2.0版，落实核心素养是3.0版，核心素养的提出让教育改革进入“3.0时代”.如果说从“双基”走向三维目标是新一轮课程改革的一个标志，那么从三维目标走向核心素养，则是当前课程改革全面深化的一个标志.值得厘清的是，核心素养之于三维目标并不是简单的取代，更不是否定，而是继承中发展，传承中创新，整合中突破.从形成机制来讲，核心素养是三维目标的进一步提炼与整合，是通过系统的学科学习之后而获得的.三维目标是核心素养形成的要素和路径.

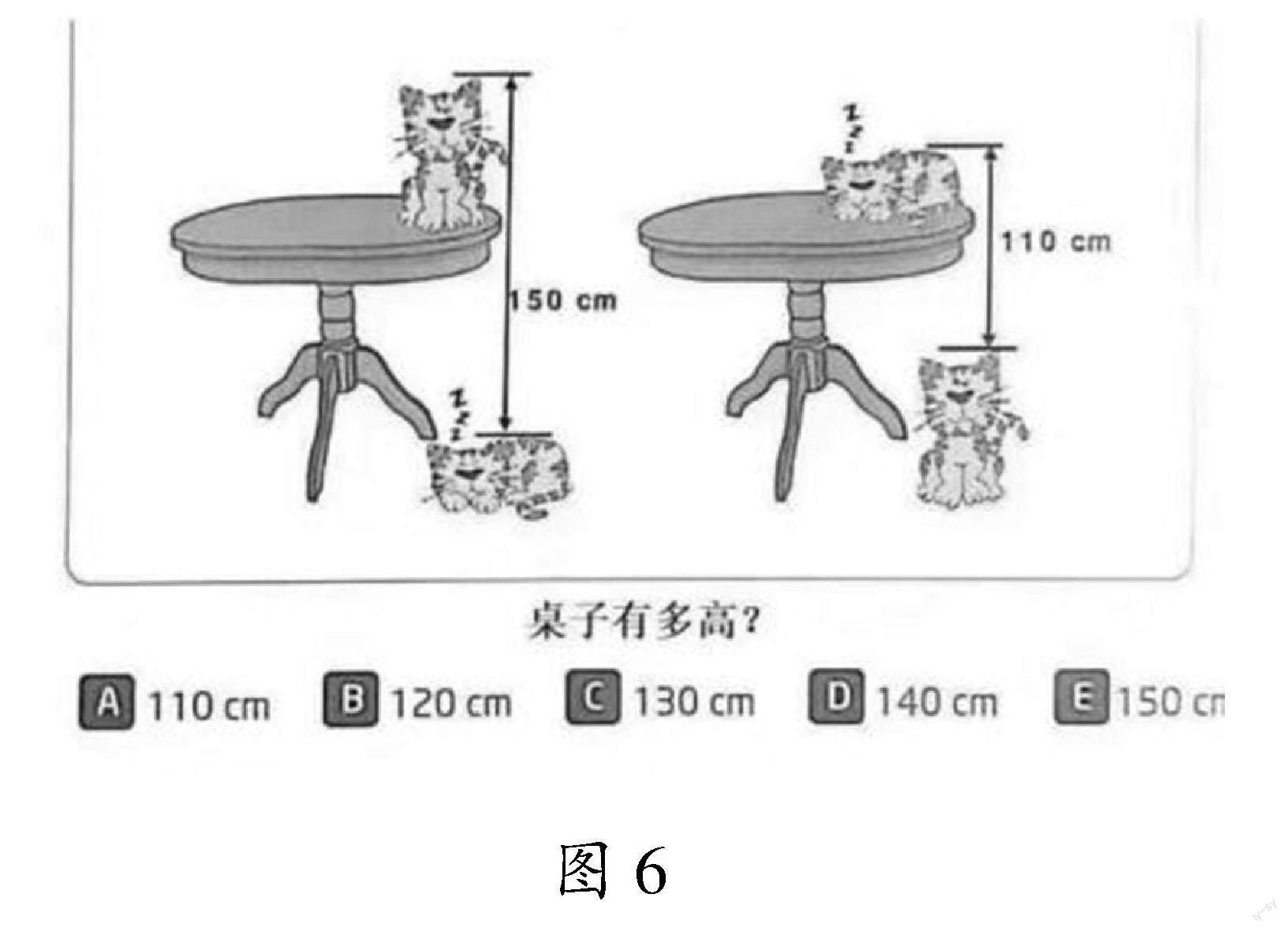
课例3  （桌子的高度）曾经有学生家长发给我这样一道四年级的题：给出下面两幅图，求桌子的高度.

我觉得这道题是非常好的“素养题”，数学观察、数学直觉、广义对称、消元思想等，都在“瞬间”考察到了.

我在家长群里这样说：“不要拿笔，30秒正确解答者，优秀；60秒正确解答者，良好；90秒正确解答者，及格.”家长群“爆棚”——出现流眼泪、苦瓜脸、尴尬相、捂脸等表情图——直言：“我们都不及格.”读者朋友，不妨也试试，考一考你的数学素养！

5  从好玩到玩好

“好玩”就是“引趣”，让学生感到学习十分有趣，这是学习的原动力；“玩好”就是“引深”，让学生能不断钻研深入探索，这是学习的内驱力.当数学教师很不容易，“数学好玩”要求我们“深入浅出”，而“玩好数学”要求我们“浅入深出”.从“数学好玩”到“玩好数学”，需要数学教师坚持研修，把握好数学的横向联系和纵向深入，把握好数学的趣味性和拓展性，结合学生实际，将数学的“好玩”和“玩好”像知时节的“好雨”适时润入学生的心田.

“好玩”是要让所有学生都能感受到的，“玩好”就不能要求所有学生一定都達到，这里有一个“度”的把握.“好玩”是一种境界，“玩好”是略高一层的境界，而在“好玩”与“玩好”之间把握好“度”就是一种理想的状态，需要灵活运用“引趣”和“引深”.

课例4  （由上转下）把6枚小圆片，摆成如下的正三角形.

请你移动2枚圆片，摆成一个倒正三角形.好玩吧？幼儿园大班的孩子就可以玩.

玩完了，我观察学生干什么.若学生什么也没做，这学生此时算是浅层次的“好玩”；若学生会拿起桌上的小圆片摆成4行、5行，研究要移动几枚才能摆成一个倒正三角形，那就算是高一级的“好玩”；若是初中生，就要研究更多行的情况，步入“玩好”；若是高中生，就要研究一般情形，真正地“玩好”.

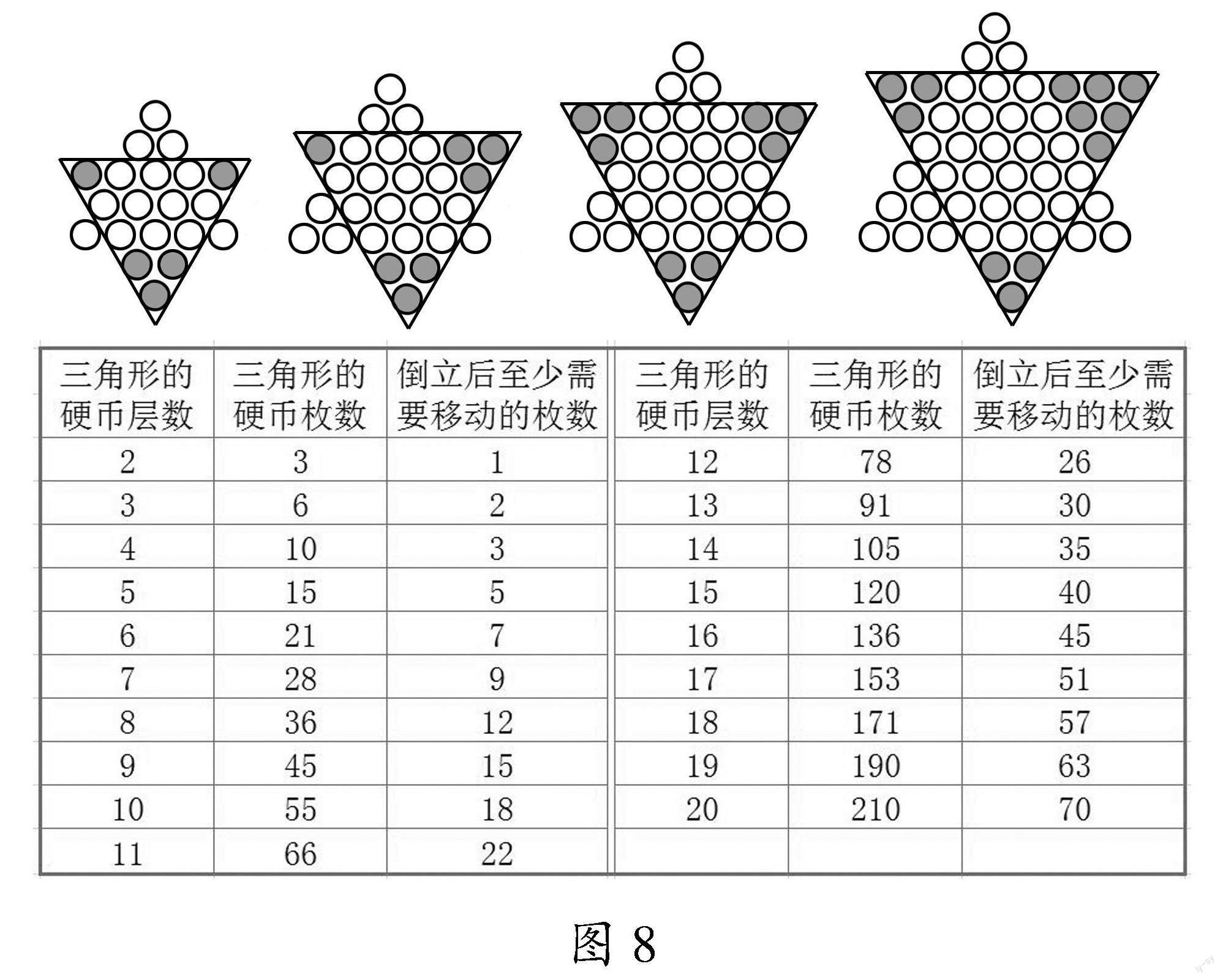
数学教师要引导学生学会探索一般性问题.就本题而言，就是探索“n 层小圆片的移动问题”.探索之路：4层最少要移动3枚小圆片；5层最少要移动5枚小圆片；6层最少要移动7枚小圆片.当层数增加时，我们可以利用一个倒三角形来研究这个问题，并得出一般结论.

一般结论为：n为正整数，从3n-1层起到3n+1层止，每增加一层，需要移动n枚圆片.让这题成为某年的高考题，指向“解决问题”，不超纲吧？6枚小圆片，我们玩出了一片“新天地”.

6  从教会到教慧

教师教学生学会课本上的知识、记忆这些知识，力争考出一个好的成绩，也就是我们常说的“教会学生”.这无疑是需要的，也是教师教学的最基本要求.

一个教师热爱本职工作，对学生负责，忠于职守，认真备课、上课、批改作业、辅导学生.实事求是地说，要做好这一些，也非易事.张奠宙、赵小平教授曾写一篇《做一个与时俱进的教书匠也不容易》的文章，这里所说的“与时俱进”指的是“教师最好能更多地研究教育规律，更积极投入教育改革的潮流.”

“与时俱进”在我看来还可以再“俱进”一点，那就是从“教会学生”走向“教慧学生”.就“知识”教“知识”培养出来的学生，难以更好地适应未来，只有让学生获取知识的学习过程充满素养培育、充满智慧灵动，才能更好地迎接未来的挑战.

课例5  （搭“桥”）给出15块多米诺骨牌和图9，请用这15块多米诺骨牌搭成图9的“桥”.只能自己一个人玩，不能“同伴互助”.我激学生：“30秒够吗？”

学生搭这个“桥”，绝大多数是想靠“心灵手巧”搭成，一般不能成功；一些学生试图先“躺”着摆，然后立起来，单人操作也难成功.5分钟过去了，还是没人摆出来.

什么叫智慧？我们给学生讲心理学的界定，他们很难理解.我们和学生玩游戏——比如这个搭“桥”游戏，就能让学生深刻领悟什么叫“智慧”.图10

我对学生说，这样搭“桥”，手很巧但没用脑.用2根撑起13根，重心不稳难成功.怎么办？能否“借力”——一开始多放两块做“桥墩”，当搭好更多的骨牌后，“桥”的构架也就稳定了，这时可以把多余的“桥墩”取走，完成“搭桥”任务.

整个搭“桥”的过程，充满智慧.

7  从智力到非智

智力因素一般指注意、观察、记忆、想象、思维，非智力因素（狭义）一般指动机、兴趣、意志、情感、性格.在教学中，智力因素是十分重要的，它在学生分析问题、解决问题中起着核心作用，而思维能力又是核心的核心.因此，教学中应不失时机地全方位地对学生进行智力训练，培养学生高度的注意力、敏锐的观察力、高超的记忆力、丰富的想象力和广阔的思维力.

但教学中又应强调非智力因素的辅助作用，培养学生具有远大的理想、浓厚的兴趣、顽强的意志、丰富的情感和刚毅的性格.只有智力因素与非智力因素有机结合，才能使学生以极大的热情参加学习活动，并能使学生在学习活动中充分发挥水平取得好成绩.

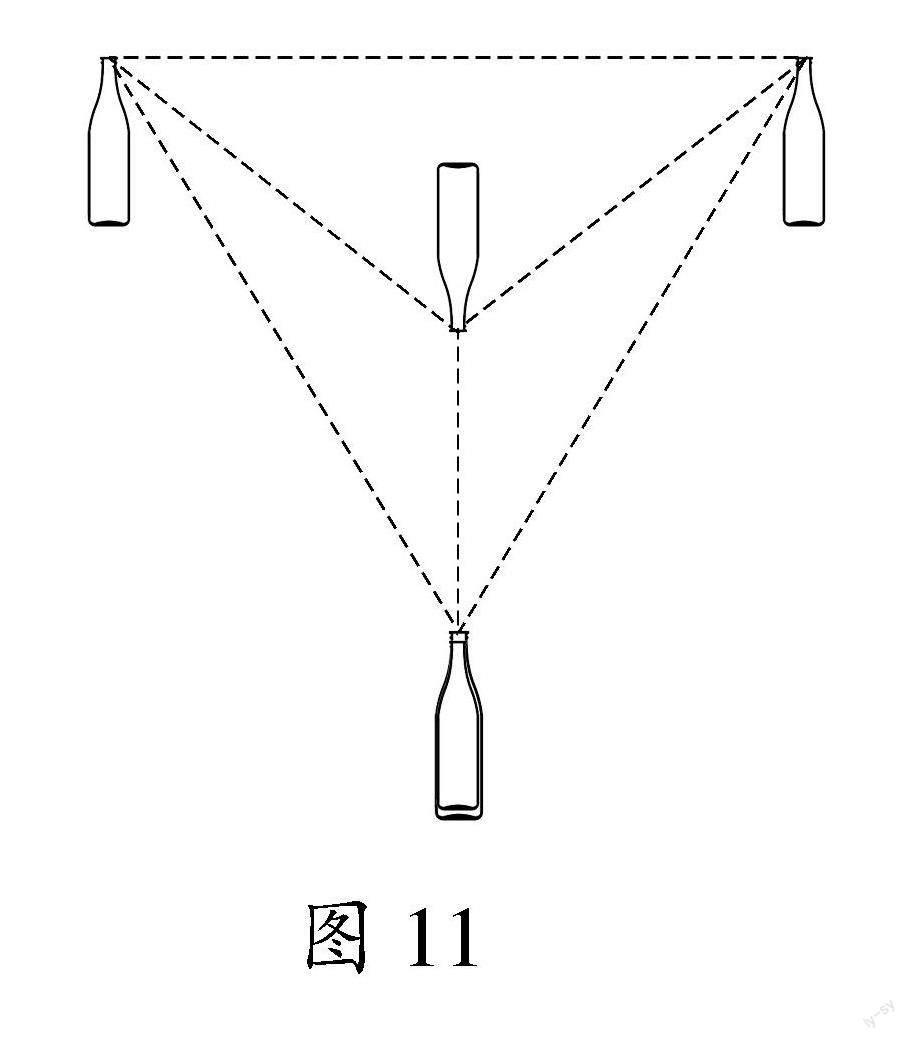
课例6  （四个瓶子）什么是立体几何？我们可以从“4个瓶子”玩起：给出4个同样大小的啤酒瓶.你能摆放得使任意两个瓶口中心之间的距离都相等吗？图11

许多学生摆了几次都没成功.让我们展开想象的翅膀，突破思维定势，把其中一个倒过来放，啊哈，成功了！

摆法的背后，就是“立体思维”，就有空间想象，就有立体几何的意味.立体几何，从某种角度说，也可以说成是“不同面上的平面几何”.这道小题，没有更多的数学知识.从智力角度来说，更多的是想象力；从非智力角度来说，就是激发兴趣、引发情感.

8  从题海到题根

时至今日，中小学生课业负担过重的问题并没有得到彻底解决，仍是困扰基础教育发展的一个顽疾.要“优化作业和练习”，就不能再依靠“题海战术”.“题海无边，何处是岸？”从某种角度说，我以为“题海无边，题根是岸.”

课例7  （糖水不等式）已知：a，b，m∈R+，且a<b，求证：a+mb+m>ab.（1）一题多解的教学价值.

第一节课，师生共同探讨了分析法、综合法、求差比较法、求商比较法、反证法进行证明，课堂练习之后，再探讨放缩法、构造函数法、增量法进行证明.这节课的作业是“研究本题的第九种新证法”，学生可独立思考也可集体攻关.

第二节课，让有新证法的学生讲新证法，师生又共同探讨了定比分点法、斜率法、三角法、几何模型法新证法，课堂练习之后，继续探究，师生又得到用正弦定理法、相似三角形法、换元法、双换元法、综合法及放缩法、定义域及值域法的新证法，让学生感受到“柳暗花明又一村”.这节课的作业是“研究本题的第二十种新证法”，学生可独立思考也可集体攻关.

第三节课，老师问学生有谁还能再开动脑筋、挖掘潜能、探寻新证法，继续引导学生探索用椭圆离心率法、双曲线离心率法、函数图象法、两直线位置关系法、矩形面积法、定积分法进行证明.学生步步惊愕，全班沸腾了！这节课的作业是“在未来的日子里，研究本题的第二十六种新证法”，学生可独立思考也可集体攻关.

这道题让学生“透视”一个简单不等式问题背后的博大精深的“世界”，学生在探索新证法的过程中进一步体会到数学知识之间的联系，启迪学生更深刻地“悟道”数学解题的奥妙与真谛.

（2）一题多变的教学价值.师生共同探索“变式”，层层深入，共变出8个新的命题，最后一个是：

若ai，bi∈R+，i=1，2，…，n.

且a1b1<a2b2<…<anbn，则

a1b1<a1+a2b1+b2<…<a1+a2+…+anb1+b2+…+bn<a2+a3+…+anb2+b3+…+bn<…<an－1+anbn－1+bn<anbn.

“真过瘾！”这是学生们用换元法或增量法证得“猜想”成立时发出的感叹.

（3）一题多用的教学价值.利用本題的结论，“借题发挥”，可解决多个数学问题，其中包括某年高考最后一题所要证的不等式：

（1+1）1+131+15…1+12n－1>2n+1（n∈N，n≥2）.当学生得知，他们无意中解决了高考“压轴题”时，先是惊得目瞪口呆，继而发出会心的微笑.他们感觉到了自身的力量，进一步增强了学好数学的信心.

9  从无疑到生疑

绝大多数教师为了圆满地完成教学任务，都会力争把课讲得完整、细致、清晰，也就是讲得很完美、很“干净”，讲得“没有疑问”.一位英国外教在接受媒体采访时说，中国学生最大的问题是“没有问题”.

中国教师要清醒地认识到，学生没有提出问题，不等于就没有问题！

中国学生为什么“没有问题”？原因之一是中国的老师们“不会生疑”.

课例8  （谁先到达）一辆汽车P从A沿半圆弧运动到B，另一辆汽车Q从A沿两个等半径半圆弧运动到B，见图12，两汽车运动速度相同，问哪辆汽车先到点B？

这是一道小学生都会解答的智力题，容易通过计算得出P、Q同时到达点B.绝大多数学生做完此题也就完事了，不善于通过推广与变式把问题深化，失去了一次极好的训练创造性思维的机会.

我引导学生不断深化.

深化1：把“两个半圆”改为“n个半径相等的半圆”，情况如何？见图13.

小学生也可以证明，同时到达.

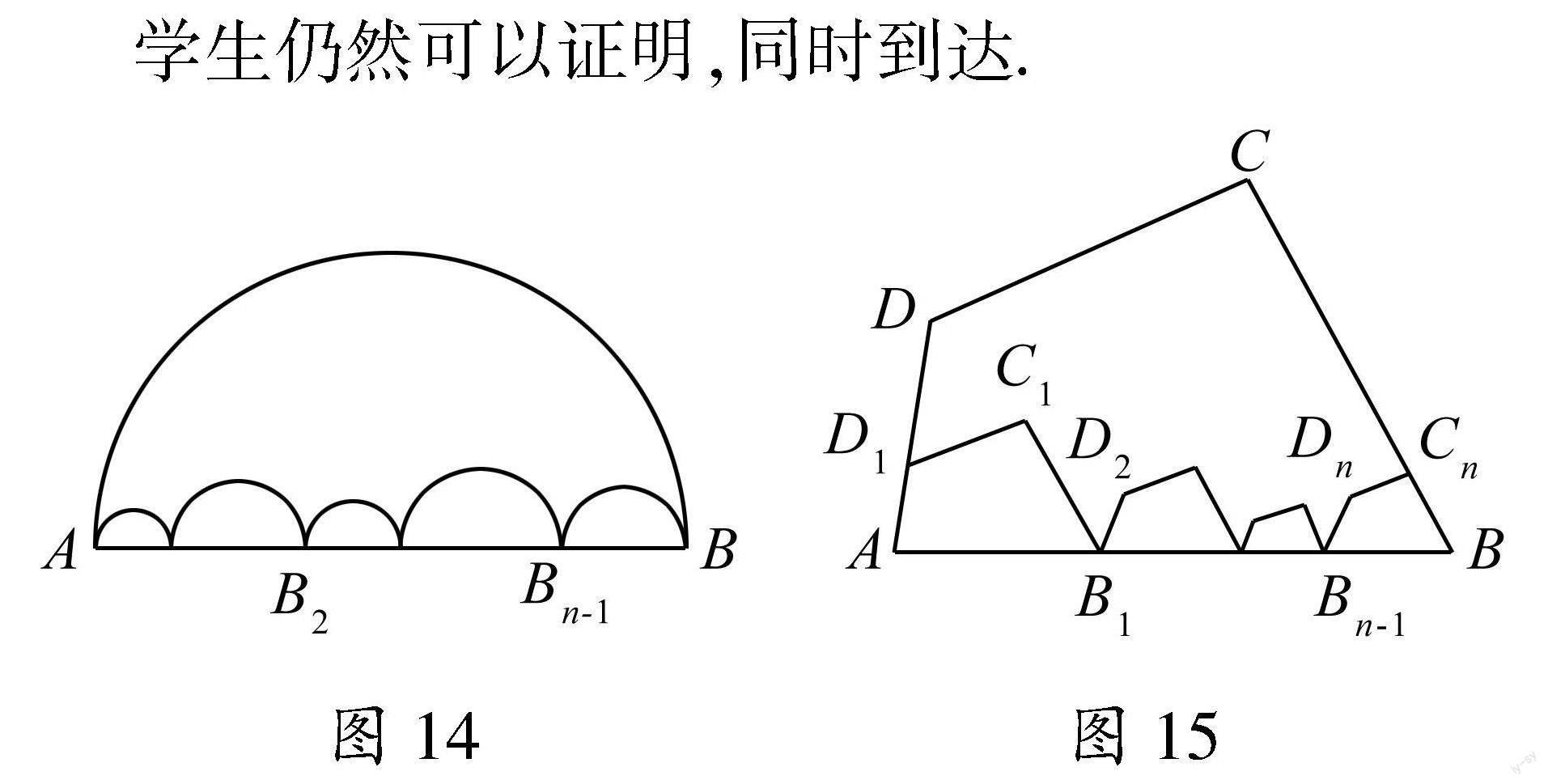
深化2：“线段AB上有n个半圆（半径允许不相等）”，情况如何？见图14.

学生仍然可以证明，同时到达.

深化3：如图15，图中凸多边形均相似，是否有

AD+DC+CB=AD1+D1C1+C1B1+B1D2+…+Bn-1Dn+DnCn+CnB？

初中生可以用相似多边形性质，证明结论正确.

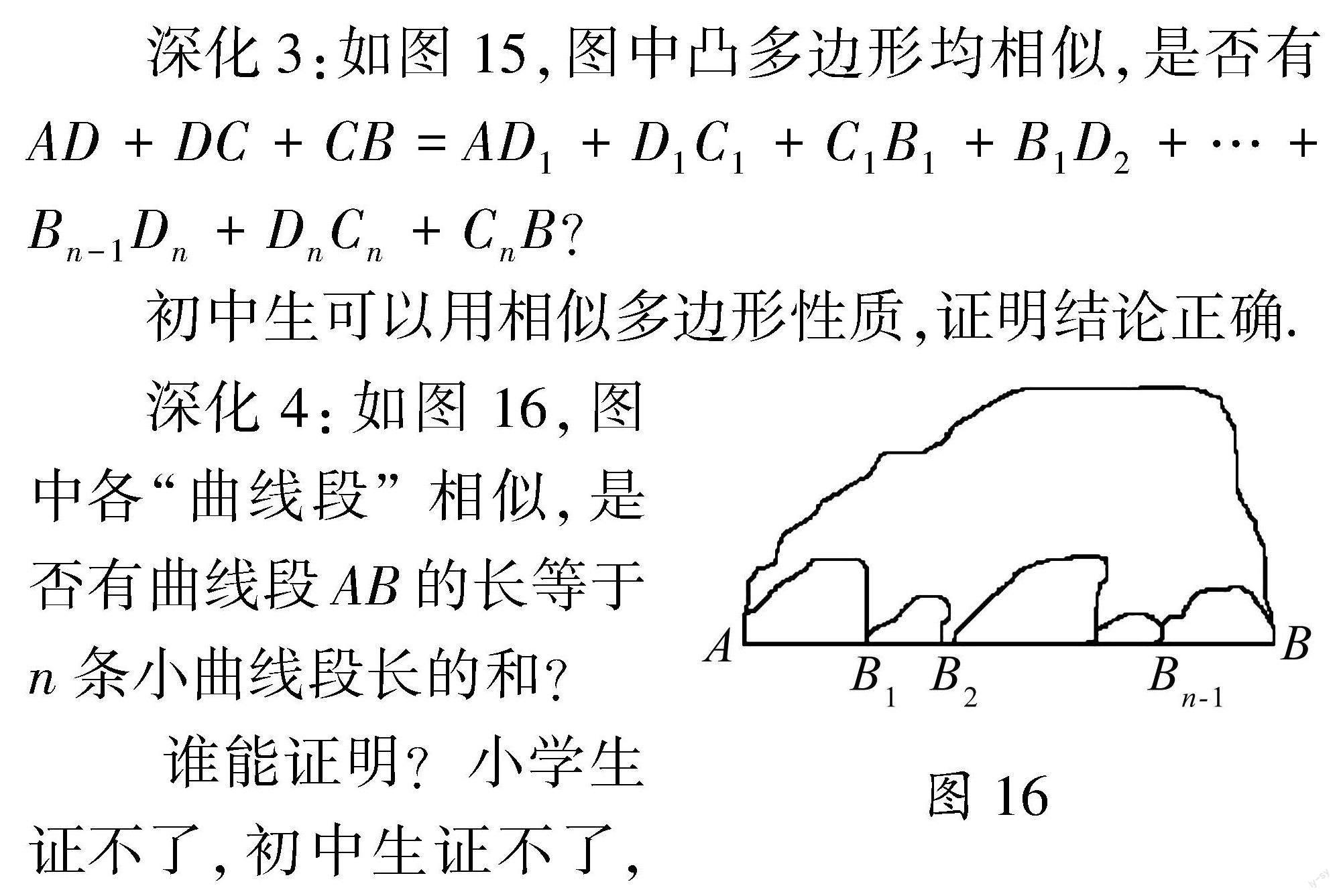
深化4：如图16，图中各“曲线段”相似，是否有曲线段AB的长等于n条小曲线段长的和？

谁能证明？小学生证不了，初中生证不了，高中生也证不了，只有大学生才会证.不过这个大学生要学了定积分之后，才能证明结论正确.具体的证明方法，就留给读者去探索吧！好好的一道题，怎么“整出”那么多问题？

10  从小气到大气

当下中小学课堂教学，总的说来“大气不足”.这固然与现行的教育评价和考试制度有关，但也和教师的教学观念、知识积累、能力水平、文化素养等有关.即便是为了测评和升学，我们的课堂教学也完全可以大气一些.

“小气”的表现是多方面的.以数学教学为例，数学概念教学的“掐头去尾烧（鱼）中段”的干焦面孔，而忽略了对数学知识的火热的思考；钻数学解题教学的“特技特法”，而忽略了数学解题教学的“通性通法”；以高考中考不考為由，扼杀学生对数学知识和数学问题适当延伸的渴望；不重视“选学内容”，甚至视“选学内容”为“不学内容”;等等.

课例9  （最美等式）某数学教师上“复数”最后一课，书上有“小体字”的选读内容，讲复数的指数形式等.我听课时，以为老师会有“最美等式”的生动故事，没想到老师却说：“大家功课紧，选读内容就不读了吧，可预习‘小体字’之后的解析几何内容.”我当时的反应是：“老师啊，你不能这么‘小气’，没文化啊！”

“eiπ+1=0”是传播“数学文化”的很好案例，也是激发学生喜爱数学的极好案例，如此“失之交臂”实在可惜！

我每次教复数时，都会这样讲：……奇巧而有趣的是，数学中的“五朵金花”——中性数0、基数1、虚数单位i、圆周率π、自然对数的底数e，竟能开在同一棵树上，组成一个“最美的艺术插花”—— eiπ+1=0，不可谓不绝！

我还让学生欣赏我为此写的数学小品文《数苑中的“五朵金花”》，学生在“意料之外”与“令人震惊”中，又一次体验到了数学之美、数学之奇、数学之趣.

我期盼数学教学大气一些，数学的横向联系与纵向深入，都需要我们大气.愿数学教师，能气度不凡、不落俗套，自觉成为有“文化”的数学教师，自觉成为“数学文化”的传播者，自觉成为有“文化”的教育者.

参考文献

［1］  任勇.觉者为师：好教师成长之新境［M］.上海：华东师范大学出版社，2019.6.

［2］  任勇.期盼数学教学“气”象万千［J］.数学通报，2011，50（09）：4550.

作者简介  任勇（1958—），男，河南信阳人，中学高级教师，数学特级教师；荣获“苏步青数学教育奖”一等奖，享受国务院政府津贴；主要从事教育管理、教师教育和数学教学研究.