因式分解中的数学思想

邹兴平

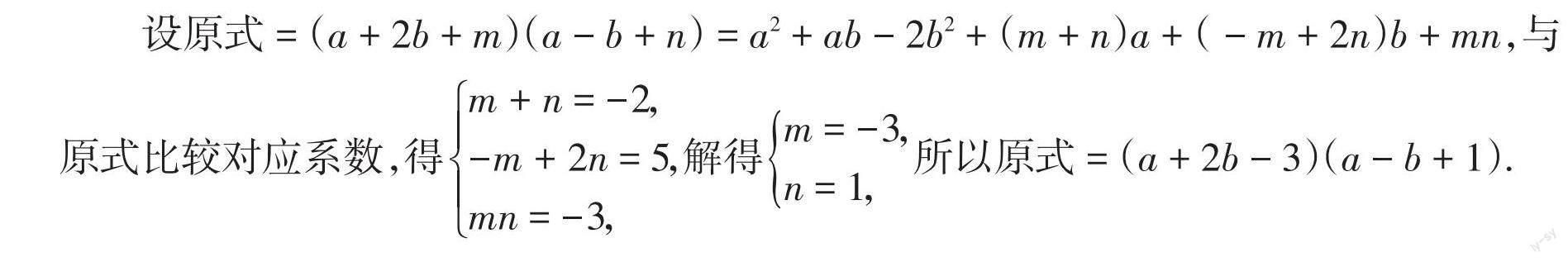
一、整体思想

整体思想就是将待求问题中的某个代数式视为一个整体，合理地转化其条件及结论的形式、结构，将问题转化到熟悉的知识范围内来解决的数学思想.

例1 分解因式x2 + 2xy + y2 - x - y - 2.

解析：从整体的角度出发，视x + y为整体，寻求解题的途径.

原式 = （x + y）2 - （x + y） - 2 = （x + y - 2）（x + y + 1）.

二、换元思想

换元思想是把某个代数式当作一个新的变元来实行变量替换的一种数学思想.换元法实质是整体求解法，只是将某一整体用另一个字母来代换.

例2 分解因式（xy - 1）2 + （x + y - 2）（x + y - 2xy）.

解析：显然，去括号后再分解不可取，但可以设x，y的和与积为辅助元来求解.

设x + y = a，xy = b，

则原式 = （b - 1） 2 + （a - 2）（a - 2b） = （a2 - 2ab + b2） - （2a - 2b） + 1

= （a - b）2 - 2（a - b） + 1 = （a - b - 1）2 = （x + y - xy - 1）2 = （x - 1）2（y - 1）2.

三、转化思想

转化思想是指把待解决或未解决的问题，通过转化，归结到已经解决或比较容易解决的问题中去的一种思想方法.

例3 分解因式x3 + 6x2 - 27x.

解析：提取公因式x后剩下x2 + 6x - 27，不能直接分解因式，可想办法转化为平方差公式分解.

x3 + 6x2 - 27x = x（x2 + 6x - 27） = x（x2 + 6x + 9 - 9 - 27） = x［（x + 3）2 - 62］

= x（x + 3 + 6）（x + 3 - 6） = x（x + 9）（x - 3）.

四、方程思想

从问题的数学关系入手，运用数学语言将问题转化为数学模型，如方程，然后求解，使问题得以解决的一种数学思想.根据多项式的特点设未知数，根据系数相等列出方程或方程组，求出未知数的值，达到分解因式的目的，这是方程思想的应用.

例4 分解因式a2 + ab - 2b2 - 2a + 5b - 3.

解析：利用分解因式的基本方法较难分解这个二次六项式，通过观察发现前三项可分解为（a + 2b）（a - b），设原式 = （a + 2b + m）（a - b + n），展开后运用待定系数法即可求出m，n.

设原式 = （a + 2b + m）（a - b + n） = a2 + ab - 2b2 + （m + n）a + （ - m + 2n）b + mn，与原式比较对应系数，得[m+n=-2，-m+2n=5，mn=-3，]解得[m=-3，n=1，]所以原式 = （a + 2b - 3）（a - b + 1）.

分层作业

难度系数： ★★★★     解题时间：8分钟

1.当[x4-12x3+54x2-108x+81]的值为1时，x的值为（        ）. （答案见第33页）

A. 2 B. [7] C. 2或4 D. 2或-4

2.分解因式（x + 1）（x + 2）（x + 3）（x + 4） + 1. （答案見第33页）

难度系数： ★★★★★     解题时间：4分钟

3.（2022·青海·西宁）八年级课外兴趣小组活动时，老师提出了如下问题：

将2a - 3ab - 4 + 6b因式分解．

【观察】经过小组合作交流，小明得到了如下的解决方法：

解法一：原式 = （2a - 3ab） - （4 - 6b） = a（2 - 3b） - 2（2 - 3b） = （2 - 3b）（a - 2）.

解法二：原式 = （2a - 4） - （3ab - 6b） = 2（a - 2） - 3b（a - 2） = （a - 2）（2 - 3b）.

【感悟】当项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

【类比】（1）请用分组分解法将x2 - a2 + x + a因式分解；

【挑战】（2）请用分组分解法将ax + a2 - 2ab - bx + b2因式分解；

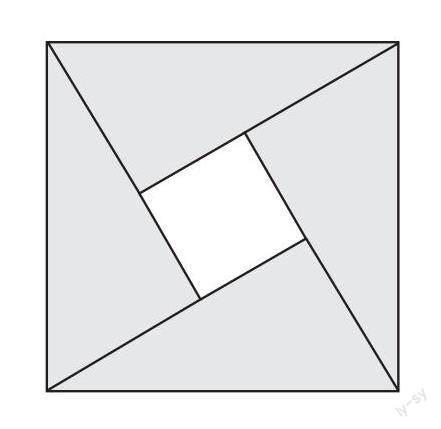
【应用】（3）“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理. 如右图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形. 若直角三角形的两条直角边长分别是a和b（a > b），斜边长是3，小正方形的面积是1．

根据以上信息，先将a4 - 2a3b + 2a2b2 - 2ab3 + b4因式分解，再求值．

（作者单位：湖北省恩施市龙凤镇民族初级中学）