基于多源数据融合与模糊聚类的电力工程数据处理方法研究
柯霖
(武汉中超电网建设监理有限公司,湖北武汉 430000)
电力工程针对电力系统的发输配变环节进行建设或改造,对保障系统安全、可靠运行具有重要意义[1-2]。随着用电服务需求的提升,电网公司对电力工程的精准投资及高效管理也越发重视。但目前其对于电力工程项目的风险管控主要以事后控制为主,这一管控方式不仅被动且效率较低,因此无法从根本上解决风险问题[3-5]。而电网公司在推进电力工程项目的过程中积累了海量数据,如何利用这类数据实现对工程项目的风险识别与智能管控,也是亟需解决的关键问题[6]。
针对上文所述,文中基于电力工程多源数据融合方法,通过将模糊C均值聚类(Fuzzy C-Means,FCM)、改进萤火虫算法(Improve Firefly Algorithm,IFA)与支持向量机(Support Vector Machine,SVM)相结合,实现了对电力工程项目风险的精准识别,并有效提升了相关项目监理管控的智能化水平。
1 电力工程风险识别指标体系
为了利用电力工程数据智能处理系统实现对多源数据的分析,对工程项目的风险进行精准识别并保障项目的质量,该文构建了如图1 所示的风险识别指标体系。该体系包括环境风险、技术风险、经济风险与管理风险四个方面的18 个关键技术指标。
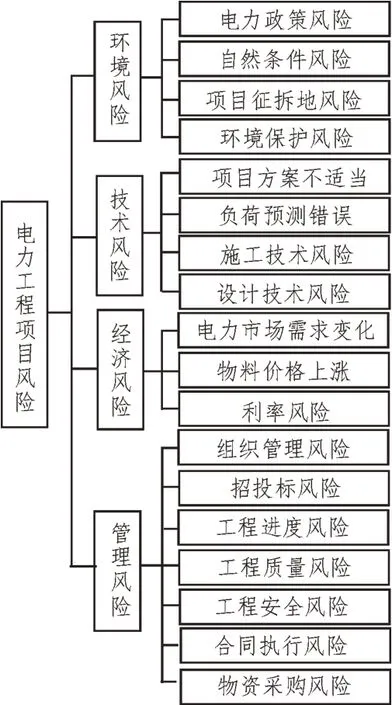
图1 风险识别指标体系框架
2 基于FCM-IFA-SVM 的工程项目风险识别方法
该文提出一种融合了FCM、IFA 及SVM 算法的电力工程项目风险识别方法,其结构如图2 所示。该方法首先采用FCM 对多源异构数据样本进行聚类分析,以减少不同簇类特征差异对后续风险识别过程的干扰;然后利用IFA 算法对SVM 模型的惩罚系数与核函数参数进行优化,从而提高SVM 模型的风险识别准确率;将聚类完成的数据输入优化完成的SVM 模型中,从而实现对电力工程项目风险的精准识别。
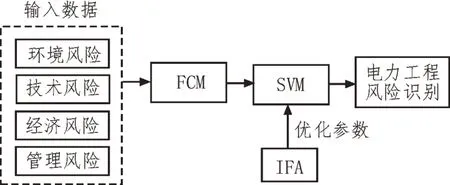
图2 FCM-IFA-SVM算法结构
由于FCM 具有计算过程简便、场景适应性较强以及收敛速度快等特点[7-9],故其在高纬度、大规模的多源数据融合分析中应用广泛。
假设输入数据集共有N个数据样本,每个数据样本维度为D维,则数据集可用矩阵的形式描述如下:
式中,X为输入数据矩阵。
FCM 算法经过聚类最终得到c个簇类,而各个簇类的中心为:
其中,zc为第c个簇类的中心,其定义为:
FCM 算法与其他聚类算法的不同之处在于,每个数据样本xn并非严格地划分至某一簇类,而是以模糊隶属度值的形式描述其归属于某一簇类的可能性。且数据样本之间的模糊隶属度满足以下关系:
式中,vnc为数据样本xn划分为簇类中心zc的可能性,即模糊隶属度;同时,每个数据样本归属于所有簇类的可能性之和为1。
因此,聚类迭代过程的目标即为令目标函数取值最小:
式中,β为权重参数;hnc为数据样本xn与簇类中心zc的笛卡尔距离,其计算方式如下:
其中,xnd和zcd分别为数据样本xn与簇类中心zc的d维特征值。
FCM 算法的基本过程为:从数据样本中随机选取初始化簇类中心;再根据模糊隶属度对其进行计算并更新;从而使式(5)中的目标函数达到最小。该算法流程如图3 所示。

图3 FCM算法流程
FCM 算法主要步骤如下:
1)参数初始化:输入FCM 算法簇类个数C及权重参数β,并计算代数上限G、精度阈值ε。
2)初始化模糊隶属度与簇类中心:随机选取C个数据样本作为簇类中心,且随机初始化模糊隶属度,进而令计算代数g=1。
3)根据模糊隶属度更新簇类中心:
4)根据簇类中心更新模糊隶属度,同时计算目标函数值:
目标函数值的计算方式如下:
5)判断是否满足终止条件,若是,则结束计算;否则,跳至步骤3)。终止条件为:
6)经过FCM 迭代计算后,得到最终的簇类中心及每个数据样本所属聚类中心的模糊隶属度值。再选取最大模糊隶属度所对应的簇类作为数据样本最终的归属:
式中,cn为数据样本xn所属的簇类,且其簇类中心为zc。
传统的FA 算法是模拟萤火虫利用光强度进行信息传递的行为机制[11-12],且萤火虫的光强度越大,对其他萤火虫的吸引力便越强。其中,萤火虫的吸引力计算方式为:
式中,φ0为初始吸引力;λ为光吸引参数;rij为位置在xi和xj萤火虫之间的距离,其计算方式如下:
式中,‖∙‖为二范数,d为待求解问题的解空间维数。
FA算法根据下式来计算并更新萤火虫所处位置:
在该次所采用的IFA 算法中,光强较弱的萤火虫将不断向光强较强的萤火虫移动,并使得所有萤火虫最终聚集到光强较强的个体附近,从而得到最优解。在算法前期,萤火虫之间的距离较远,可通过式(14)中的固定步长进行搜索,令搜索速度降低。但当算法进入后期,萤火虫之间的距离较小,固定步长易使萤火虫在移动过程中越过最优解,且出现收敛速度慢、在最优解附近来回震荡的现象。因此,文中针对式(14)加以改进,将固定步长改进为与萤火虫之间距离呈正相关的自适应步长。IFA 算法中,萤火虫位置的更新机制如下:
此次所采用SVM 算法[13]的核心思想是通过函数ϕ(x)将非线性数据样本映射至高维空间,从而将非线性问题转化为线性问题。SVM 算法可描述为求解如下所述的数学规划问题:
式中,J为损失函数,w为斜率;b为截距;η为惩罚系数;κq为松弛因子。
ϕ(x)通常为径向核函数:
其中,σ为核函数参数。由上述讨论可知,η和σ对SVM 算法的计算准确性具有较大影响,但对二者的选取通常存在随机性[14-16]。为了提高电力工程项目风险识别的准确性,该文采用IFA 算法对这两个关键参数进行优化,实现了如图2 所示的FCMIFA-SVM 算法。
3 算例分析
为验证所提FCM-IFA-SVM 算法在电力工程项目中的风险识别准确性,从某省电网的电力工程数据智能处理系统中筛选出580 条数据作为训练样本集,并进行了相关的仿真分析。
3.1 IFA算法性能对比
传统FA 算法与文中所提IFA 算法,对SVM 模型中的惩罚系数η及核函数参数σ进行优化的迭代过程,如图4所示。可见IFA算法相比于FA算法具有更快的收敛速度,且其在第13 次迭代计算时已经达到最优值,而传统FA算法在第24次迭代时才开始收敛。
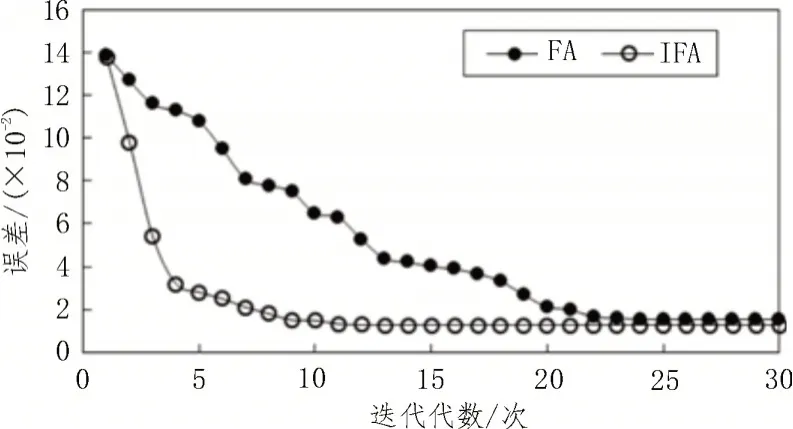
图4 算法迭代过程
FA 算法与IFA 算法的优化结果,如表1 所示。结合图4 可知,IFA 算法的最终误差比FA 算法更小,优化结果更为理想。因此,SVM 模型的惩罚系数η及核函数参数σ分别取为32.8 和0.012。

表1 两种算法对参数优化的结果对比
3.2 风险识别结果对比
进一步将相同数据样本作为输入,对比分析SVM、FCM-SVM 与FCM-IFA-SVM 算法的电力工程项目风险识别准确度,结果如表2 所示。由表可知,FCM-IFA-SVM 算法的识别结果明显优于其他两种算法,其风险识别平均准确率可达92.4%。相比于其他两种算法的识别结果,分别提升了7.1%和2.9%。

表2 不同算法风险识别结果对比
与SVM 相比,FCM-SVM 算法通 过FCM 实现了对具有相同特征数据样本的聚类分析,并降低了样本间的簇类差异对于风险识别结果的干扰,所以其具有更高的风险识别准确度。而FCM-IFA-SVM 相比于FCM-SVM 算法,其利用IFA 来完成对SVM 模型中惩罚系数η与核函数参数σ的优化选取,从而进一步提升了SVM 模型对风险识别的准确度。
3.3 应用效果分析
将本算法应用于10 个电力工程项目的风险识别中,所得结果如表3 所示。表中“1”代表电力工程项目风险识别属于该风险等级,“0”则代表不属于该风险等级。
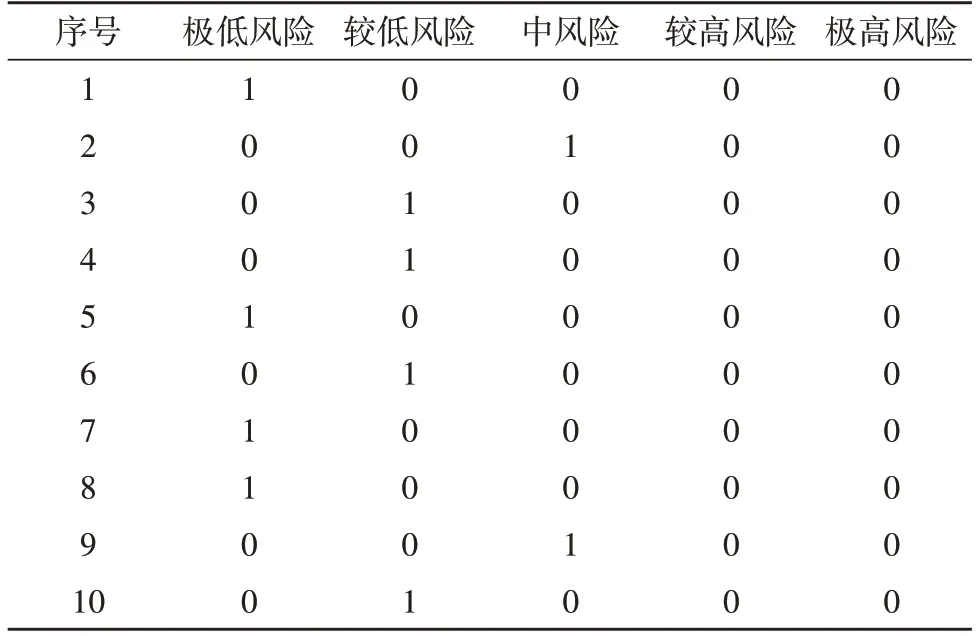
表3 实际电力工程项目风险识别结果
从表3 可看出,10 个电力工程项目中,风险等级为“较低风险”及以下的有8 个,占比达到80%。而项目2 和项目9 为“中风险”,故需加强对这两个项目的监理管控。
4 结束语
利用电力工程中产生的多源数据,该文结合模糊聚类与机器学习算法实现了对电力工程项目风险的精准识别。所提FCM-IFA-SVM 算法通过FCM 降低了样本数据簇类之间差异对风险识别结果的干扰,利用IFA 算法优化了SVM 模型的参数,进而提高了模型的分类性能。与经典算法相比,该文算法的电力工程项目风险识别准确率显著提高。在某省电网实际应用中,其能够准确评估电力工程项目的风险等级,这对于电力工程项目的智能管控而言具有重要的工程意义。但所提算法仅能评估风险等级,无法实现对风险来源的获取及识别,这将在下一步研究中开展。

