基于GBDT 算法的电力工程数据信息分析及预测方法研究

翁海兵，杨 阳，黄 颖

（国网浙江省电力有限公司丽水供电公司，浙江丽水 323000）

随着大数据分析技术的进步以及电力工程数据的爆炸式增长，对数据信息分析与处理的要求也越发严苛[1-3]。为提高电力工程数据分析与预测的精度，国内外学者做了大量的研究工作。早在上世纪90 年代，Freund 便提出以单层决策树(Decision Tree)为基础学习器的自适应提升(Adaptive Boosting,AdaBoost)算法，其可提升数据训练的精度。但该算法仅适用于二分类问题，在此基础上，Friedman 于21 世纪初提出了适用范围更广的梯度提升决策树(Gradient Boosting Decision Tree,GBDT)算法[4-8]。该算法以数据初值为回归树，通过在叶子处得到数据的预测值，其既可用于分类问题，又适用于回归问题。随着集成学习应用领域的愈加广阔，国内学者的研究成果亦层出不穷，且被广泛应用于各种数据预测问题。文献[9]通过将GBDT 与随机森林(Random Forest,RF)算法的优势相结合，预测了一氧化碳含量并取得了较优的效果。而文献[10]在GBDT 算法内融入了多维度特征处理方式，其加入多维数据特征后，大幅提高了模型的预测效率。目前针对电力工程数据信息预测的问题，大多数学者集中于机器学习(Machine Learning,ML)或深度学习(Deep Learning,DL)算法的领域，因此在处理效率与预测精度上仍存在局限性[11-14]。综上所述，文中基于GBDT 算法开展了电力工程数据的分析及预测方法研究。

1 GBDT算法及其改进

1.1 算法原理

GBDT 是机器学习算法中的一种，其为迭代式的决策树算法[15-16]，适用于处理混合数据。该算法的核心是巧妙应用损失函数（Loss Function）的负梯度值，通过不断降低残差的数值来增加数据的真实率，且下一次的决策树均需通过前一次的残差拟合而成。假设样本i的第m次迭代梯度值为：

式中，ηm是第m次迭代的加权系数，f(xi)为数据变量，L为损失函数，yi表示输入数据值为xi时的对应值。因此通过得到相应叶子节点的区域值，便可获得节点的最佳输出值为：

由此得到决策树的拟合函数为：

式中，J为变量个数，I为函数因子。

GBDT 算法在回归时所采用的是平方差损失函数，而在分类时则选择了对数函数，其算法步骤如下：

步骤1：初始化m、j的值，并将二者的值均赋值为1；

步骤2：计算样本i第m次迭代时损失函数的负梯度值；

步骤3：选取特征值，确定最优切分变量与切分点，进而构建回归函数以启动迭代循环操作，迭代循环结束时进行步骤4；否则，继续进行步骤3；

步骤4：计算第m次迭代时的最优输出值；

步骤5：更新拟合函数，若m达到设定阈值，则迭代结束，输出最终结果；否则，转至步骤2。

无约束优化问题通常会转化为最小化目标函数L(θ)的求解，其核心是求得θ的取值并选取初值，然后沿着梯度下降的方向不断迭代以求出近似值。其迭代公式可表示为：

式中，θ为变量，Δθ为变量增加量。将L(θt)在θt-1处展开，可得到：

上述方法从本质上看是一个一阶方程，其核心是求解其一阶导数，但相对误差较大。而当采用二阶函数时，可具有更高的精度及更快的收敛速度，则二阶优化函数为：

对上式求导，且令其值为零，即可得到L(θt)的极小值。从几何的角度来看，则是将二次曲面拟合至当前位置，以获得最优的下降路径，即牛顿法(Newton’s method)。

1.2 正则化改进

模型复杂度与训练饱和度呈正相关，而误差则随着模型复杂度的增加而逐渐增大。所以当样本数量过少或训练次数过多时，就会出现过拟合的现象，如图1 所示。

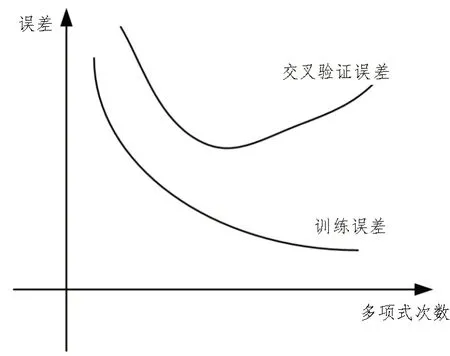
图1 过拟合误差示意图

从原理上讲，应该尽可能地选择可以解释已知数据的简单模型。但为了保证数据的真实性，有时则需要采取更为复杂的模型来拟合复杂数据。因此，该文对模型加以改进：首先在传统GBDT 算法中引入正则化，然后在模型训练的过程中指定回归树，不断拟合残差，最后在损失函数中增加正则项。其理论表达式可表征为：

式中，Ω(fk)为惩罚函数，引入的正则项在每个回归树函数中增加惩罚项。而惩罚项的复杂度与叶子数N、叶节点分数w有关，且惩罚函数可表示为：

式中，γ是叶子数的加权系数。

通过在叶子节点处增加剪枝(Pruning algorithm)操作，经过多次迭代后，模型相邻两次迭代的预测值之和则可表示为：

此时，目标函数可表征为预测值与惩罚函数的相加，即：

2 电力工程数据分析与预测

2.1 数据处理

提前对电力工程数据加以处理，是进行分析与预测的前提。在现场采集到的数据中经常会出现一些特征缺失、存在噪声等信息的数据，其会造成数据处理过程中信息丢失的情况。删除法与填补法是解决数据缺失的常用手段，但是将数据删除会影响其真实性，因此该处理过程中采用了双向综合填补法。该方法类似于单值差补法，即通过计算期望进行填补。对于给定的数据集T，且有：

式中，xi∈Rm，yi∈{0,1}，则得到原始数据矩阵：

其中，m为样本总数，n为特征总数。首先，令i=1，提取相同样本并构造数据矩阵；然后，提取样本数据中第j列数据可得：

计算xij的值为：

综上可得，新的数据矩阵为：

基于数据特征能确定各个参数值，并以此进行数据融合进而感知所有工程数据，最后输出分类回归值。所采用的数据融合框架如图2 所示。

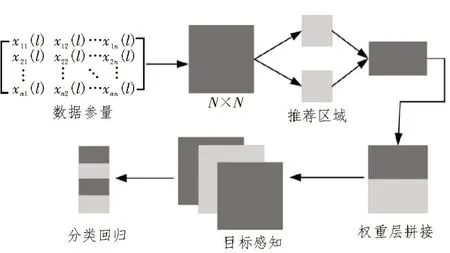
图2 数据感知融合框架

2.2 特征提取

特征提取是降低数据维度的一种方法，其能够得到原始数据的一个子集，并对电力工程数据进行感知与识别，从而建立数据感知模型。对数据特征进行综合分析，是实现数据分析与预测的关键步骤。数据特征融合流程如图3 所示。

图3 数据特征融合流程

通过将数据映射到新的特征空间，再采用主成分分析法(Principal Component Analysis,PCA)对电力工程数据特征加以提取，具体流程如下：

1）收集电力工程数据集，建立数据矩阵X={xij}m×n，并对所有数据进行归一化处理；

2）建立目标损失函数：

3）最小化损失函数，计算协方差矩阵，依据拉格朗日乘子法(Lagrange Multiplier)，建立拉格朗日函数，可表征为：

4）筛选特征向量的主成分，计算贡献率P以获得特性向量主成分，进而重新建立特征矩阵。

对电力工程数据完成特征提取之后，可建立多参量递归图并进行卷积操作，然后再进行最大池化与全拼接操作，并最终输出特征。所建立的卷积神经网络结构流程如图4 所示。

图4 数据卷积神经网络建立流程

2.3 数据训练

在完成数据处理与特征提取之后，还需要对电力工程数据进行训练。具体的训练流程为：首先将所有数据转化为时序参量，从而得到各个数据的回归量；然后，采用GBDT 算法对数据进行训练感知，再对数据加以分类，以获得数据分类结果，并最终建立网络融合模型。在分类流程中，通常以损失量最小来作为迭代结束的依据。且当误差满足预期值时，即停止迭代。预期目标值可表示为：

式中，L(θ)为预期目标函数，采集到的电力工程数据用θ=[θ1,θ2,∙∙∙,θm]表示，该值为神经网络模型输入集合。

数据误差可转化为均方误差函数，具体可表示为：

式中，f(θi)表示当输入预测变量值时所对应的函数值。

3 算例分析

该文选取了三个真实电力工程的数据集用于测试算法，这些数据集来源于某市2021年的配电工程数据库。实验目的在于对比传统机器学习算法与本文所提GBDT 算法的预测精度，从而验证算法的优越性。实验所采用的三个电力工程数据集参数如表1所示。

表1 数据集属性

将每个数据集随机分成两个部分，其中80%的数据作为训练样本，剩余的部分则作为预测样本。算法的基本数据设置如下：根深度为6，最小样本数为500个，而最大迭代次数则为500 次。通过比较算法的运行时间与平均绝对百分比误差（MAPE），进而评价算法的效率。采用两种算法进行测试，其结果如表2所示。

表2 两种算法数据集测试结果对比

从表中可看出，在不同的数据集背景下，当采用GBDT 算法对电力工程数据进行分析与预测时，其预测精度较高、运行时间也更短。

进一步对电力工程造价数据进行分析及预测，通过对比输入与输出值，构建工程造价数据的原始模型。对随机抽取的六组预测样本数据进行分析与预测，得到的预测结果与误差如表3 所示。

表3 电力工程造价数据预测及其误差

依据工程造价行业标准，当误差在5%以内可以作为有用数据。而由表3 可知，数据预测结果均在预期误差范围之内，故可视为有效数据。

4 结束语

针对电力工程数据分析与预测精度偏低的问题，该文提出了基于GBDT 算法的电力工程数据信息分析及预测方法，该算法既适用于分类问题也适用于回归问题。在真实电力工程数据集上进行的数据算例分析结果显示，所提算法的预测精度更高，运行时间也更短，具有良好的工程应用前景。