基于数据融合与智能计算的电网线损管控关键技术研究

黄文学，周麒

（国网甘肃省电力公司古浪县供电公司，甘肃武威 733000）

线损率是反映电力网络规划设计、生产运行与管理经营等各种水平的综合性指标[1-4]。2020 年9月，我国明确提出了2030 年“碳达峰”、2060 年“碳中和”的“双碳”目标。在此背景下，电力运营企业陆续将线损率作为提升企业生产效率、促进节能减排的关键指标。传统模式下，线损率的计算首先需要抽象出电路模型，再借助潮流迭代、等值电阻等方法来完成计算[5-11]。上述方法通过提升数据采样频率、增加电气参数等方式，在计算精度上取得了较大的提升。但随着电网规模的增长，电网的源、负荷及结构均处于动态变化中。而线路建模与线损计算对于人力资源的消耗过大，故无法满足电力生产的效率要求。因此，亟需基于数字化、智能化的手段来对线损管控技术进行升级。

在上述分析的基础上，文中从数据融合的角度出发，通过采集电力网络的电源数据、负荷数据与现有的线损情况，并借助智能网络对线路结构加以描述。同时提取电力网络的运行特征，再模拟其运行状态，从而实现线损的智能化计算。

1 理论基础

1.1 智能计算网络

神经网络是一种常见的智能计算网络。随着计算机性能的提升，多隐藏层的深度学习(Deep Learning,DL)网络也具备了更强的非线性拟合能力。其可模拟电力系统的网络结构，并利用相关参数，实现线损的智能计算。结合线损的计算场景，文中引入基于受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)的深度置信网络(Deep Belief Networks,DBN)[12-15]。该网络计算单元RBM 的基本结构如图1所示。

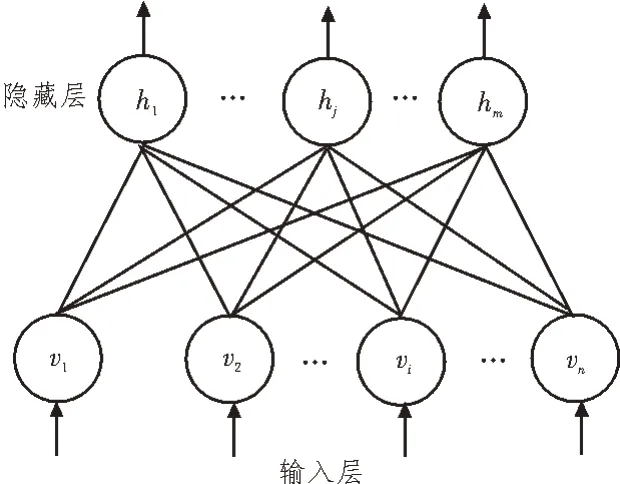
图1 RBM基本结构

图1 中包含由n个输入单元v组成的输入层以及由m个隐藏层单元h组成的隐藏层，且每个单元之间相互连接。所有单元的取值均在[0,1]区间内，则该RBM 的能量值计算如下：

式中，w为RBM 输入层至隐藏层间的连接权重，a为输入层的偏置，b为隐藏层的偏置。RBM 基于参数θ确定网络能量的概率分布函数为：

相较于普通的神经网络，RBM 是一种可自编码的非监督网络，其在特征提取上具有更高的效率。

RBM 使用概率分布的似然函数作为训练过程的损失函数，以避免网络训练出现过拟合现象，即：

与普通的BP(Back Prpagatin)神经网络不同，RBM 在求解参数θ时通常采用梯度上升法(Gradient ascent algorithm)，即求解式（4）对网络参数的偏导数，则有：

对于参数w、a和b，其各自的偏导数为：

1.2 电力数据融合模型

在实际运行过程中，电网的运行方式并不相同，故需结合其运行方式建立融合式数据模型。基于电路理论的叠加定理(Superposition Theorem)与牛顿拉夫逊计算法(Newton-Ralfsnn’s method)的输电系统等效示意图，如图2 所示。

图2 线损计算的等效模型

图2 中，Igm为电网中的源，-Id(n-m)是电网中的负荷。基于阻抗形式，列出图2 的节点电压方程为：

考虑到网络中电压源单独作用、电流源单独作用、电源相互作用、节点注入功率与网络参数变化等因素的影响，图2 中的网络整体损耗如下：

其中，q为电网中源的总个数，S为节点的视在功率。基于数据融合的思想将线损模型映射至DBN网络，具体如图3 所示[16]。

图3 基于DBN的线损智能计算网络

根据图3 构造DBN 网络的输入矩阵X与输出矩阵Y，分别表示为：

式中，P为节点的有功功率，Q为节点的无功功率，U为节点的电压，ΔP为该线路的线损。

2 方法实现

2.1 实验设计

为了评估该文算法在进行线损计算时的精度，选取了 某地区35 条10 kV 线路 在2021 年11 月1 日—11 月30 日共30 天的运行数据进行模型性能验证。在采集数据时，以5 min 为时间粒度，对照电网的等值模型图采集重要节点的流入功率、无功功率与节点电压等参数。

在评估模型性能时，选择了平均绝对百分比误差(MAPE)与均方根误差(RMSE)来作为指标，二者的计算方法如下：

在进行线损计算时，文中根据不同线路的等值模型图确定DBN 网络的输入参数。当某线路的等效节点为n时，其网络的输入层节点个数为3n，且分别为节点n的有功功率、无功功率及电压。具体的网络结构设置如表1 所示[17]。

表1 网络结构参数

根据网络规模合理选择训练网络的计算机软硬件环境，算法仿真时的软硬件环境如表2 所示。

表2 算法仿真软硬件环境

2.2 系统测试结果

由上文可知，此次需完成35 个DBN 网络的训练，但每个网络的结构均不相同在，因此并未直接给出网络训练所使用的学习率、动量与误差阈值等参数，而是通过采取在线学习的方式训练并确定这些参数。下面以某条10 kV 的线路为例，介绍网络的训练过程。

此外，在对每条线路进行训练前，还需测试该线路所对应模型的学习率Alpha、批量规模Minisize 以及是否需要引入Dropout 机制，具体如图4 所示。

图4 模型在不同超参数下的训练结果

由图4 可知，Alpha、Minisize 及Dropout 机制均会影响网络中损失函数在训练过程中的收敛速度。从图4(a)可以看出，随着Alpha 的增大，损失值函数的收敛速度不断加快。但考虑到过大的学习率会影响网络对于最优值的搜索，所以将该网络最终的学习率设置为0.05。由图4(b)可知，损失值函数在不同Minsize 下的收敛曲线并不相同，且不是线性递增或递减的关系。由于Minisize 还与网络的传播权重及偏置的更新率有关，故将该网络最终的批量规模设置为672；图4(c)显示出，引入Dropout 机制后网络损失值的误差曲线收敛更快，并可有效降低网络出现过拟合的概率。因此文中对所有线路进行模型训练时，均引入了Dropout 机制。模型经过训练后，使用1/5 的数据作为测试集来对模型的预测性能进行测试。为了评估模型的性能，使用与表1 相同结构的BP 网络进行对比。二者对于35 条线路的实际线损部分预测结果如表3 所示。

表3 两种算法的线损预测结果

从表3 中可以看出，相较于BP 网络，该文算法对每条线路的线损预测结果与线路在该时间段的实际值均更为接近。而两种模型的性能指标统计信息如表4 所示。

表4 模型指标的统计信息

由表4 可知，该文算法的MAPE 与RMSE 指标较BP网络均有显著提升。其中MAPE提升了4.019%，而RMSE 降低了74.40%。由此可见，线损的预测效果有了明显改善。

3 结束语

该文对电网运行线损管控中的关键技术进行了研究，并基于数据融合的思想，借助深度置信网络构建了线损智能计算网络。该网络相较于传统的等值电阻、潮流法等提高了计算效率，而与BP 神经网络相比则提升了计算精度。未来随着电力企业数字化转型的推进，所提算法将有更广阔的应用前景。