基于Fair 函数神经网络的厚度传感器输出特性分析
张艳肖,李守智,张江江,曹小鸽,徐 微
(1.西安交通大学城市学院,陕西西安 710018;2.西安理工大学自动化学院,陕西西安 710048)
在印刷、化工、建筑等领域,广泛需要厚度检测,国内外相继出现多种厚度检测技术,常见的有基于各种射线、超声波、涡流、太赫兹时域光谱等[1-4]。电容传感器具有价格低、动态响应快、分辨率高等优点,将电容式传感器用于厚度测量,相比于其他方法成本低、功耗小,而且对人体不会造成伤害。电容传感器因受到边缘效应、寄生电容及操作误差等因素的影响,存在较大误差,制约了其测量精度。为了减小误差,需要对传感器输出特性进行补偿,常用的方法有最小二乘法[5-6],支持向量回归算法[5-6]及人工神经网络[9-10]算法,最小二乘法和神经网络是基于误差平方和下降的计算来求最优解,对拟合数据准确性要求较高,不具备抗击坏数据的能力。然而拟合数据来源于现场测试,随机误差和过失误差可能同时存在,将导致补偿效果变差。针对以上问题,该文引入抗差理论中的Fair 函数,提出一种基于Fair 估计函数BP 神经算法,使得电容式测厚传感器测量精度得到有效提高。
1 电容传感器测量原理
电容传感器原理如图1 所示,电容传感器的初始电容值表达式如式(1)所示:
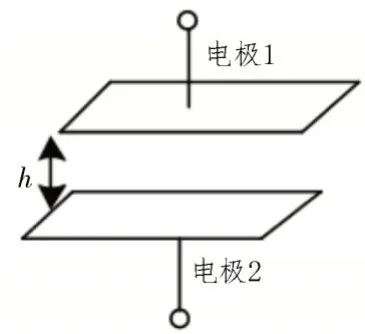
图1 电容传感器结构
式中,ε0为真空的介电常数,ε1为待测介质的介电常数,A为电容传感器极板的有效面积,d0两极板之间的距离,可知电容传感器的电容值变化由以上几个参数共同决定[11-13]。将平行极板固定在待测材料两端,被测材料厚度变化时引起传感器电容的变化。根据高斯定理,传感器电容Cx与材料厚度θ之间的关系如式(2)所示:
在实际工程应用中,传感器受周围环境、目标个体差异和边缘效应等多方面影响,不可避免的存在测量误差,其输出电容与材料厚度之间难以满足上述函数关系,为了提高测试精度,系统需要对测量数据进行回归分析,得到材料厚度与传感器电容之间的关系,并对未知目标进行估算。
2 神经网络分析
2.1 基于最小二乘法BP算法的不足
BP 算法是按误差逆传播算法训练的多层前馈神经网络,是目前应用最为广泛的神经网络模型之一。网络结构为输入层、隐含层和输出层,如图2 所示。从输入层接收外界数据开始,将数据信息正向传播给隐含层,经过处理后在输出层输出结果。网络训练的实质是误差e再向后传递的同时调整权值,以使实际输出接近预期输出值,传统的权值由最小二乘法求得,取误差函数为:
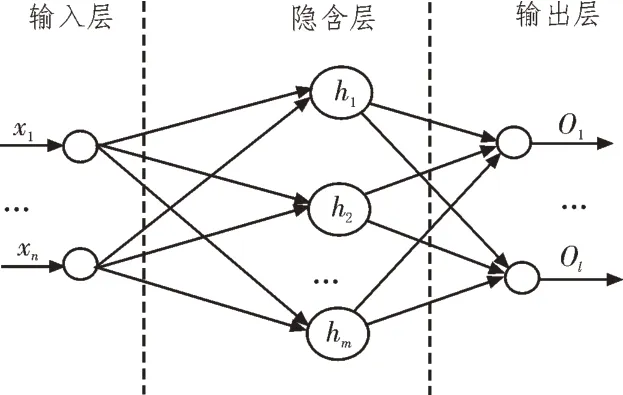
图2 BP神经网络
误差函数是单调函数,最小二乘法适用于测试数据仅有随机误差,且误差服从正态分布[14]的情况,而在实际工业操作过程中测量误差中还可能存在过失误差,过失误差往往没有规律可循,这将导致神经网络预测不准确。
2.2 基于Fair估计函数
为了减小测量误差对测厚电容传感器测量结果的影响,将鲁棒的估计理论应用于神经网络。鲁棒的估计方法通过构成一种无偏学习函数,在一定偏离理想条件下对这种过偏不敏感或者呈现比较低的敏感度[15-16]。根据鲁棒估计理论影响函数的定义,影响函数I(ζ) 正比于数据校正中误差函数的导数,鲁棒估计的影响函数必须有界。当ρ(e)为鲁棒的误差函数时,需要满足:
Fair 估计的影响函数可表示为:
其中,cF是一个调节常数,在标准高斯分布下,取1.399 8[17]。图3 为误差与影响函数之间的关系,可知随着e增大,最小二乘法(LS)函数无界,不具备鲁棒性。而Fair 估计的影响函数随着误差的增大逼近某一常数,满足鲁棒估计理论的条件。并且Fair 估计函数是凸函数,有利于神经网络的优化计算,过失误差判别能力较强,可以利用它求得最优解,提高传感器的测量精度。

图3 不同的影响函数与误差的关系
3 基于Fair估计函数的BP学习算法
基于Fair 估计函数是鲁棒的学习算法,该文采用该算法对神经网络进行训练。假设输入层训练样本X=[x1,x2,…,xn],隐含层输出H=[h1,h2,…,hm],实际输出O=[o1,o2,…,ol],期望输出Y=[y1,y2,…,yl]。输入层到隐含层的权重3wij,隐含层到输出层的权重为aj,隐含层到输出层的偏置为bk,学习率为η,激励函数选择sigmoid 函数:
隐含层的输出为:
输出层的输出为:
当网络输出与期望输出不等时,存在误差:
由前文分析可知,基于Fair 估计函数可以减小测量误差对神经网络输出的影响,基于Fair 估计误差函数为:
采用梯度下降法对隐含输入层到输入隐含层权值进行更新:
隐含层到输出层权值更新为:
偏置更新为:
4 结果对比分析
该文采用FDC2214 电容式传感器,测量单张及多张重叠的标准双铜纸张的厚度进行实验验证。测量前对纸张进行干燥,减小纸张中水分对测量精度的影响。表1 给出了两组传感器响应的特征值,其中,第2 组数据中含有10%的过失误差。
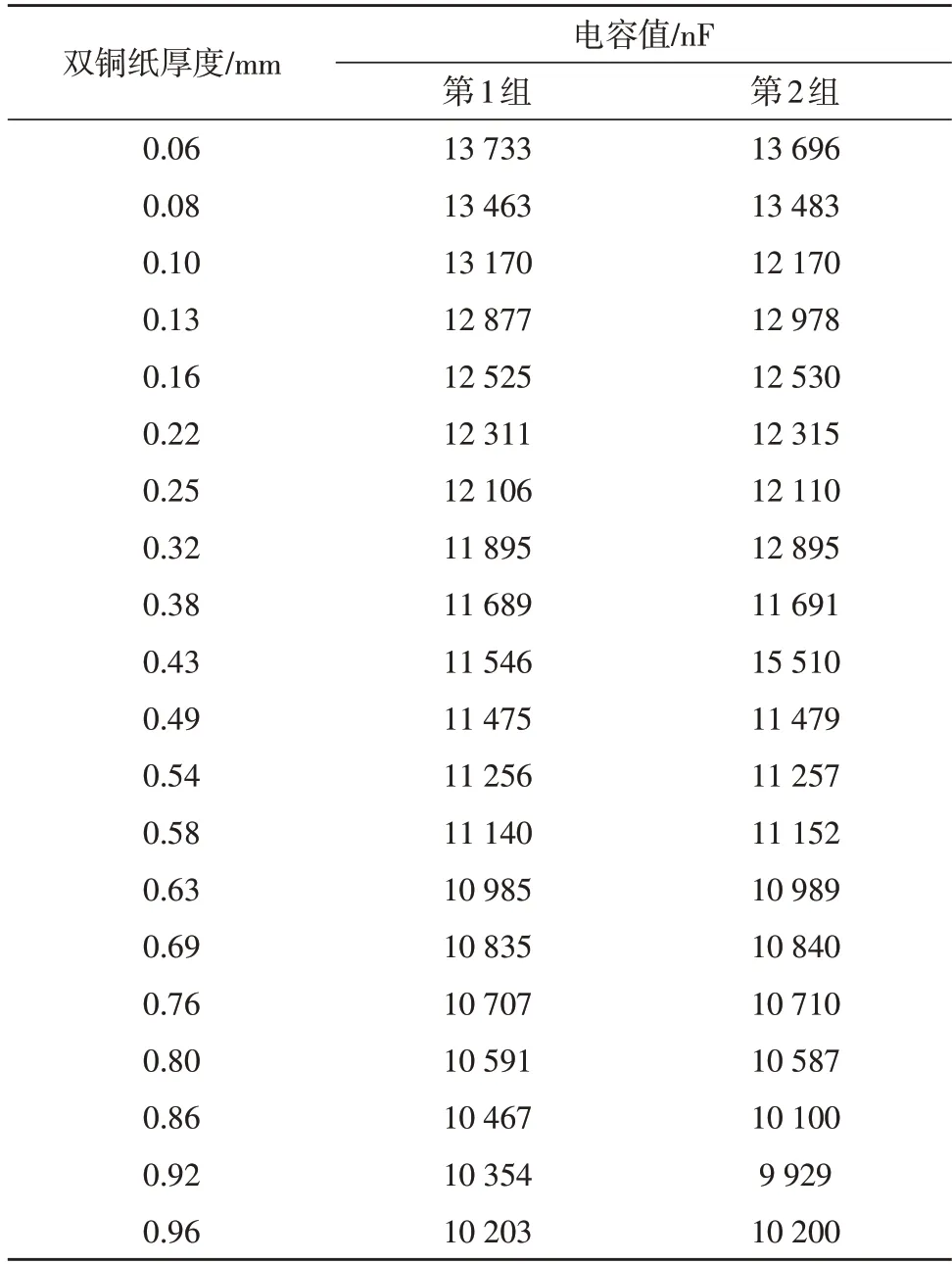
表1 FDC2214传感器在不同厚度纸张下的特征值
将传感器的输入厚度作为网络的输入,厚度经传感器后的对应输出电容值作为网络期望输出。利用Matlab 建立BP 网络的模型及参数设置,输入训练样本,学习误差函数分别为基于最小二乘法(LS)和Fair 估计函数,将参数设置为一样η=0.3,对网络进行若干次学习训练,连续调整网络的权值和阈值。测量数据中,不含过失误差拟合结果如图4 所示,拟合误差如图5 所示,当正常测量不含过失误差时,基于最小二乘法(LS)和Fair 估计函数的BP 学习算法拟合结果基本接近。图6 为拟合数据中含有过失误差拟合结果,利用最小二乘法(LS) BP 学习算法造成过失误差误判,基于Fair 估计函数BP 学习算法拟合结果更接近于真实值,拟合误差如图7 所示。采用均方根误差(MSE)评价拟合效果,表2 给出拟合后均方根误差比较结果,当拟合数据中含有过失误差时,基于Fair 估计函数BP 学习算法拟合效果更优,具有较强的鲁棒性。
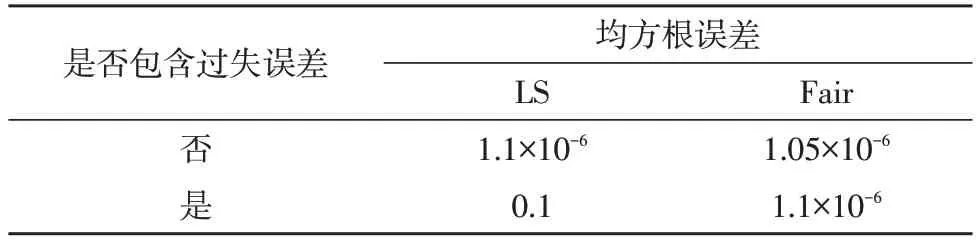
表2 均方根误差比较结果

图4 不含过失误差拟合结果
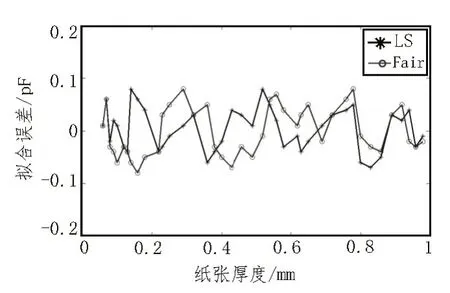
图5 拟合误差

图6 含过失误差拟合结果

图7 拟合误差
5 实验验证
将上文分析得到的基于Fair 估计函数BP 学习算法写入STM32 单片机程序中,测量双胶纸纸张厚度,测试结果如表3 所示。结果表明,厚度传感器能准确测量纸张厚度,测量相对误差小于1.5%。
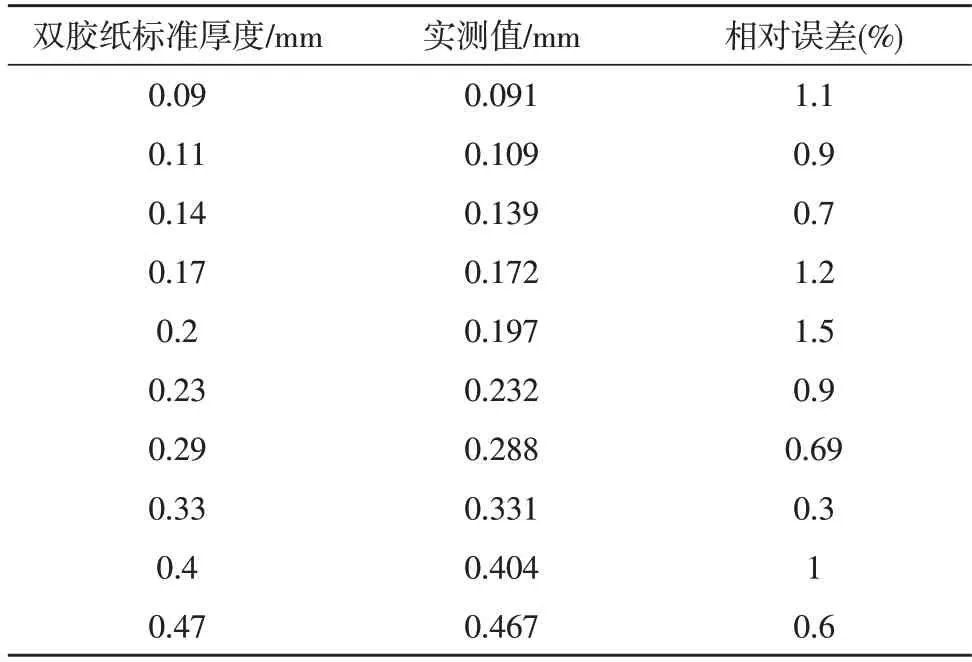
表3 实测结果
6 结论
该文提出基于Fair 估计函数的BP 学习算法并应用于电容传感器厚度测量,当训练数据中含有过失误差和随机误差时,拟合精度明显高于传统基于最小二乘法BP 学习算法。实验结果表明,该算法应用于厚度传感器能准确测量纸张厚度,测量相对误差小于1.5%。

