合理应用变式 提升复习效益——以“数列通项的求法”教学为例

陈荣庆

⦿ 江苏省泰兴市第三高级中学

进入高三,复习就是课堂教学的主旋律.高三复习是对之前所学知识的一次深入、全面、系统的梳理,是对所建构的数学知识体系的进一步优化.数学是一门逻辑性较强的学科,只有建构完善的知识体系才能有效提高数学迁移能力,进而提高分析和解决问题的能力.不过,在传统教学中,复习课大多以“题海战术”为主,教师试图通过“以练代学”的方式来提高成绩,致使学生学业负担过重,课堂上出现抵触复习课的现象,使得复习课的价值难以发挥.同时,“刷题”占用了学生宝贵的独立思考和合作探究的时间,使得学生对知识的理解仅限于表面,影响知识的系统化建构和解题能力的提升.基于此,教学中有必要突破传统“讲授+练习”教学模式的束缚,为学生营造一个探究的学习环境,提高学生参与复习活动的积极性,提高复习效益.变式教学作为一种重要的解题教学方式,在复习课中有着重要的应用.复习课上,通过有效的变式训练可以帮助学生领悟数学知识之间的内在联系,提炼蕴含其中的数学思想方法,掌握问题的本质特征,培养发散、化归、逻辑、创造等思维品质,提高复习课的教学收益.

笔者以“数列通项的求法”专题训练为例,合理设计变式,让学生在“变与不变”中领悟数学的本质,积累解题方法,提高课堂教学效能.

1 合理应用变式,揭示数学实质

数学题目是千变万化的,若教学中一味地让学生“刷题”,不仅会增加数学的乏味感,而且会增加学生的学业负担,影响教学效果.为了改变这一局面,教师可以尝试引入变式,让学生在“变与不变”中领悟数学的本质,提高举一反三的能力.

例1设{an}是等差数列,且a1=3,a2+a5=36,则{an}的通项公式为______.

例2在等比数列{an}中,已知a1=3,a6=96,则{an}的通项公式为______.

变式1设{an}是等差数列,已知a1a2=35,2a4-a6=7,则{an}的通项公式为______.

变式2Sn是等比数列{an}的前n项和,若S4,S3,S5成等差数列,则{an}的通项公式为______.

设计意图：例1和例2难度不大,主要考查学生的基本知识掌握情况,运用等差数列和等比数列的相关公式即可获解.对于一些基础题,可以鼓励学生尝试应用一些简便的方法来分析和解决,进而由“驾轻就熟”向“熟能生巧”转变,提高解题能力.变式1和变式2较例题相比难度略有提升,这样既可以促进知识的深化和技能的提升,又能让学生体会到变式教学的“万变不离其宗”,提高举一反三的能力.

2 合理应用变式,提升训练效率

数学题的解法大多不唯一,观察的角度不同,思考的方向不同,其解题过程也会有所不同,而选择何种方法解决问题既可以检测学生的基础知识掌握程度,又能了解学生的思维发展水平及数学素养.在日常教学中,教师要鼓励学生从不同角度去分析,探寻不同解决问题的方法,以此拓宽视野,积累丰富的解题经验,为认知结构的优化和解题能力的提升添砖加瓦.

例3已知数列{an}的前n项和Sn=n2+2n+1(n∈N*),则an=______.

变式设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=______,S5=______.

以上例题较前面例题和变式题来讲,其难度略有提升,教师预留充足的时间让学生独立思考,并鼓励学生应用不同的方法解决问题.学生的思路形成后,教师让学生进行组内交流,并引导学生归纳总结通性通法,以此达到夯实基础,提升素养的目的.

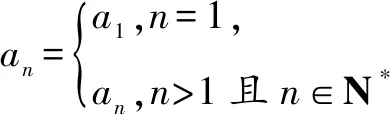
在解题教学中,教师要重视通性通法的提炼,这是提高学生解题能力的关键.不过,笔者在解题教学中发现,学生在解题时常出现“重技巧,轻通法”的现象.在高三复习教学中,部分师生受技巧中“巧”的诱惑,片面地认为应用解题技巧是提高解题效率的法宝,使得学生为了追求技巧,忘记了解题的根本,影响了解题效果.事实上,在高三复习教学中,淡化技巧、强调通法才是提高学生解题能力,发展学生数学思维的正道.

3 合理应用变式,突破重难点

课堂教学中,每节课都有一些重难点内容,对于这些重难点内容,教师常常是反复讲、重复练,但是教学往往却不如人意.究其原因就是学生对知识的理解还停留于表面,并未抓住问题的本质,题目略加变化就显得束手无策.因此,在强调重点、突破难点的过程中,教师可以采用重点讲授和变式探究相结合的方式来展开,这样不仅可以达到巩固知识、强化技能的效果,而且可以促进学生思维的生长和能力的提升.同时,通过适度的变式训练,可以避免机械训练所带来的枯燥感,提高学生探究的积极性,让学生在题解中获得发散思维的培养和数学能力的提升.

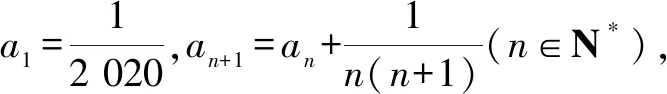
例5已知数列{an}满足a1+3a2+……+(2n-1)an=2n.

(1)求数列{an}的通项公式;

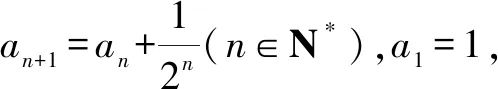
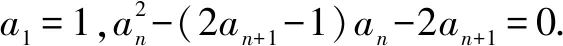
(1)求a2,a3;

(2)求数列{an}的通项公式.

设计意图：以上例题及变式题较前面两个层次的问题来讲,难度有所提升.这样由浅入深、由易到难的梯度练习可以让学生的思维螺旋上升,逐渐提升解题信心和解题能力.在日常教学中发现,有些学生遇到较为繁琐、陌生的题目时容易出现畏难情绪,继而失去解题信心,影响解题效果.基于此,在日常教学中,教师应重视专项训练,引导学生学会“套路化”的解题方法和思路,让学生能够根据题目特点快速找到解题的突破口,形成解题思路.例如,对于以上问题,可以分为两种情况来分析.一是针对满足an+1=an+f(n)且数列{f(n)}可以求和的递推数列问题,可以采用累加法来解决;二是针对an+1=anf(n)且数列{f(n)}可以求积的递推数列问题,可以采用累乘法来解决.分析至此,学生可以根据题目特点选择合理的解题方法,以此实现化繁为简、化陌生为熟悉的效果,突破思维障碍,高效解决问题.

数学题目虽然千变万化,但是变化中往往会有一些不变的规律和方法.在复习教学中,要重视常规解题方法的积累,培养惯性思维,让学生在解题时能够根据题目特点形成“条件反射”,快速找到解题思路.在以上教学活动中,教师结合教学实际合理设计变式问题,大大提升了学生参与课堂的积极性,增强了学生的解题信心.另外,在解题过程中,教师根据题目的难易程度设计了不同的学习活动,让不同层次的学生都能有所发展、有所成长.

总之,在复习教学中,教师既要重视基础知识的复习和巩固,也要重视通性通法的提炼与积累,善于通过针对性的练习帮助学生形成解题套路,以此让学生在面对相似的问题时能够快速形成解题策略,将培养学生的逻辑思维能力落到实处.Z