基于PSO-RF的扩底灌注桩极限抗拔承载力预测

张博航，薛新华

(四川大学水利水电学院,四川 成都 610065)

0 引言

桩基是一种适用范围广同时承载能力较高的基础。伴随着城市化进程的快速发展,建筑物对桩基竖向承载能力提出了更高的要求。成桩方法不断发展的同时桩身材料与桩身形状也在不断丰富以适应不同的工程需要。在地下水位较高与上部水平荷载较大的情况下,建筑物基础需要具备一定的抗浮能力。为提高桩基础抗拔承载能力,工程建设领域开始广泛运用异截面桩。扩底灌注桩是一种桩体质量可靠的异形截面桩,拥有较好的抗拔承载能力[1]。传统方法测试桩的抗拔承载能力存在一些不足(例如耗时很长且价格昂贵),在某些特殊情况下很难大规模开展静荷载测试。因此,提出一种基于少量静荷载测试准确获取特定地区桩体极限抗拔承载力的方法是很有必要的。

伴随着计算机技术与大数据处理技术的快速发展,机器学习作为拥有高泛化能力的数据处理方法应运而生。机器学习方法精度较高且计算速度快捷,近年来在工程建设领域取得了丰富的研究成果。例如,人工神经网络(ANN)、支持向量机(SVM)、遗传算法(GA)等方法被广泛运用于预测桩基竖向极限承载能力与不同类型土壤中的桩体沉降。刘顺[2]利用优化BP神经网络建立了单桩竖向极限承载力的预测模型;李平[3]将神经网络运用于高层建筑桩基承载力预测中,并建立了预测超长桩竖向极限承载能力的预测模型。但机器学习方法依然存在不足,如预测模型内部计算超参数难以选取、计算模型陷入局部极值、计算速度较慢以及出现过拟合问题等。为解决机器学习方法的不足,常用群体智能算法对计算模型进行优化,利用自适应变异与均衡惯性权重方法进行参数寻优[4]。目前针对扩底灌注桩极限抗拔承载能力的研究较少,同时尚未有准确计算桩体极限抗拔承载力的方法。本文利用PSO算法对RF算法进行参数优化(即PSO-RF算法),建立了多因素影响下扩底灌注桩极限抗拔承载能力的预测模型。预测结果与实际测量结果相比,数据之间的吻合度很高,模型的决定系数R2为0.974且100%的数据点误差在20%以内。通过PSO-RF方法建立的预测模型对快速确定扩底灌注桩极限抗拔承载力以及提高工作效率有重要意义。

1 PSO-RF算法

1.1 粒子群优化(PSO)算法原理

PSO算法[5]其思路是初始化一群随机粒子,然后通过反复迭代计算找到全局最优解。算法主要步骤如下:

1)粒子群初始化。采用混沌映射方法确定d维空间上粒子群初始化后的速度区间及搜索空间、确定随机粒子最初的速度与位置,均匀分布粒子种群初始位置。

2)确定粒子个体极值。计算每一个粒子的适应值fi,然后同个体极值Pi进行比较,若fi≥Pi,则用fi代替Pi。

3)确定粒子群全局极值。比较全局极值G与适应值fi,若fi≥G,则用fi代替G。

4)更新粒子的位置与速度。随机粒子的速度和位置更新公式如式(1),式(2)所示。

(1)

(2)

为了避免粒子群在有限迭代次数下出现早熟收敛情况,本文采用动态自适应惯性权重平衡算法的全局搜索能力与局部搜索能力,从而找到全局最优解。动态自适应惯性权重的计算方法如式(3)所示:

(3)

其中,f为粒子当前的适应度值;w为惯性权重。

5)判断PSO算法是否终结。若满足条件则结束算法并输出结果,否则返回步骤2)。

1.2 RF算法原理

RF算法属于机器学习中的集成学习方法,本质上是一种包含若干决策树的强学习模型,主要运用于解决分类与回归问题。该算法将随机形成的决策树组合形成一个分类预测能力更加高效的强分类器,根据少数服从多数的原则,结合所有决策树的预测结果确定最终的预测结果。算法有效解决了决策树决策流程单一的问题,并且不同决策树训练过程能够高度并行,增强了模型的泛化能力与计算速度。算法具体步骤如下[6]:

1)从数据总集中采用随机重复抽样的方式抽取m个数据组成训练集,剩余的数据为模型测试集。2)训练集利用分类回归算法训练为若干并行的决策树。3)重复步骤1)和2)直到决策树数量T满足算法要求。4)取决策树预测值的平均值作为回归问题最终的预测结果。算法具体流程如图1所示。

1.3 PSO-RF算法原理

研究表明,决策树数量n、决策树最大深度p对RF模型预测精度与计算速度的影响很大。参数合理取值可缩短模型计算时间、提高预测精度。传统RF算法需要对超参数进行大量试错计算,计算效率较低且容易出现过拟合情况,模型可靠性有待优化。而利用群体局部信息和全局信息进行指导搜索的PSO算法具备较优秀的参数选择能力。基于此,本文提出了将PSO与RF混合的预测模型。PSO-RF算法建立预测模型主要包括三个阶段,即数据预处理、超参数迭代优化、预测模型训练及测试。首先算法会将原始数据进行归一化处理以提高模型的精度与计算效率。随机选取80%的数据用于模型训练,剩余数据对模型进行测试。利用粒子群优化算法对超参数(决策树个数n和决策树最大深度p)进行优化调整。算法指定初始参数后进行迭代计算,确定每轮迭代后粒子的局部最优与全局最优值。当迭代次数最大且粒子适应度值不变时,得到最优的超参数。模型运算流程如图2所示。

2 数据库建立

2.1 样本数据

本文收集了已发表文献中40组上海地区建筑工程项目的扩底灌注抗拔桩现场试验数据作为建立PSO-RF预测模型的数据基础[7]。为建立一个稳健的预测模型,输入参数的选择至关重要。本节利用统计分析软件(Statistical Product and Service Solutions, SPSS)对数据库中6个参数与桩体极限抗拔承载力之间的相关性进行了分析,结果如表1所示。表1中,V1—V7分别表示桩体扩大段上部土层的抗拔阻力、桩侧土体摩阻力加权平均值、抗拔桩直杆段的长径比、扩底部分直径与直杆段直径之比、扩底段桩身直径、扩底段桩长和扩底抗拔桩极限抗拔强度,#表示两参数间的相关性在0.01级别上显著(单尾)。根据肯德尔相关性分析结果,桩体扩大段上部土层的抗拔阻力、扩底部分直径与直杆段直径之比和扩底段桩长等参数之间的相关性较高,分别为0.325,0.278和0.277。将相关程度不同的变量代入计算模型能够提高模型的准确度。根据肯德尔相关性分析结果(见表1),本文将桩体扩大段上部土层的抗拔阻力(kPa)、桩侧土体摩阻力加权平均值(kPa)、抗拔桩直杆段的长径比、扩底部分直径与直杆段直径之比、扩底段桩身直径(m)、扩底段桩长(m)6个参数作为模型的输入变量,将扩底抗拔桩极限抗拔承载力(kN)作为输出变量。

表1 肯德尔相关性分析结果

2.2 评价指标

为了检验所提模型的准确性,决定系数(Coefficient of Determination,R2)、变异系数(Coefficient of Variation, COV)、平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)、平均百分比误差(Mean Absolute Percentage Error, MAPE)等统计指标来评价实测值和预测值之间的误差。其中,标准差与平均值的比值称为变异系数,均方根误差是预测值和实际值的差值,平均绝对误差是预测值和实际值之间的平均误差,平均百分比误差是评价模型优化程度的指标,以上四个评价指标数值越小,则说明模型的性能越好。决定系数表示模型试验值与预测值的拟合情况,其数值越接近于1,则说明拟合情况越好,预测值越接近实际值。以上指标公式表达如式(4)—式(8):

(4)

(5)

(6)

(7)

(8)

为避免数据库中数据的量纲不同对模型结果造成影响,本文在Matlab平台中采用Mapminmax函数将数据归一化处理至[0,1]。归一化原理如式(9)所示。

(9)

其中,X为数据库原始数据;Y为归一化后结果。

3 模型预测结果分析

3.1 PSO-RF模型

本文提出了PSO-RF混合预测模型。首先利用RF算法提出了一种扩底灌注桩极限抗拔承载力预测模型,在构建决策树时不进行裁剪,避免抑制决策树生长。然后采用粒子群优化算法对模型进行优化,结合粒子群优化算法通用性强且易于实现的特点快速确定RF模型合适的超参数取值。

采用PSO算法确定RF模型的最优超参数。通过计算所得到的最优的决策树个数n和决策树最大深度p分别为196和5,在此基础上建立的扩底灌注桩极限抗拔承载力预测模型的结果及其误差统计情况如图3所示。由图3(a)可知,PSO-RF模型的R2,COV,MAPE,RMSE和MAE值分别为0.976,0.091,0.072,159.48和125.17。通过对比训练集与测试集的统计指标,发现测试集的各项统计指标与训练集的差异很小,说明模型并未出现欠拟合或者过拟合现象。从图3(b)中可以看出,70.9%的数据点误差在5%以内,80%的数据点误差在10%以内,100%的数据点误差在20%以内,这表明PSO-RF模型的预测性能较好。

3.2 与其他模型的对比分析

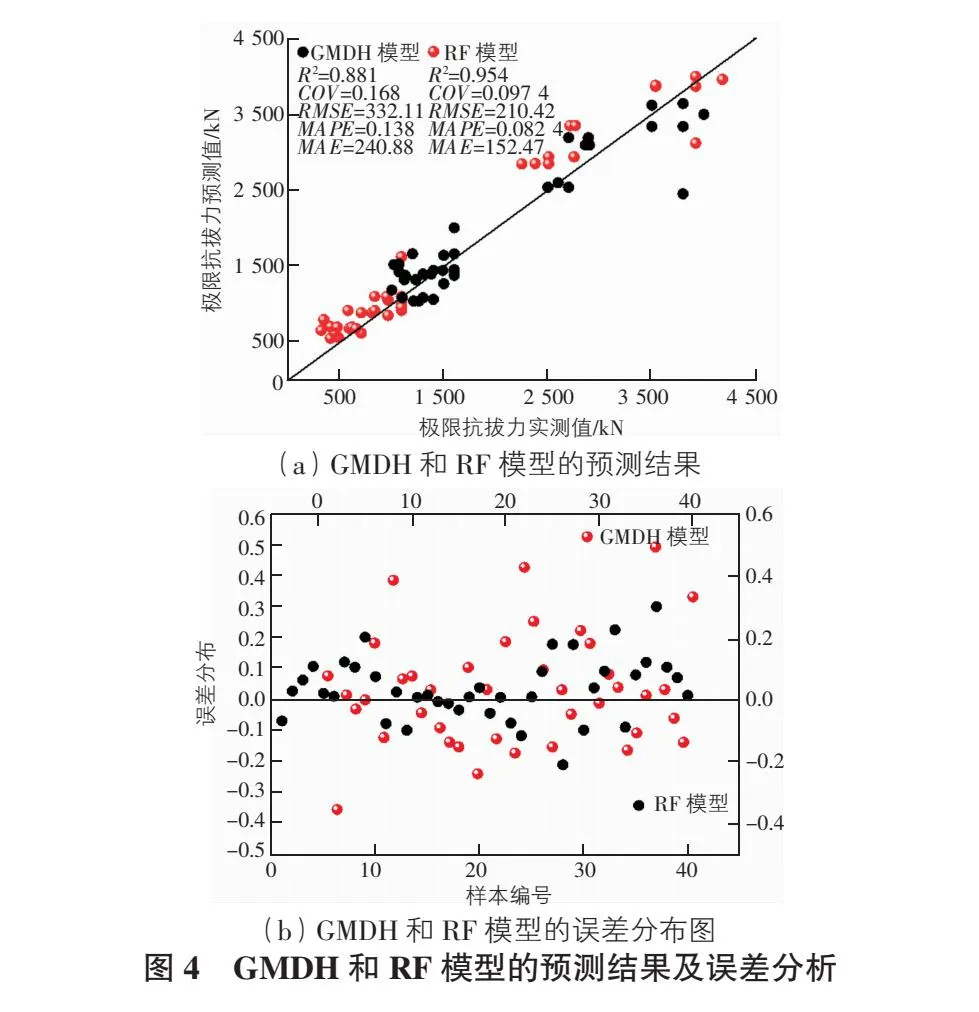
为了验证本文所提模型相较于其他预测模型的优越性,同时验证PSO算法对RF算法的优化情况。本文将PSO-RF模型与基于RF和GMDH建立的模型进行对比,如图4,表2所示。从图4(b)和表2中可以看出,RF模型的预测结果与测量结果比较接近,决定系数为0.955,51%的数据点误差在5%以内,72%的数据点误差在10%以内,95%的数据点误差在20%以内。而GMDH模型预测精度较差,决定系数仅为0.88,50%的数据点误差在10%以内,80%的数据点误差在20%以内。通过试错法确定超参数取值的RF和GMDH模型均出现了程度不一的过拟合现象,即模型在训练集上的预测精度高于测试集。过拟合现象导致模型精度与泛用性较差。综合来看,RF模型优于GMDH模型,其R2,COV,MAPE,RMSE和MAE值分别提升了8.3%,40.2%,39.9%,50.5%和45.6%。将PSO-RF模型与RF模型进行对比,发现PSO-RF模型的R2,COV,MAPE,RMSE和MAE值相较于RF模型分别提升了2.3%,7.1%,13.2%,3.0%和4.5%,且PSO的参数寻优有效解决了RF算法中通过试错法确定最优超参数准确度较低的问题,有效提高了模型的计算效率与准确性。计算结果表明PSO-RF混合模型有最优的预测精度与泛用性,同时证明了PSO-RF混合算法超参数迭代寻优的可行性。

表2 与其他模型的对比分析

3.3 实际工程验证

为验证本文所提方法在实际工程中的适用性,选取虹桥商务区核心区一期3号地块南块新建项目的扩底灌注桩抗拔静荷载试验进行分析比对,PSO-RF模型的预测结果与实际测试结果的误差在5%以内,证明了该方法的工程适用性。具体结果如表3所示。

表3 虹桥商务区核心区一期3号地块南块扩底灌注桩抗拔静荷载试验与模型预测值比较

4 结论

1)本文利用PSO优化RF算法,以40组扩底灌注桩极限抗拔承载力试验数据作为模型训练和测试的基础,将桩体扩大段上部土层的抗拔阻力、桩侧土体摩阻力加权平均值、抗拔桩直杆段的长径比、扩底部分直径与直杆段直径之比、扩底段桩身直径、扩底段桩长6个参数作为输入变量,扩底灌注桩极限抗拔承载能力作为输出变量,成功建立了扩底灌注桩极限抗拔承载力的预测模型。PSO-RF模型的R2,COV,MAPE,RMSE和MAE值分别为0.976,0.091,0.072,159.48和125.17。该模型能够根据桩体几何参数和工程现场土体性质准确预测出扩底灌注桩极限抗拔承载力,减少工作量的同时降低成本,为地下建筑工程的抗浮设计提供参考。

2)将PSO-RF混合模型与RF模型、GMDH模型进行对比,发现PSO-RF混合模型略优于RF模型且二者远优于GMDH模型。PSO-RF模型的R2,COV,MAPE,RMSE和MAE值相较于RF模型分别提升了2.3%,7.1%,13.2%,3.0%和4.5%,表明PSO-RF混合算法有效优化了传统RF算法的超参数选取过程,提高了预测模型的计算效率与精度。