电力市场环境下水电站优化调度运行决策研究

王 伟 刘小靖

一、引言

随着我国新一轮电力体制改革的全面铺开，售电市场改革、增量配网改革、现货市场、输配电定价、辅助服务市场等多交易品种协同发展。在新的电力现货市场环境下，水电企业经营的关键目标就是如何在考虑各种约束的前提下使盈利最大化。在垄断经营模式和卖方市场条件下，水电站优化调度模型的目标函数经常被描述为“发电量最大”“无益弃水量最小”或“发电耗水率最小”，其目的就是要使有限的水量尽可能转化成更多的电量，在耗水量最小的同时发电量最大。

国内外许多学者开展了这方面的研究。文献［1］基于研究汛期、枯期交易电量和电价之间的量价关系规律与关系曲线建立了以发电效益最大为目标的数学模型，并在模型中考虑了优先电量、集中撮合交易电量和外送电量。文献［2］基于独立储能在调频辅助服务市场上的收益优势，提出了包含独立储能的市场出清模型，分析了独立储能参与市场的效益、储能行为及收益，并将该模型方法扩展至包含备用辅助服务市场的场景。文献［3］研究了水电系统短期和长期的竞价调度问题，构建了大规模混合整数线性规划的模型，计算分析得出水电站侧竞价曲线，实现了短期和长期发电计划的联合优化。文献［4］在由32 台不同类型、非线性发电特性的水力发电机组组成的大型、复杂水力发电系统上，考虑了机组发电期间净水头变化对功率输出的影响及发电机组的非线性发电函数，基于成本最低目标函数提出了一种优化水力机组组合方法。文献［5］考虑了基于省域内电网供需平衡，结合区域控制性能评价指标，综合考虑网内新能源电源、同步发电机发电计划、负荷需求等因素，得到合理的省域电网内总体AGC 调频容量需求，提高了电网侧辅助市场的经济性。

目前关于电量和辅助服务市场的研究多单独从电网侧或电站侧角度出发，面对复杂、多元的电力市场环境，水力发电企业如何更加灵活地协调各台机组的出力，在提供电能和辅助调频服务的电力市场竞争中获得更大优势，赢得更多利润，是目前亟待解决的问题。本文在电力市场环境下结合电网侧与水电站的需求，综合考虑水库运行优化调度、电能与调频辅助市场三个方面，以某大型水电站实测数据为基础进行算例分析，提出以收益最大为目标函数的水电厂站优化调度运行数学模型，根据该数学模型提出水电厂站优化调度运行决策流程，在保障水轮机组工作在最佳运行区的前提下，使得电站工作在安全性最优、效益最优的环境下，最大化水电站在电力市场环境下的收益。

二、水电站优化调度运行数学模型

在电力市场环境下，水电厂站提供电能交易商品与调频辅助服务，受发电机组自身运行特性影响，电能与调频辅助服务存在耦合性［6］，发电量最大不代表收益最大。因此，应将电力市场环境下的市场需求纳入水电厂优化调度运行的研究范围内，不能忽视市场电价、营收效益等经济因素所发挥的市场作用。在此背景下，本文构建考虑基于电能与调频辅助服务耦合特性的以收益最大为目标函数的水电厂站优化调度运行数学模型。

（一）问题描述

考虑水电站电能收益与在辅助服务市场上获得的收益，给定发电功率报价、调频辅助服务市场出清价、全厂耗水量与机组耗水量，综合考虑常规水力电力调度约束条件，通过控制机组出力与规划水电站开停机数量，使水电站在调度期内综合收益最大。

（二）目标函数

式（1）中，S为全厂发电总收益（即收益运行计划下的全厂收益）（元）；Ni为i时段的全厂总出力（MW）；Ci，Creg，i分别为i时段的发电功率报价（元/MW·h）和i时段的调频辅助服务市场出清价（元/MW）；T为调度内时段数（h）；Mt为i时段内小时数，若T＝96，则Mt＝0.25h；Q为全厂总耗水量（m3/MW）；Qk（Nk，H）为第k台机组在出力Nk与水头H时的耗水量（m3/MW）；n为机组台数。

式（1）中Qk（Nk，H）、Ni、Nk计算函数如下：

式（2）中，a2、a1、a0分别为第k台机组的出力-耗水量特性参数，用最小二乘法，在某水头下机组出力与相应耗水量的对比关系数据绘制二次多项式曲线Qk（Nk，H）得到。a2、a1、a0即为该多项式的系数；Nk为第k台机组的出力（MW）；Hi为i时段的水头（m）；qi为i时段的引用流量（m3/s）；i第k台机组的效率。

（三）约束条件

1.水量平衡约束：

2.库水位约束：

式（4）中，Zm，t为电站在第t时段内，满足规定范围的最低水位，一般为死水位或综合利用要求的最低水位；为电站在第t时段满足规定范围的最高水位或水位上限，在非汛期时取值通常为正常高水位，汛期则取汛限水位，单位均取m。

3.库容约束：

式（5）中，为电站在第t时段内满足规定范围的最小库容，一般为死库容或综合利用要求的最小库容；为电站在第t时段满足规定范围的库容上限，通常非汛期取正常高水位库容，汛期取汛限库容，单位均取m3。

4.发电流量约束：

式（6）中，为电站在第t时段满足规定范围的最小发电流量，以保证机组正常出力；为电站站在第t时段满足规定范围的最大发电流量，单位均取m/s。

5.出库流量约束：

式（7）中，为电站在第t时段满足规定范围的最小出库流量，以保证机组正常出力；为电站在第t时段满足规定范围的最大允许出库流量，单位均取m3/s。

6.出力平衡约束：

式（8）中，Nt为t时段内的全厂总负荷，等于t时段内水电站内所有开机机组出力的总和，MW；Nt，k为当前t时段内第k台机组所带负荷值大小，MW；rk代表第k台机组的运行状态，当第k台机组处于发电运行状态时rk取1，当第k台机组处于停机状态时rk取0。

7.出力约束：

式（9）中，Nt，kmin、Nt，kmax分别为t时段内第k台机组负荷的下限值和上限值，也可称为出力的最大值和最小值，单位均取MW。

8.水头约束：

式（10）中，Hmin、Hmax分别为水电站的最低、最高允许水头（m）；Hup、Hdown分别为上、下游水位（m）。

9.调频约束：

式（11）中，Nplan，i为第i个点的96 点计划出力曲线取值，i=1，2，……，96。

10.非负约束：以上所提变量均为大于零的正数。

三、电力市场环境下水电站优化调度运行决策流程

水电站收益包含发电功率收益与参与辅助服务市场调峰调频获得的收益，以水电站收益最大为目标函数的数学模型优化运行流程，应考虑水量约束、出力约束等约束条件控制机组出力与规划水电站运行机组数量，使机组工作在最优工作区间的同时耗水量最小。综合优化水电站运行模式、提升收益率的考虑，本文提出了一种基于电力市场环境下水电站优化调度运行决策流程，如图1 所示。

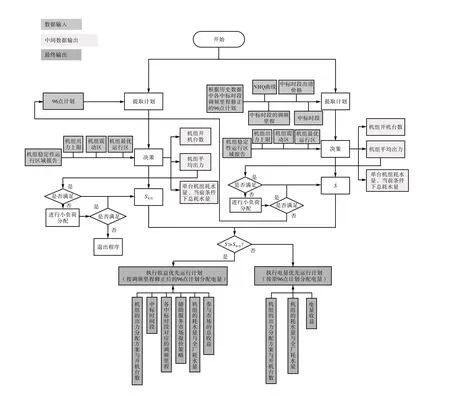
图1 电力市场环境下水电站优化调度运行决策流程

根据前一日调度下发的日负荷计划将24 个小时分为96 个时段（即96 点计划），首先在提取计划中同时输入的电厂原96 点计划曲线与根据历史调频辅助服务市场数据修正的96 点数据，根据机组出力上下限、机组震动区、机组最优工作区等机组稳定性运行区域作为限制条件，以约束在当前总出力条件下工作机组台数；根据全厂总负荷、工作机组台数，优先按照平均原则分配各台工作机组所承担的负荷，保障工作机组在最优运行工况内。其次继续考察平均分配的负荷是否满足机组最优运行条件，如果满足则计算此时的纯电量收益S有功（即电量优先运行计划下的全厂收益），或式（1）所示的参与调频辅助市场情况下的总收益S，如不满足机组最优运行工况，则进行小负荷分配。小负荷分配是指将一台工作机组的总负荷分配到两台工作机组上，继续考察这两台机组的运行工况是否满足机组运行条件，如果满足则计算纯电量收益S有功或S，如不满足则退出流程或返回原96 点计划输入重新计算。如果此时电站内的所有机组均已开机，在原96点计划输入情况下，则直接退出流程；在修正96点计划输入情况下，则返回原96 点计划输入，重新计算开机数量、各机组承担负荷。最后比较S有功与S的大小，如果S＞S有功，则执行收益优先运行计划，对应输出机组的出力分配方案与开机台数、中标时间段、参与市场的总收益等结果数据；如果S＜S有功，则执行电量优先运行计划，输出开机台数与机组负荷分配方案、耗水量、电量收益等结果数据。两种计划最终得到的结果数据均可作用于指导运行值班人员制订N+1 日机组开停机计划，运行人员可进行最终审核并择优执行最终计划。

四、算例分析

为了验证本文所提方法的有效性，采用总装机容量4900MW 的某大型水电站一段时间内的实测数据作为算例进行分析研究，该大型水电站共安装7 台单机额定容量为700MW 的水轮发电机组。

水电站优化调度运行是一组集合了多种组合优化的课题，具有强约束、非线性、多目标、多约束等特点，常规线性计算方法难以较快求得最优解。作为一种优化算法，遗传算法有较长的发展历史，在各项优化算法中发展成熟且稳定，因其搜索能力快、比较能力强、过程简单等优点在求解复杂组合优化问题中具有明显优势。本文使用遗传算法作为目标函数的求解方法，根据96点计划，每个时段设置一个全厂总出力，根据水头、机组稳定性运行区域和调频裕度等实际情况约束，使每台机组的出力不大于当日调度下发的单机最大出力。

输入数据后经决策流程可得如图2―图4 所示的结果。由于加上电量收益后结果趋势不明显，故本文在结果分析部分去掉电量固定收益，只保留电厂在调频辅助服务市场上的收益结果，如图2所示，可以看出，随着遗传算法迭代次数的增多，电厂在辅助服务市场上的收益越多；此时全厂的24 小时耗水量如图3 所示，可以看出，与计划值对比，由于参与调频辅助市场，耗水量曲线呈波动状态；24 小时的全厂出力情况图4 所示，可以看出，由于参与调频辅助市场，根据水轮NHQ特性曲线，全厂总出力曲线与耗水量曲线波动趋势基本相同。

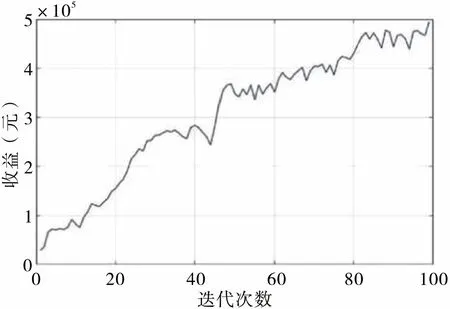
图2 电厂在调频辅助服务市场的收益

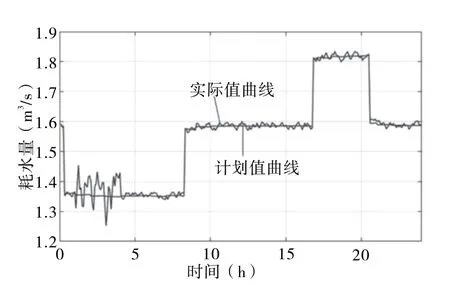
图3 全厂耗水量情况

图4 全厂总出力情况

五、结语

面对交易品种协同发展的电力市场环境，计划电力经济思维中“发电量最大=发电效益最大”的目标已无法满足当前环境下发电企业经营目标所需。由于水力、电力调度运行的多种约束因素，水电站的电量交易、调度运行与市场化交易存在耦合关系，本文综合考虑电力市场环境下水电站的安全生产与发展需求，提出了以电量收益与辅助服务市场收益之和最高的目标函数，兼顾运行调度、机组工况约束与水量约束等常规限制条件，基于收益最大目标函数提出了电力市场环境下水电站优化调度运行决策流程，分别讨论了不同情况下水电站调度运行的决策过程。最后，采用遗传算法对某大型水电站实测数据进行算例分析，结果表明，本文所提目标函数、决策流程可以有效提升水电站总收益，同时使机组工作在最优工况的同时耗水量最小。