结合QEM的布料层次化动态模拟方法
马晓彤, 祝双武, 王世豪, 李丑旦, 马阿辉
(西安工程大学 纺织科学与工程学院,西安 710048)
20世纪以来,对刚体、流体、布料及软体等可变形对象的模拟是计算机图形学领域的重要研究话题。与更为追求结果准确性的学科相比,基于物理的模拟领域主要关注的问题是稳定性、模拟速度及视觉上的合理效果。布料模拟主要应用于电影电视、计算机游戏、纺织服装设计等领域,模拟现实世界中布料在某一刻的运动形态,近几十年来宝贵的理论和技术方法层出不穷[1]。
关于布料物理模型的建立,离散体模型采用离散质点进行布料建模,通过质点之间的相互作用力来维持布料在运动时的形态,典型方法如质点—弹簧模型[2]、粒子模型[3];连续体模型将布料看作连续介质对其进行建模,典型方法如弹性变形模型、有限元方法[4]等。建立布料模型后,按照传统模拟流程需要对布料质点进行受力分析,根据牛顿力学公式计算质点的加速度,进而求出速度和位置。在时间积分法中,隐式欧拉积分[5]在求解时允许使用较大的时间步长对布料进行模拟并保证了系统的稳定性,但隐式积分涉及非线性方程的求解问题,计算较为复杂;Liu等[6]将非线性系统的求解转化为最优化问题,将原方程的求解等价于最优化问题目标函数的极值求解,Wang等[7]提出了一种使用雅可比预处理和切比雪夫加速的新梯度下降方法,提高收敛速度的同时降低了计算成本;Bouaziz等[8]在文献[6]的基础上提出了投影动力学,Müller等[9]提出了基于位置约束的动力学方法(PBD),使用几何约束的概念来代替布料模型内部的弹性力,在每个时刻只需要访问质点位置,降低了内存访问的频率和计算成本,减少了数据之间的相互依赖,在固体、流体、布料等形变体方面都有对应的模拟方法[10-11],因此PBD广泛应用于游戏、仿真等领域。
虽然PBD方法的计算过程较适合于实时模拟的场景,但其运行速度和布料整体模拟效果会受到网格分辨率及迭代计算次数的限制。当布料网格分辨率较低时,较少的迭代次数就可以使质点的位置快速矫正,运行速度较快,对于高分辨率网格而言运行效率则明显下降。为了提升PBD方法在高分辨率布料网格上的收敛速度,缓解其依赖约束求解顺序造成的收敛慢等问题,基于多重网格思想的层次化模拟方法[12]应运而生。多重网格是将原始精细网格逐步粗糙化,构建多层次、质点规模递减的网格序列,根据计算过程中的误差分量收敛特性,快速消除高频误差,将收敛较为缓慢的低频误差转移到粗网格中去消除,避免单层布料网格迭代次数的显著增加。
Müller[12]将多重网格方法引入到基于位置约束的模拟中(Hierarchical Position Based Dynamics,HPBD),从精细网格中挑选质点子集作为下一层较粗糙网格的点,将精细层网格中的位置预测值自顶向下传递,再由粗糙网格迭代计算后向上一层较精细网格延伸,提升了PBD方法的模拟速度。HPBD方法基于初始网格的信息在较粗糙网格上创建新约束,而没有直接在粗细网格之间进行约束的传递,Jeon等[13]提出了一种基于软约束的约束粗化方法并应用到隐式积分上,使得多重网格方法更好地应用于布料及服装模拟中;Xian等[14]提出了基于Galerkin多重网格法的仿真方法,采用最远点均匀采样法构建多重网格,使用分段常数权重由粗糙网格向较精细网格插值,可以使用不同的迭代计算方法及多重网格迭代模式;靳雁霞等[15]使用粒子群算法对布料表面进行搜索,优化了多精度布料的建模速度和精度;郑华等[16]对基于位置约束的层次化模拟进行了改进,使用决策函数法构建各层布料网格并提出一种关联模型来确定父子间的权值信息,其收敛速度可以使模拟效果较快地达到理想状态,具有一定的稳定性。这些文献皆对层次化布料模拟做出了贡献并各有侧重点,本文同样进行了层次化布料模拟方法的研究,采用基于二次误差度量的边折叠策略对布料几何多层网格进行构建,得到的层次网格模型可以维持稳定的约束效果。同时提出一种混合平滑方案,结合SOR法及GS法各自的优点来对布料系统进行迭代求解。由于质点受其周围相连拓扑结构的粒子信息影响,结合空间插值方法反距离加权(Inverse Distance Weighted,IDW)在层次网格间进行父子点权重信息的计算和矫正信息的传递,可以使待插值点获得较为平滑的结果。实验过程中采用布料自由落体后悬垂、与球体碰撞交互等方式进行了测试,均显示模拟效果良好。
1 模拟方法概述
1.1 多重网格方法
在PBD方法中,质点的目标位置在多个约束的求解过程中不断受到影响,如果过度增加迭代次数会导致模拟效率降低。对单层网格粗化后进行迭代也可以提高收敛速度,却会降低网格精度。因此,在模拟中使用层次化的网格结构,提高布料分辨率的同时还可以提升计算速度,是一种高效可行的模拟方法。
多重网格法(Multigrid,MG)广泛地应用于数值计算领域[17],核心思想是利用各粗细层次网格之间的连接关系来降低求解布料系统或其他问题时的计算量。在布料模拟过程中,较粗糙网格上的约束组成规模相对较小的方程组,采用Gauss-Seidel等迭代方法在层次网格之间进行计算。多重网格方法虽然增加了网格层数,并且需要为每一层网格单独建立约束,但因为迭代次数的减少,在达到同样的模拟效果时,总的计算量会少于单层网格,有效提高迭代算法的收敛速度,构建流程如图1所示。
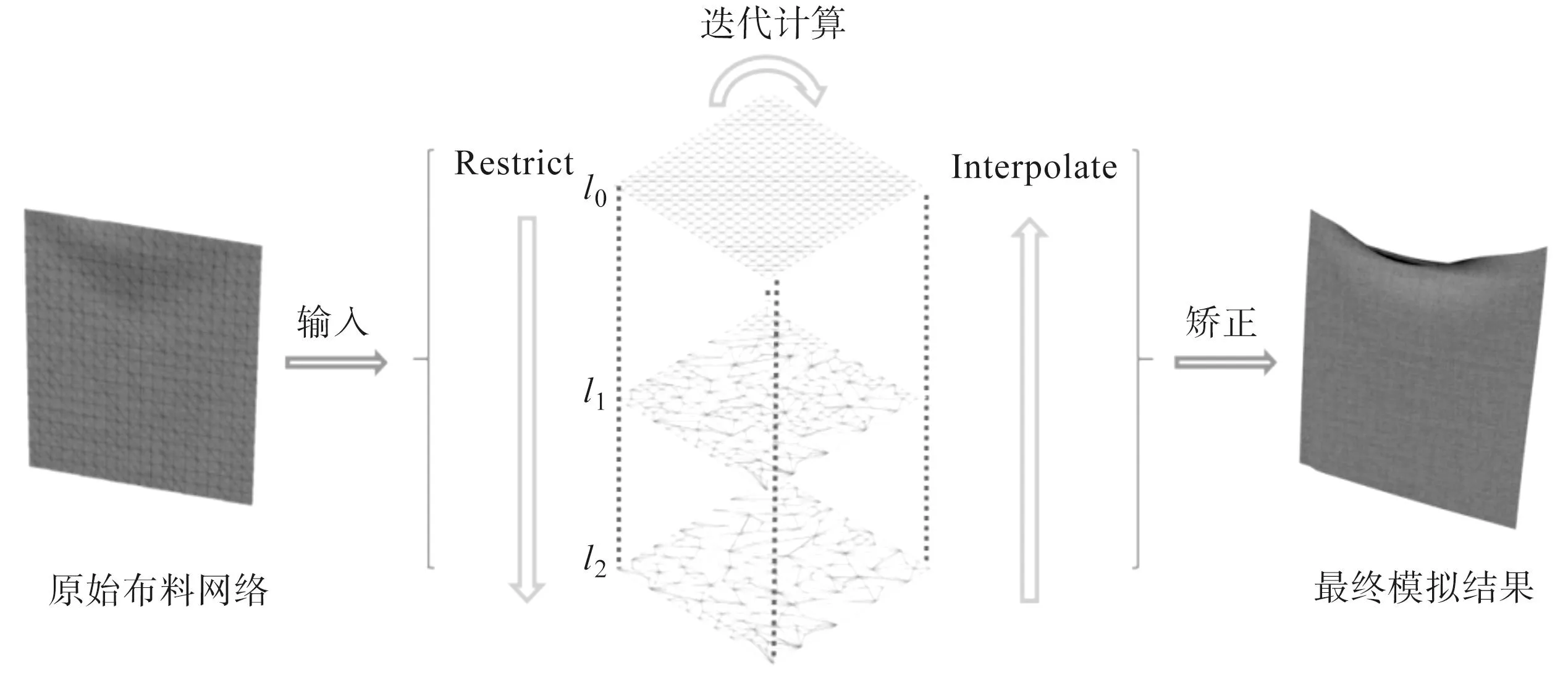
图1 布料多重网格结构
1.2 基于多重网格的层次化模拟
将多重网格方法应用到布料模拟过程后,将原始网格定义为最精细的一层,通过在上一层较精细网格中挑选质点子集来构造下一层较粗糙网格,在挑选时要保证当前网格的每个质点在它的质点子集中至少有两个连接点,避免出现质点丢失或重复的情况。将为下一层网格挑选出的质点标记为coarse,而fine则为要剔除的点,必须要保证质点子集内部的连通性,方便后续为其构建约束关系,还要在coarse点和fine点之间建立父子关系,用于传递矫正信息。文献[12]中以PBD原理为基础实现了层次化的位置动力学模拟,本文以质点的距离约束为例,位置矫正过程如下所述。
C(p1,p2)=|p1-p2|-d
(1)
式中:C(p1,p2)表示距离约束函数,p1、p2为进行距离调整的质点位置,|p1-p2|为两点间的实际距离,d为两点间的原长。
当函数等于0不成立时,需要找到位移修正量Δp对质点的预测位置进行矫正。此外,模拟在三维空间中进行,求解约束方程时可能产生多个解,需要添加另外的约束来指定Δp的方向。将Δp限制在约束的梯度方向来使系统最快稳定,保持系统的动量和角动量守恒,如下式所示。
Δp=λpC(p)
(2)
式中:标量λ为缩放系数,用于控制梯度方向上的变化幅度。
下一步对距离约束函数在点p1、p2处分别求梯度,如下式所示。
(3)
(4)
将式(3)(4)代入式(2)可求出距离约束中两点的修正量Δp1和Δp2,并将其施加到原位置即可完成矫正,如下式所示。
(5)
(6)
本文对文献[12]中方法进行了实践,布料进行悬垂、碰撞交互的模拟效果如图2所示。
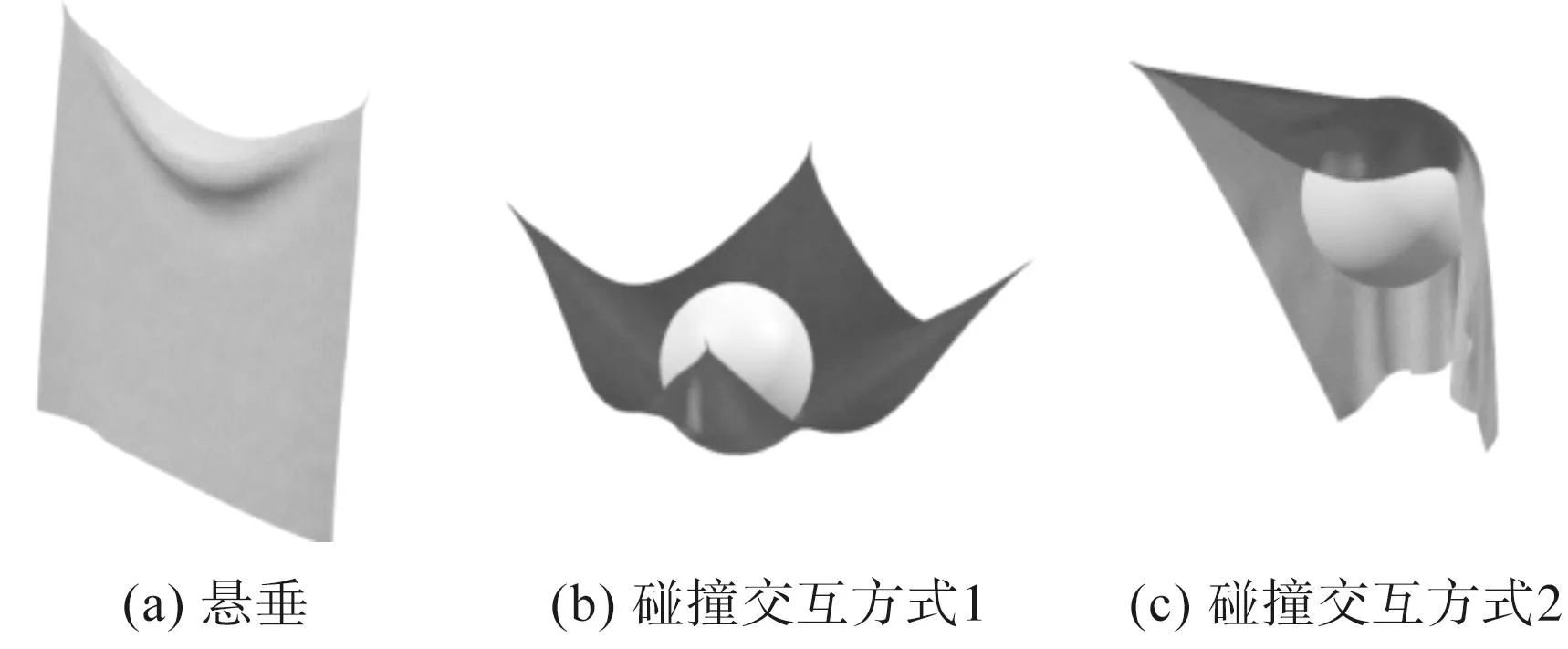
图2 层次化位置动力学模拟效果
采用多重网格进行布料模拟,具体流程如下:①基础网格模型的建立。完成初始网格质点及其约束信息的建立过程。②确定层次间网格质点的简化规则。进行多层网格的粗化过程,决定质点是否剔除及剔除的先后顺序,标记出coarse点及fine点。③进行层次网格的构建。建立每层网格的约束信息集合,保持网格连通,避免出现孤立点,删除多余的连接边。④进行层次间信息传递。构建好各层网格之后,建立层次之间的连接关系,用于原始数据和矫正信息的传递。⑤选择迭代方法对层次网格系统进行求解,然后对原始网格质点位置进行矫正。
2 基于二次误差度量策略的层次化方法
按照前文模拟流程,下一层网格质点的选择及层次网格构建是解决这个问题的核心步骤。本文使用文献[12]方法对布料进行模拟时发现,当网格层数逐渐增加,为网格简化所挑选出的质点数目是不均匀的,在后续层次之间传递矫正信息时也会影响到函数执行效率。同时构造出的网格会有不规则多边形的出现,无法保证网格的全局三角结构,对布料进行约束求解时,网格整体的约束效果和理论状态会产生区别,那么在最终模拟效果的表现上就会与单层网格收敛状态有一定的误差。
基于以上原因,构造高质量的布料网格是非常必要的。本文采用边折叠法,基于二次误差度量策略来构建多重网格,该方法在众多模型简化算法当中具有相对较高的计算速度和较小的内存消耗。将其引入到布料层次化模拟中,通过控制简化率来建立层次网格,可以在较短的时间内生成质量较好的三角网格,除简化布料规整模型外,也适合于三维服装模拟中层次网格的构建,较大程度地保留不规则模型的细节特征和质点分布情况。
2.1 层次网格的构建
边折叠方法[18]基于能量函数优化挑选网格中的边进行精简,将边折叠成一个顶点,并从网格中减去这条边相连的所有三角形,及时修改边折叠后周围的几何拓扑信息。可将其分为全边折叠与半边折叠,其中半边折叠的合并顶点位置是原边两个端点之一,简化后的网格模型中的顶点是原模型的子集,它可以更加快速地在层次网格之间传递矫正信息,相较于全边折叠只需要更少的存储空间,具有更高的网格构建速度。基于布料模拟实时性和高效率的要求,本文选择简化效率更高的半边折叠方法来完成粗细网格的建立。对边(v1,v2)进行简化,顶点v1合并到v2的位置,并对周边拓扑信息进行修改,如图3所示。

图3 半边折叠示例
在边折叠算法中有两个问题需要关注,边折叠的顺序和新合并顶点的位置。新顶点的位置根据半边折叠规则确定,边折叠的顺序则依据二次误差度量策略[19],进一步降低边折叠方法的时间复杂度,获得较优简化效果的同时提高计算效率。网格中每个顶点看作周围三角面所在平面的交集点,设plane(v)为点v关联的所有三角面集合,每个平面方程如下式所示。
ax+by+cz+d=0(a2+b2+c2=1)
(7)
式中:p=[abcd]T代表平面方程的系数。
每个三角网格所在平面拥有一个Kp,表示为基本误差矩阵,如下式所示。
(8)
网格中的每个顶点拥有一个4×4误差矩阵Q,对该顶点的所有Kp求和得到,如下式所示。
Q=∑p∈plane(v)Kp
(9)
将顶点的位置到它所有关联三角形面的距离平方和定义为折叠误差,首先初始化网格中所有点的误差矩阵Q和误差代价Δ(v)。统计所有参与折叠的边,在每条边(v1,v2)的两个端点中选择代价较小的点,选作新合并点v,后续将该边折叠到该点。Q1、Q2分别为原两端点的误差矩阵,对合并顶点v的位置进行更新后,其误差矩阵更新为Δ(v)=Q1+Q2,折叠误差可以通过二次项表达式Δ(v)=vTQv重新计算得出。根据计算出的误差代价对所有边进行排序,构建最小堆,依次折叠当前误差代价最小的边,删除所有的退化边和三角形,并更新受该边影响的其余边的折叠误差及新合并顶点v的位置,直到满足该层网格简化条件。
综合以上过程,本文将基于二次误差度量的网格简化和布料模拟流程进行了结合,对网格建立方案进行了分析和设计,构建流程如图4所示。
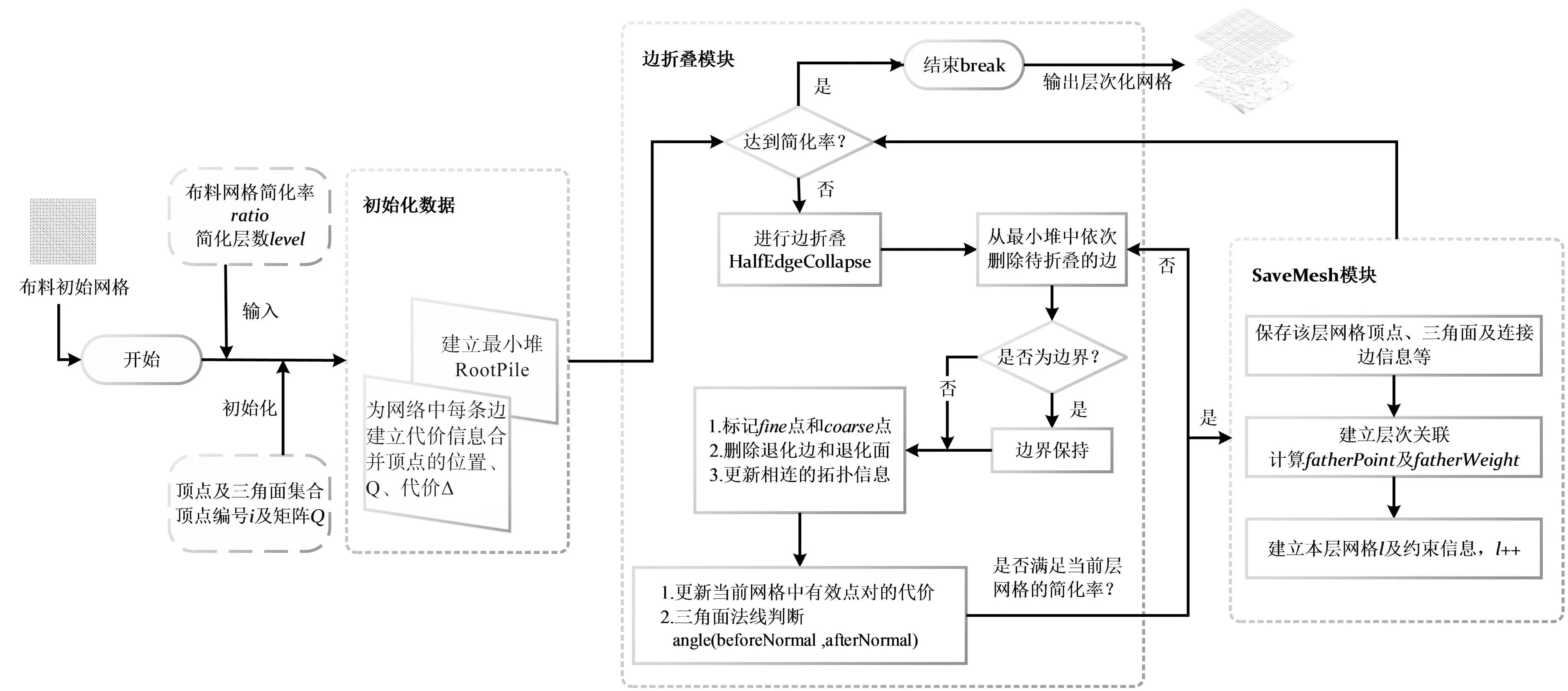
图4 层次化构建流程示意
在简化过程中要避免网格重叠的问题,对边折叠前后三角所在平面的法向量进行计算,通过点积计算两个向量的夹角并判断当前两个向量的朝向。如果折叠前后的法向量点乘小于0,即两向量夹角大于90°,则折叠该边后出现了网格重叠,呈现不合理的布料网格拓扑,会产生错误的计算结果进而影响模拟效果,需要进行法线翻转对网格结构进行调整。
同时,注意不是所有的边都满足折叠条件,为了维持布料网格形状,在折叠时要进行边界判断。如果包含该边的三角面只有一个,则当前选中的待折叠边是网格边界,要进行边界保持,将位于布料网格边界的质点定义为保持点,保持点不可以折叠到布料网格内部。图5(a)(b)分别为网格折叠和未进行边界保持的错误构建效果,图5(c)(d)中则是布料悬挂状态下正确结果和错误结果的对比。

图5 错误简化效果示例
通过以上分析,层次质点的选择和层次网格的重建在边折叠的过程中完成,采用以上方法进行三层布料网格构建的实验效果如图6所示。
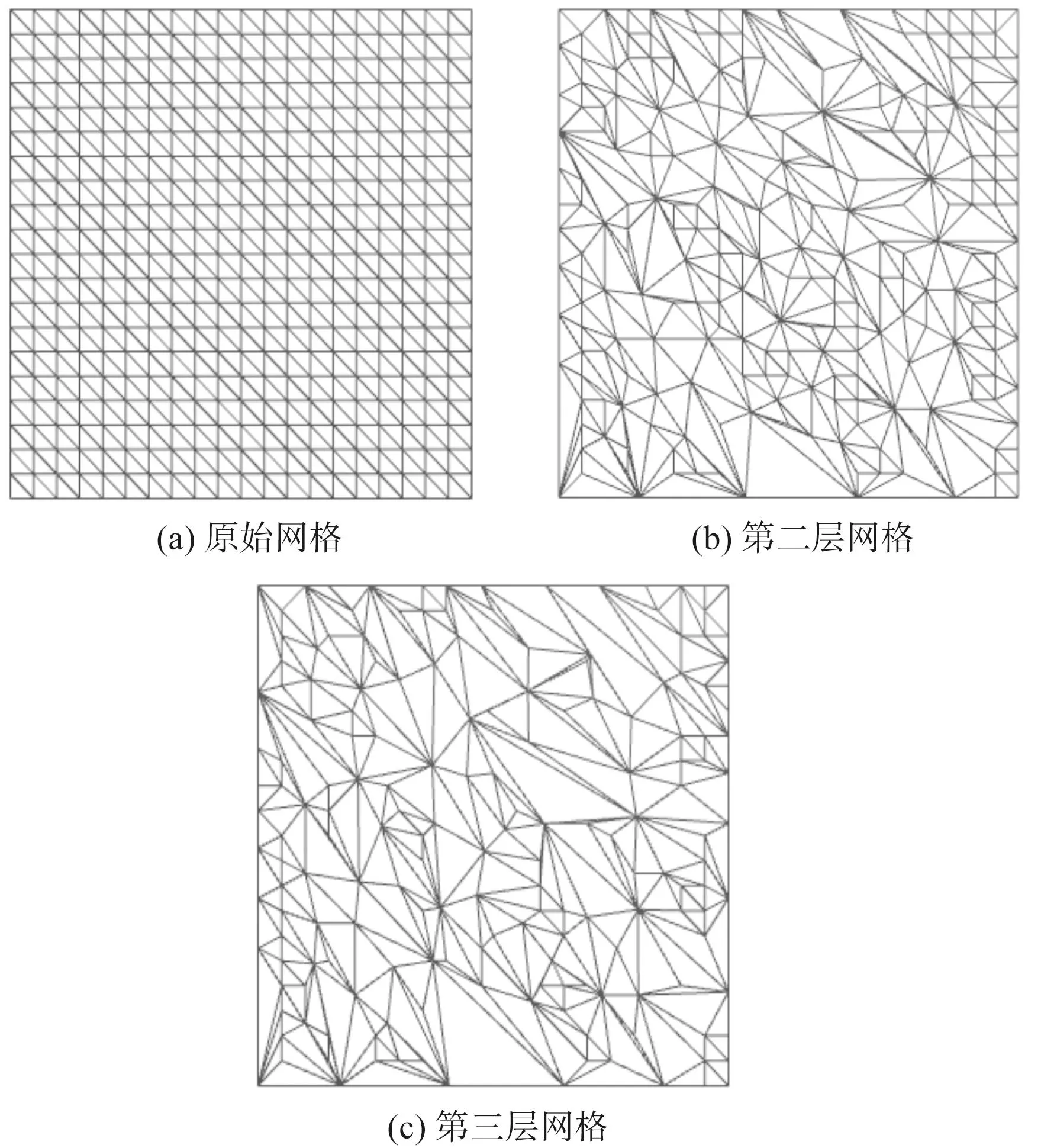
图6 基于QEM方法构建三层网格
2.2 层次网格的关联
构建好布料多层网格后进行层次网格之间数据信息的传递,将与fine点相连的所有coarse点视为其父节点,此时需要确定fine点与其父节点之间的权重信息,并根据权重及父节点位置来更新fine点,如图7所示。
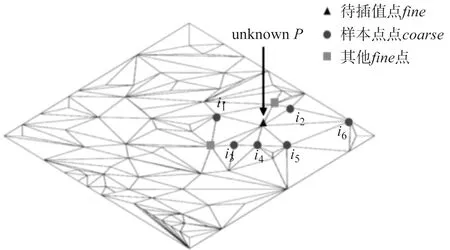
图7 质点分布示例
本文借鉴了反距离加权法的思想进行插值,它常用作大规模地形模型中数据的处理,假设网格中每个已知数据输入点对周围其余顶点都有局部的影响,且与距离相关。
本文以图7为例,将当前层布料网格中的coarse点视为样本点,而fine点为待插值点。以样本点与待插值点间的距离为权重进行加权平均,距离待插值点越近的样本点分配的权重越大,即权重随距离的增大而减小。首先计算待插值点到所有影响它的样本点的距离di(i=1,2,…,n),随后计算每个样本点的权重wi,如下式所示。
(10)
式中:p为幂值,样本点的权重与反距离的p次幂成正比,它决定了权重的下降速度。p值较大时,距离较远的样本点权重会迅速减小,待插值点更接近邻近样本点的值;p值较小时,网格质点数据更加平滑。
计算出权重后,根据下式对其位置进行加权计算,更新fine点位置。
(11)
3 混合平滑方式
3.1 平滑方法的选择
在几何多重网格的V-cycle过程中,预平滑首先用于改进模拟的初始值,旨在通过减小误差来降低后平滑所需的迭代次数。预平滑与后平滑常结合起来用于加速线性方程组的收敛,进一步降低网格中的残差,并增加迭代的稳定性。SOR迭代法是GS法的改进,在迭代计算的基础上引入一个松弛因子w,进行加权平均以求解方程组,松弛因子的取值会直接影响到算法的收敛性和速度,甚至可以使发散的迭代过程变得收敛。层次化模拟旨在改善网格分辨率增加后计算速度下降的问题,而SOR迭代法恰好适合在网格尺寸较大时使用,其简化计算公式如下式所示。
xk+1=xk+wrk(0 (12) 式中:xk+1和xk分别为第k+1次和第k次的迭代结果;rk为第k+1次迭代的修正量;w为松弛因子,其最合适的取值需要在计算过程中具体分析[20]。 相比于GS和Jacobi作为预、后平滑方案,SOR具有更好的局部平滑性和全局收敛性,能够更有效地消除数值误差。为了进一步验证SOR迭代的先进性,本文基于PBD方法,设置51×51的布料网格,在只添加距离约束的情况下测试了采用Jacobi、GS、SOR三种不同的方法时布料收敛效果,如图8所示。 图8 三种方法收敛速度对比 从图8可以看出,Jacobi法的收敛速度较慢。实验中设置w=1.9,SOR法的相对误差在耗时1 671 ms与3 300 ms时,分别下降到10-2与10-3,相较于GS法其收敛速度提升了15.7%和25%。基于SOR方法的优点及实验结果对比,本文提出混合平滑方式,将SOR方法作为前平滑,GS方法作为后平滑方案。在V-cycle的向下冲程中,SOR法通过调整松弛因子可以更快地平滑误差并将其限制到较粗层次,而向上冲程中需要从较粗网格计算出较细网格上的解,使用GS法可以简化其实现步骤。 本文实验在主频为3.30 GHz的Intel(R)Core(TM)i7处理器和16 GB RAM内存的Win 10操作系统设备上进行,使用Unity3D引擎进行渲染。首先对布料层次化模拟结果进行实验,设置同样的网格质点数目,分别迭代计算3、5、9、27次,多重网格层数为3,重力采用-9.8 N等条件,分别采用了PBD方法、文献[12]方法及本文方法,布料进行自由落体运动后悬垂效果如表1所示。 表1 模拟效果对比 从表1中PBD方法可以看出,质点数目在千级别时,层次化方法迭代10次以内就可以获得较好的模拟效果,而该方法整体表现出的拉伸性较强,布料局部位置没有较好地收敛,增加迭代次数至27次时才达到后两种层次化方法计算9次时的效果,且模拟速率相对较低。表1中本文方法则展现了较为出色的模拟结果,特别是在布料质点位置的快速有效收敛方面表现优异。可以看出,本文方法建立了较高质量的拓扑网格,如表1中小方框所标注,与前两种方法相比,在拉伸点处等关键位置对质点位置进行了更精确的约束处理,能够较好地模拟布料在拉伸情况下的形变行为。 为了验证本文方法在分层模拟方面的有效性,在实验中与常见的布料模拟方法进行了对比研究。具体而言,首先为网格设置相同的质点数目并固定迭代次数及GS平滑方法,让布料模型从静止开始运动;其次分别使用了隐式积分法、PBD、文献[12]及本文方法对布料收敛速度及形变结果进行了对比。如图9(a)所示,只设置距离约束的条件下,由于约束数量较少所以分层模拟的优势并不明显,当误差下降到10-3时拉开差距;在图9(b)中,同时设置了距离约束和弯曲约束,可以看出多重网格方法开始发挥其优势,相对误差在10-2时,本文方法与PBD和文献[12]的方法相比收敛速度分别提升了26.5%和10.72%,误差下降到10-3时则分别提升了24%和15.7%,在模拟效果上也同样表现优异。 图9 三种不同方法收敛速度对比 在前文的QEM层次化模拟的条件下,采用本文混合方案时布料系统的收敛性,如图10所示。同样X轴表示模拟耗时,Y轴表示每次平滑前后迭代中测量的相对残差,松弛因子w=1.1。V(SOR,GS)表示SOR用于预平滑、GS用于后平滑的情况,结果表明,V(SOR,GS)相较于其他两种混合平滑方案具有更快的收敛速度,得以更迅速地消除误差。 图10 平滑方案对比 通过分析实验结果并结合一些经验规则和启发式方法,发现本文所建立的层次网格中收敛速度与网格间质点数目的差异密切相关。若较粗网格中质点数是其上层细网格的1/2及以上时,可以较大程度地减小误差,若网格间数目差异过于大时则可能会引发布料系统的不稳定问题,因此在选择预平滑和后平滑方案时需要根据所求解系统的特点进行调整。 在关注速度的同时,为了验证本文提出的层次网格构建方法及所采用的混合平滑方式可以模拟出稳定可靠的效果,在基础模拟效果上添加了风力作用及小球碰撞,观察其在外力作用下的表现,并从模拟结果中随机选择某一帧作为代表性样本进行分析。如图11所示,在风力作用下布料产生了自然的波动,与小球碰撞时未出现任何穿透和不稳定现象,因此表明本文方法在处理重力及拉力、风力等外部作用时均可保持模拟效果的稳定性。 图11 布料模拟效果 针对传统基于位置的动力学模拟在布料网格精度提升时模拟速率会大幅降低,层次化位置动力学方法中随着网格层数的增加,网格质量不高、布料收敛状态不稳定等问题,本文采用基于二次误差度量策略的边折叠方法进行布料多重网格的构建,结合反距离加权法的思想进行层与层之间的数据传递及位置矫正,可以生成质量较好的布料三角网格模型,避免网格整体的约束结果出现较大的误差,同时采用提出的混合平滑方案进行误差的迭代。经实验验证,本文方法有效提高了布料模拟的收敛速度,单帧模拟耗时远小于单层网格方法,稳定性在测试中表现良好,提升了布料模拟的质量和效率。 《丝绸》官网下载 中国知网下载3.2 不同方法的对比分析

4 模拟实验效果及对比



5 结 语



