一类扰动脉冲时滞神经网络系统的指数反同步
陈润龙,关开中
(五邑大学 数学与计算科学学院,广东 江门 529020)
在过去的几十年中,人们提出并研究了包括滞后同步[1]、相位同步[2]和指数同步[3]在内的各种同步问题.然而,在现实生活中,还存在另一类现象,即反同步[4].它指的是驱动系统与响应系统具有幅度相同但方向相反的状态向量,因此当反同步现象发生时,两系统的信号之和趋近于零.反同步因在通信系统和激光应用等领域中发挥着重要作用而引起了研究者的关注[4-6].
时滞常存在于信号处理和网络传输等工程中[7-8].在信号处理系统、计算机网络等的优化控制中,系统的状态由于瞬时扰动而在某些时刻发生突变,即产生脉冲效应[5,9].从所产生效果看,脉冲可分为扰动脉冲和控制脉冲两类[10-11].如果一个系统本身是稳定的,在一定的脉冲作用下仍然能保持稳定,则此类问题称为脉冲扰动问题,相对应的脉冲称为扰动脉冲[11].一个不稳定或稳定的系统,在一定的脉冲作用下可变为一致稳定、一致渐近稳定甚至指数隐定,则称此类问题为脉冲控制问题,相对应的脉冲为控制脉冲[11].特别值得一提的是,在很多实际系统中,脉冲和时滞是同时存在的.近年来,对同时具有时滞和脉冲系统的同步研究取得了较丰富的成果[7-8],对具有时滞或脉冲系统的反同步研究也取得了一定的进展[6],但对于同时具有脉冲和时滞系统的反同步研究则比较少.文献[5]研究了在脉冲作用下时滞混沌神经网络的全局指数反同步问题,建立了驱动-响应时滞神经网络系统指数反同步的充分条件,但文中所考虑的脉冲是控制脉冲.受文献[5,7-8]的启发,本文通过构造Lyapunov 泛函,将研究在扰动脉冲下具有常时滞的神经网络的全局指数反同步问题.
1 模型与预备知识
考虑以下具有常时滞的神经网络系统[8]:
为研究反同步问题,把系统(1)作为驱动系统,并构造如下具有脉冲的响应系统:
注1根据条件1,可以得到以下结论:
这表明,系统(3)在初始条件e(s)=ϕ(s)=0时,存在零解e(t)=0.
注2根据式(4),容易得到:
定义2[5]若系统(3)的零解是全局指数稳定的,则称驱动系统(1)和响应系统(2)是全局指数反同步的.
2 主要结果
定理1假设条件1 成立.若存在正定矩阵P,常数α>0,λ>0和βk≥1(k∈N),使得
成立,则驱动系统(1)和响应系统(2)是全局指数反同步的.
证明对于方程(3),构造Lyapunov 泛函:
根据式(5)以及不等式:2xTy≤ηxTx+η-1yTy,其中η>0,x,y∈Rn,有:
由式(9~12)得到:
根据式(8)和(13),有:
对任意的t∈(tk-1,tk],对式(14)从tk-1到t积分得到:
当t=tk,k∈N,根据式(6)以及不等式:λmin(P-1Q)xTPx≤xTQx≤λmax(P-1Q)xTPx,其中P为n阶正定矩阵,Q为n阶对称矩阵,x∈Rn,有:
根据数学归纳法,不难证明:
其中β0=1.由式(7)和(17)可得:
另一方面,根据所构造的Vi(t)(i=1,2),容易看出:
因此,由式(18~20)可以得到:
根据定义1,系统(3)的零解是全局指数稳定的,其指数收敛阶为这样,由定义2 可知,驱动系统(1)和响应系统(2)是全局指数反同步的.定理证毕.
注3从不等式(6)可以看出,定理1 是从脉冲扰动的角度提出的.这为我们提供了在一定扰动脉冲扰动下,系统仍能保持指数反同步的条件.特别地,当去掉驱动系统(2)中的脉冲,即Ik=0时,仿照定理1 的证明方法可以建立推论1.
推论1若存在一个常数λ>0使式(8)成立,那么驱动系统(1)和响应系统(2)在无脉冲情况下(即Ik=0)是全局指数反同步的.
3 数值算例
例考虑以下具有常时滞的驱动-响应神经网络系统:
驱动系统(21)和响应系统(22)之间的误差系统为:
这表明不等式(8)成立.
若在式(22)中没有脉冲作用,即Ik=0,根据推论1可以知道驱动系统(21)和响应系统(22)是反同步的,其状态如图1所示.
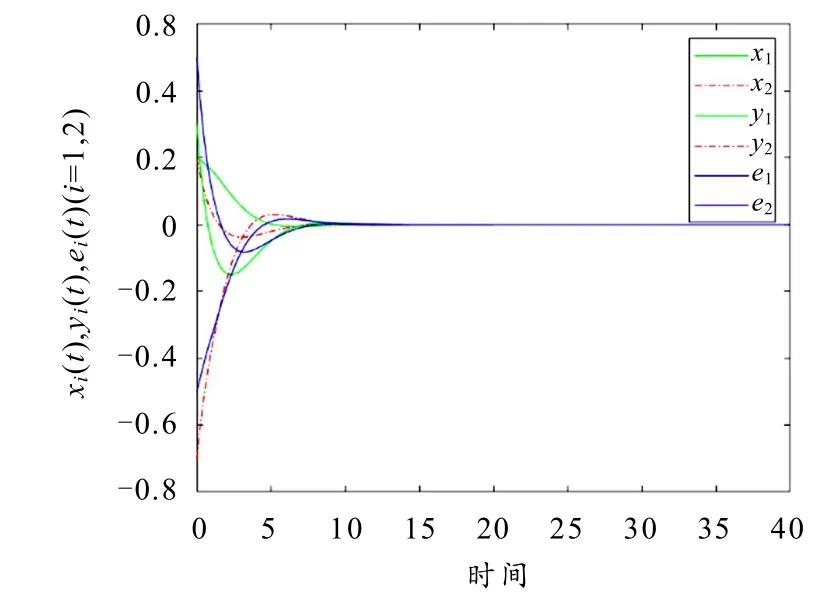
图1 系统(21)和系统(22)在无脉冲情况下的状态轨迹
设计一个脉冲方案(tk,Ik)k∈N来保持系统的反同步.选取脉冲矩阵Ik=diag {0.13,0.13},βk=1.28,tk=0.5,k∈N 可以验证:
因此,满足定理1的所有条件.这表明系统(23)是全局指数稳定,即驱动系统(21)和响应系统(22)是全局指数反同步的.反同步误差e1(t),e2(t)的数值模拟如图2所示.

图2 误差系统(23)在 Ik=diag {0.13,0.13}的状态轨迹

