基于预测需求量的物流仓储中心选址研究

程元栋,汪建伟,韩佰庆

(安徽理工大学 经济与管理学院,安徽 淮南 232001)

中共中央及国务院在2019年12月印发的《长江三角洲区域一体化发展规划纲要》指出,长江三角洲(以下简称长三角)地区是我国经济发展最活跃、开放程度最高、创新能力最强的区域之一,在国家现代化建设大局和全方位开放格局中具有举足轻重的战略地位。而物流业是经济发展的润滑剂,是区域经济发展的重要保障。其中,物流仓储中心作为重要的物流节点,其合理的选址可以减少运输时间,对于提高物流效率有着重要的作用。如何合理地选择长三角地区的物流仓储中心对于该地区经济发展有重要的意义。

对于仓储中心选址问题相关学者给出了众多研究方法。徐利民等[1]考虑了时间因素对企业仓储中心选址的影响,提出了动态选址方法,使得仓储中心选址更加灵活且能够符合实际需求,但是并未给出求解模型。丁小冬等[2]运用0-1混合整数规划法构建选址模型,将多种约束条件作为权重构建至模型中,使得整体物流费用最小。刘丹等[3]采用向量空间模型(vector space model,VSM)将影响仓储中心的多种经济性、环境性、社会性指标转化为向量空间进行分析。程旭[4]提出利用粒子群算法对仓储中心进行静动态分析,为仓储中心选址提供多种分析。苗将等[5]用优化的帝王蝶算法对京津冀地区进行逆向选址分析,精确求解出物流成本最低的仓储中心坐标。Maria等[6]对仓储中心动态选址问题进行详细的阐述,对不同的动态选址进行分类,并将不同的动态选址模型进行分析总结。Agzaf[7]考虑在多周期需求增加的情况下的设施选址问题,设计求址模型并利用算法求解,保证求解的设施能在客户可接受的时间范围将货物分配到位,对仓储中心选址问题求解具有启发作用。以上学者给出了求解仓储中心的多种思路和方法,对于求解仓储中心选址问题都有一定效果,但他们更加关注求解方法和模型,对于需求点的具体需求数据考虑不深,不是以自拟需求量就是以往年的需求量作为依据来进行仓储中心选址。这样会导致其仿真实验求解出的结果满足不了实际的要求,从而影响整个区域物流体系的效率,进而影响区域经济的发展,因此在进行仓储中心选址时应充分考虑需求点未来几年的需求量并以此作为仓储中心选址的依据。

对于物流需求量的预测有许多方法,其中指数平滑法就是一种比较常见的预测方法。米翠兰[8]认为二次指数平滑法实质是对历史数据进行加权平均并将其作为未来时刻的预测结果,对于中长期预测有较好的效果,她使用二次指数平滑法成功预测出某煤矿工人尘肺病患病率;赵婉[9]以货运量、货物周转量为指标,运用二次指数平滑法成功预测陕西省高速公路服务区物流需求量;李玉峰等[10]运用二次指数平滑法、径向基函数神经网络模型、多元线性回归模型等分别对水产品冷链物流需求量进行预测,通过与实际值对比及误差分析发现,使用二次指数平滑法预测的水产品冷链物流需求量与实际值拟合程度较好且误差较小。以上学者都证实了二次指数平滑法对于预测物流需求量有较好的效果。

为了解决目前仓储中心选址问题中对于需求量考虑不足及选址模型脱离实际、考虑因素较少等问题。利用二次指数平滑法求解出长三角地区未来3年的实际需求量,并基于该地区物流实际发展情况,构建考虑多种因素的求址模型。利用K-means聚类算法和遗传算法精确求解出满足总成本最低和物流效率最高的长三角地区物流仓储中心,从而提高该地区整体物流水平,为该地区经济发展提供有效助力。

1 预测需求量

1.1 指数平滑法

指数平滑法通过将观察值与实际值进行比较,来确保预测结果的准确性。这种方法基于布朗的理论,可以有效地捕捉时间序列的变化趋势,从而获得更准确的预测结果。论文利用指数平滑法来估算时间序列的变化趋势,并结合特定的预测模型来预测其未来发展趋势。

1.2 预测模型计算步骤

1) 时间序列的一次指数平滑值为

(1)

(2)

2) 建立二次指数平滑预测模型如下:

Yt+T=at+btT,

(3)

式(3)中,Yt+T为t+T期的预测值,单位为元;T为从t期向后推移的期数,单位为期。其中,

(4)

(5)

应用二次指数平滑法对物流量进行预测,其初始值及平滑系数∂的选择很关键。大多数研究人员建议在数据集项数较多时(一般大于20个),使用第1期的观测值或之前的观测值进行指数平滑是比较合适的。这样做不会太大地改变最终的结果,也不会太大地降低预期的准确性。因此,在进行数学模型分析之前,应该从初始观测值中挑选出几项并以其平均值作为模型的基准,从而使模型的准确性得到提升。此外,随着项数的增加,模型的平滑系数也将变得越来越重要。王慈光[11]认为当平滑系数较小且时间序列的项数较大时可以说明历史数据比近期数据起更大的作用。

因此,选取长三角地区27个中心城市2009-2022年的货物运输量数据,采用指数平滑法对中心城市2023-2025年的货物运输量进行预测。以2009-2011年的数据作为指数平滑初始值。通过Excel软件选取多个平滑系数进行实验,分析各城市2023-2025年预测值总平均相对误差,得出结果如表1所示。

表1 平滑系数对比Tab.1 Smoothing coefficient comparison

由表1可知,当平滑系数选取0.8时未来3年总的平均相对误差最小。说明当平滑系数较大时,近期数据对于预测未来的数据起更大作用,可以使得预测结果更贴近实际。因此,选取0.8作为平滑系数进行预测分析。通过Excel软件利用二次指数平滑法对各城市进行货运量预测,其中对合肥市的货运量预测实验结果如表2所示。

表2 二次指数平滑模型计算结果Tab.2 Calculation results of quadratic exponential smoothing model

由表2可知,从2011-2022年通过二次指数平滑法预测出的货运量与真实值误差基本都在5.00%以下,这表明二次指数平滑法对于预测货运量有较好的效果,可用于预测合肥市2023-2025年的货运量。通过实验发现其他城市的预测值相对误差也都维持在较低水平,因此可以证明二次指数平滑法在预测长三角地区中心城市货运量上的准确性。

2 物流仓储中心选址模型

2.1 模型假设

1) 各个备选仓储中心和各个区域需求点均可相互到达;

2) 各个备选仓储中心和各个区域需求点的距离采用欧氏距离计算;

3) 不考虑备选仓储中心到需求点需要多少辆车,假设运输工具充足;

4) 备选仓储中心坐标已知,各个备选中心的建设成本、运营成本已知;

5) 各区域需求点坐标和未来3年预计需求量已知;

6) 各个备选仓储中心到各个区域需求点的单位运输成本固定且已知;

7) 各个备选仓储中心到各个区域需求点的运输速度一致。

2.2 物流仓储中心选址模型

1) 仓储中心建设成本:

(6)

式(6)中,m为仓储中心数量,单位为个;Qi为仓储中心i的建设成本,单位为元;xi为0-1变量,xi为1时表示备选仓储中心i被选中,否则xi为0;S1为仓储中心建设成本,单位为元。

2) 仓储中心运营成本:

(7)

式(7)中,β为仓储中心i3年的运营成本和建设成本的比例系数;S2为仓储中心运营成本,单位为元。

3) 运输成本:

(8)

式(8)中,C为仓储中心到需求点的单位运输成本,单位为元;Sij为仓储中心i到需求点j的运输量,单位为t;dij为仓储中心i到需求点j的距离,单位为km;yij为仓储中心i提供给需求点j的需求量,如果没有需求量则yij为0;S3为运输成本,单位为元。

4) 总成本:

min(S)=S1+S2+S3,

(9)

式(9)中,S为总成本,单位为元。

约束条件为

(10)

式(10)中,J为各区域需求点集合:J={1,2,…,n}。

yij≤xi,∀i∈I,j∈J,

(11)

式(11)中,I为备选仓储中心集合:I={1,2,…,m}。

(12)

式(12)中,P为允许建设仓储中心的数量,单位为个。

tij=dij/V,

(13)

式(13)中,tij为备选仓储中心i到需求点j的运输时间,单位为h;V为仓储中心到需求点的运输速度,单位为km/h。

(tij+Ri)yij≤Tj,∀i∈I,j∈J,

(14)

式(14)中,Ri为备选仓储中心的响应时间,单位为h;Tj为需求点可接受的货物到达最长时间,单位为h。

式(10)表示每个需求点都需要1个仓储中心为其提供服务;式(11)表示当备选仓储中心被选中时才可以为需求点提供服务;式(12)表示仓储中心建设数量;式(13)表示仓储中心i到需求点j的运输时间;式(14)表示仓储中心的响应时间及运输时间之和小于需求点最长可接受时间。

3 K-means聚类算法

K-means算法是一种广泛应用的迭代式聚类算法。其步骤是:若要将数据分为K组,则随机选取K个对象作为初始的聚类中心,然后计算每个数据与各个聚类中心之间的距离,把每个数据分配给距离它最近的聚类中心。

K-means聚类算法中需要距离的计算,可以根据实际应用的特点和需要选择任意距离度量方法,如欧氏距离、曼哈顿距离等。不同的距离度量方式,只是在计算距离时使用相对应的距离计算公式,其余步骤不变。实验选择欧氏距离,采用误差平方和(sum of squared errors,SSE)作为质心位置的优化指标。因此,需要计算每个点的欧氏距离,也就是它们与质心的距离,并将误差平方和作为衡量标准。对于指定的K个簇,簇内点之间的距离越小,对应的SSE也越小,聚类的效果也越好。当SSE接近于0时,表明模型的选择和拟合效果更佳,从而使得实验结果更加准确可靠。

其中数据到簇质心的欧氏距离计算公式为

(15)

式(15)中,D(Xl,Cm)为2个目标之间的欧氏距离,Xl为第l个数据,Cm为第m个聚类中心。

SSE计算公式为

(16)

式(16)中,PSSE为误差平方和,x为簇内的目标,cl为簇质心。

4 遗传算法

遗传算法是从大自然生物进化规律抽象出来的随机全局搜索优化算法,它借鉴了达尔文生物进化论和孟德尔遗传学的原理,以更加精确的方式求解复杂的问题。遗传算法能够实现全局搜索,并在搜索过程中自主学习,不断适应环境得到最优解。利用计算机模拟技术,可以把原本用于研究问题的参考值转换成可用于描述特征集合的编码,并且根据适应性函数来衡量特征集合的表现,同时利用编码集合来构建个性集合,并且可以采用多种方法(如交叉、变异和迭代)来实现个性集合的持续发展,从而获得更加完善和有效的结果。遗传算法流程如图1所示。

图1 遗传算法流程Fig.1 Flow of genetic algorithm

由图1可知,算法依次进行参数初始化、初始化种群、选择个体交叉、变异子代、评估子代,然后形成新的种群,再判断种群是否满足收敛条件(收敛条件为成本最小),满足收敛条件则计算目标函数值,不满足则重复进行交叉变异操作,直到满足条件则结束算法输出结果。

5 仿真实验与分析

5.1 实验数据与环境

为了验证算法在求解长三角地区中心城市仓储中心选址问题时的有效性与正确性,建立了长三角地区中心城市数据集,如表3所示。以此数据集为选址算例,在具有Intel(R) Core(TM) i5-7200U处理器和Windows 10系统的计算机上使用Matlab软件进行仿真求解。

表3 长三角数据集Tab.3 Yangtze River Delta dataset

由表3可知,需求量为通过二次指数平滑法预测出的2023-2025共3年的需求量之和。为了便于在二维平面进行定位计算,需要将经纬度坐标转化为平面xy坐标。通过米勒投影法编写相应算法对经纬度进行转化。由于经纬度转化的坐标数值太大,导致点与点的差距很小,不便于求解和结果分析,于是将横纵坐标分别减去1个公共值,横坐标减去33000,纵坐标减去7300。

5.2 备用仓储中心选择

长三角地区涵盖三省一市,区域不同,城市众多。因此,考虑该地区具体地理情况及位置信息,使用K-means算法将该地区进行聚类的运行结果如图2所示。由图2可知,K-means聚类算法将长三角地区中心城市分为3个区域并得到3个聚类中心,聚类中心坐标依次为(141.9501km,247.0279km)(388.7333km,243.5720km)(522.8903km,433.4988km),将这些聚类中心作为备选仓储中心。

图2 K-means聚类算法运行结果Fig.2 K-means clustering algorithm running results

通过对比K-means、K-modes、K-medians聚类算法,来验证K-means聚类算法在划分区域和计算备用仓储中心方面的优越性及正确性。还运用弗洛伊德算法得出各区域聚类中心到区域内各点的距离和,其值越小,代表聚类算法性能越卓越。3种聚类算法进行对比,结果如表4所示。

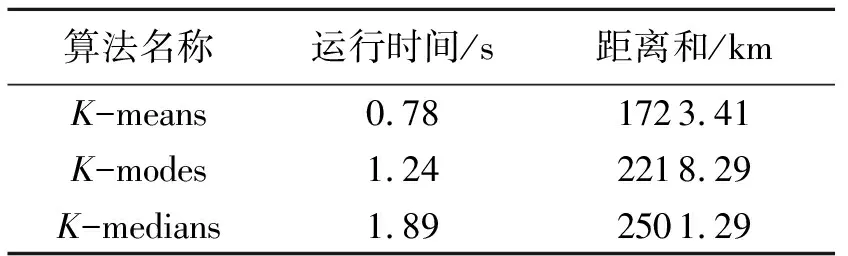
表4 聚类算法比较Tab.4 Comparison of clustering algorithms

由表4可知,K-means聚类算法运行时间最短,距离和最小,这证明该算法相比于其他算法具有优越性,因此可用于选择长三角地区备用仓储中心。通过对比发现,K-means聚类算法的总距离和比其他算法低得多,这说明其可以降低长三角地区物流距离,提高物流效率。

5.3 长三角地区仓储中心选址

通过遗传算法和长三角地区数据集,可以有效地确定物流仓储中心的位置。结合长三角地区具体地理位置,发现该地区中心城市地形紧凑,备选仓储中心覆盖范围较大。因此,为降低仓储中心建设成本,从3个备选中心里挑选出2个,并利用遗传算法和数据集,结合经纬度信息,进行仿真实验,以获得更精准的结果。仿真实验迭代过程如图3所示,得出的仓储中心及对应服务的需求点如图4所示。并与模拟退火算法[12]、蚁群算法[13]进行对比,以总成本为标准,分析判断遗传算法在长三角地区仓储中心选址问题上是否具有科学性及合理性,算法性能对比结果如表5所示。其中对于仓储中心的建设成本及运营成本,根据文献[14]进行取值,3个备选中心的建设及运营成本之和分别为5.2×104、5.0×104、5.1×104元。

图3 迭代过程Fig.3 Iterative process

图4 最优选址方案Fig.4 Optimal site selection scheme

表5 算法性能对比Tab.5 Algorithm performance comparison

由图3可知,算法经过不断优化,使得总成本不断变小直至得到最优结果。当迭代至66次时下降至最低点,在66次之后总成本趋于稳定,最优的总成本收敛于1.8928×108元。

由图4可知,1～9号需求点选择①号仓储中心,10～27号需求点选择②号仓储中心,满足模型成本最小。

由表5可知,相比于模拟退火算法与蚁群算法,遗传算法得出的总成本最小、所用时间最短,这说明通过遗传算法得出的仓储中心可以大大降低长三角地区物流成本。遗传算法在求解长三角地区仓储中心选址问题上具有科学性与优越性,可以为该地区仓储中心选址提供较好的帮助。

6 结论

为提高长三角地区物流效率,助力该地区经济高速发展。提出了运用二次指数平滑法预测长三角地区中心城市2023-2025年货物运输量,以此作为选址依据并建立该地区仓储中心选址模型。利用K-means聚类算法进行区域划分并选出备选仓储中心,使用遗传算法求解选址模型,得出精确的仓储中心坐标位置。通过算法对比,验证遗传算法在解决长三角仓储中心选址问题上具有优越性和科学性,使得该地区物流成本降低,物流效率提高。通过预测未来3年该地区物流量,确定了该地区仓储中心,为仓储中心选址提供了新思路。在未来的研究中,可以预测5年或更长时间的物流量,以此提高仓储中心的可持续性。