静止无功补偿器的小波神经网络PID控制方法研究

周晓华,冯雨辰,王月武,蓝会立

(广西科技大学自动化学院,广西 柳州 545616)

0 引言

近年来,随着大容量电力电子技术的不断成熟,静止无功补偿器(static var compensator,SVC)等动态无功补偿装置在电力系统中得到了广泛应用。随着系统容量的增大与接入电压等级的提升,SVC在输电领域的应用和发展极为迅速[1]。SVC在提高系统动态无功支持[2-4]、直流融冰无功补偿[5]、抑制电压波动[6]和控制交流母线电压[7-8]、改善高压直流输电系统运行稳定性及抑制换相失败[9]、提高系统静态和动态稳定性[10]等方面具有一定优势。

传统的比例积分微分(proportional integral differential,PID)控制结构简单且易于在工程中实现,在SVC控制中占据着主导地位。然而,由于PID控制器参数不能随动态过程实时改变,控制性能往往达不到最佳状态。因此,对用于SVC控制系统的PID控制器结构改进及参数优化成为研究热点。文献[11]将模糊控制和PID控制相互切换的双模控制应用到SVC控制系统中,但模糊规则及模式切换的误差范围需借助运行经验才能确定。文献[12]采用蚁群优化算法对比例积分(proportional integral,PI)控制器参数进行寻优,但蚁群算法存在计算量大、收敛速度慢、易陷入局部最优等缺点。文献[13]采用改进单纯形加速算法对非线性PI控制器参数进行寻优,但单纯形加速算法存在迭代次数多、收敛速度慢等问题。文献[14]在传统PID控制器上增加二阶微分环节,并采用反向传播(back propagation,BP)神经网络对控制器参数进行优化。但其控制算法相对复杂,增加了运算负担。文献[15]在非线性神经元PID控制器上加入二阶微分环节,并采用改进神经元学习算法对控制器参数进行优化。但其控制算法涉及参数较多,不易确定参数值。文献[16]采用比例控制和神经元模型设计变结构PID控制器,并用神经元在线调整变结构PID控制器参数。但变结构误差限的确定仍需依赖工程经验。

反向传播比例积分微分(back propagation proportional integral differential,BPPID)控制利用BP神经网络的自学习能力,可实现增量式PID控制器参数的自动整定功能。但BP神经网络存在收敛速度慢、易陷入局部最优、学习能力和泛化能力差等问题。小波神经网络(wavelet neural network,WNN)采用可缩放平移的小波基替代神经元的线性或非线性激励函数,结合了小波变换的时频局部特性和神经网络的自学习能力。WNN结构简单、收敛速度快,具有规避盲目性的优势[17]。小波神经网络比例积分微分(wavelet neural network proportional integral differential,WNNPID)控制充分利用WNN强大的纠错能力和自学习能力,可有效提高系统的控制性能[18]。本文基于带电流反馈的SVC电压稳定控制策略,采用WNNPID控制设计了SVC的控制器。

本文在Matlab/Simulink仿真平台进行了建模和仿真,并与BPPID控制的控制效果进行了对比,验证了所设计WNNPID控制器的可行性和优越性。

1 SVC控制原理

对于晶闸管投切电容器(thyristor switched capacitors,TSC)+晶闸管控制电抗器(thyristor controled reactor,TCR)型SVC,通常采用带电流反馈的电压稳定控制策略[19-20]。SVC控制系统原理如图1所示。

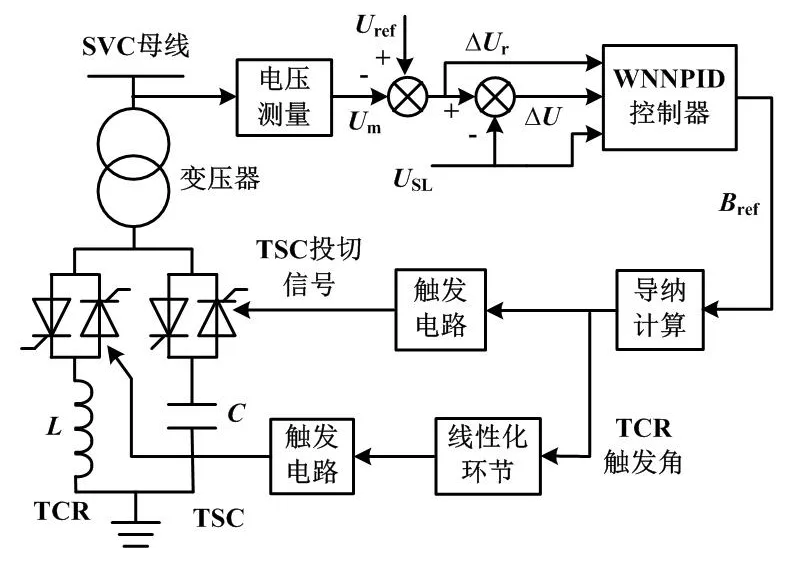
图1 SVC控制系统原理图

图1中:Uref为SVC母线的参考电压;Um为SVC母线电压的均方根值,其值通过电压测量环节获得;USL为SVC的补偿电压,USL=XSISVC。其中:XS为斜率阻抗;ISVC为SVC的输出电流。本文选择电压差ΔUr=Uref-Um、电压误差ΔU=Ur-USL和补偿电压USL作为WNNPID控制器的输入信号,SVC的参考电纳Bref作为输出信号。导纳计算模块由Bref计算TCR触发角α的大小并判断TSC的通断状态,通过线性化和触发电路产生触发脉冲,对TCR和TSC支路的晶闸管进行控制,以实现SVC向系统注入无功功率的连续平滑调节。

通过对多条TSC支路的分组投切并与TCR支路相配合,可维持SVC向系统注入的、电网负荷侧需要的以及电网供给的无功功率之间的平衡,从而达到稳定系统电压的目的。

SVC向系统注入的无功功率可按式(1)计算:

(1)

式中:QC为TSC输出的容性无功功率;QL为TCR输出的感性无功功率;C为TSC支路电容;U为SVC母线电压;L为TCR支路电感。

进一步整理式(1),可得:

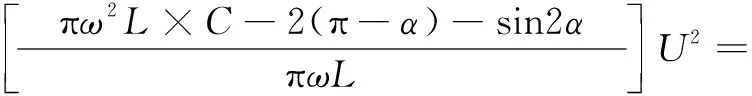
BSVCU2

(2)

式中:BSVC为SVC的等值电纳。

由式(1)和式(2)可知:

(3)

式中:BC为TSC的基波电纳;BL为TCR的等值基波电纳。

综上可知,SVC控制系统通过调节α的大小变化并进行TSC支路的投切,可连续改变SVC的等值电纳BSVC,进而调节SVC向系统注入的无功功率QSVC的大小,以起到调节和控制母线电压的作用。

2 WNNPID控制器设计

WNNPID控制器主要由增量式PID控制和WNN两部分组成。基于WNNPID的SVC电压控制结构如图2所示。

图2 基于WNNPID的SVC电压控制结构图

增量式PID控制器的输入为电压误差信号ΔU(k),输出为SVC的参考电纳Bref(k)。

Bref(k)=Bref(k-1)+ΔBref(k)

(4)

式中:Bref(k)、Bref(k-1)分别为k时刻、(k-1)时刻的参考电纳; ΔBref(k)为k时刻参考电纳的变化量。

ΔBref(k)可表示为:

ΔBref(k)=Kp(k)[ΔU(k)-ΔU(k-1)]+Ki(k)ΔU(k)+Kd(k)[ΔU(k)-

2ΔU(k-1)+ΔU(k-2)]

(5)

式中:Kp(k)、Ki(k)和Kd(k)为k时刻增量式PID控制器的比例系数、积分系数和微分系数;ΔU(k)、ΔU(k-1)、ΔU(k-2)分别为k时刻、(k-1)时刻和(k-2)时刻的电压误差。

根据SVC系统的运行状态,增量式PID控制器参数Kp(k)、Ki(k)和Kd(k)由WNN实时进行在线调整。WNN结构如图3所示。

图3 WNN结构图

三层WNN采用4-5-3结构。其中:输入信号为ΔUr(k)、USL(k)、ΔU(k)和1;输出信号为Kp(k)、Ki(k)和Kd(k)。

输入层与隐含层间的权值为wij(k)。隐含层神经元的激励函数φ(·)采用Morlet小波基函数,则隐含层的输出可表示为:

(6)

(7)

隐含层与输出层间的权值为wjl(k),输出层激励函数g(·)采用Sigmoid函数,则输出层的输出为:

(8)

(9)

为实现权值wij(k)和wjl(k)的更新,定义误差函数为:

(10)

按照梯度下降法调整网络权值,其调整式[21]为:

(11)

式中:α′为惯性系数;η为神经元的学习率。

根据式(11)可得到隐含层与输出层间权值wjl(k)调整的具体算法为:

(12)

其中:

(13)

(14)

输入层与隐含层间权值wij(k)调整的具体算法为:

(15)

其中:

(16)

WNNPID控制算法的具体步骤[22]如下。

①初始化。设定WNN输入层节点数i、隐含层节点数j及输出层节点数l,并设定权值初始值wij(0)、wjl(0)以及惯性系数α′、学习率η、尺度变换因子aj、伸缩因子bj的值。

②采样得到Uref(k)、USL(k)和Um(k),并计算电压差ΔUr(k)和电压误差ΔU(k)。

④按照式(4)和式(5)计算WNNPID控制器输出的控制量,即SVC的参考电纳Bref(k)。

⑤WNN学习。按照式(12)～式(16)在线调整权值wij(k)和wjl(k),以实现PID控制器参数Kp(k)、Ki(k)和Kd(k)的自适应调整。

⑥令k=k+1,返回步骤②。

3 仿真与结果分析

为验证WNNPID 控制算法的可行性和有效性,本文采用Matlab/Simulink仿真平台进行仿真。系统由短路容量6 000 MVA、735 kV的可编程电压源、线路及200 MW负荷串联组成。SVC通过1台735 kV/16 kV、333 MVA变压器并联在负荷侧。SVC 由1条TCR支路和3条TSC支路构成。其中:TCR支路为109 MVar;每条TSC支路为94 MVar。

与WNNPID不同,BPPID的BP神经网络隐含层神经元的激励函数采用正负对称的Sigmoid函数[23]。其隐含层的输出为:

(17)

WNN和BP神经网络参数如表1 所示。

表1 WNN和BP神经网络参数

SVC参考电压Uref=1.0 p.u.,斜率阻抗XS=0.01 p.u./100 MVA。在0～0.05 s时,系统电源电压保持1.0 p.u.不变。在0.05 s时,系统电源电压突增至1.025 p.u.。在0.2 s时,系统电源电压突降至0.93 p.u.。在0.35 s时,系统电源电压恢复至1.0 p.u.。3种控制器的电压UM控制效果对比曲线如图4所示。

图4 电压UM控制效果对比曲线

在控制器的控制下:在0～0.05 s时,UM=1.0 p.u.保持不变;在0.05 s电源电压突增时,UM被调高至1.01 p.u.;在0.2 s电源电压突降时,UM被调低至0.974 p.u.;在0.35 s时,电源电压恢复至1.0 p.u.,UM被调回至1.0 p.u.。由图4可知,WNNPID和BPPID控制器的响应速度较快,控制效果均优于PI控制器。WNNPID的电压控制效果最好。

SVC注入系统无功对比曲线如图5所示。

图5 SVC注入系统无功对比曲线

在0～0.05 s时,如电源电压保持1.0 p.u.不变,SVC向系统注入的无功为0。在0.05 s电源电压突增时,SVC切除TSC支路,TCR支路吸收约100 MVar的无功以调低UM。在0.2 s时,电源电压突降,SVC投入TSC支路并向系统注入约250 MVar的无功以调高UM。在0.35 s时,电源电压恢复至1.0 p.u.,SVC再次切除TSC支路,向系统注入的无功减少至0。由图5可知,与其他2种控制器相比,WNNPID控制下的SVC可更快速地吸收或补偿系统的无功功率。

SVC投入TSC支路条数变化曲线如图6所示。

图6 SVC投入TSC支路条数变化曲线

在0～0.05 s时,电源电压保持1.0 p.u.不变,n=1,TSC1支路投入运行。通过与TCR相配合,SVC向系统注入的无功功率为0。在0.05 s时,电源电压突增,n从1变为0。此时TSC1支路被切除、TCR支路吸收系统多余的无功功率。在0.2 s时,电源电压突降,n按0→1→2→3变化。此时,TSC1、TSC2和TSC3支路依次投入运行,SVC向系统注入的无功功率迅速增加。在0.35 s时,电源电压恢复至1.0 p.u.,n按3→2→1变化。此时,TSC3、TSC2支路依次被切除,SVC向系统注入的无功功率大大减少。由图6可知,与PI控制相比,BPPID和WNNPID 控制下的SVC均能迅速地投入或切除TSC支路,实现了无功功率的快速补偿和调节。并且,WNNPID控制时的TSC支路具有更快的投切速度。TCR触发延迟角变化曲线如图7所示。

图7 TCR触发延迟角变化曲线

通过与3条TSC支路的投切相配合,TCR支路可用于吸收系统多余的无功功率,并较好地实现了SVC对母线电压的稳定控制作用。

BPPID和WNNPID控制器参数变化曲线如图8所示。

图8 BPPID和WNNPID控制器参数变化曲线

由图8可知,WNN和BP神经网络均较好地实现了PID控制器参数的在线自适应调整功能。与传统PI控制相比,由于PID控制器参数可根据SVC的动态过程实时变化,在一定程度上改善了SVC控制系统的控制性能。

4 结论

WNNPID控制器同时兼顾了PID控制器和WNN控制的优点,具有较强的自适应能力。其用于SVC控制系统,可满足SVC的动态无功补偿和母线电压调节的需求。通过研究,本文可得到以下结论。

WNNPID控制算法不依赖于被控对象的精确数学模型,控制算法简单且需要确定的参数较少。其PID控制器参数Kp、Ki和Kd由WNN在线自适应调整,并随SVC的动态过程实时改变,无需考虑PID控制器参数初始值的确定问题。与传统PI控制相比,WNNPID控制算法可有效改善SVC控制系统的动态响应性能。

WNN将BP神经网络隐含层神经元的激励函数由正负对称的Sigmoid函数改为Morlet小波基函数,可充分利用小波变换的时频局部特性和神经网络的自学习能力,收敛速度较快。与BPPID控制相比,将WNNPID用于SVC的电压控制可获得更好的控制效果。