具有扰动项的双曲守恒律系统的PI反馈与稳定性分析

赵东霞, 鲍芳霞

(中北大学数学学院, 太原 030051)

双曲型分布参数系统在数学及其它各领域中一直有着广泛的应用,很多运输现象和流动现象均可用双曲型偏微分方程来描述.如:热交换器模型,生物种群模型,交通流模型,渠道模型等等[1-4].近年来,一阶双曲型偏微分方程受到专家学者的广泛关注,尤其致力于研究它的控制器设计和稳定性分析.对于双曲型系统的控制问题,工程上通常采用PI(比例积分)或PID(比例积分微分)控制器,通过调整反馈参数,使柯西问题的解收敛到一个期望的平衡态上[5-6].对于双曲型系统的稳定性分析,主要有特征根分析法和Lyapunov函数法[7-8].文献[9]针对拟线性双曲系统,利用特征根分析法,建立了系统沿着特征曲线的解的指数稳定性.对于带有非齐次项的双曲守恒律系统,文献[10]结合黎曼坐标变换、特征线和李雅普诺夫函数方法研究了系统的鲁棒性问题.文献[11]针对具有一般形式的二维双曲守恒律系统,首先采用黎曼坐标变换将其对角化处理,然后构建了一个严格的李雅普诺夫函数,并证明在某个参数条件下,李雅普诺夫函数对时间的导数严格负定,从而验证系统的指数稳定性.文献[12]针对一类非线性双曲偏微分方程,构造显式二次李雅普诺夫函数作为稳态小扰动的加权函数,通过选择适当的边界反馈控制,得到在H2范数下系统的局部指数稳定性.针对一阶运输方程:

∂tr(t,x)+λ∂xr(t,x)=0,t∈[0,∞),x∈(0,L),

(1)

其中,r(t,x)表示t时刻、x位置处的系统状态,λ>0表示系统的特征速度.文献[13]研究了系统(1)在PI边界反馈控制器下的稳定性以及系统达到稳定时的参数取值范围和相应的时滞容许区间.此外,基于庞特里亚金定理,得出无论参数如何选取,系统(1)在PID边界反馈控制器下总是不稳定的结论．

受上述文献的启发,本文研究如下带有非齐次扰动项的一维双曲守恒律系统:

∂tr(t,x)+λ∂xr(t,x)=r(t,x),

t∈[0,∞),x∈(0,L),

(2)

其中,r(t,x)表示在时刻t、位置x处的系统状态,λ>0为常数,表示系统的特征速度.该系统可以刻画种群生态学中生物种群受年龄结构影响的现象,从而反映种群的现实状况并推测种群的发生、发展过程．

对于系统(2),考虑具有如下形式的PID边界反馈控制器:

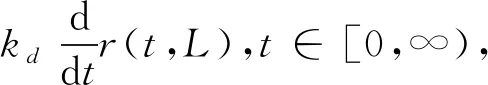
(3)

其中,kp,ki,kd分别表示比例、积分、微分反馈控制参数.特别地,当kd=0时,PID边界反馈控制器(3)退化为PI边界反馈控制器,即:

(4)

另外,本文还将进一步研究如下形式的向量守恒律系统:

(5)

在PI控制器

(6)

下的稳定性问题．

本文主要针对文献[13]在文末中所提出的开放性问题“对于具有扰动项或者向量形式的双曲守恒律系统,是否可以采用类似的办法对其分析”进行详尽讨论.对于具有非齐次项的一维标量守恒律系统(2)和一维向量守恒律系统(5),采用特征根分析法,讨论了系统在PI和PID边界反馈控制下的稳定性,建立了系统参数的稳定性区域,确定了时滞参数的稳定区间．

1 一维标量守恒律系统的稳定性分析

本节将分析系统(2)、(4)及系统(2)、(3)的稳定性．

1.1 系统(2)在PI控制器(4)下的稳定性分析

1.1.1 特征多项式的建立 首先,利用特征线法计算系统(2)的解．

该系统的特征方程为

(7)

特征线为

x-λt=C.

(8)

作变量替换

ξ=x-λt,η=t.

(9)

此时,

(10)

则系统(2)化为

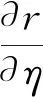
(11)

对η积分得通解

r=eηg(ξ)=etg(x-λt),

(12)

其中,g为具有一阶连续导数的任意函数.不妨设初始条件为t=0∶r=y(x),则有

t=0∶r=g(x)=y(x),

(13)

从而系统(2)的形式解为

r(t,x)=ety(x-λt).

(14)

将(14)代入到边界条件(4)中,得到特征多项式为

(15)

系统(2)在PI控制器下所得的特征多项式(15)是含有一个指数项的超越多项式,为了分析闭环系统(2)(4)的稳定性,即分析式(15)的所有零点是否位于复平面的左半平面,故引入单时滞系统的Walton-Marshall稳定性准则．

1.1.2 单时滞系统的Walton-Marshall稳定性准则 对于单时滞系统,其特征多项式可表示为

c(μ)=f(μ)+g(μ)e-τμ,

(16)

其中,μ∈C表示系统的特征值,f(μ)与g(μ)是互素的实系数多项式,记f(μ)和g(μ)的次数分别为p,q,且p≥q．

单时滞系统的Walton-Marshall稳定性准则分为下面三个步骤(详见文献[14]第五章和文献[15])．

1) 分析时滞τ=0时的参数稳定性条件．

2) 分析时滞从0增加到τ>0时,特征值μ是如何变化的.根据f(μ)和g(μ)的次数可分为以下两种情况.

当p>q时,系统特征多项式的所有零点均位于复平面的左半平面内,不会发生稳定性的切换．

当p=q时,系统特征多项式的根可能穿过虚轴,此时考虑纯虚根μ=iω,ω∈R.利用共轭复数的性质,如果μ=iω是c(μ)=0的根,则-μ=-iω也是c(μ)=0的根.将μ=iω代入特征多项式(16)中并消去指数项,得到一个关于ω2的实系数多项式,用P表示:

P(ω2)=f(iω)f(-iω)-g(iω)g(-iω).

(17)

对于充分大的ω,只要实系数多项式

P(ω2)>0

(18)

成立,则单时滞系统是指数稳定的．

3) 确定P的正根和时滞τ的容许区间,以及当τ增加时这些根是稳定的还是不稳定的.首先考虑方程P(ω2)=0是否存在正实根y=ω2,如果没有,那么不会发生稳定性切换,即:若无时滞情形下系统是稳定的,则当τ>0时系统将始终保持稳定.如果方程P(ω2)=0有正实根,则必然会导致特征方程有纯虚根,从而使得系统的稳定性发生切换.此时,利用特征方程f(iω)+g(iω)e-iωτ=0,若g(iω)≠0,得到时滞τ满足

(19)

求得时滞τ的临界值后,进而分析当τ持续增大时,特征根是否从左半平面穿过虚轴进入右半平面,从而判断系统是稳定的还是不稳定的．

注1文献[15]还指出,对于非负根y≥0,如果P′(y)<0,则P是稳定的;如果P′(y)>0,则P是不稳定的.这里′表示的是对y求一阶导数．

1.1.3 系统(2)(4)的稳定性分析 接下来,利用单时滞系统的Walton-Marshall稳定性准则进行分析．

1) 当τ=0时,特征多项式(15)变为

(1-kp)(1-μ)=ki,

(20)

即

(21)

此时,无时滞系统指数稳定当且仅当

(1-kp)(1-kp-ki)<0,

(22)

即

1-kp<0,1-kp-ki>0,

(23)

或

1-kp>0,1-kp-ki<0.

(24)

2) 在式(15)中,多项式f(μ)和g(μ)的次数p=q=1,故考虑纯虚根μ=iω,ω∈R+.此时,多项式(17)变为

P(ω2)=f(iω)f(-iω)-g(iω)g(-iω)=

(kp+ki-ikpω)(kp+ki+ikpω)-(1-iω)(1+iω)=

(25)

显然,当且仅当

|kp|>1

(26)

时,对充分大的ω,P(ω2)>0．

3) 确定P的正根和对应的时滞临界值．

由(25)和(26)可得,当且仅当

|kp+ki|<1

(27)

时,多项式P存在正根,记作

(28)

此时,由(19)可得

(29)

则

(30)

解得

j=0,±1,±2,….

考虑到τ>0,ω0>0,于是,

min{τ}≐τ0=

(31)

其中,

(32)

定理1设边界反馈参数kp,ki满足条件(22)和(26),进而,

1) 若|kp+ki|≥1,则对∀τ>0,系统(2)、(4)均稳定;

2) 若|kp+ki|<1,则系统(2)、(4)稳定当且仅当τ∈(0,τ0),其中,τ0的定义见(31)式．

1.2 系统(2)在PID控制器(3)下的稳定性分析

系统(2)在PID控制器(3)下的特征方程为

c(μ)=-[kd(1-μ)2+kp(1-μ)+ki]+

(1-μ)e-μτ=0,

(33)

这属于Walton-Marshall稳定性准则中p>q的情形．

首先考虑极限情形τ=0,(33)退化为

-[kd(1-μ)2+kp(1-μ)+ki]+(1-μ)=0,

(34)

即

kd(1-μ)2+(kp-1)(1-μ)+ki=0.

(35)

于是,

(36)

其中,

Δ1=(kp-1)2-4kdki.

(37)

显然,当且仅当如下三个条件:

(B1) Δ1≤0,kd(2kd+kp-1)<0;

(38)

之一成立时,无时滞系统指数稳定.于是,结合Walton-Marshall稳定性准则得如下定理．

定理2系统(2)、(3)对任意的τ>0均稳定当且仅当(38)中三个条件之一成立．

2 一维2×2双曲守恒律系统的稳定性分析

本节分析一维2×2向量守恒律系统(5)在PI控制器(6)下的稳定性．

类似1.1.1小节,利用特征线方法可求得系统(5)(6)的特征多项式为

c(μ)=(1-μ)(1+μ)-

(39)

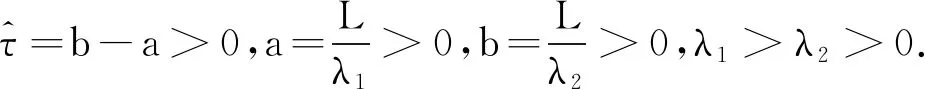
接下来利用1.1.2部分单时滞系统的Walton-Marshall稳定性准则分析(39)的零点分布.结合(16)式,多项式f(μ)和g(μ)分别取为

f(μ)=1-μ2,

g(μ)=-[k3(1-μ)+k4][k1(1+μ)+k2].

(40)

(1-μ)(1+μ)-

[k3(1-μ)+k4][k1(1+μ)+k2]=0,

(41)

即

(k1k3-1)μ2-(k1k4-k2k3)μ-

(k1+k2)(k3+k4)+1=0,

(42)

解得

(43)

其中,

Δ2=(k2k3-k1k4)2-4(k1k3-1)·

[1-(k1+k2)(k3+k4)].

(44)

根据一元二次方程的性质,当且仅当

(C0) 1-(k1+k2)(k3+k4)≠0

(45)

及如下五个条件:

(C3) Δ2≤0且k1k4-k2k3>0,k1k3-1<0;

(C4) Δ2≤0且k1k4-k2k3<0,k1k3-1>0;

(C5)k1k3-1=0且(k1k4-k2k3)(k1k4+k2k3+k2k4)>0

(46)

之一成立时,无时滞系统是指数稳定的．

2) 由(40)知,多项式f(μ)和g(μ)的次数均为2,故不妨考虑纯虚根μ=iω,ω∈R+,此时,多项式(17)变为

P(ω2)=f(iω)f(-iω)-g(iω)g(-iω)=

(1+ω2)2-

1-(k3+k4)2(k1+k2)2.

(47)

显然,当且仅当

|k1k3|<1

(48)

或

(49)

时,对充分大的ω,P(ω2)>0．

注2易知,针对情形(48),仅可取(46)中的条件(C1)或(C3)成立.针对情形(49),仅可取(46)中的条件(C1)、(C3)或(C5)成立．

3) 确定P的正根以及当τ增加时这个根是否稳定．

下面分两种情形展开讨论.

①针对情形(48),令y=ω2>0,由(47)可得

(50)

其中,

(51)

为方便讨论,设如下条件:

(C6) Δ3<0;

(C7) Δ3≥0且y1,2<0;

(C8) Δ3≥0且y1,2>0;

(C9) Δ3≥0且y1>0,y2<0.

(52)

如果参数满足条件(C6)或(C7),则P(ω2)=0无正根.如果参数满足条件(C8),由于

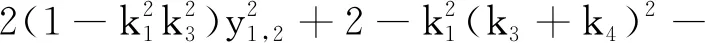
(53)

所以y=y1这个较大根是不稳定的,而y=y2是稳定的根.如果参数满足条件(C9),结论类似可得.进而,考虑到

(54)

则

(55)

于是,

(56)

(57)

其中,

(58)

②针对情形(49),此时,

1-(k3+k4)2(k1+k2)2.

(59)

于是,

(60)

是P(ω2)=0的唯一解.如果

(k3+k4)2(k1+k2)2-1>0,

(61)

则y=ω2为唯一正解,且容易验证,这是稳定的正根.否则,P(ω2)=0无正根．

综上分析,得出如下定理．

定理3假设边界反馈参数满足条件(C0):(k3+k4)(k1+k2)≠1．

1) 若ki满足条件(48),且条件(C1)或(C3)成立,则

①当(C6)或(C7)之一成立时,对∀τ>0,系统(5)(6)均稳定;

2) 若ki满足条件(49),且条件(C1)、(C3)或(C5)之一成立,则对∀τ>0,系统(5)、(6)均稳定．

注3对于系统(5),考虑如下的PID控制器:

(62)

则相应的特征多项式为

c(μ)=(1-μ)(1+μ)-

[k6(1-μ)2+k3(1-μ)+k4][k5(1+μ)2+

k1(1+μ)+k2]e-μτ,

(63)

f(μ)=(1-μ)(1+μ),

g(μ)=-[k6(1-μ)2+k3(1-μ)+k4][k5(1+μ)2+

k1(1+μ)+k2].

(64)

显然,f的次数小于g的次数,故Walton-Marshall稳定性准则不再适用．

3 数值仿真

本节将利用MATLAB工具进行数值模拟,进一步说明系统(2)和系统(5)在PI控制器和PID控制器下的动力学性质．

例1对于系统(2),设

取(4)中边界反馈参数为

kp=2,ki=-2,|kp+ki|=0<1,

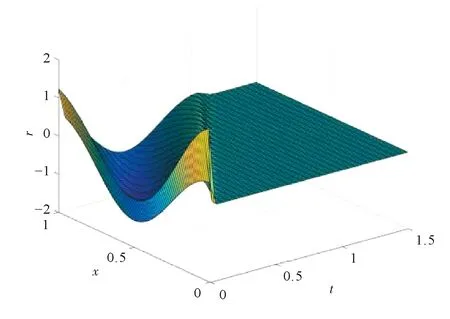
图1 r(t,x)在系统(2)、(4)中的收敛性

例2对于系统(2)(3),取边界反馈参数为

kp=-2,ki=2.25,kd=1,

此时满足条件

(B1) Δ1=0且kd(2kd+kp-1)=-1<0,

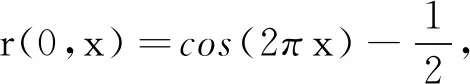
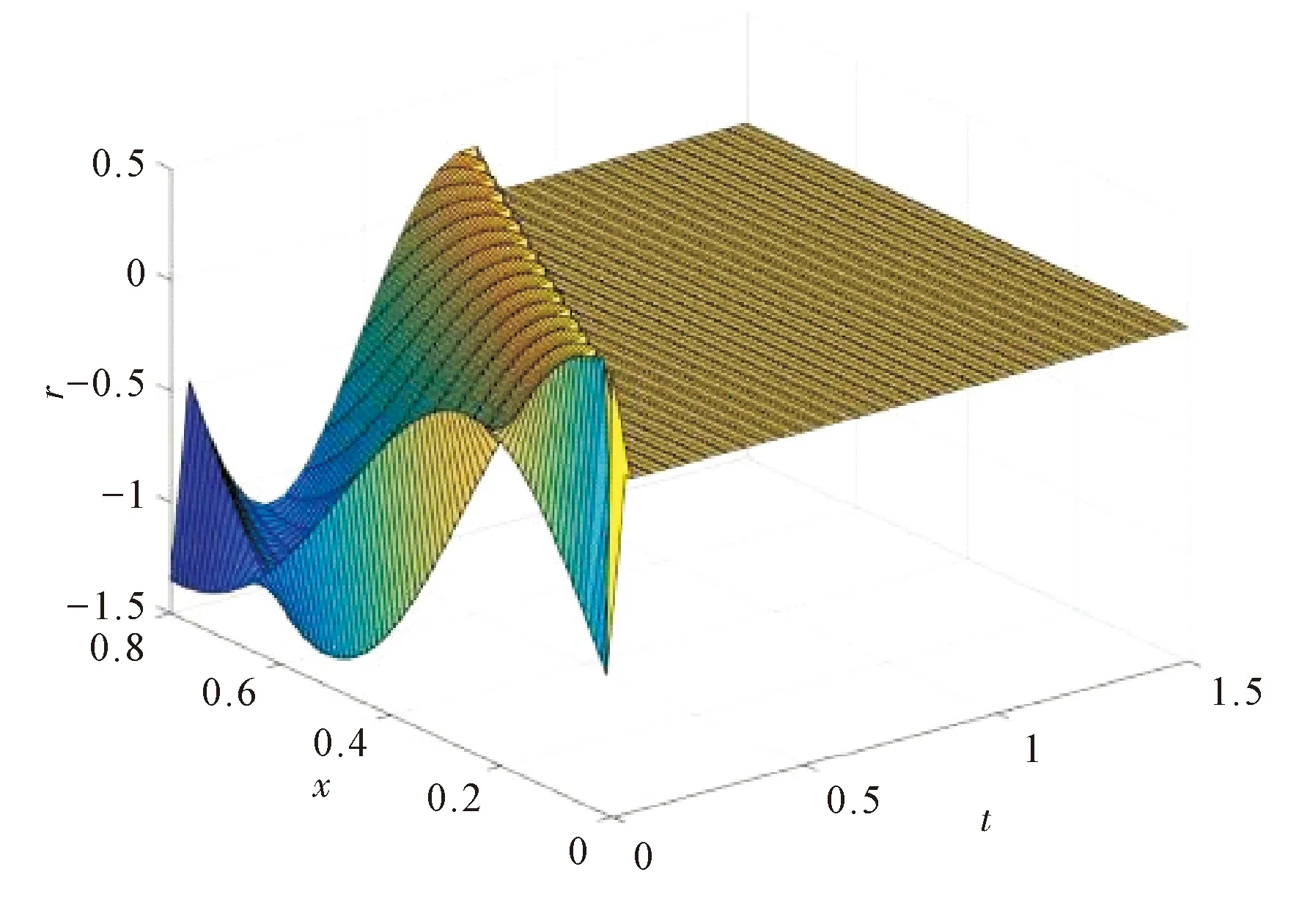
图2 r(t,x)在系统(2)、(3)中的收敛性

例3对于系统(5)(6),取边界反馈参数为

k1=1,k2=2,k3=0.3,k4=1,

此时满足条件

(C0):(k3+k4)(k1+k2)=3.9≠1,

且满足条件

|k1k3|=0.3<1,

以及条件

(C3): Δ2=(k2k3-k1k4)2-4(k1k3-1)[1-(k1+k2)(k3+k4)]=-7.96<0,且k1k4-k2k3=0.4>0,k1k3-1=-0.7<0;

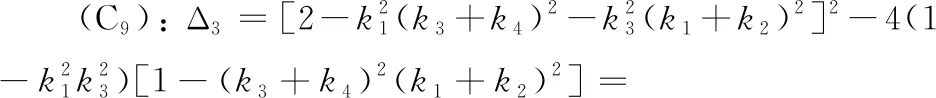
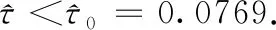
图3 r(t,x)在系统(5)、(6)中的收敛性

4 结论

本文首先建立了具有非齐次扰动项的双曲型偏微分方程(组)系统,利用特征线方法得到其形式解,并结合PI/PID边界反馈控制条件计算特征多项式.其次,采用Walton-Marshall稳定性准则分析系统的稳定性条件,得到了反馈参数的耗散性条件以及相应的时滞容许区间;最后,采用Matlab数学软件仿真进一步佐证结论的合理和有效性．