VG 模型参数对边坡稳定性系数影响的敏感性分析

王乐 WANG Le；汪洋 WANG Yang

（①鄂北地区水资源配置建设与管理局（筹），武汉 430062；②孝感市孝南区应急管理局，孝感 432001）

0 引言

敏感性分析是指当我们对模型进行数值模拟时，模型参数的变化对模拟结果的影响程度，判断各个模型参数对模型结果的重要程度[3]。当前，对边坡稳定性分析中主要考虑的因素有土体容重γ、粘聚力c 及内摩擦角φ，如彭小云等[4]基于灰度关联分析法分析了影响高边坡稳定的因素，结果显示重力及滑动面的强度参数是影响边坡稳定的主要因素。VG 模型方面国内研究主要是VG 模型的应用及参数的获取。其中范严伟等[5]利用HYDRUS-1D 模型，分析了不同土壤条件下VG 模型中饱和含水量、残余含水量、系数及饱和渗透系数对土壤水分特征曲线的影响，发现系数和饱及渗透系数n 与湿润锋运移距离成正相关，而系数a 及残余含水量与湿润锋成负相关。徐付桥等[6]研究了VG 模型参数的选取对碱水层二氧化碳封存的影响。杨红等[7]基于VG 模型研究了有机肥对土壤水分特征曲线的影响，表明VG 模型可以较好拟合土壤水分特征曲线。田东方等[8]研究了尿素浓度对土壤水分特征曲线的影响，建立了可以考虑尿素浓度影响的VG 模型。彭建平等[9]提出了一种用MATLAB 确定VG 模型参数的方法。

本文利用Carsel and Parrish（1988）[10]文章中砂土、粉土、粉质粘土的VG 参数，然后将原参数上调10%、20%以及下调10%、20%，以GEO-sudio 软件分析VG 模型中系数n、α、饱和含水量θs、残余含水量θr以及饱和渗透系数Ks，5 个因素对边坡中土体稳定性系数的影响，并通过正交试验设计分析进行VG 模型参数敏感性分析。

1 基本理论

1.1 渗流基本理论

本文以GEO-studio 软件为主，GeoStuio 软件是加拿大专业的岩土分析软件，由Fredlund 教授20 世纪70年代开始研发。GEO-studio 中渗流公式为Richards 方程，对于一维非饱和土壤水分运动，Richards 方程常表示为3 种形式，即以压力水头、以含水率和以位置坐标为因变量的公式，下面给出以压力水头h 表示的非饱和渗流方程[11]：

式中：kij—分别沿水平及垂直方向的渗透系数，m/s；ρw—水的密度，g/cm3—土壤水特性曲线的斜率；且，其中θw—含水量；uw—水压力，kPa。

1.2 极限平衡法基本理论

GEO-studio 软件中SLOPE/W 模块采用通用刚体极限平衡法。该方法由Fredlund 等人于20 世纪70年代提出。特点是假设每个土条的受力平衡，每个土条安全系数相等。同时满足力矩、水平力、竖向力的平衡。通用极限平衡法力矩平衡安全系数方程：

水平方向静力平衡安全系数方程：

式中：c′—有效粘聚力；φ′—有效摩擦角；u—孔隙水压力；N—土条底部法向力；W—土条重量；D—集中荷载；β、R、x、f、d、w—几何参数；a—土条底面倾角。其中N 为土条底部的法向力。

云计算是为了解决用户的存储资源不足和共享资源不足问题，将大量的服务器资源通过网络整合和调度重新分配给用户。高校之间、校内老师之间由于受到技术、知识产权等客观因素的影响，课程资源很难实现共享，还可能有课程资源重复建设的现象，基于云计算技术的网络教学平台在充分保护知识产权的情况下实现了跨地区的教学资源同步共享，通过彼此协商和网络确认实现相互间教学资源共享和学习交流[2]。

式中：XR、XL—土体两侧的剪切力。当土为非饱和时，有效粘聚力c 取值如下：

1.3 VG 模型

VG 模型是1980 由Van Genuchten 提出的一种土壤水分特征曲线的模型[1]，到现在已经广泛应用于地下水分析、渗流分析以及各类软件中。VG 模型表达式[1]：

1.4 正交实验设计

正交实验设计的本质是一种数理统计方法，首先确定有代表性的点，然后根据正交表进行多因素实验。其正交表表示为：Ln（tm），式中：L—正交表；n—正交试验次数；t—影响因子的水平数；m—正交试验表列数。

正交试验表格完成后，就是进行数据分析；正交试验计算数据分析的一般方法有：极差分析法和方差分析法。极差分析方法简单、快捷、方便，不足之处是精度，只能定性分析；方差分析于极差分析而言精度要好，但相应的计算要复杂一些。本文采用极差分析方法进行计算。

极差分析方法的计算统计参数公式为[12]：

式中：Kij—影响因子j 在i 水平下每次试验结果的平均值；n—影响因子j 在i 水平下的正交试验次数；Yk—第k 个正交实验的值；—所有试验的平均值。

设极差分析法的敏感性评价标准为Si，则其计算公式为：

Sj越大，则该影响因子越大，反之。

2 VG 模型参数对边坡稳定参数的敏感性分析

2.1 模型概况

通过《工程地质手册（第四版）》表3-1-24 得到砂土、粉土和粉质黏土的物理参数，模型参数如表1，模型如图1。

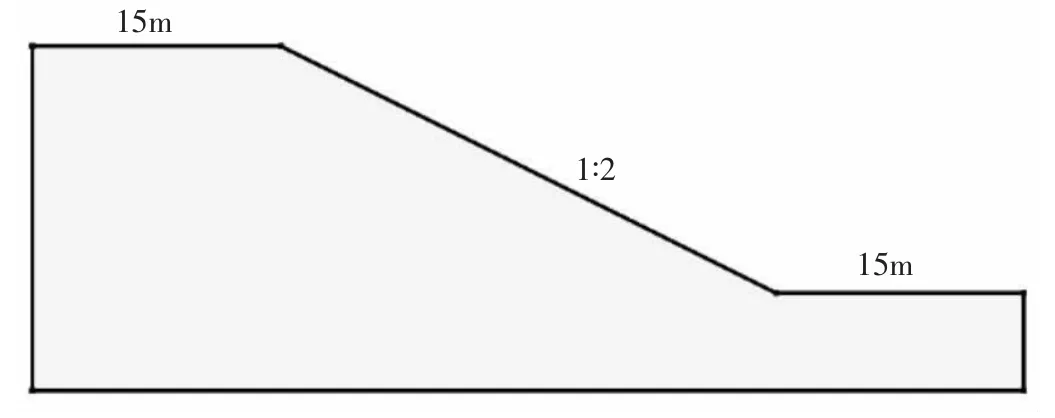
图1 边坡模型

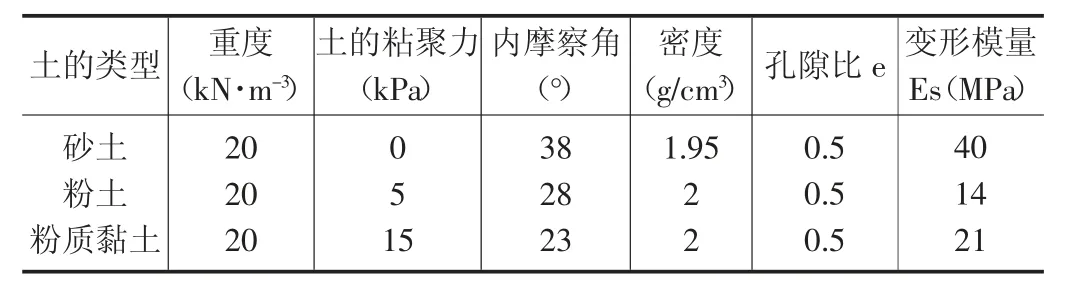
表1 模型参数

边坡模型边坡底长60m，左高21m，右高6m，坡高10m。其余参数如图1 所示。图中模型全局网络单元尺寸为1m，网格四边形与三边形一共826 个单元，892 个节点。

2.2 参数θr、θs、α、n 以及Ks 的扰动对边坡稳定影响

根据Carsel and Parrish（1988）[5]得砂土、粉土及粉质黏土，以砂石为例对其VG 参数进行微调得到其正交实验水平取值如表2。

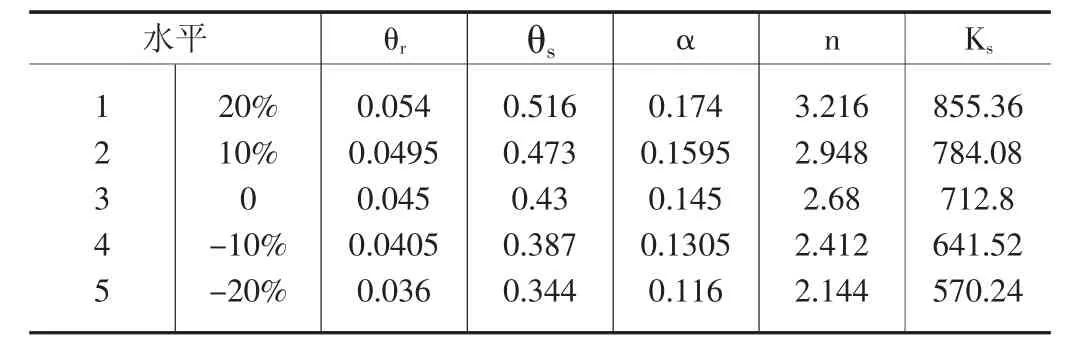
表2 正交试验因素水平取值

由于本文是5 因素5 水平，这里选择L25（56）正交表，使用GEO-studio 软件计算边坡的安全系数，其正交表及计算结果见表3。

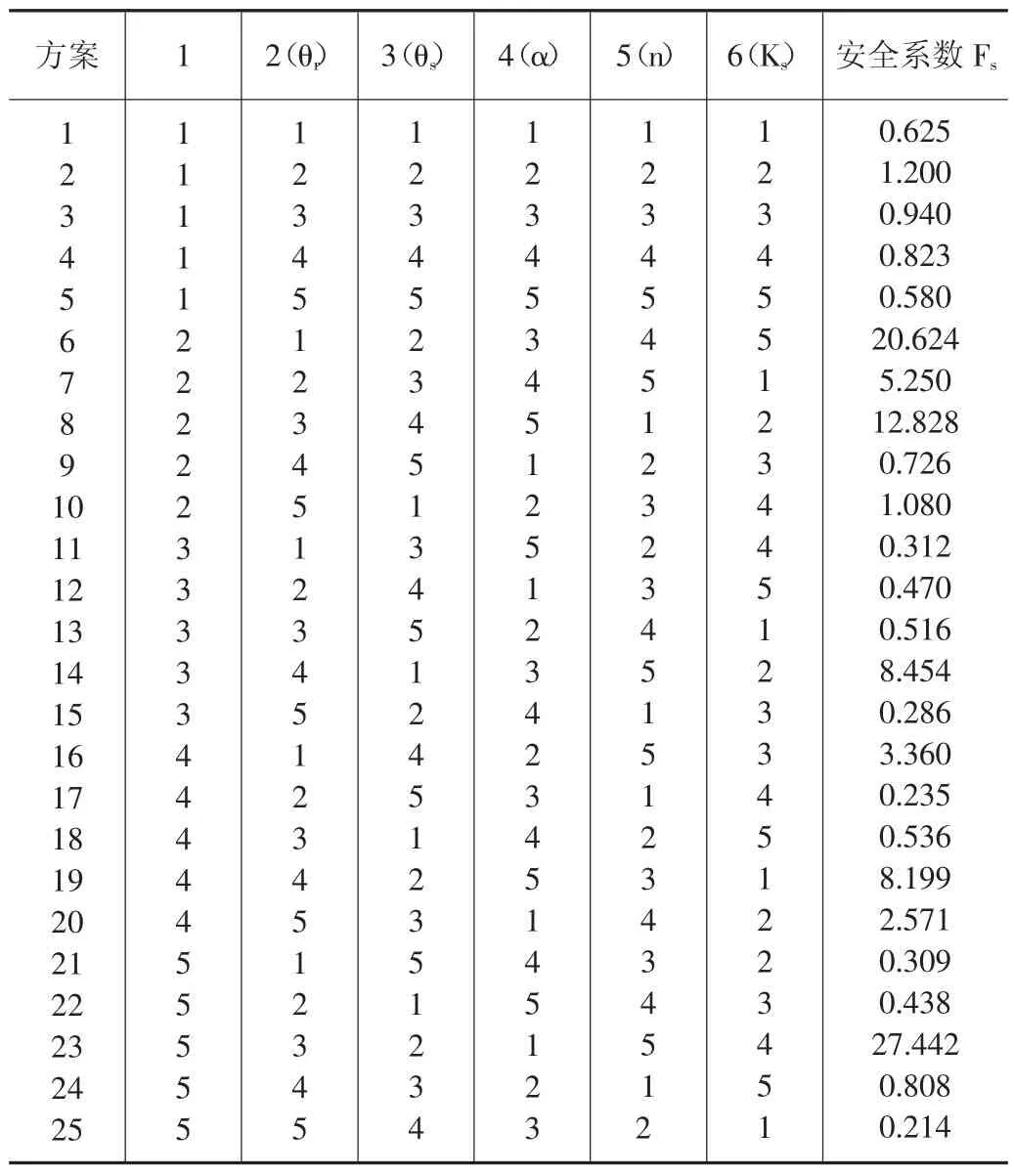
表3 砂土正交设计方案及安全系数结果

通过对正交表数据分析计算得到极差分析方法数据如表4 所示。

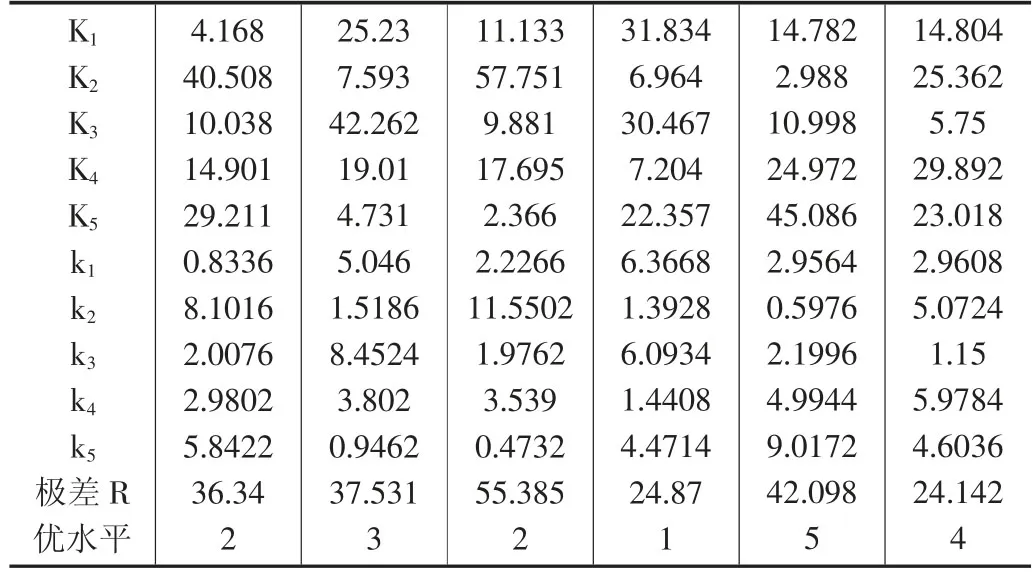
表4 砂土极差分析表

通过对极差分析方法表可以看出：在砂土中，VG 模型中饱和含水量θs对边坡稳定性系数影响最大，其次是系数n，再次是残余含水量θr，然后是系数α，对边坡稳定性系数影响最小的则是Ks。

同理得到粉土的极差分析表如表5。

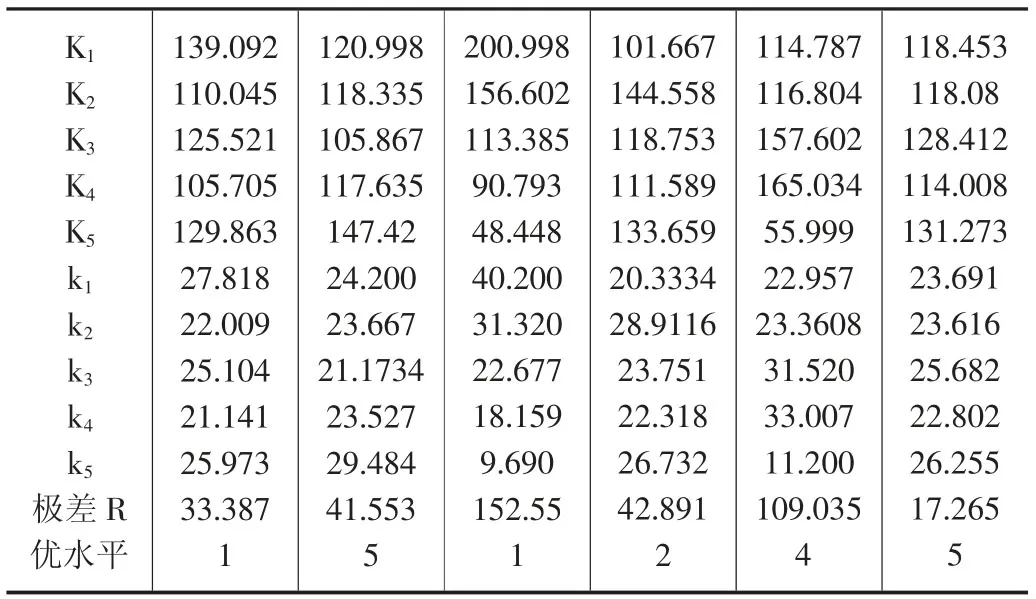
表5 粉土极差分析表

通过上面的正交试验可以知道对于粉土，VG 模型中饱和含水量θs对边坡稳定性系数影响最大，系数n 次之，再次是系数α，饱和渗透系数Ks和残余含水量θr对边坡稳定性系数影响最小。

对于粉质黏土由于VG 模型参数n＞1，所以只有3 组水平，即5 因素3 水平，这里使用L18（37）正交表，其余过程同砂石一样，算得粉质黏土极差分析表如表6。

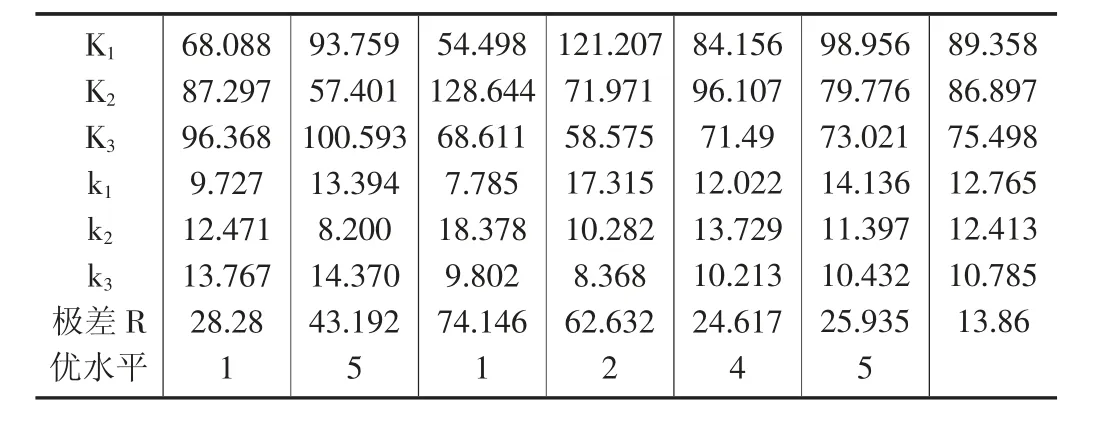
表6 粉质黏土极差分析表

通过极差分析表可以得到：对于粉质黏土，残余含水量θr对边坡稳定性系数影响最大，然后是饱和含水量θs，再次是系数n，最后是系数α，饱和渗透系数Ks。

对砂土和粉土，VG 模型参数中的饱和含水量θs和系数n 的扰动对边坡的稳定性系数影响较大；系数α、饱和渗透系数Ks和残余含水量θr对边坡稳定性系数影响较小。对粉质黏土，则是残余含水量θr和饱和含水量θs的扰动对边坡稳定性系数影响较大；系数n、最后是系数α 以及饱和渗透系数Ks的影响较小。造成这样结果的原因可能是：砂土与粉土的粘聚力小，水在下渗的过程中砂土和黏土的粘聚力有一个增大的过程，然后随着水下渗量的增加砂土与粉土的粘聚力才开始减小；而对于粉质黏土其粘聚力较大，因此水在下渗过程中粉质黏土的粘聚力直接就开始减小。

VG 模型在这里可以发现主要是影响土中水的分布以及土中各处的水头，从而对边坡的稳定性造成影响。本文通过对正交试验验证了VG 模型参数对边坡稳定性系数的敏感度，具有一定的工程实际意义。

3 结语

本文选取了砂土、粉土和粉质黏土的VG 模型参数，研究了其VG 模型参数的扰动对边坡稳定性的影响，通过GEO-sudio 软件模拟得到不同VG 系数下边坡的安全系数，设计L25（56）及L18（37）正交试验表分析各个系数的扰动对边坡稳定性影响，得到敏感度关系，对于砂土是：θs>n>θr>α>Ks；粉土：θs>n>α>Ks>θr；粉质黏土：θr>θs>n>α>Ks。即对砂土和粉土，VG 模型参数中的饱和含水量θs的扰动对边坡的稳定性系数影响最大；系数n 次之，系数α、饱和渗透系数Ks和残余含水量θr对砂土和粉土边坡稳定性系数影响较小。对粉质黏土而言，则是残余含水量θr的扰动对边坡稳定性系数影响最大；饱和含水量θs次之，再次是系数n，最后是系数α 以及饱和渗透系数Ks的影响较小。