HJC 模型参数确定及隧道光面爆破炮孔间距优化

侯飞

（中铁四局集团有限公司第七工程分公司，合肥 230000）

0 引言

近年来，我国交通工程建设得到了迅猛发展，隧道特别是长大隧道的建设与研究取得了长足的进步[1-2]。钻爆法作为一种安全、经济、快速有效的施工方法，目前已在国内外隧道与地下工程建设中得到了广泛应用[3]。在隧道建设过程中，爆破方案的选择是隧道开挖效果主要因素，直接影响隧道掘进的效率和开挖成本。

在隧道掘进过程中，围岩的力学性质会有所变化。因此盲目套用现有的爆破孔网参数，会造成爆破掘进的效率低下以及火工品等材料的浪费。因此，本文首先基于现场取样与室内试验对HJC 本构模型参数进行了标定，然后基于LS-DYNA 有限元软件建立不同孔间距离的数值模型，对炮孔间距进行了优化研究，最后将数值模拟的结果在玉皇山隧道工程上进行了验证。

1 工程概况

玉皇山隧道进口位于山东省烟台市海阳市留格庄镇境内，出口位于威海市乳山市乳山寨镇境内隧道穿越两地区交界段落，全长6058m，隧址区最高海拔约422m，最大埋深约377.9m，采用无轨运输双车道断面，地下水主要为构造裂隙水，富水性较好，围岩稳定性差，基岩以花岗岩为主，围岩等级主要以Ⅳ级围岩为主。

隧址区属于暖温带东亚季风型大陆气候区，四季分明，气候温和。累年平均降雨量813mm，累年平均相对湿度为70%。设计方案设计采用全断面施工，掘进方法采用钻爆法施工，设计的单次装药炮孔总数为170 个，循环进尺为3.2m，如图1 所示。现场作业时发现，该爆破方案存在炮孔数量过多、炸药用量过大、超挖严重等现象。

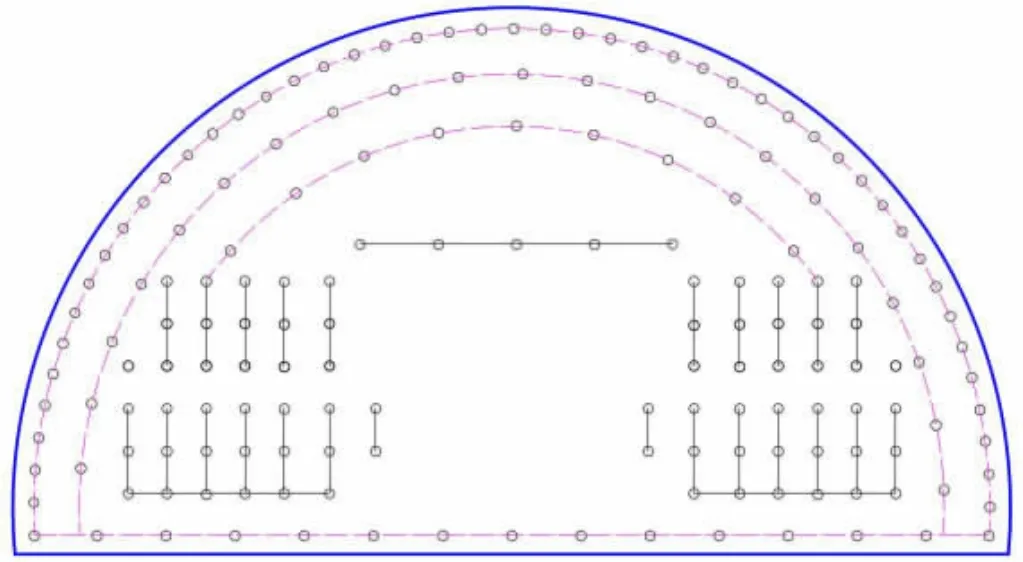
图1 炮孔布置

2 花岗岩本构模型及参数确定

2.1 HJC 模型简介

HJC 模型可以很好地描述岩石类材料在动态冲击过程中的大变形问题。HJC 模型将岩石类材料的等效强度表示为压力、应变率和损伤的函数，广泛应用于数值计算中。HJC 模型主要包括屈服面方程、状态方程和损伤方程。HJC 模型主要包含21 个参数，本文将这些参数分为四组：基本物理参数、屈服面参数、状态方程参数和损伤参数。基于相关实验和文献结论来确定这些参数。

2.2 基本物理参数

花岗岩的基本物理参数主要通过进行相应的物理试验来获取。对花岗岩试件进行单轴压缩与三轴压缩试验，得到了试件的基本力学参数，即单轴抗压强度σc=148.5MPa；弹性模量E=74.5MPa，剪切模量G=31.04GPa，密度ρ=2.67g/cm3，最大拉伸静水压力T=15.1MPa；泊松比v=0.20。

2.3 强度模型参数确定

材料归一化的等效强度具体表达式为：

式（1）中：σ*是无量纲等效应力；σ 为实际等效应力；P*表示标准化静水压力，P*=P/fc，P 为实际静水压力；fc为准静态单轴抗压强度；为无量纲应变率，（其中为真实应变率值；为参考应变率，可取值为1.0s-1）；D 为损伤度（0≤D≤1.0）；A、B、C、N 为材料的强度参数。

2.3.1 参数C 确定

应变率系数C 用来表征材料的应变率强化效应，可以通过材料的静态以及动态抗压强度计算得到。动态抗压强度一般通过霍普金森压杆（SHPB）试验得到。因此需要对花岗岩试件进行SHPB 试验，得到不同应变率下试件的动态抗压强度。在动态载荷的作用之下，岩石类材料的动态强度抗压强度会发生提高，主要受静水压力以及动态强度增强因子共同作用，因此在确定参数C 值时，首先需要排除静水压力的影响。参照相关文献，作-T（1-D）点与各动态抗压强度点之间的直线，在P*=1/3 处作平行于纵轴的直线并与不同应变率下的直线相交于4 个点。得到消除了静水压力的归一化等效应力值，将交点处归一化等效应力值和对应的应变率数据进行线性拟合，作出以σ*为纵坐标，以为横坐标的曲线，拟合直线的斜率即为应变率系数C 的值，C=0.0063。

2.3.2 参数A、B、N 的确定

在不考虑损伤和率效应时，HJC 极限面方程式为：

根据相关研究，HJC 模型与Mohr—Coulomb 模型在压缩子午面上均经过纯剪切和单轴压缩等相关的特征点。据此可得到粘性强度系数A、粘聚力c 与单轴抗压强度fc之间的相关关系，即A=c/fc。

通过三轴压缩试验得到了准静态时（应变率10-4s-1时）第一主应力和第三主应力之间的关系，通过M—C 准则拟合试验结果可以得到第一主应力σ1和第三主应力σ3之间的函数关系如式（3）所示：

已知Mohr—Coulomb 准则：

式中，θ 为内摩擦角，c 为粘聚力。

联立式（1）～式（3）可得，c=23.09，θ=49.25°。当P=0 时，根据公式，A=c/fc，此时可得到准静态时，即ε.=10-4s-1粘性强度系数A=0.155。将其归一化到.*=1.0 时，得到A=0.155+C（1-1n10-4）=0.19。

不考虑损伤和率效应时，HJC 模型强度表达式为：

式中：σ*是表示归一化等效应力；P*归一化静水压力。在三轴压缩试验中，可以按照式（6）-式（7）计算：

每一个三轴压缩实验数据点和σ*-P*平面上的点相互对应，通过数据拟合的方法即可得到B=0.79 和N=1.05，如图2 所示。

图2 等效强度与静水压力之间的关系

Sfmax表示σ*可以达到的最大值。在大多数的参数敏感性分析中，Sfmax被归为不敏感参数。据此，本文对参数Sfmax仍采用原始文献提供的数据，即Sfmax=7.0。

2.4 状态方程参数的确定

HJC 模型的状态方程用来表述静水压力p 与体积应变μ 之间的关系。状态方程可以分为三个阶段，即弹性阶段、塑性变形阶段和压实阶段。

第一阶段，线弹性阶段，即0≤p≤pc，此时静水压力和体积应变之间呈线性相关关系，其状态方程表达式为：

式中：K 为材料的体积模量，K=E/3（1-2v），v 为材料的泊松比在弹性阶段，压碎压力pc=fc/3=49.5MPa，压碎应变μc=pc/K=0.0012。

第二阶段，塑性变形阶段，即pc≤p≤pl。此时材料内部的孔洞裂隙逐渐被压实发生不可逆的塑性损伤破坏，此阶段的状态方程可表示为：

其中：μp为与压实静水压力pl对应的体积变形。

第三阶段，压实阶段，即pl＜p。此阶段内材料发生破坏，曲线呈非线性变化。其状态方程可表示为：

式中，K1、K2、K3为压力常数，μ=（μ-μ）l（/μ+μ）l，为锁定体积应变，μ 为体积应变，μl为压实极限时的体积应变，表示为：μl=ρ/ρ0-1，其中ρ0为初始密度，ρ 为压实密度，参照文献，ρ=2.77g/cm3；计算得μ=0.0036。材料压力参数K1、K2、K3、Pl的取值可通过Hugoniot 实验数据获得，由于Hugoniot 实验的成本较高。因此，一般采用LosAlamos 国家实验室所做的各类岩石材料Hugoniot 实验数据或者经验公式，如式（11）所示：

其中：C0和S 是经验常数，对于花岗岩，C=2100m/s-1和S=1.63。对材料密实阶段的压力参数进行拟合，如图9所示。根据拟合结果得到K1=15GPa，K2=62GPa，K3=77GPa。

2.5 损伤模型

HJC 损伤模型由等效塑性应变和塑性体积应变来表示，损伤演化公式可表示为：

式中：Δεp为单位循环发生的等效塑性应变，Δμp表示单元的塑性体积应变；分别表示常压破碎等效塑性应变和塑性体积应变，εfmin为材料发生破坏时最小塑性应变，εfmin、D1、D2表示损伤常数。由文献可知，参数εfmin和对数值模拟结果影响很小，εfmin和D2值分别为0.01 和1。D1由下式计算：

式中：p*为归一化静水压力，T*为归一化抗拉强度，满足等效断裂应变时，p*=1/6，由于压力较低，故令μfp=0，带入求得D1其值为0.03。如表1 所示，超高性能混凝土HJC本构模型参数全部确定。

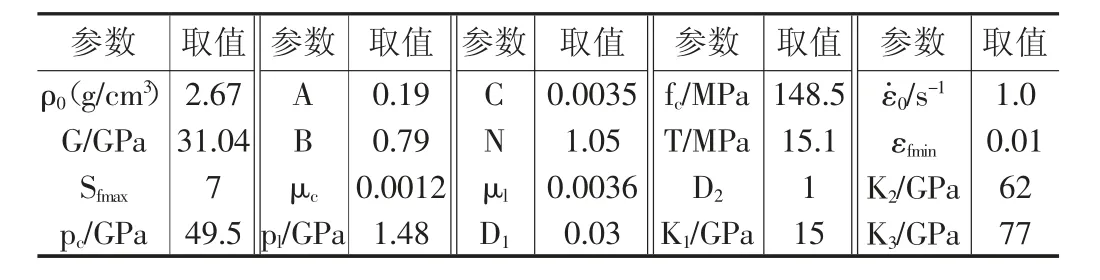
表1 材料计算参数

3 炮孔间距的优化

3.1 算法选择

LS-DYNA 具有强大的流体与固体相互耦合的功能，因此被广泛应用于爆炸、冲击等分析中。模型中三种材料均采用SOLIED164 单元映射网格划分，固体单元即岩石采用Lagrange 单元算法，流体单元（炸药、空气）采用Ale算法，采用*CONTROL_ALE 来控制流固耦合的相关控制，炸药与岩体之间通过关键字*CONSTRAINED_LAGRA NGE_IN_SOLID 来进行连接，实现流体－固体耦合的动态分析。

3.2 结果分析

如图3 所示，应力波从炮孔中心向四周传播过程中会在炮孔中心形成拉应力，当拉伸应力值大于岩石动态抗拉强度时，会在两炮孔间出现裂隙，随着应力波的传播，孔间的裂纹逐渐贯通，从裂纹的贯通程度来看，当炮孔间距小于85cm 时，炮孔之间的裂纹完全贯通；随着炮孔间距的增大，即当炮孔间距为90cm 时，炮孔之间未发生贯通。

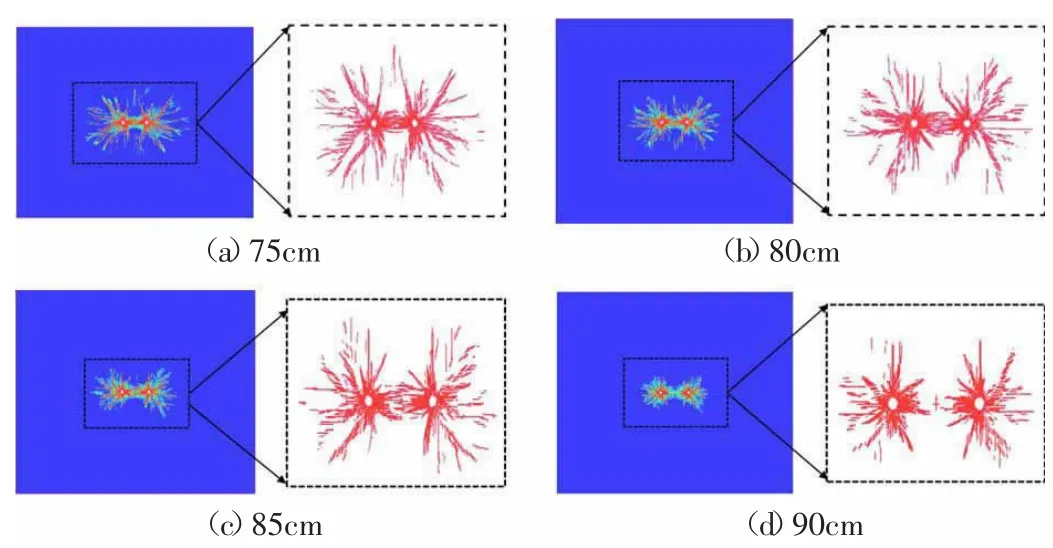
图3 孔间拉应力曲线

提取各工况下两炮孔间中心单元的拉应力峰值，如图4 所示，不同孔距孔间拉应力在100μs 左右到达峰值，分别为38MPa、35.6MPa、32.0MPa、28.6MPa。可见，中心单元拉应力之随炮孔间距增加而降低。当炮孔间距大于85cm时，拉应力峰值小于28.6MPa，结合损伤云图，说明岩石的动态抗拉强度应大于28.6MPa，小于32.0MPa。

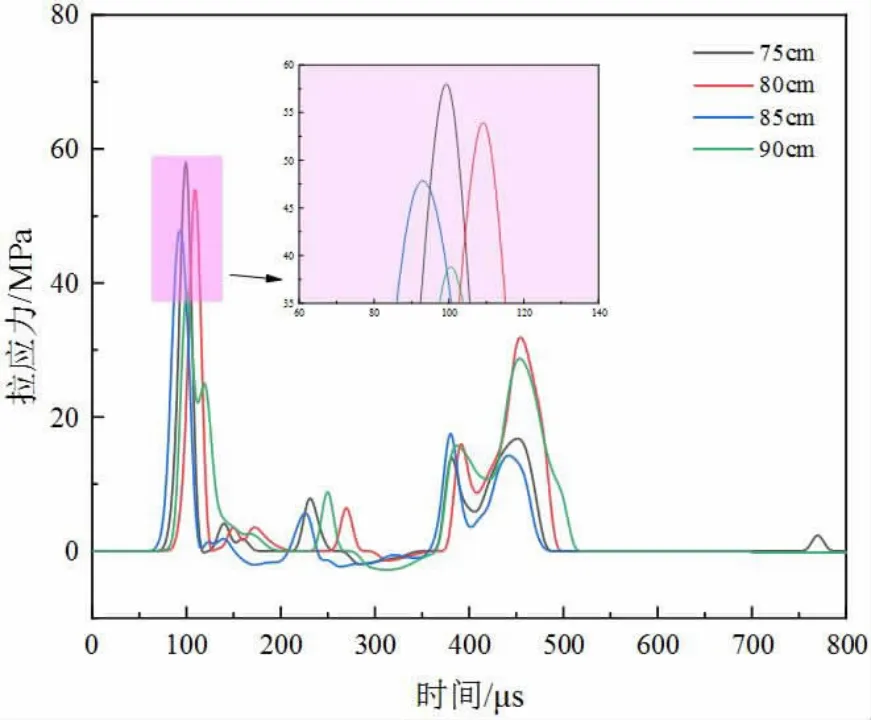
图4 孔间拉应力曲线

综合以上分析同时兼顾爆破形成岩体块度等因素，两个炮孔中点处拉应力峰值宜超过28.6MPa；炮眼间距取85cm 左右较为合理，这时可避免岩体因受到拉应力产生粉碎性破坏，既降低了能量浪费，也能对岩体进行有效的拉裂。

3.3 周边孔爆破分析

调整孔间距后，进行现场试验，如图5 所示，发现炸药爆炸后在爆炸应力波与爆生气体联合作用下周边各炮孔之间已经形成了较为完善的贯穿裂缝。爆破完成后，隧道开挖轮廓线和设计轮廓线吻合较好。最大超挖量0.13m、断面总超挖面积0.69m2，爆破效果较好。

4 结论

为了提高光面爆破的质量，减少围岩的超欠挖，基于数值模拟对于炮孔间距进行了优化。结果表明：①HJC 模型可以较好地模拟岩石在冲击荷载下的动力学特性，但模型参数较多，通过单轴压缩与三轴压缩实验确定了花岗岩的HJC 模型。②随着炮孔间距的增大，炮孔之间裂纹的贯通程度逐渐降低。当炮孔间距小于85cm 时，炮孔间的损伤可以有效贯通。大于85cm 时，两孔之间的未能形成贯通裂隙，因此炮孔间距选择80～85cm 最佳。③数值模拟结果和现场试验结果表明：本文采用的流固耦合方法、岩石本构模型以及材料的选取可以较为准确地描述岩石类材料在爆破荷载作用下的损伤特性。