浮置板轨道沿线砖混建筑物振动响应及楼内振动传播规律

刘 悦，谭新宇，姜博龙，刘冀钊，陈江雪

（1.交通运输部科学研究院，北京 100029；2.中国铁路设计集团有限公司城市轨道交通数字化建设与测评技术国家工程研究中心，天津 300308）

0 引言

截至2022 年底，我国内地已有53 座城市开通运营城市轨道交通线路，线路总长9 584km[1]，其中，地铁占比高达八成。城市轨道交通蓬勃发展的同时，地铁线路不可避免会下穿文教区、居民区等人口密集区域，地铁列车运行引发的建筑物振动及二次噪声问题，对沿线居民正常生产生活产生了不利影响[2-4]。因此，研究地铁线路沿线建筑物振动响应规律具有重要的现实意义。

目前，国内外学者多从理论和实测的角度对地铁线路沿线建筑物振动响应及传播规律展开研究。Degrande 等[5]以伦敦地铁为对象，对距地铁线路70 m 的两测点处的地面、建筑物楼面和楼内支承柱的振动响应进行了实测，分析得出楼内振动响应大小与行车速度相关性较小，但楼内振动衰减程度大于室外地面的结论。Lopes 等[6]建立了列车-轨道-隧道-土体数值模型，对列车运行引发的建筑物振动进行了计算分析，发现土体参数的选取对模拟结果的影响较大。Ma 等[7]建立三维有限元模型，计算分析了地铁列车运行对西安钟楼振动的影响，进而对桩基的减振效果进行了预测，并与现场实测结果进行了比对；此外，Ma等[8]还利用三维有限元模型计算了地铁列车通过曲线隧道时，列车振动对周围高层框架结构建筑物的影响。宋波等[9]通过现场实测和数值模拟，研究得出了地铁对沿线砖砌结构振动的影响规律，包括距离、土层条件和隧道埋深等因素对砖混结构振动响应的影响规律，为地铁沿线建筑物的合理改造提供了建议。Cao 等[10]基于波谱单元法，从原理上分析了列车振动在建筑物内的传播规律及特性，发现不同结构形式的建筑物中振动的传播规律并不完全一致，需要有针对性地分析不同建筑物的振动响应传播规律。地铁浮置板轨道作为普遍采用的特殊减振措施，其减振效果评价通常以隧道壁和环境振动为依据，目前关于振动在建筑物内以及不同楼层的衰减程度的研究较少，并且缺乏关于频域内振动衰减规律的研究，因此难以全面系统地从分频角度评估地铁浮置板的减振效果，制约了浮置板轨道的选型设计及合理使用。

针对上述问题，本文以某运营地铁浮置板轨道为背景，建立了地铁列车-浮置板轨道频域耦合解析模型及道床-隧道-地层-建筑物有限元仿真模型，利用实测数据对模型进行校核，并对建筑物进行模态分析。根据计算结果，研究振动在建筑物内不同楼层间的传播衰减规律及各楼层的频域振动特性，以期为减隔振措施的优化设计及合理选用提供依据。

1 模型的建立

在对地铁列车振动环境影响问题进行建模计算分析时，国内外学者多将整个系统分为车辆-轨道子系统和道床-隧道-地层-建筑物子系统[11]，以平衡计算效率与计算精度。具体做法是，利用车辆-轨道子系统计算得出支承反力，以此为激励输入到道床-隧道-地层-建筑物子系统，实现两个子系统的耦合。借鉴这一思想，本文将分别建立地铁列车-浮置板轨道频域耦合解析模型和道床-隧道-地层-建筑物有限元模型，对浮置板轨道沿线建筑物振动响应及传播规律进行计算分析。

1.1 地铁列车-浮置板轨道耦合解析模型

为计算地铁列车通过时钢弹簧浮置板轨道的板下钢弹簧支承反力，为地铁列车运行引发沿线建筑物振动响应的计算提供输入荷载，本文基于文献[12]的思路，建立如图1 所示的二维地铁列车-浮置板轨道频域耦合解析模型。此模型引入无限周期结构理论，可通过计算一块浮置板范围内轨道的振动响应得到无限长轨道中任一点的振动响应，具有计算快速、结果准确的优点。模型中，地铁列车考虑为多节编组列车，单节列车由1 个车体、2 个转向架及4 个轮对构成，考虑车体及转向架的沉浮、点头自由度，以及轮对的沉浮自由度。根据D′Alembert 原理和多刚体理论[14]，在频域内建立单节列车各个部件在各自由度的动力学方程；浮置板轨道中，钢轨及浮置板分别用无限长Euler 梁模型、两端自由的Euler 梁模型进行模拟，扣件和钢弹簧均用弹簧阻尼元件进行模拟。

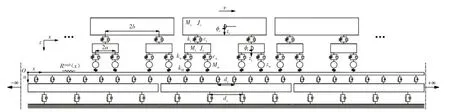
图1 地铁列车-浮置板轨道耦合系统模型[12]

利用轮轨接触关系，获得整辆移动列车的所有动态轮轨接触力后，可进一步求解移动列车通过时浮置板轨道任一点的振动响应，进而得到浮置板下每个钢弹簧的支承反力。具体求解方法参见文献[15]。

根据实际运营线路情况，确定地铁列车为普通6 节编组B 型车，行车速度为60 km/h，采用美国6 级轨道不平顺功率谱模拟轨道不平顺条件。浮置板轨道参数见表1[16]。以上条件下，计算得到的典型板下钢弹簧支承反力如图2所示。

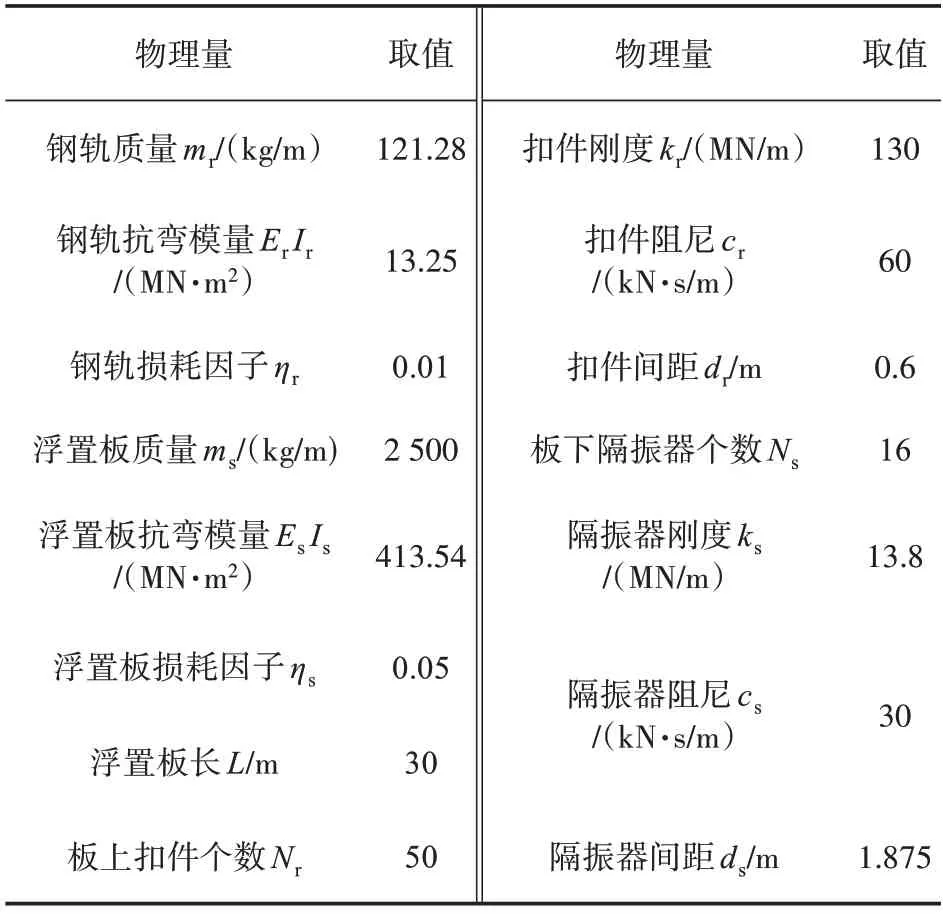
表1 浮置板轨道参数（双轨参数）

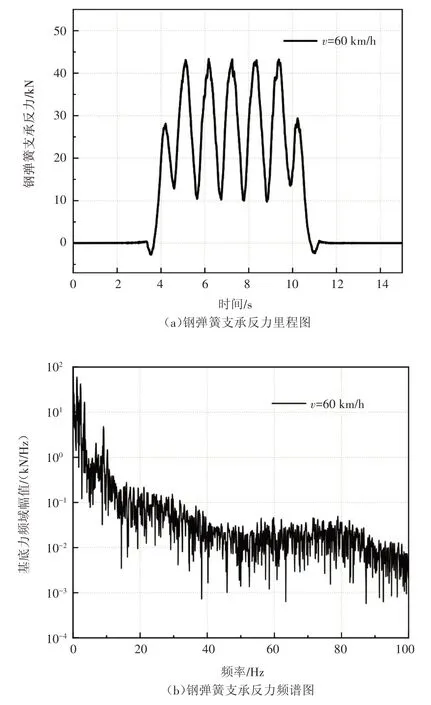
图2 典型板下钢弹簧支承反力

1.2 道床-隧道-地层-建筑物有限元模型

本文涉及的某地铁线路隧道为双洞盾构隧道，轨道形式为钢弹簧浮置板轨道，基底厚度为0.9 m；隧道内径为2.7 m，衬砌厚度为0.3 m，埋深为14.5 m。根据地勘数据确定计算模型中的地层参数如表2所示。

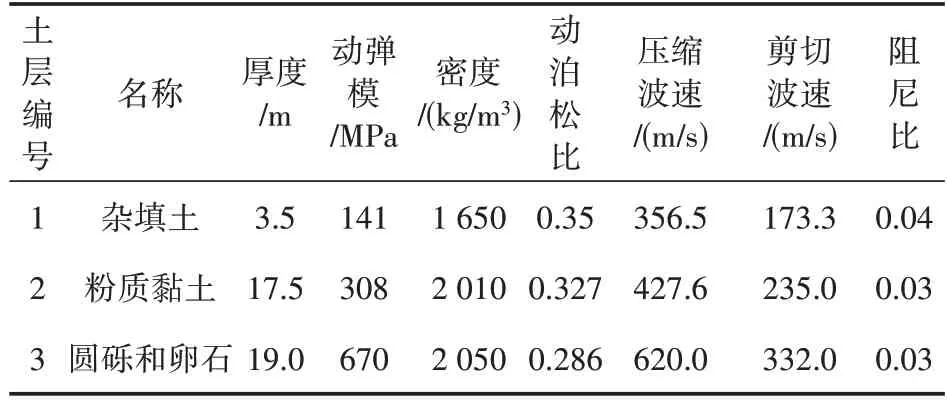
表2 计算模型地层参数

沿线某建筑物为6 层砖混结构，建筑物西侧墙与隧道中心线间的最短距离仅为6 m。图3为其平面图。根据隧道与建筑物的实测相对位置，用MIDAS GTX-NX 软件建立了如图4 所示的道床-隧道-地层-建筑物有限元仿真模型。

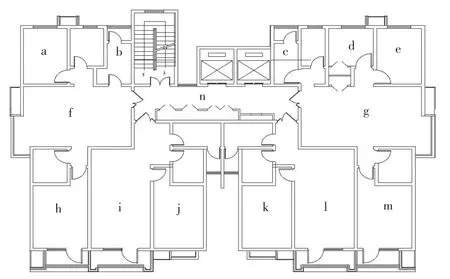
图3 建筑物平面图及各房间编号

图4 道床-隧道-地层-建筑物耦合有限元仿真模型

模型中，混凝土衬砌及建筑物的弹性模量为3.5×1010Pa，泊松比为0.25，密度为2 500 kg/m3；隧道仰拱处混凝土道床的厚度为0.9 m，泊松比为0.3，弹性模量为4.2×1010Pa，密度为2 500 kg/m3。为了平衡计算效率与计算精度，将模型尺寸确定为长100 m、宽40 m、高30 m；采用3D 四面体网格对模型中隧道及土体部分进行划分，基底和隧道壁的网格尺寸为0.3 m，土体由隧道到远场采用0.3 m～0.4 m～1.2 m 的过渡网格，距离隧道越近，网格划分尺寸越小。为消除振动波传播的边界效应，采用自由场单元定义该有限元模型的四周边界。建筑物用1D 和2D 单元模拟，单元尺寸为0.4 m；楼板和墙面用板单元模拟，板厚分别为0.25 m 和0.35 m；梁和柱用梁单元模拟。本模型的关心频率为1～100 Hz，系统的阻尼特性用瑞利阻尼模拟。

利用1.1 节建立的列车-钢弹簧浮置板轨道模型，按实际情况计算列车在隧道范围内移动时所有板下钢弹簧的支承反力，发现各个钢弹簧的支承反力随列车经过该弹簧的先后顺序存在固定的时间差。然后将各个支承反力按实际空间顺序以点荷载的形式对应施加在道床模型中各钢弹簧的固定位置处，即可进行后续计算分析。

1.3 模型计算结果与实测结果对比

将整组钢弹簧支反力以固定点荷载的形式输入道床-隧道-地层-建筑物耦合有限元仿真模型中，计算得到建筑物内各层楼板的振动响应，然后对建筑物内多个房间的振动响应进行实测。图5 所示为距隧道最近的建筑物1 层f 房间中心点处垂向振动加速度1/3 倍频程曲线的实测结果和模拟结果。从图中可知，实测结果与模拟结果在趋势上较为一致，数值上吻合良好，说明应用此模型可保证后续分析的准确性与可靠性，并可进一步研究建筑物内的振动传播规律。

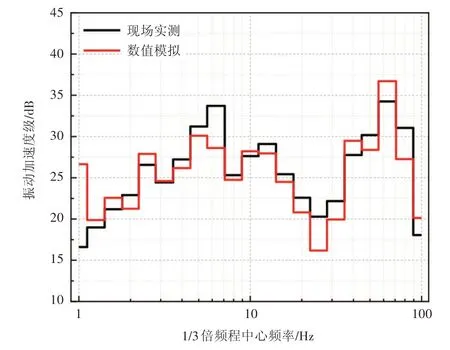
图5 f房间中心点处垂向振动加速度实测值与计算值1/3倍频程曲线对比

2 建筑结构振动响应分析

2.1 建筑物模态分析

本节首先利用有限元软件对建筑物进行模态分析，以明确建筑物的固有振动特性。图6和图7分别给出了建筑物的前3 阶模态振型云图及第1阶垂向振动模态（为第7阶模态）振型云图。表3给出了建筑物的前50阶模态频率。

表3 建筑物前50阶模态频率

图6 建筑物的前3阶模态振型云图

图7 建筑物的第1阶垂向模态振型云图

从图6、图7 和表3 可以看出，由于该砖混建筑物的墙体较薄、层数较少，其质量相对同类结构较小，此时建筑结构的1 阶模态频率出现在13.79 Hz，与同类型结构相比各模态频率稍大。其1 阶～3 阶的模态振型分别为y向（南北向）水平振动振型、x向（东西向）水平振动振型以及绕z轴（建筑物中心竖轴）扭转振动的振型。仅考虑垂向振动并基于理想化刚性结构，该建筑物大约在37.7 Hz（第7 阶模态）时出现第1 固有频率模态（第1 垂向模态）。从图中可以发现，同一楼层不同房间的振动响应大小差异比较明显，并且随着楼层增高，楼板受竖向振动的影响也增大。建筑结构的主要模态振型集中在30～50 Hz，说明建筑结构的振动和二次噪声受此频段振动波的影响较大，对于该频段的振动需要重点关注。

2.2 楼内振动传播规律分析

在明确建筑物固有振动特性后，计算了靠近建筑物一侧地铁列车以60 km/h 的速度（列车通过此断面时的实际运行速度）通过时，建筑物各楼层每个房间地板中心位置处的垂向振动响应。

以顶层为例，根据建筑物模态分析结果可知：h,f 房间距离线路最近，振动响应最大；n 房间位于中间位置，振动响应最小；g 房间距离线路最远，但振动响应也较大。因此，选择h,f,n,g等4 个房间作为典型房间进行后续分析。图8 所示为6 层的这4 个房间的垂向振动加速度1/3 倍频程谱曲线。

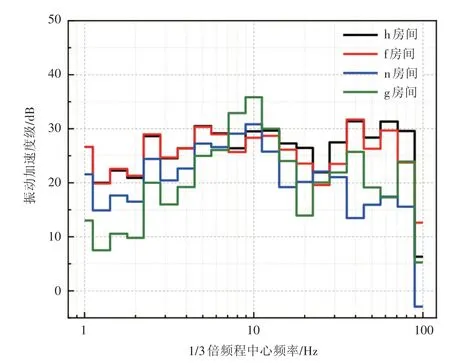
图8 6层各房间的垂向振动加速度1/3倍频程谱曲线

从图8 可以看出，同一楼层中，受房间与线路的距离、房间大小等因素的影响，不同房间内的楼板振动存在较大差异，最大分频振级差可达15 dB。故在对敏感点作减振设计时，必须更加具有针对性。同时，每个房间都出现多个振动峰值，10 Hz 附近峰值对应浮置板轨道的固有频率，30～50 Hz内峰值对应建筑物的典型固有模态频率，63 Hz 附近峰值对应轮轨系统耦合振动频率。

最后，经处理得到各楼层h,f,n,g 等4 个房间的垂向振动加速度1/3 倍频程谱曲线，如图9所示。

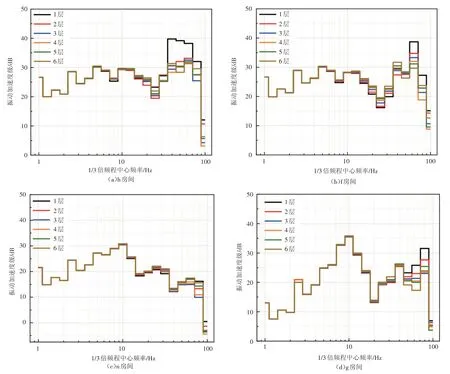
图9 不同楼层中各房间的垂向振动加速度1/3倍频程谱曲线

由图9 可以看出，各楼层中每个房间均较为明显地出现了4 个振动峰值，并且随着楼层的增高，同一房间的振动响应基本呈低频段振动衰减较慢或基本不衰减、高频振动逐渐衰减或先衰减后增大的特点。对不同楼层的房间而言，振动水平同时受楼层结构约束条件、与线路的距离等因素的影响，且不同房间内高频振动的衰减规律不尽相同。但总体而言，1 层直接受到地层传来的振动波的影响，因此振动最大；顶层由于约束较小，故振动也处于较高水平；中间楼层的振动最小。由此可知，振动在建筑物内沿垂向传播基本呈先减小后增大的特点。

3 结论

本文以某运营地铁浮置板轨道线路为背景，建立了地铁列车-浮置板轨道频域耦合解析模型及道床-隧道-地层-建筑物有限元仿真模型，对线路沿线某6 层砖混结构建筑物内的振动响应及振动在该建筑物内的传播规律进行了计算分析，主要得出如下结论。

1）典型浮置板轨道线路的沿线建筑物内，振动呈多频率峰值分布，这包含了浮置板轨道固有频率、建筑物自身固有模态频率以及轮轨共振频率的影响。其中，浮置板轨道能够有效控制高频振动但一定程度上放大了低频振动的特点在近场建筑物内仍有体现。

2）受边界条件、与线路的距离等因素的影响，同一楼层内不同房间的振动加速度响应具有显著差异，分频振级最大差值可达15 dB 以上。在纵向，案例中6 层建筑物内振动响应随楼层的变化基本呈先减小后增大的特点，底层楼板振动响应最大，顶层次之，中间楼层振动响应最小。因此，进行减隔振设计时，需要根据保护对象所在建筑物内的具体楼层及位置进行针对性的减隔振措施设计。

3）在对建筑物内敏感点进行振动控制时，必须提高减振措施设计的频率匹配意识，明确被保护对象的超限频段，这样可提升减振措施的针对性和有效性，避免减隔振措施的粗放使用。