基于交通参与者延误分析的环形交叉口行人过街信号设置条件

裴玉龙，徐亚融

（东北林业大学 土木与交通学院，黑龙江 哈尔滨 150040）

0 引言

在常规无信号环形交叉口中，人行横道处存在人车相互避让、减速让行等交互行为。人车交互行为不仅会增加行人和机动车的通行延误，还会威胁道路交通安全，甚至在避让失效时发生人车交通事故，造成人员伤亡和财产损失[1]。为保障行人在无信号交叉口的安全，我国《道路交通安全法》[2]修订后规定：“机动车行经没有交通信号的道路时，遇行人横过道路，应当避让。”经实地调研发现，无信号环形交叉口处部分机动车驾驶员不遵守避让规则、与行人争夺通行权的现象时有发生，同时机动车频繁礼让行人也降低了交叉口通行效率。为优化人车交互问题，设置行人过街信号是方法之一，我国《道路交通信号灯设置与安装规范》（GB 14886—2016）[3]中对于兼顾行人与机动车、效率与安全的综合条件规定较模糊，缺乏相应的理论支撑和量化标准。因此，同时考虑环形交叉口的安全性与运行效率，定量分析行人过街信号的设置条件具有重要意义。

对于环形交叉口的信号设置，国内外学者主要从效率、环境和安全3 方面评估环形交叉口交通运行效果，分析其信号控制方案的合理性，通过建立微观交通模型和仿真模型明确信号设置标准。在效率评价方面，杨晓光等[4]在美国《道路通行能力手册（2000）》（Highway Capacity Manual,HCM2000）的基础上改进环形交叉口车均延误模型，基于车均延误计算最佳信号周期。此后马新露等[5]、马庚华等[6]针对环形交叉口车流特性提出延误模型，以交叉口延误时间为目标优化环形交叉口信号配时。刘仲波等[7]采集环道车流车头时距相关数据，利用模糊C-均值聚类算法判别环形交叉口交通拥堵程度，确定信号控制时段。Bassani等[8]开发了环形交叉口专用的视频图像分析系统，通过跟踪车辆轨迹分析环形交叉口运行效果。还有学者通过通行能力[9-10]、排队长度[11]和延误[12-13]等指标分析不同控制方法对环形交叉口运行效率的影响，为环形交叉口控制信号的设置提供参考。在环境评价方面，杨庆芳等[14]利用交通流参数构建了环形交叉口污染物排放量及燃油消耗量计算模型；Lakouari 等[15]探究了环形交叉口信号参数对一氧化碳排放量的影响。在安全评价方面，Karwand 等[16]使用视频数据监测环形交叉口潜在的人车交互行为，发现行人在有安全岛的环形交叉口出行安全性更高。频发的人车交互行为不仅会降低行人的安全性，还会干扰交通流的连续性，影响交通效率。因此，学者们分析了人车交互行为对交通的影响，结果表明行人、机动车和环境等因素均会影响人车交互行为，进而影响交叉口交通模型（包括通行能力计算模型、延误计算模型等）[17-18]。在环形交叉口人车交互行为分析方面，Li 等[19]使用元胞自动机模型分析了双车道环形交叉口人车交互行为对交通安全和效率的影响；Layegh 等[20]通过考虑过街行人的行为模式探究多车道环形交叉口可能发生人车交互的时间和空间。

综上，在环形交叉口信号控制研究方面，现有成果主要以机动车运行指标（如延误、通行能力）为优化目标，忽略了实际人车混行交通环境中行人的利益，并且此前关于人车交互行为的研究大多针对十字交叉口，较少深入考虑环形交叉口处人车交互因素，使得模型在不同交叉口的应用存在一定的误差。基于此，本文结合我国道路交通机动车礼让行人的实际情况，引入机动车让行率，构建不同人车交互环境下环形交叉口交通参与者延误模型，从通行效率角度提出适用于我国不同城市、不同环形交叉口的行人过街信号设置条件，并通过数值仿真模型与微观交通仿真模型，分析不同环境下设置行人过街信号的灵敏度及应用效果。以期为环形交叉口行人过街信号的设置提供理论依据。

1 问题描述与调查方案设计

1.1 问题描述

无信号环形交叉口交通流运行复杂，人行横道处存在大量人车交互行为，行人路权难以得到保障，为解决上述问题可通过在环形交叉口设置行人过街信号，对行人与机动车相互干扰的问题进行优化。环形交叉口行人过街信号同时考虑了行人和机动车的通行权，其相位设置如下：第1相位为东西向行人相位，此时东西方向机动车直行、左转、右转；第2 相位为南北向行人相位，此时南北方向机动车直行、左转、右转；第3 相位为机动车专用相位。设置行人过街信号后，各相位中环形交叉口机动车及行人交通运行组织如图1所示。

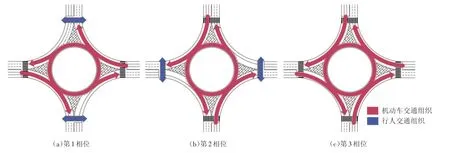
图1 交通流运行组织

在南北走向和东西走向的人行横道处设置行人过街信号，信号中最短绿灯时间应满足行人过街所需的最短时间，并且可以等待行人消散完成，周期时长应允许等待车辆能行驶至环道。在交通量大的情况下，为避免车辆因等待空间不足产生排队现象进而导致较大延误，影响车辆运行，应从交叉口处交通参与者通行效率角度，根据环形交叉口的人车交互情况和交通量特征，分析设置行人过街信号的合理性。

1.2 数据采集与整理

为分析无信号环形交叉口交通特性与人车交互行为特征，选取哈尔滨市两个无信号环形交叉口开展视频数据采集工作。交叉口1为博物馆环形交叉口，交叉口2为迎宾路-腾达大街环形交叉口，其基本信息如表1所示。此次调查选择天气状况良好的工作日，数据采集时段为11:00—13:00 和16:00—18:00。所调查的两个环形交叉口机动车均以小客车为主，大型车占比较低，分别为5.4%和4.1%。

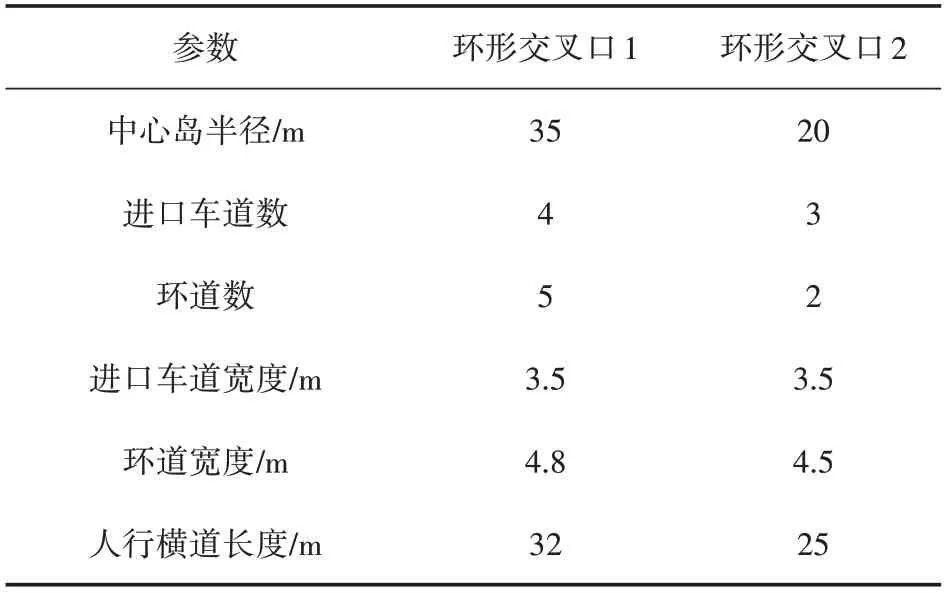
表1 环形交叉口基本信息表

行人过街速度是行人交通设施设计、服务水平评价等的重要参考指标。本文采用Corel VideoStudio 软件对所收集的视频进行数据提取，其精度为25 帧/s，提取时间数据精度为0.04 s。根据提取的无信号环形交叉口行人过街速度数据，两个环形交叉口行人过街速度分布如图2所示。

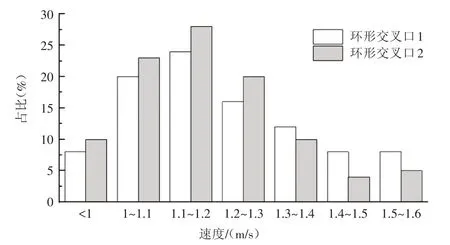
图2 行人过街速度分布图

机动车到达交叉口的分布假设是计算交叉口车流延误时重要的输入参数，根据假设分布规律建立的延误模型都有适用条件的限制，交叉口车辆具体到达分布需要根据实际车流情况数据进行拟合，为方便计算延误，本文假设车辆到达符合泊松分布。另外，根据环形交叉口1 北进口直行方向车辆到达情况拟合车头时距分布，结合已有的车头时距分布模型[21]，采用对数正态分布、逆高斯分布和负指数分布对数据进行初步拟合，车头时距分布拟合结果如图3 所示。根据极大似然估计法得到各分布函数的参数，具体结果如表2所示。通过K-S检验法测试3种模型，结果显示3种模型都通过检验，本文假设车头时距服从负指数分布。

表2 车头时距分布参数的极大似然估计

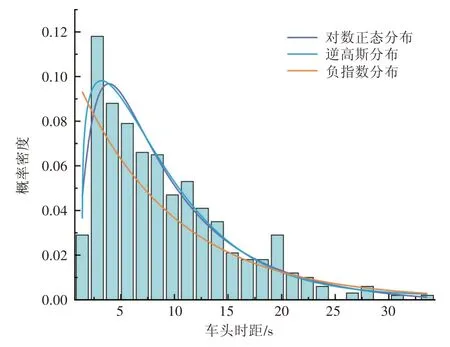
图3 车头时距分布拟合图

1.3 人车交互行为特征分析

无信号环形交叉口人行横道处机动车和行人的通行过程，是一个人车相互干扰的过程，人车交互示意图如图4 所示。选取无信号环形交叉口1 509 辆机动车让行行人的行为数据进行抽样调查，发现实际交叉口处人车交互行为具有多样性，参考Haperen 等人的相关研究[22]及环形交叉口人车运行特性，按照以下原则对人车交互行为进行分析：①机动车因行人穿越而变换车道、减速和停车均计为人车交互；②过街行人因担心与通行机动车碰撞而减速、停止前进和后退均计为人车交互；③1 名行人与同向不同车道上机动车分别发生交互行为时，将其定义为多次人车交互；④一辆机动车与多名过街行人在同一车道发生交互行为，计为1次人车交互。

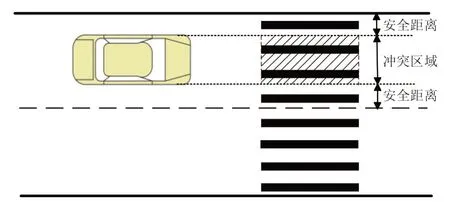
图4 人车交互示意图

本研究抽样调查统计数据显示，83.89%的机动车在冲突区域前礼让行人，16.11%的机动车在行人位于冲突区域内时不礼让行人。机动车礼让行为可归结为减速让行和停车让行，在礼让行人的机动车中，减速让行的机动车占比为81.55%，停车让行的机动车占比为18.45%，具体数据如表3所示。

表3 机动车让行特征统计表

2 交通参与者总延误估计模型

2.1 机动车让行率

人车发生交互时必定会有一方避让另一方，不同的避让方式和避让对象会影响延误的大小，基于此原因及前述人车交互原则，引入机动车让行率这一变量，用于计算交通参与者总延误。

将机动车让行率定义为行人与机动车交互总次数中，机动车避让行人的次数所占比例。因此机动车让行率k的计算公式为：

式（1）中：Ncp为人车交互总次数，单位次；M为机动车避让行人行为次数，单位次。

2.2 模型假设条件

为简化问题并突出关键，对模型做出如下假设：

1）环形交叉口交通负荷程度没有达到饱和或过饱和；

2）假设机动车和行人的到达均符合泊松分布，且行人在交叉口过街时遵守交通信号控制方案。

2.3 行人过街信号设置前的延误分析

行人过街信号设置前的机动车延误包括几何延误和交通延误。其中几何延误是由环形交叉口几何形状所引起的车辆加减速和转弯延误。不同直径环形交叉口几何延误[23]不同，具体如表4所示。

表4 不同直径环形交叉口的几何延误

交通延误是由进口道行人干扰引起的机动车额外通行时间。在无信号控制的人行横道处，由人车交互行为引起的机动车延误Dv1计算公式为：

式（2）中：Lm为机动车减速距离，单位m；v0为车辆初始速度，单位m/s；am为机动车让行的减速度，单位m/s2。

在无信号交叉口的人行横道处，人行横道上没有行人的情况下，机动车也会减速观察后再通过，由此造成的机动车减速观察延误Dv2计算公式为：

式（3）中：an为机动车减速观察的减速度，单位m/s2。

行人安全穿越无信号控制的环形交叉口人行横道所需临界穿越间隙τp计算公式为：

式（4）中：n为单向机动车道条数；D为一条机动车道的宽度，单位m；vp为行人过街速度，单位m/s；tR为行人观察机动车运行情况、判断车间安全间隙的时间，单位s；t1为车身通过所需的时间，单位s。

当车头时距服从负指数分布时，行人穿越第j条机动车道承受的延误Ej计算公式为[24]：

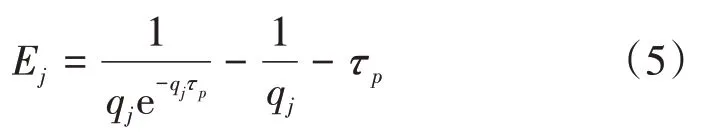
式（5）中：qj为j进口道机动车到达率，单位veh/s。

综上可得，行人过街信号设置前，环形交叉口交通参与者总延误Tdelay1计算公式为：

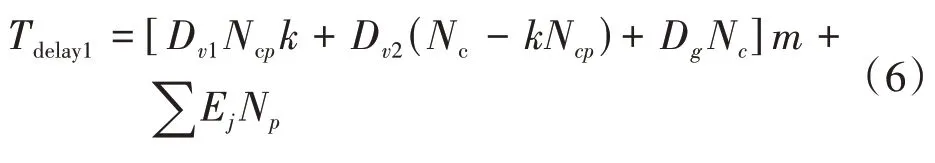
式（6）中：Dg为几何延误，单位s；Nc为机动车流量，单位veh/h；m为机动车平均载客数，单位人；NP为行人流量，单位ped/h。

2.4 行人过街信号设置后的延误分析

设置行人过街信号后，行人延误为信号控制带来的控制延误，采用Webster 延误公式计算行人延误：

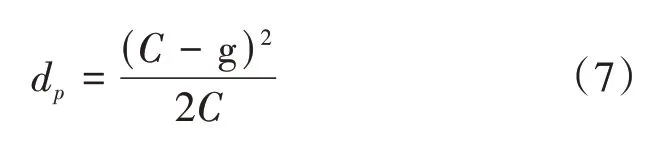
式（7）中：dp为行人延误，单位s；C为信号周期长度，单位s；g为行人过街信号有效绿灯时间，单位s。

设置行人过街信号后，为保障行人安全和通行路权，机动车必须在安全距离内为人行横道上过街行人让行。在信号灯绿灯时间内，机动车和过街行人的交互分为2 个阶段。第1 阶段：在绿灯初始阶段时，信号红灯时段内积累的等待行人连续穿越冲突区域，此时到达人行横道的机动车需要停车等待；第2 阶段：冲突区域中连续穿越的行人消散，此后行人随机到达冲突区域，若存在可穿越的行人到达间隔，机动车将直接穿越冲突区域，否则将停车等待。

根据绿灯期间行人和机动车相互干扰的2 个阶段，将在此期间的机动车延误计算也分为2 个阶段。

在第1 阶段，随信号绿灯亮起，等待区累积的行人开始消散，行人排队长度逐步减小，当队伍长度减小到零则完成行人疏散过程，用tb表示行人疏散时间，其计算公式为：

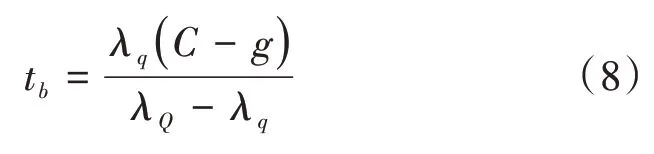
式（8）中：λQ为行人离开的饱和流率，单位ped/s；λq为行人到达率，单位ped/s。

行人从到达冲突区域边界到穿越冲突区域花费的时间tc计算公式为：

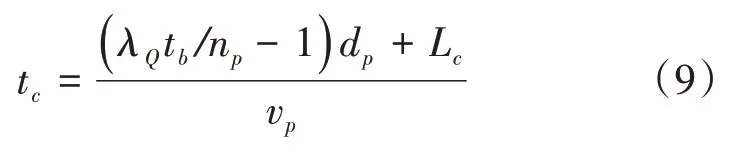
式（9）中：np为饱和流率下每排行人的数量，单位ped；dp为相邻两排行人之间的平均间隔，单位m；Lc为人车冲突区域长度，单位m。

在第1 阶段，机动车需要在行人群消散之前停车等待。此阶段的机动车延误包括等待过街行人群消散的时间及停车过程中产生的加减速延误。机动车停车等待过程中产生的加减速延误t1计算公式为：

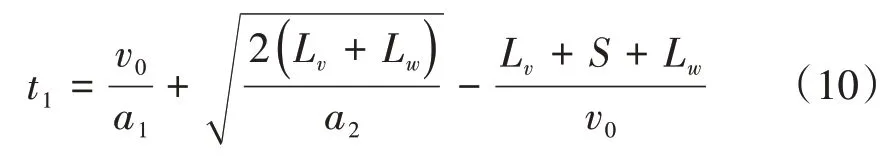
式（10）中：a1为停车等待加速度，单位m/s2；a2为加速离开加速度，单位m/s2；Lv为车身长度，单位m；Lw为人行横道宽度，单位m；S为机动车减速停车的距离，单位m。

根据定积分中值定理，机动车的等待延误t2计算公式为：

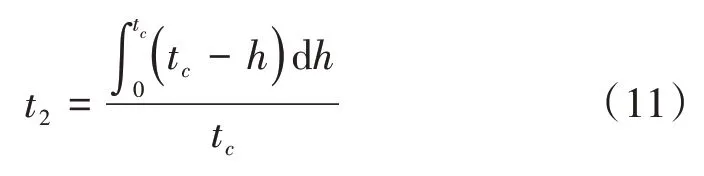
式（11）中：h为机动车车头时距，单位s/veh。

在第2 阶段，当等待区累积的行人穿越冲突区域后，机动车将在存在可穿越的过街行人间隙通行。若存在可穿越间隙，机动车直接穿越，若没有则需要停车等待。此时机动车需要穿越的距离为冲突区域长度Lc和车身长度Lv，设冲突区域宽度为Lct，则机动车穿越行人所需的临界穿越间隙τv计算公式为[25]：

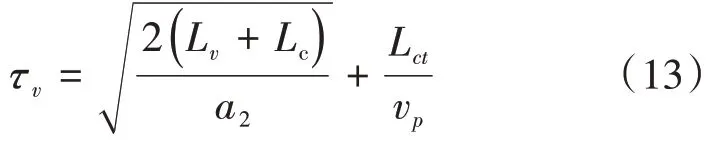
设前后行人到达时间间距为h1，机动车直接穿越的概率为P(h1＞τv)。

根据连续型随机变量总体均值的定义E(x)=假设有n个间隔，则机动车在冲突区域前等待行人的平均时间可以用等待小于可穿越间隔的平均时间表示。因此机动车等待行人的平均时间ht计算公式为：

则此阶段内到达的机动车延误总时间d2计算公式为：

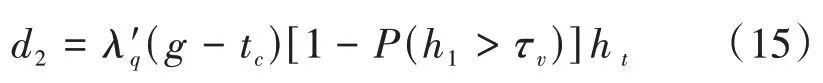
在行人过街信号红灯期间，假设行人遵守交通信号规则，在红灯时不会发生人车交互行为，则机动车在此期间时的延误d3为经过人行横道时减速观察产生的延误，其计算公式为：

由此可得，设置行人过街信号后，环形交叉口交通参与者总延误Tdelay2计算公式为：

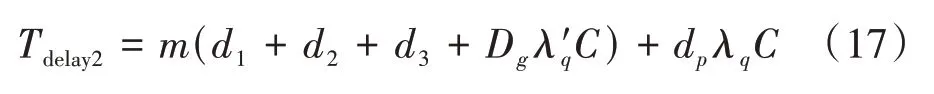
3 行人过街信号设置条件

基于交通参与者总延误指标，从道路通行效率角度提出行人过街信号设置条件，将机动车流量和过街行人流量作为设置行人信号的研究变量，提出交通参与者总延误最小的行人信号设置条件如下：

3.1 人车交互次数回归分析

为预测不同环形交叉口人车交互行为次数，以机动车流量、行人流量为变量指标，通过回归分析法建立人车交互次数预测模型。

基于视频采集的哈尔滨市博物馆环形交叉口红军街北进口和东大直街进口人车交互行为样本，按照人车交互分析原则对交互行为数据进行判别。实验观测数据以5 min为1个单位，记录在5 min内通过人行横道的机动车流量、行人流量和人车交互次数，机动车交通量中小型车、中型车、大型车的折算系数为1∶1.5∶2，行人交通量为双向过街行人数的总和。应用RStudio 软件建立人车交互次数与人流量、机动车流量的线性回归模型，得到的模型基本表达式为：

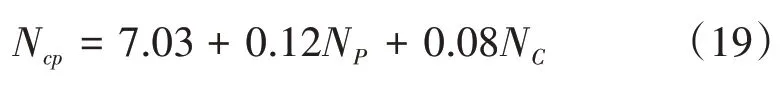
经检验，模型调整后的拟合优度R2为0.846，表明建模的数据可较准确预测人车交互次数。对模型总体进行F 检验，检验结果见表5，F值为108.1，显著程度参数Sig.为0，表明线性模型可较好描述人车交互规律。对参数进行T 检验，检验结果见表6，常数项的显著参数为0.056，机动车流量的显著参数为0.039，人流量的显著参数为0，表明用行人流量、机动车流量和常数项表述人车交互次数较理想。

表5 模型总体F检验表

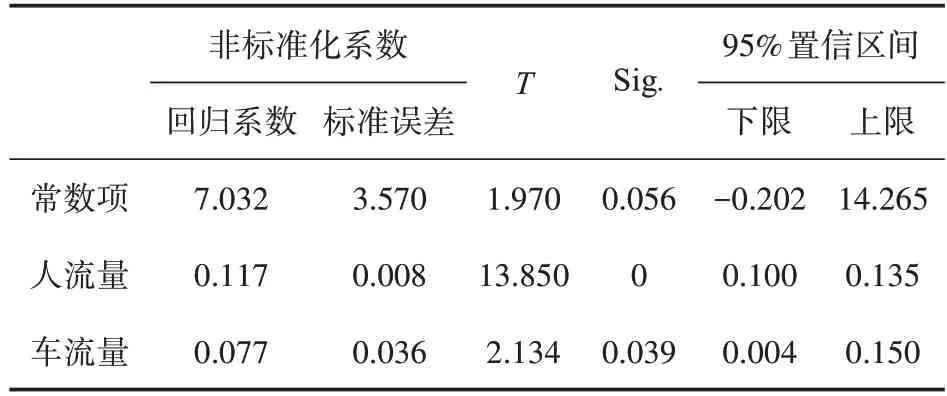
表6 模型参数T检验表

3.2 总延误增量灵敏度分析

通过Matlab 建模分析延误模型中各变量灵敏度，确定行人过街信号交通组织方法的适用条件。具体仿真环境设定如下：以半径为35 m 的4路环形交叉口为例，进口道和出口道各有4 条车道，车道宽度为3.5 m；共设置有3 条环道，环道宽度为4 m，环形交叉口内车辆运行速度设为30 km/h。

此次数值分析探究在不同机动车让行率场景中，不同机动车和行人流量条件下设置行人过街信号后总延误增量的变化情况。在HCM2000 中，现场调查了一系列不同交叉口的让行情况，结果显示机动车让行率在0.47～0.90[26]。为使模型能更满足真实情况，在数值分析中假设了驾驶员的最坏行为（机动车让行率1%）和最好行为（机动车让行率99%），结合HCM2000 中的记录结果，又设置了机动车让行率30%、机动车让行率50%和机动车让行率70%三种情况，数值仿真结果如图5 所示。

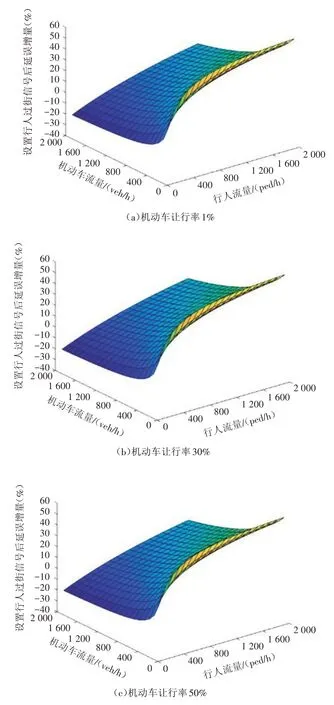
图5 不同让行率下总延误增量灵敏度分析

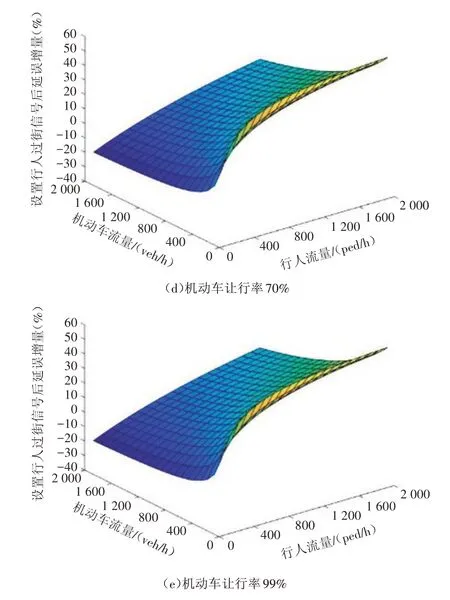
图5 （续）

通过总延误增量灵敏度分析可得出以下结论。

1）交通参与者延误随着交通量的增加而增加。原因是机动车流量的增长，导致车头时距大于可穿越间隙的概率降低，从而增加交通参与者的等待间隔数和等待时间。

2）在低机动车流量情况下，人车交互引起的避让延误及设置行人过街信号后带来的安全效益提升无法抵消运行效率的损失。随着机动车流量增加，设置行人过街信号后的总延误减小，因此此时更适宜设置行人信号。

3）同一机动车让行率下，机动车流量较大时，随着行人流量的增加，交通参与者总延误增长缓慢；机动车流量较小时，随着行人流量的增加，交通参与者总延误增长迅速。由此可知，总延误增量的增长速度在低机动车流量区域更加敏感。因此，在机动车流量较小且行人流量较大时，设置行人过街信号后总延误增加，此时不再适宜设置行人过街信号。

4）大部分情况下，当机动车流量达到660 veh/h 以上，且双向过街行人流量在380 ped/h以下时，适宜设置行人过街信号。在相同交通量场景下，随着机动车让行率的增加，设置行人信号后的交通参与者总延误更小，说明让行率对总延误增量有较大影响，有必要将机动车让行率作为模型输入条件。因为机动车让行导致避让延误增大，并且避让延误增速大于行人受到的干扰延误增速，此时在环形交叉口设置行人过街信号可提高运行效率和组织秩序。

4 案例验证

4.1 数据提取

上文以4 车道环形交叉口为例，通过数值分析探究了行人过街信号设置对环形交叉口运行效率的影响。使用相同的原理，该方法可以应用于其他车道数的环形交叉口，为证明该方法的普适性[27]，选取3 车道环形交叉口作为案例进行验证。以哈尔滨市双城区迎宾路-腾达大街环形交叉口为平台开展数据采集工作，其中迎宾路为南北走向，腾达大街为东西走向，该4 路环形交叉口直径为40 m，进口车道宽度为3.5 m，环道宽度为4.5 m，环形交叉口几何构型如图6所示。

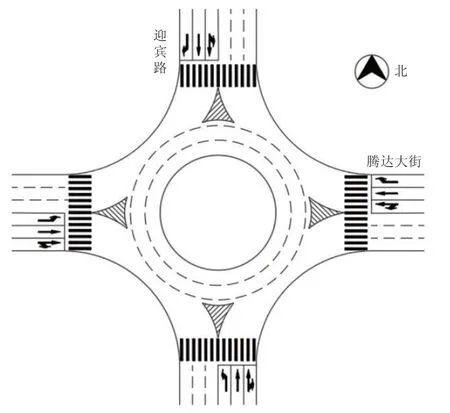
图6 环形交叉口示意图

调查交叉口腾达大街东进口方向车辆和过街行人延误。采用牌照法[28]调查机动车延误，取置信度为90%，需要的最小样本数为：

式（20）中：St为引道时间标准差；K为置信度90%下的K值；Et为引道时间容许误差。

横跨腾达大街的间距约为25 m，取行人过街平均步速为1.2 m/s，则行人过街信号的最短绿灯时间为22 s。对该环形交叉口进行实测，其中过街行人和机动车到达率取多次采样数据的平均值。采集车辆延误数据时，每次观测采样数都要达到式（20）要求的最小样本数，按照牌照法的要求处理观测数据。对腾达大街进口方向进行现场实测，交通量检测数据见表7。机动车交通量组成主要包括小客车和大客车，观测期间通过交叉口的小客车平均每辆车承载2.1 名乘客，大客车平均每辆车承载13.3名乘客。

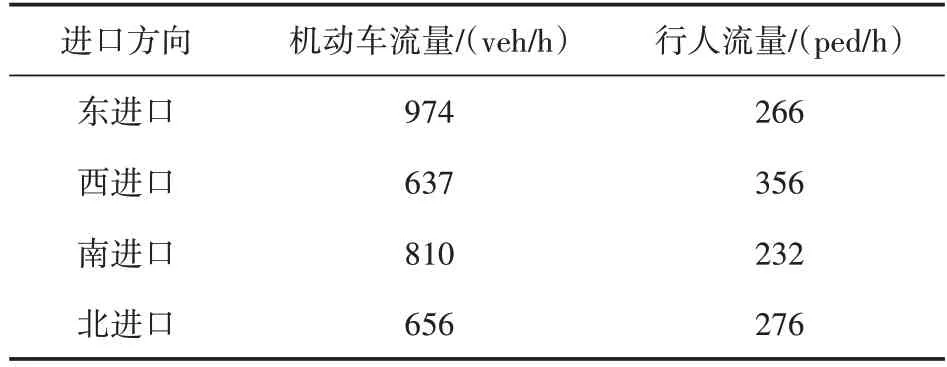
表7 各进口方向交通量实测结果

4.2 仿真对比

根据腾达大街-迎宾路环形交叉口的几何特征及其交通量组成，采用设置行人过街信号的交通组织方法，利用Vissim 软件对该路口进行模拟仿真，对比行人过街信号设置前后交通参与者总延误等指标，具体结果见表8。

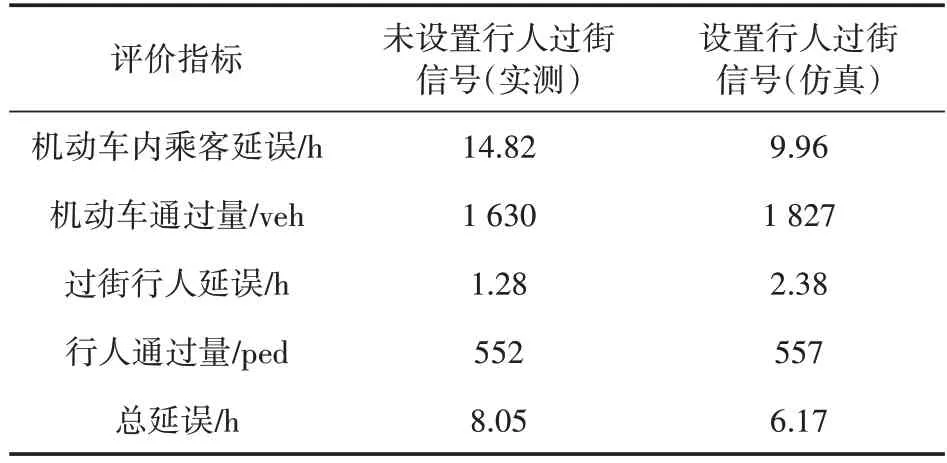
表8 实测指标与仿真指标对比

由表8 可看出，与未设置行人过街信号的实测数据相比，设置行人过街信号后，机动车通过量和行人通过量增加，机动车内乘客延误减少，过街行人延误增加，交通参与者总延误降低了23.3%，与灵敏度分析得到的结论一致，表明在此环形交叉口设置行人过街信号是合理的。

5 结束语

本文对环形交叉口处人车交互行为进行了分析，综合考虑环形交叉口中所有交通参与者的通行效益，以总延误为优化指标消除了不同交通方式之间载客率的差异，从通行效率角度提出环形交叉口行人过街信号设置条件，基于环形交叉口的人车交互行为视频标定模型参数，通过数值分析和交通仿真对模型参数所给适用范围的准确性和有效性进行验证。分析结果表明，行人流量不变时，机动车流量越高设置行人过街信号效果越好，且机动车让行率会影响行人过街信号设置效果，因此有必要将让行率纳入行人过街信号设置的输入条件。但是，本文仅以交通参与者总延误为优化指标，并未综合考虑环形交叉口通行能力和环境效益。鉴于我国城市交通的混合交通特性，未来可基于环形交叉口人车交互视频数据，进一步探讨行人过街信号的参数设置问题。