基于纳什协商的电力交易策略研究

张志翔, 罗文海

(广州电力交易中心有限责任公司, 广东, 广州 510663)

0 引言

随着物联网以及城市发展的逐步扩大[1-3],电力的需求和供电的要求[4-5]也越来越高。

常见的P2P电力交易面临多重安全和隐私威胁。一方面,如果电力市场不完全可信和透明,则P2P网络节点进行大规模分布式交易是不安全的。另一方面,由于担心安全性和违约问题,电力过剩的节点可能不愿意参与交易。在这种情况下,节点之间的电力供需将存在失衡现象。

此外,区块链技术[6]可为电力市场的运营模式、拓扑结构和安全性注入新活力。作为一个分布式数据库和分散的P2P网络,区块链具有智能合约、分布式决策、协作自治、高防篡改安全性和透明性的特点[7]。与传统的集中式电力市场不同,P2P平台不需要存储可再生能源并预测所有参与者的负荷需求,从而避免了隐私和安全问题。然而,市场参与者之间存在利益冲突,需要考虑交易公平性问题。

为了改善P2P电力交易公平性问题,本文基于纳什协商(NBS)理论提出了分布式P2P电力交易模型。该模型可以最大化市场参与者的利益,从而使市场参与者获得Pareto最优收益。

1 分布式P2P电力交易模型

1.1 系统结构

图1为分布式P2P电力交易模型结构。其中,市场参与者包括负荷聚集商(LAs)和微电网运营商(MGO)。对于LAs,负载主要有固定负载、可中断负载和可移动负载;对于MGO,主要由储能系统(ESS)、可再生能源发电机、内部负载和通信设备组成。为简化计算,使用集合C={1,2,…,c}表示LAs,集合N={1,2,…,n}表示MGO。此外,模型的运行时间以d为单位,用集合T={1,2,…,t}表示,其中t=24 h。在该模型中,市场参与者不仅可以与配电网运营商(DNO)进行电力交易,还可以通过协商完成电力交易过程,同时DNO可以向参与者收取网络损失的运输成本。为此,基于NBS执行P2P交易,从而使市场参与者能够获得Pareto最优收益。

图1 分布式P2P电力交易模型结构

1.2 网络损耗分析

当LA与DNO、MGO进行交易时,电力交易中通常存在3种网络损耗。首先,通过配电网的电力传输损耗。其次,变压器损耗主要包括铜损耗和铁损耗;铜损耗指变压器一次绕组和二次绕组电阻引起的损耗,可通过短路试验获得;铁芯损耗指铁芯中交变磁通引起的损耗,通常认为等于空载损耗,可通过空载试验获得。最后,由其他因素造成的损耗,如由于获得可再生资源和新电气设备而导致日益严重的谐波损耗、电容器的介电损耗、电抗器损耗等(包括导体损耗、磁滞损耗、涡流损耗等)。一般来说,线路上的电流越大,其他因素造成的损耗就越大[8]。基于上述考虑,令MGO为n,LA为c,则电力交易过程中总损耗计算如下:

(1)

(2)

进一步,将式(2)代入式(1),网络总损耗更新为

(3)

当LA和MGO进行交易时,DNO可基于时隙t时的网络损失向其收取运输成本,则有:

(4)

其中,γ表示网络损耗惩罚系数。同时,运输成本由LA和MGO双方平等分担。

1.3 LA模型

在P2P电力交易模式下,每个LA可以与DNO和MGO进行独立交易。因此,∀c∈C,∀n∈N,LA的收益函数定义如下:

(5)

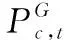
(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

1.4 MGO模型

对于任意MGO(∀n∈N),其可以与DNO、LAs和其他MGO进行交易。因此,∀n∈N的目标函数定义如下:

(15)

(16)

(17)

(18)

(19)

(20)

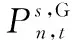
进一步,ESS的充电和放电状态应满足以下约束条件:

(21)

(22)

(23)

Sn,0=Sn,T,∀n∈N

(24)

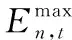
(25)

(26)

2 基于纳什协商的电力交易优化模型

2.1 P2P纳什协商模型

当DNO在时隙t处向第n个MGO或第c个LA购买/出售电力Pt时,第n个MGO或第c个LA的收入/成本在一天内计算如下:

(27)

进一步,假设第n个MGO或第c个LA达成协议,双方之间的付款满足:

(28)

综上,基于纳什协商的电力P2P公平交易模型描述如下:

s.t.式(6～14),式(16～28)

(29)

然而,式(29)为一个非凸问题,为此,将其分解为2个序列凸子问题:

s.t.式(6～14),式(16～26)

(30)

s.t.Zc≥0

(31)

2.2 基于改进ADMM的模型求解

考虑到集中式计算方法一方面使得交易参与者的隐私安全受到威胁,另一方面由于过度的数据处理,容易出现单点故障。为此,使用一种改进的交替方向乘子法(AD-MM)来解决电力协商问题。ADMM算法为一种典型分布式算法,然而LAs和MGO通过电力交易存在耦合行为,导致计算量大,收敛速度慢,故对其进行改进。

为了加快ADMM算法的收敛速度,首先对合作联盟中的所有参与者在第k个迭代由惩罚参数ρ进行约束:

(32)

其中,τin、τdec和μ表示常数参数,rk和sk表示原始残差和对偶残差,其为ADMM算法的收敛标准。

算法1基于改进ADMM算法求解Sp11:初始化k=0;拉格朗日乘子λn,ct,(0)=0,λn,n't,(0)=0;惩罚参数ρn,ct,(k),ρn,n't,(k);收敛精度ε12:while∑C+Nm=1rk1,m+∑C+Nm=1sk1,m 2>ε1 do3: k←k+14: 计算λn,ct,(k-1)和ρn,ct,(k-1)5: 根据式(30)计算^ρn,ct,(k-1)6: 根据式(31)计算ρn,ct,(k)和ρn,n't,(k)7: 更新λn,ct,(k),λn,n't,(k),ρn,ct,(k)8:end while

3 案例与分析

3.1 运行环境与参数设置

为了验证模型有效性,以某市2个LA和3个MGO之间分布式P2P电力交易为案例进行分析。实验时运行环境如下:硬件为酷睿i7 CPU,内存为64 G ARM的联想工作站;所有模型均运行在MATLAB 2019进行编译。

选取的配电网覆盖范围为12×12 km2。配电系统中LA1位于(0,3),LA1位于(9,6),MGO 1位于(0,9),MGO 2位于(12,6),MGO 3位于(6,3)(为简化计算,实验时将交易距离设定为参与者之间的地理直线距离,且位置单位均为km)。同时,LAs的每日预测负荷、负荷和MGO发电量均由电网公式提供。实验时相关参数设置如表1所示。表2为每小时分时电价。

表1 仿真过程中相关参数

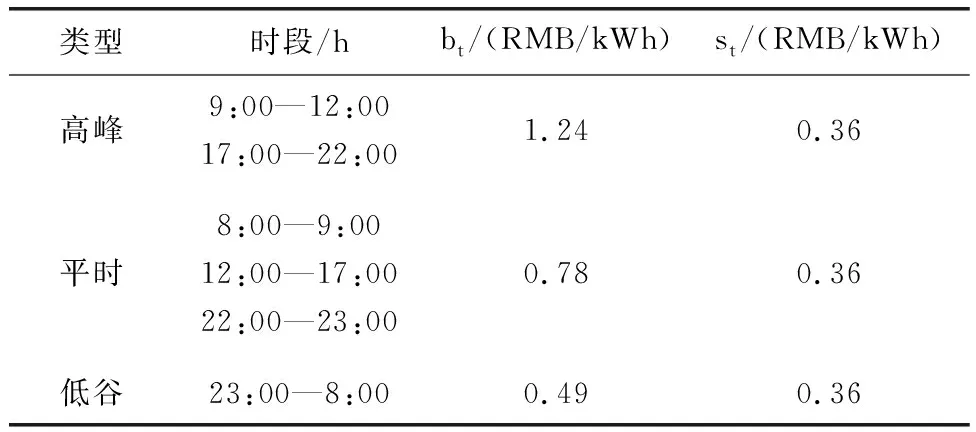
表2 每小时分时电价

3.2 仿真与分析

表3为分布式P2P电力交易模式下市场参与者的收益统计情况。其中,负值表示经纳什协商后向他人付款,正值表示收到付款。与传统模式下的收益相比,分布式P2P模型下参与者的收益有所提高,且每个参与者的剩余收益大体相同。根据本文所提模型,LAs和MGO可以获得公平交易,且具有Pareto最优收益解。

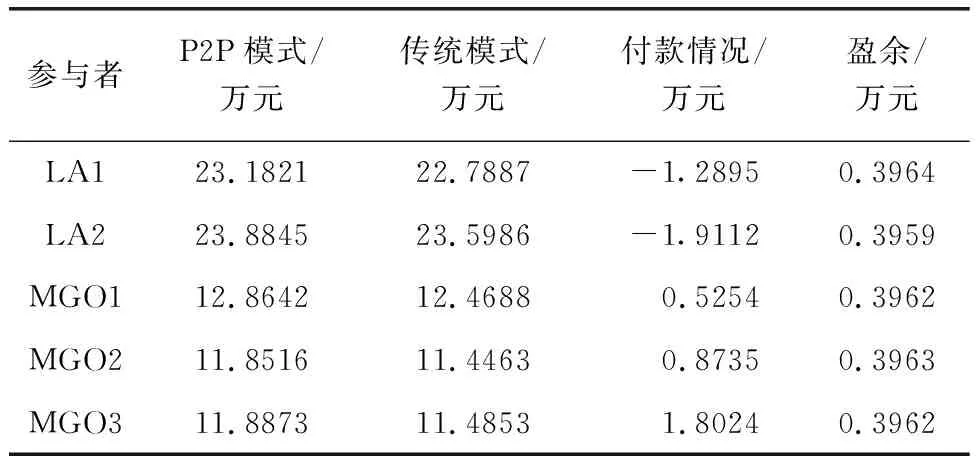
表3 市场参与者的收益

图2和图3为LAs和MGO经纳什协商后的负载变化曲线。由图2、图3可以看出,LAs和MGO在协商后的负荷曲线比通过最佳需求响应获得的原始曲线更平滑。对于用户而言,9:00-12:00和17:00-22:00期间的电力消耗是分时电价的高峰时段,因此将这些时段的负荷转移到平时段或低谷段可以有效地降低负荷功耗成本。此外,通过调峰填谷,MGO在分时电价高峰期间可以有更多的剩余电力。在电价高峰期间通过协商向消费者出售剩余电力可以提高其收益。

图2 LAs经纳什协商后的负载变化曲线

图3 MGO经纳什协商后的负载变化曲线

4 总结

本文基于区块链和纳什协商模型对电力交易策略进行了研究与分析,提出了一种分布式P2P电力交易模型。首先,基于纳什协商解执行P2P交易,从而使市场参与者能够获得Pareto最优收益。进一步,基于分布式P2P平台通过先进的信息和通信技术(如蜂窝通信)与所有市场参与者进行通信,同时可进行监督交易,为所有参与者提供清算服务,并更新分布式P2P交易过程中的相关变量,以确保电力市场的有序稳定运行。该模型为智能电网电力交易提供了借鉴。