直升机显模型跟踪解耦控制设计

王晓锋,赖水清

(1.中航技进出口有限责任公司,北京 100176;2.中国直升机设计研究所,江西 景德镇 333001)

0 引言

直升机作为控制对象,与固定翼飞机相比,具有更复杂的气动特性,四个控制通道(俯仰、横滚、航向、总距)间存在着强轴间耦合,尤其是在贴地飞行及悬停状态。俯仰与横滚交叉耦合,总距与俯仰,总距与航向之间的交叉耦合成为影响直升机飞行品质的主要因素。因此解耦设计已成为直升机控制界普遍关注的研究课题。目前直升机控制系统是否具有解耦功能已成为评价其先进性的主要指标之一,并列入了直升机主动控制技术研究范围。

国外从70年代开始不断研究直升机解耦控制技术。70年代中期,“黑鹰”直升机上率先采用具有解耦效果的汉密尔顿公司飞控系统。80年代中期,美国陆军与DFVLR共同制定了直升机显模型跟踪自适应解耦控制研究计划:将显模型设计成四通道线性理想解耦动力学模型,然后设计一个合适的控制律,使直升机强迫跟踪显模型,以达到解耦效果。地面仿真试验和飞行试验,验证了上述解耦方案可明显改善飞行性能与飞行品质,极大地减轻驾驶负担。该项技术已获得工程应用,如美国的RAH-66和欧直的NH-90直升机,都是采用显模型跟踪解耦控制技术设计飞行控制律[1]。

1 显模型跟踪解耦控制系统设计

1.1 系统设计的基本机理

显模型跟踪控制系统要求开发显模型跟踪的控制律,使控制对象在一个采样周期内强迫跟踪显模型,并具有优良的跟踪动特性与稳态性能。显模型为一电子模型,它体现了飞行员对飞行器的操纵特性要求。因此,改变模型特性即可以灵活地改变操纵特性的要求。对于直升机的俯仰、横滚、航向、总距四个通道,可根据飞行品质要求分别设计显模型。由于各通道直接跟踪各自的显模型,而其它通道处在镇定状态,因此显模型跟踪系统具有良好的解耦性能[2]。显模型跟踪控制系统的结构图如图1所示。

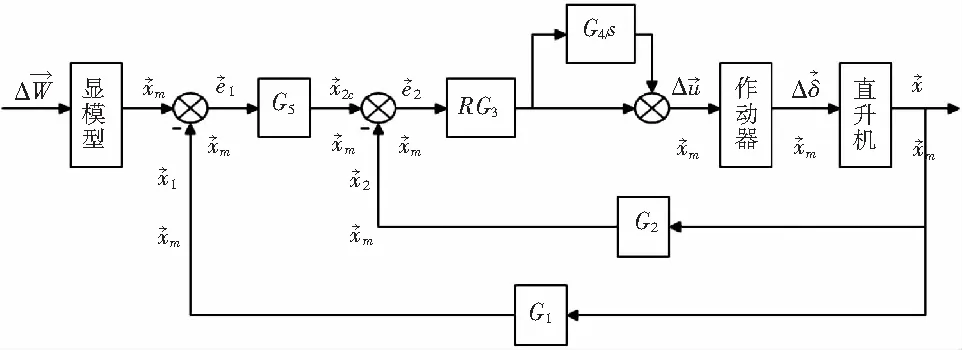
图1 显模型跟踪控制系统结构图

跟踪的动静态性能将取决于前向增益阵R和积分常数阵G4。其中,调节对角阵R的元素可以改善系统在一拍内跟踪的动态特性,调节对角阵G4的相应元素可以减少系统一拍跟踪的稳态误差。需要指出的是,四个作动器中任一个的速率或位置限制超出饱和值时,控制量与直升机实际输出量之间的误差会迅速建立起来,且由于饱和积分而导致系统不稳定。克服的办法是停止控制器输出信号的积分,哪个轴的作动器处于限制状态,就把G4阵的相应元素置零。

显模型跟踪控制系统具有良好的解耦性能,因为直升机的实际状态量分别跟踪相应的模型输出,而其他通道模型输出量为0,处在镇定状态。由操纵通道工作而耦合至镇定通道的耦合运动可视作“干扰”,而良好的镇定系统本身具有抑制耦合干扰的能力。这样,就从本质上减小了直升机的轴间耦合,极大地改善了直升机系统的解耦性能。

1.2 显模型的设计

显模型的设计可以充分体现模型跟踪控制系统设计的灵活性,可以根据不同的性能指标,采用不同的解耦显模型。常用的两种解耦显模型是一阶线性解耦模型和二阶线性解耦模型,用传递函数表示为:

其中:C为灵敏系数,T为时间常数,ξ为阻尼系数,ωn为带宽。

1.2.1 显模型带宽的选择

带宽的选择直接关系到显模型跟踪解耦性能的好坏。在一定范围内,系统的跟踪性能会随着带宽的增加而下降。这是因为直升机的响应速度较慢,本身带宽比较窄。如果显模型带宽过大,直升机响应速度将难于跟上显模型输出状态的变化。根据直升机模型的带宽,并结合ADS-33规范对各通道小幅度操纵输入的短周期响应的要求,设定各通道对应的带宽ωn。

1.2.2 灵敏系数C的确定

灵敏系数C的选择有两条准则:一种是在驾驶员操纵下获得良好的性能,这在很大程度上取决于经验和主观感觉;另一种定量的方法是利用ADS-33规范对直升机性能的要求来确定灵敏系数。

1.2.3 阻尼系数ξ的选取

根据ADS-33对系统阻尼的要求,结合工程经验,一般选取二阶线性解耦模型的阻尼系数ξ=0.7。

1.3 控制阵G3的设计

设计模型跟踪系统控制律的第一步是将自然直升机非线性动力学方程线性化,产生线性化运动方程:

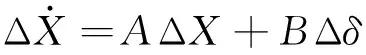
(1)

然后用后向差分法将上述方程离散化得:

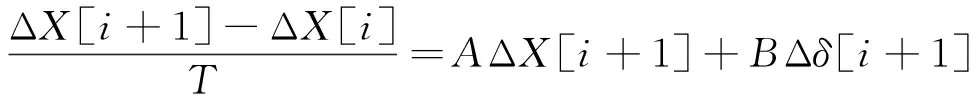
(2)

式中T是模型跟踪系统的采样时间,

式(2)可写为 :

ΔX[i+1]=[I-AT]-1ΔX[i]+

[I-AT]-1BTΔδ[i+1]

令

AD=[I-AT]-1,BD=[I-AT]-1BT

则

ΔX[i+1]=ADΔX[i]+BDΔδ[i+1]

(3)

因为上述线性运动方程是相对于配平状态的小扰动而进行线性化的,因此,式(3)的小扰动增量运动可写成:

X[i+1]-XT[i]=AD(X[i]-XT[i]+

BD(δ[i+1]-δT[i])

(4)

式中XT[i]为配平状态。

令Δδ=δ[i+1]-δT[i],表示四个作动器的当前拍位置相对于配平位置的变化。

假定系统能实现:经历一个采样周期后可使系统进入配平状态。这是本显模型跟踪控制系统设计中的一个极其重要的假设。

则X[i]=XT[i]

式(4)可写为:

X[i+1]=X[i]+BDΔδ

(5)

模型跟踪控制系统的目的应是使实际状态跟踪指令状态。最好的跟踪效果是实际输出X[i+1]和模型输出Xm[i]只相差一个采样周期,即一拍的时间延迟,也即,经一拍的采样周期T后,将直升机控制到所需的配平状态,因此:

X[i+1]=Xm[i]

(6)

将(6)式代入方程(5)得:

Xm[i]-X[i]=BDΔδ

(7)

可最终获得该系统的控制律:

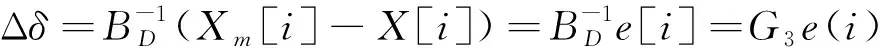
(8)

式中控制阵G3定义为自然直升机离散控制阵的逆:

2 系统参数优化

由于控制阵G3的设计只能够保证直升机一拍跟踪模型的输出,在这一拍时间内,系统跟踪的动态品质的好坏和稳态误差的大小取决于各参数矩阵;此外,显模型的带宽,采样周期的大小都对系统的跟踪性能有很大的影响,因此需进行参数优化[3]。

2.1 参数R的选取

由图1可知,控制阵G3前乘以一个R因子,用来改变系统内回路的前向增益,改善系统的动态跟踪性能,即保证每一拍内有良好的模型跟踪动态性能。R是一个对角阵,对角线上的元素对应各通道的增益大小。增益太小,解耦效果不好;增益过大,会引发振荡。设计过程中设定几个R值,在比较的基础上确定性能最优的R值。

2.2 G4阵的选取

矩阵G4对角线上各元素代表四个通道的积分常数,调节积分常数的大小可以改善一拍时间内跟踪的稳态误差。选取的原则和上面相似,即四个通道分别选取几组积分常数,对仿真结果加以比较,选取最合适的参数。

2.3 G1,G2,G5阵的选取

G1阵和G2阵是系统内回路与外回路的选择阵,通过G1选取姿态角作为系统外回路,通过G2选取姿态角速率作为内回路。

G5阵确定外回路俯仰通道和滚转通道的增益,增益太小,调节时间过长,增益太大,其它通道容易出现振荡。应根据ADS-33所规定的姿态响应要求,选取纵向通道和横向通道的外回路增益。

2.4 模型带宽选取

显模型跟踪的性能与模型的带宽选择有很大的关系,由于控制对象的带宽限制,选择模型带宽时,应考虑与控制对象带宽的匹配。显模型的频带过宽,将会导致直升机实际输出难以跟踪显模型输出。如果显模型的频带过窄,则调节时间过长,达不到要求。

2.5 采样周期的选取

控制信号变化快时,要求相应地减小采样周期。但控制律的设计是基于一拍跟踪的原理,要保证对象在一拍之内达到配平状态,如果采样周期过小,系统受直升机带宽的限制,则不能保证在一拍之内达到跟踪目的,必将引起系统发散。

3 设计应用

以一直升机为例,采用上述显模型跟踪法设计解耦控制律,并在Matlab6.0的Simulink工具箱环境下进行数字仿真。图2为仿真结构图。通过参数优化,得到的控制律最佳参数如下。

图2 显模型跟踪解耦控制律仿真结构图

最终仿真结果部分如图3-图6所示。按照GJB902B-2017《军用直升机飞行品质规范》进行飞行品质评定,结果满足ADS-33D等级1要求。

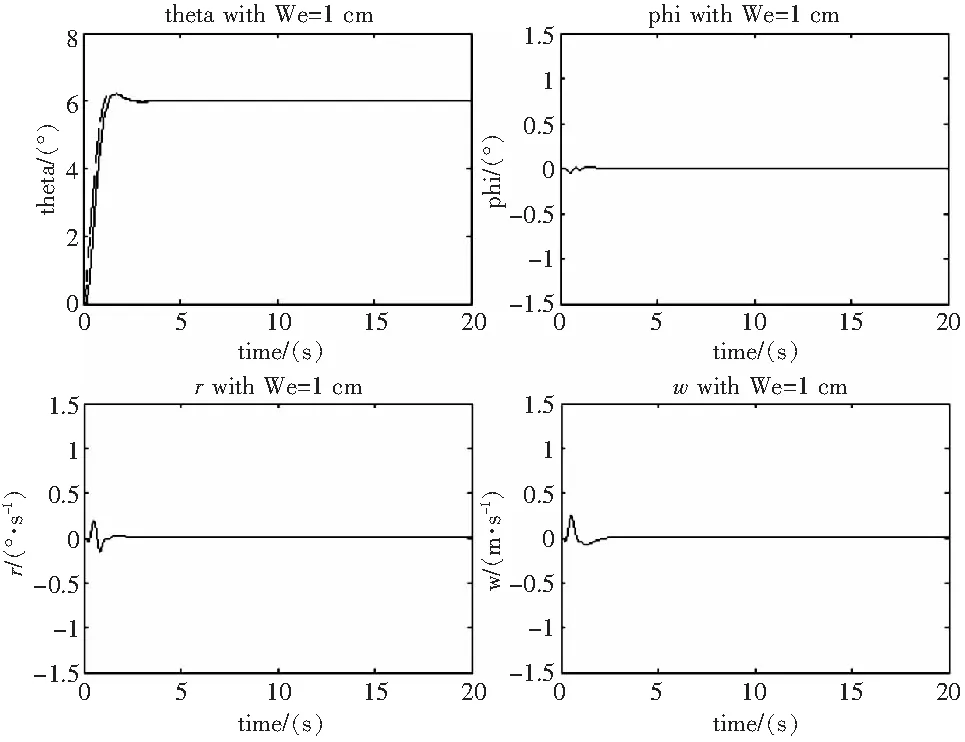
图3 纵向通道输入1 cm阶跃信号时各通道的响应曲线

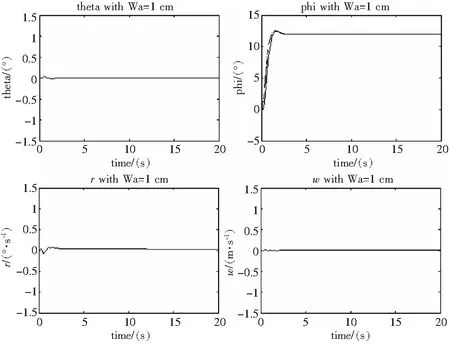
图4 横向通道输入1 cm阶跃信号时各通道的响应曲线

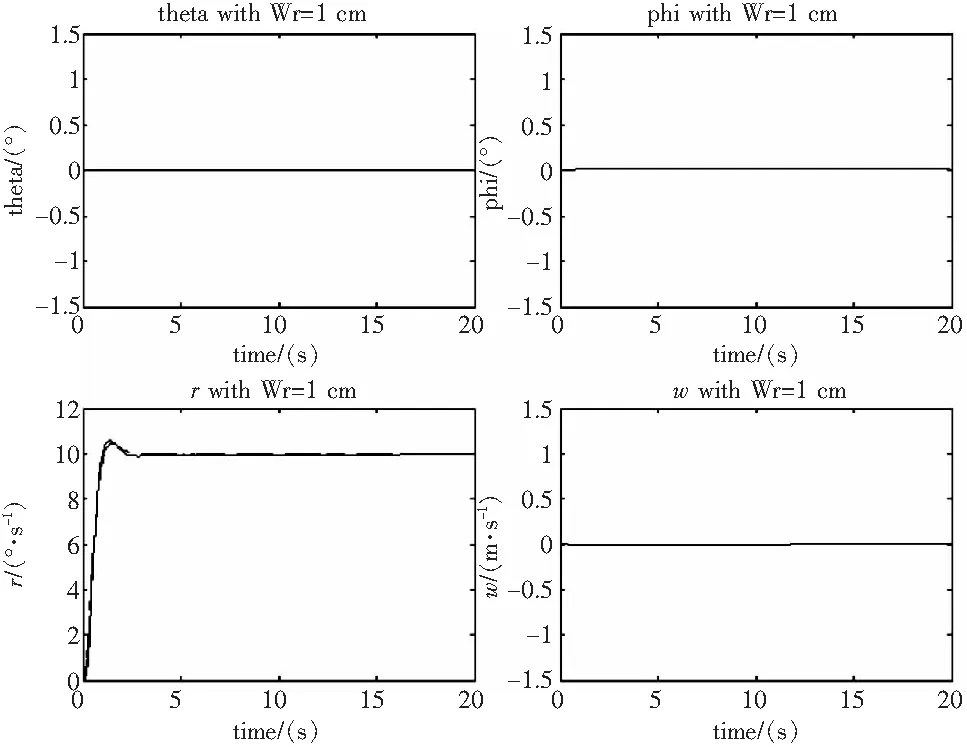
图5 航向通道输入1 cm阶跃信号时各通道的响应曲线

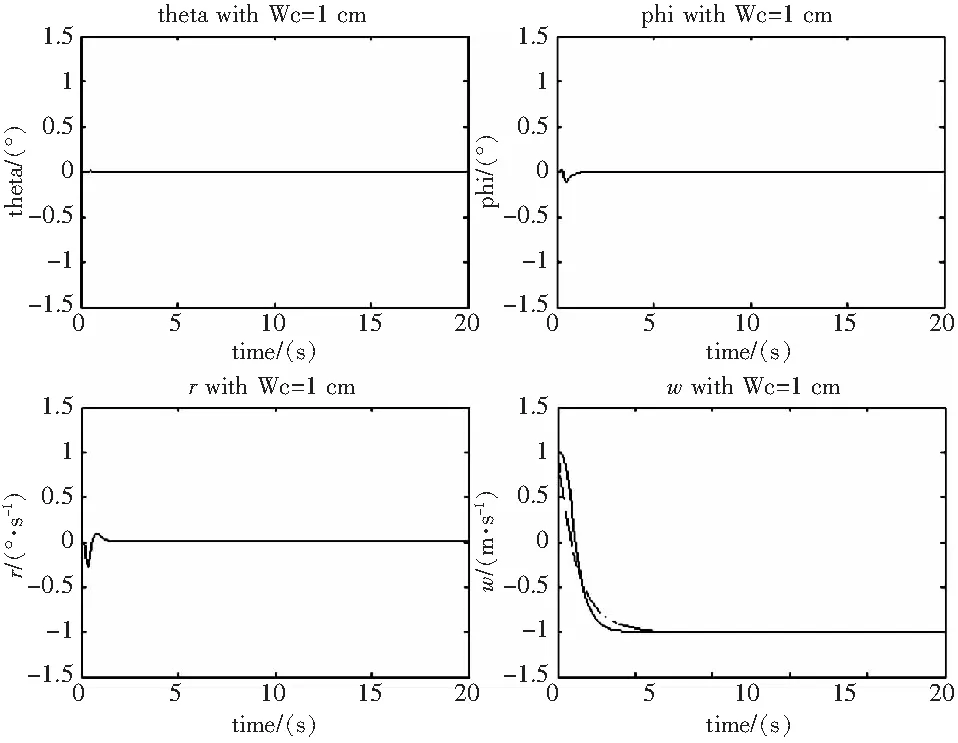
图6 总距通道输入1 cm阶跃信号时各通道的响应曲线

4 跟踪解耦性能评估

定量地研究模型跟踪解耦控制系统的设计性能,需要提出系统性能准则。以下对系统的跟踪与解耦性能分别进行讨论。

4.1 跟踪性能

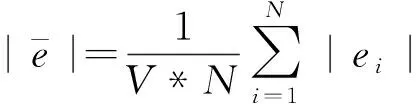
(9)

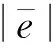
最后,模型跟踪性能定义为:

(10)

4.2 解耦性能

用类似的方法可以对每个轴的模型解耦性能进行统计测量。对同样的杆横向阶跃输入信号的俯仰轴的解耦性能可以定义为

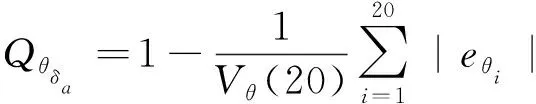
(11)

上面定义的性能指标将随显模型带宽的变化,系统的采样时间,测量时间N以及输入的阶跃信号值的大小而变化。因为仿真模型是线性的,故性能指标不随阶跃输入信号的大小而改变。

以直升机为例,设计的模型跟踪系统的各通道的Q值见表1(表中对角线上的数据表示四通道模型跟踪性能,其他元素表示各通道解耦性能)

表1 各通道跟踪性能与解耦性能评估表

从上表可以看出,模型跟踪系统使俯仰、横滚、偏航、总距四个通道都具有满意的跟踪与解耦效果。直升机的纵向运动与横向运动之间,轴与轴之间的耦合作用大大减少,既改善了系统的稳定性,又保证了良好的操纵性能。减小了驾驶员的工作强度,也降低了操纵的难度,从而起到了改善驾驶性能,提高控制精度的作用。

4.3 鲁棒性

为了验证系统的鲁棒性,我们仅考虑系统控制对象的建模误差,即控制阵不变,直升机的参数摄动。从仿真结果中可以看出,系统参数摄动,系统的跟踪解耦特性依然很好,表明显模型跟踪解耦控制系统具有良好的鲁棒性。

5 结论

控制律仿真表明:模型跟踪系统的解耦效果良好,跟踪性能好,具有良好的鲁棒性,能使飞行品质达到GJB902B-2017《军用直升机飞行品质规范》等级1要求(无论是迅猛机动还是有限机动)。采用显模型跟踪法设计的控制律易于实现,具有很高的工程使用价值。