资源一号02D高光谱数据红树林地上生物量反演

黄友菊, 田义超, 张 强, 陶 进, 张亚丽, 杨永伟, 林俊良

1. 广西壮族自治区自然资源遥感院, 广西 南宁 530023 2. 北部湾大学资源与环境学院, 北部湾海洋发展研究中心, 广西 钦州 535000 3. 北部湾大学, 广西北部湾海洋环境变化与灾害研究重点实验室, 海洋地理信息资源开发利用重点实验室, 广西 钦州 535000

引 言

红树林湿地是热带亚热带地区陆地生态系统向海洋生态系统过渡的重要生态系统类型之一[1-3]。 红树林生态系统具有独特的景观格局及其生态过程, 为众多的生物提供了产卵、 索饵和庇护场所, 在提供栖息地、 生物多样性维持、 防灾减灾、 气候调节以及水质净化等方面都发挥着关键作用, 为海岸带地区提供了众多的生态系统服务功能[4-6]。 此外, 红树林具有高生产力、 高归还率和高分解率的性质使红树林生态系统的能量和物质循环高速运行, 这使得红树林成为热带与亚热带地区碳储量最高的植被类型之一, 是地球碳循环的重要组成部分, 其以地球上0.1%的面积固定了大气中5%的碳[7]。 而生物量及生产力的大小是评价红树林碳循环贡献的基础, 准确估算红树林生物量可以评估和追踪红树林碳储量的存量及其变化速率, 对预测红树林在全球碳循环中所起的作用具有重要的意义。 习近平主席在第七十五届联合国大会一般性辩论上提出碳达峰、 碳中和的具体目标, 红树林的固碳能力也被挖掘出来, 因此, 采用定量化评估红树林湿地的生物量, 充分挖掘、 维持与提升红树林的碳汇潜力对实现中国碳中和愿景目标具有重要的理论和现实意义。

实地调查是获取红树林地上生物量(aboveground biomass, AGB)的最基本方法, 虽然此方法可以准确的反映红树林样地尺度上的生物量, 并获取精确的和有价值的红树林地上生物量数据[8-9], 但这种方法在大尺度的红树林地上生物量调查中受到阻碍。 主要是由于红树林生长在淤泥质浅滩以及海陆过渡的潮间地带, 这使得获取红树林实地调查数据成本过高且费时费力; 除此之外, 采用此方法开展大范围的红树林地上生物量调查会对红树林群落的生长环境造成破坏[10]。 近几十年来, 估算区域或更大尺度上的红树林地上生物量主要有两种方法[11-13], 其一是基于模型的方法, 其二是基于遥感的方法。 基于模型的方法主要是通过环境驱动因素和红树林生物量之间的定量关系来反演大尺度上的红树林地上生物量, 然而, 基于模型的方法通常模拟的是潜在的生物量分布, 模拟出的生物量通常与实际分布不一致。 而遥感方法提供了一种间接方法, 通过将地表野外样地观测数据与遥感数据联系起来建立回归模型来获取红树林的地上生物量。 遥感技术的发展极大的提高了大规模和大尺度上的红树林地上生物量监测的效率并降低了野外观测的成本[14-15], 由于这些遥感数据能够捕获生物量的空间变化, 并允许在偏远地区进行重复监测, 因此在估算红树林地上生物量时这些方法变得越来越流行[16]。 目前国内外学者利用遥感技术对红树林地上生物量监测所涉及的卫星数据源主要有中低分辨率的TM/ETM+[17-18]以及高分辨率的IKONOS-2、 WorldView-2以及Quick Bird等[19-20], 这些多光谱遥感数据对红树林地上生物量的估算起到了极大的推动作用, 但是多光谱卫星遥感数据在红树林地上生物量估算中的主要局限性在于其范化的光谱分辨率, 这使得红树林植被冠层的详细反射特性被掩盖。 而高光谱遥感可以通过从可见光到近红外(near-infrared, NIR)或短波红外(short wave infrared radiometer, SWIR)范围内的大量光谱波段获取植被表面的丰富光谱信息, 可在植被冠层尺度上提供有关植被生理以及生化等更详细的信息, 在植被覆盖分类和植被地上生物量估算方面具有一定的潜力。 例如, Sibanda等的研究表明, 高光谱数据在估算生物量方面的精确度比Sentinel-2A多光谱遥感数据要高的多[21]。 但是, 高光谱数据在红树林地上生物量的反演精度如何, 国产高光谱卫星数据在红树林地上生物量的估算中能否应用, 这些问题需要进一步验证。 因此, 结合样地观测数据运用国产高光谱遥感技术对茅尾海地区红树林地上生物量反演是极其必要的。

目前应用于红树林地上生物量的模型主要有参数回归模型[22]和非参数机器学习方法两大类[23]。 参数回归模型方法是以生物量和预测因子之间的假设关系为基础的, 该模型的假设前提是预测变量和生物量之间存在简单的线性关系, 然而这种假设在估算森林地上生物量中往往无法得出令人满意的结果[24]。 非参数机器学习方法如随机森林(random forest, RF)、 支持向量机(support vector machine, SVM)以及KNN神经网络(knowledge neural network, KNN)等算法能够处理非线性关系, 这些方法能够从复杂预测因子之中找出影响森林生物量的关键驱动因素, 从而实现生物量的定量化估算[25], 这类方法目前已经被成功的应用于红树林地上生物量的相关研究中[26]。 如Pham和Brabyn以高分辨率SPOT卫星遥感影像数据为基础, 采用随机森林以及支持向量机等机器学习算法对越南地区的红树林地上生物量进行了估算。 然而像随机森林、 支持向量机以及KNN神经网络这些传统的机器学算法在模型拟合时可能会出现拟合问题, 导致回归模型的稳健性方面存在一定的缺陷[27]。 近年来, 极端梯度提升(eXtreme gradient boosting, XGBoost)算法作为新型的机器学习算法被Chen和Guestrin[28]提出, 该算法能够适应复杂的非线性关系, 模型具有更佳的并行处理能力, 可以有效的解决机器学习模型中可能出现的模型过拟合问题。 但目前不同机器学习算法在亚热带的茅尾海红树林地上生物量中的估算精度如何, 这些机器学习算法能否和国产高光谱卫星结合, 结合之后反演红树林的地上生物量效果如何, 这些问题都需要深入的分析和研究。

茅尾海地区的红树林是我国面积最大、 最为典型的红树林生态系统群落, 该地区的红树林群落主要有外来的无瓣海桑、 当地的秋茄以及桐花树群落, 不同群落的红树林地上生物量空间分布格局如何, 目前都尚未知晓。 目前关于该地区的红树林生物量估算方面的研究还是极其罕见和匮乏的, 很少有学者将样地实测数据和国产高光谱数据相结合, 采用不同的机器学习方法估算不同红树林树种的地上生物量。 鉴于此, 以茅尾海红树林群落为研究对象, 基于实测的红树林野外样方调查数据和国产资源一号02D高光谱数据, 在不同的机器学习算法的支持下对茅尾海的红树林地上生物量进行估算, 在此基础上对比了不同的机器学习算法的性能, 期望研究成果可为茅尾海红树林的生态修复和保护提供科学依据和技术支撑。

1 实验部分

1.1 研究区概况

研究区位于广西钦州北部湾的茅尾海地区(108°28′-108°37′E, 21°48′-21°55′N), 东西长约为18.08 km, 南北长约为14.37 km, 总面积为2 784 hm2。 该区域红树林面积为1 892.70 hm2, 是我国面积最大和最典型的红树林分布区。 该地区主要是以茅岭江、 大榄江和钦江3条入海河流为主, 在多条河流与海水的共同作用下使得在入海口形成泥沙质平滩和潮沟岛屿景观。 该地区气候类型属于南亚热带季风气候, 太阳辐射强, 季风环流明显。 一年分热季(3月-5月)、 雨季(6月-10月)和凉季(11月至次年2月), 全年高温, 各地降水量相差很大, 年均温为21.7 ℃, 年均降水量为1 658 mm, 年平均总日照时数为1 673 h[29]。 该地区的红树林群落主要包括茅岭江沿岸的无瓣海桑和桐花树群落、 大榄江沿岸的秋茄和桐花树群落以及钦江沿岸的桐花树群落(图1)。

1.2 数据来源与研究方法

1.2.1 数据来源

1.2.1.1 野外样地调查

对研究区的红树林进行野外实地踏查, 主要涉及红树林的树种、 栽种模式以及当地潮位信息。 再通过样方调查方法对红树林进行野外数据调查。 通过样方调查方法对茅尾海地区的红树林进行样地调查。 此次共调查了227个样地, 分别为无瓣海桑群落, 桐花树群落和秋茄群落。 根据不同的种群划分不同的样方大小, 如无瓣海桑和秋茄的样方大小设置为10 m×10 m, 桐花树设置为5 m×5 m。 在每个样方内使用卷尺测量每棵树的胸径(在高度1.3 m处测量无瓣海桑胸径, 在0.5 m处测量秋茄和桐花树胸径, 如果桐花树冠幅较小, 测量两个方向的CD, 然后取平均值), 然后使用手持激光测距仪测量树高并利用GPS获取每棵树的经纬度坐标以及样方中心的经纬度坐标。

1.2.1.2 高光谱卫星遥感数据

高光谱资源一号02D卫星数据来源于广西壮族自治区自然资源遥感院。 资源一号02D卫星(5 m光学卫星)于2019年9月12日成功发射, 卫星搭载的两台相机, 可有效获取115 km幅宽的9谱段多光谱数据以及60 km幅宽的166谱段高光谱数据, 其中全色谱段分辨率可达2.5 m、 多光谱为10 m、 高光谱30 m, 高光谱载荷可见近红外和短波红外光谱分辨率分别达到10和20 nm。 图2为茅尾海地区的红树林高光谱数据合成产品, 其中立方体矩形表面的彩色图像是由高光谱图像中的Band74、 Band50和Band5合成, 而剖面则由166个波段构成。

图2 茅尾海红树林高光谱图像颜色立体Fig.2 Color Stereo of hyperspectral image of mangrove in Maowei Sea

1.2.2 研究方法

1.2.2.1 异速生长方程

红树林树种主要有无瓣海桑、 桐花树和秋茄三种树种, 不同的红树林树种伐取难度较大, 并且树龄较长, 伐木的破坏性较大。 鉴于此, 本研究采用异速生长方程计算了茅尾海不同红树林树种的地上生物量, 在计算红树林地上生物量时通过收集前人关于不同红树林树种的具体参数(包括树高、 胸径以及冠层直径等), 随后构建不同树种的异速生长方程。 见表1, 如胡懿凯[30]以无瓣海桑为研究对象, 构建适用于广东省范围内的无瓣海桑生物量模型, 结果模型拟合效果较好, Tam[31]以树高高度和胸径为自变量组合, 回归方程最能估计秋茄和桐花树的生物量。

表1 不同红树林树种异速生长方程Table 1 Allometric growth equation of different mangrove species

1.2.2.2 光谱数据处理

采用Savitzky Golay对每个红树林样地所对应的资源一号02D高光谱卫星数据进行平滑处理。 随后对平滑之后的原始红树林光谱数据进行一阶微分、 二阶微分、 倒数变换、 倒数一阶微分、 倒数二阶微分、 对数、 对数一阶微分、 对数二阶微分、 对数倒数、 对数倒数一阶微分、 对数倒数二阶微分、 倒数对数、 倒数对数一阶以及倒数对数二阶等数学变换, 以增强高光谱数据的有效波谱信息。

1.2.2.3 机器学习算法

选择了机器学习中的三种算法对红树林的地上生物量进行建模, 由于不同的机器学习算法的建模能力有差异, 选择了Boosting算法中的XGBoost、 随机森林回归算法(random forest regression, RFR)以及K近邻回归算法(K-nearest neighbors regression, KNNR)三种算法对红树林的生物量进行反演。 使用python语言包scikit-learn和NumPy建立XGBoost、 RFR以及KNNR回归模型。

(1)XGBoost机器学习算法

极端梯度提升(XGBoost)是由Chen等于2016年提出的一个梯度增强机器学习的新型算法[28]。 XGBoost模型旨在防止过度拟合, 同时通过简化和正则化使得预测保持最佳计算效率而降低计算成本。 XGBoost算法源于“提升”的概念, 它结合了一组弱学习者的所有预测, 通过特殊训练培养强学习者。

(2)RFR随机森林回归算法

随机森林算法RF是由BREIMAN于2001年提出, 是一个树型分类器的集合[32]。 它通过利用Bootstrap方法, 从原始样本集S中进行k次有放回的简单随机抽样, 形成训练样本集。

(3)K近邻回归算法

K近邻回归(K-nearest neighbors regression, KNNR)算法[33], 是机器学习中一个相对简单和基本的模型。 模型的建立仅基于已知样本数据。 通过计算每个样本点附近K个相邻训练样本值的平均值, 确定样本对应的预测值, 即根据样本的相似性预测回归值。

(4)模型精度评估

为了验证不同模型算法预测的红树林生物量与实地调查生物量之间的精度关系, 选择了两个常用的指标进行模型的验证, 这两个指标分别是R2和RMSE。 其中R2越接近1, RMSE值越接近于0, 表示模型的预测的生物量精度越高[34]。

各个变量的计算公式如式(1)和式(2)

(2)

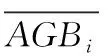
2 结果与讨论

2.1 茅尾海红树林结构参数

茅尾海不同红树林树种样地调查的结构参数如表2所示。 由表2可知, 在三种不同的红树林树种中, 无瓣海桑的红树林树种平均高度最高, 其值可达到9.76 m, 而桐花树的树高次之, 其值多在2 m左右, 秋茄的树高最矮, 其值仅为1.82 m。 就不同的红树林树种冠幅的大小而言, 桐花树的冠幅最大, 无瓣海桑次之, 而秋茄的冠幅最小。 由异速增长方程测算不同红树林树种的地上生物量结果可知, 无瓣海桑的AGB平均值最高(87.66 Mg·ha-1), 变化范围为9.02～305.33 Mg·ha-1, 桐花树AGB次之(52.63 Mg·ha-1), 而秋茄树种的AGB最小。

表2 北部湾茅尾海不同红树林树种结构参数Table 2 Structural parameters of different mangrove species in Maowei Sea of Beibu Gulf

2.2 红树林地上生物量高光谱特征波谱选择

将红树林的原始光谱以及15种光谱变换之后的值与红树林野外样方实测的地上生物量值进行相关分析, 如图3和表3所示, 从图中可以看出红树林原始光谱曲线与地上生物量实测值在40波段之前呈现出负相关关系, 40波段之后则呈现出正相关关系。 而15种变换之后的红树林高光谱曲线与原始的红树林地上生物量的相关系数相比原始的光谱反射率的相关系数有所提升, 说明红树林高光谱数据经过光谱变换之后, 在某种程度上提高了原始光谱的信噪比, 可以在红树林冠层尺度上提供更为有效的关于植被生理和生化等方面的信息。 为了对红树林生物量进行更好的反演以提高模型预测的精度, 我们将显著性水平为0.01的显著相关波段筛选出来作为红树林地上生物量反演的特征波段。

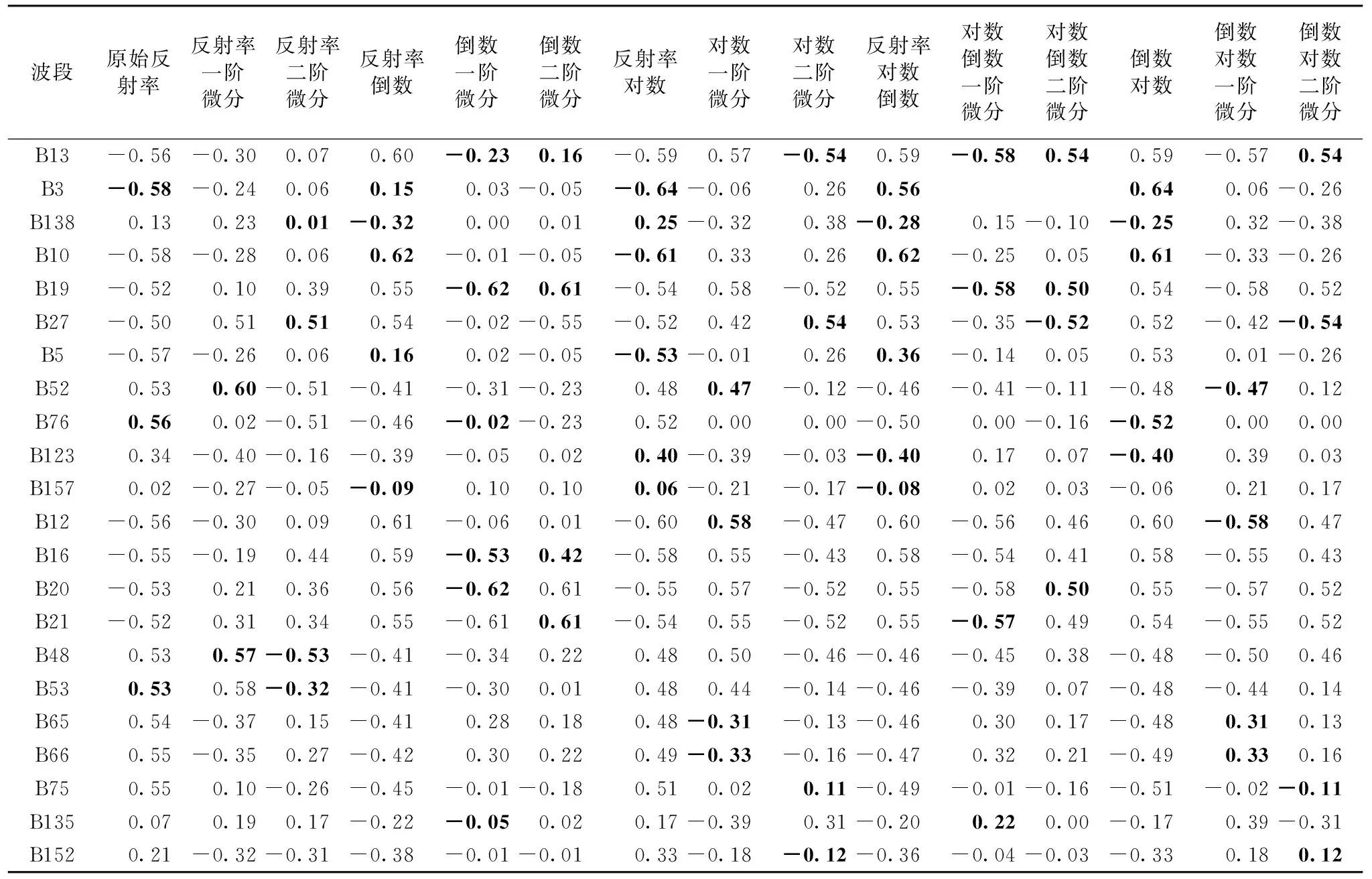
表3 红树林生物量与不同光谱转换初步特征波段相关系数Table 3 Correlation coefficient between mangrove biomass and preliminary characteristic bands of different spectral forms transforms

通过相关系数虽然可以选择出与红树林地上生物量相关性比较高的波段, 但是对红树林地上生物量预测起决定性作用的某些波段信息的筛选还需要更进一步的借助拟合回归方程来确定, 因为有些高光谱波段变量之间有可能呈现出共线性, 对模型来说这些共线性变量可能是冗余变量。 在本研究中我们将相关系数选择出的红树林光谱波段全部放入到逐步回归方程中, 筛选并剔除模型在回归过程中所引起多重共线性的变量, 通过筛选之后, 可以得到预测红树林地上生物量的显著变量(表3)。

表3中的黑体数字是经过逐步回归方程确定的模型最佳预测变量, 我们根据15种不同的光谱变换所获得的光谱波段进行综合比较, 将出现最多次数的波段变量保留, 对重复的共线性变量波段进行整合, 最终筛选并确定了进行红树林地上生物量预测时的11个最佳波段(表4), 分别为B13(499.07 nm)、 B3(413.04 nm)、 B138(2 031.30 nm)、 B10(473.21 nm)、 B19(550.58 nm)、 B27(619.43 nm)、 B5(430.23 nm)、 B52(833.87 nm)、 B76(1 040.20 nm)、 B123(1 778.85 nm)以及B157(2 350.40 nm)。

2.3 红树林地上生物量不同模型预测效果对比

将最终确定的11个最佳波段作为模型输入特征波段, 利用XGBoost、 RFR以及KNNR三种机器学习算法进行红树林地上生物量估算, 并通过R2和RMSE对比模型的运行精度(图4和表5)。

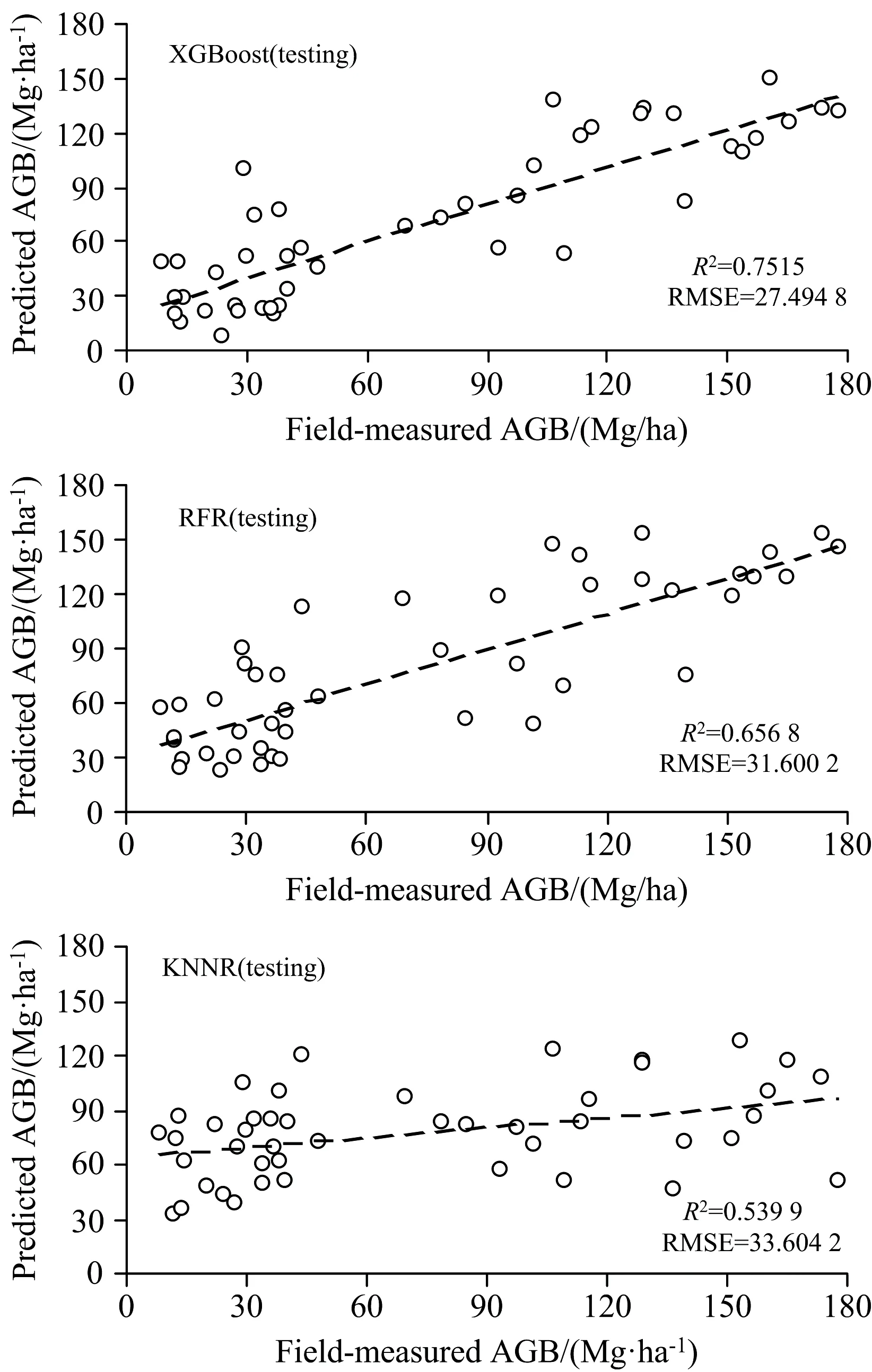
图4 模型训练阶段不同的机器学习模型拟合效果Fig.4 Different machine learning model fitting effects in the model training stage

由不同光谱XGBoost算法的模型训练结果可知, 通过倒数2阶变换的建模精度最高, 其R2=0.964 5, RMSE=9.807 7 Mg·ha-2, 而在模型训练阶段中对数2阶变换的建模精度最低, 其R2=0.948 8, RMSE=12.616 3 Mg·ha-2。 在模型验证方面, 对数倒数1阶变换的模型验证精度最高(R2=0.751 5, RMSE=27.494 8 Mg·ha-2), 而最低的是原始光谱的二阶变换(R2=0.124 3, RMSE=40.402 2 Mg·ha-2)。 虽然倒数2阶变换有最大的R2和最小的RMSE, 但是倒数2阶变换在验证阶段的R2和RMSE结果并不理想, 模型的稳健性和性能较差。 而对数倒数1阶变换在模型的训练阶段和验证阶段均取得了较好的拟合效果, 因此, 经过XGBoost机器学习算法的建模阶段和验证阶段的综合比较之后我们发现, 对数倒数1阶变换为最优模型。

从不同光谱变换形式的RFR算法的结果中可以看出, 在模型训练阶段, 原始的光谱反射率与红树林地上生物量的精度最高, 其R2=0.774 6, RMSE=23.106 6 Mg·ha-2, 而在训练阶段中对数2阶模型的拟合精度较差, 其R2=0.698 7, RMSE=30.610 9 Mg·ha-2。 在模型验证方面, 对数倒数1阶变换的模型验证精度最高(R2=0.656 8, RMSE=31.600 2 Mg·ha-2), 而最低的是对数倒数2阶(R2=0.315 0, RMSE=43.924 5 Mg·ha-2)。 虽然原始的光谱反射率有最大的R2和最小的RMSE, 但是原始光谱反射率在验证阶段可能存在着过度拟合现象, 而对数倒数1阶变换在RF算法模型的训练阶段和验证阶段均取得了较好的拟合效果。

从不同光谱变换形式的KNNR算法的结果中可以看出, 在模型训练阶段, 原始的光谱反射率与红树林地上生物量的精度最高, 其R2=0.653 9, RMSE=28.628 7 Mg·ha-2, 而在训练阶段的对数倒数1阶的拟合精度较差, 其R2=0.295 4, RMSE=41.394 8 Mg·ha-2。 在模型验证方面, 对数倒数变换的模型验证精度最高(R2=0.539 9, RMSE=33.604 2 Mg·ha-2), 而最低的是倒数1阶(R2=0.101 3, RMSE=47.890 2 Mg·ha-2)。 对于KNNR而言, 综合比较模型训练和验证阶段的数据结果之后发现对数倒数变换为最佳的拟合变换。

为了更清晰的表征不同的光谱变换在不同模型中的性能, 绘制了3种机器学习算法在测试阶段的散点图, 如果散点图中的预测值与野外观测的红树林地上生物量实际值越接近1∶1线, 代表模型的拟合精度越高。 由图4可以看出, 基于对数倒数1阶变换的XGBoost模型精度最高, 为最佳的机器学习模型, 其模型在测试阶段R2=0.751 5, RMSE=27.494 8 Mg·ha-2。 基于对数倒数1阶变换的RFR模型精度次之, 其模型在测试阶段R2=0.656 8, RMSE=31.600 2 Mg·ha-2。 而基于对数倒数变换的KNNR模型的拟合效果最差, 其模型在测试阶段R2=0.539 9, RMSE=33.604 2 Mg·ha-2。 因此, 基于对数倒数1阶变换的XGBoost模型是茅尾海红树林地上生物量预测时的最佳模型, 采用对数倒数1阶变换和XGBoost模型能够更好的揭示高光谱变量与红树林地上生物量之间的定量化关系。

2.4 红树林生物量空间分布

基于2.2节选出的11个最佳波段进行对数倒数1阶变换, 将变换之后的波段变量输入到XGBoost模型进行茅尾海红树林地上生物量反演。 由图5可知, 茅尾海红树林地上生物量的预测值范围为4.58～208.35 Mg·ha-1, 平均值为88.98 Mg·ha-1。 从图中可以看出, 茅尾海的西部地区主要以无瓣海桑为优势树种, 该地区的红树林树干高大, 红树林的地上生物量值较高, 而团和岛对岸的无瓣海桑红树林地上生物量则是由其他地方扩展而来, 因此该地区的无瓣海桑红树林地上生物量值偏低。 在研究区中部的大榄江地区主要红树植物是秋茄、 无瓣海桑以及桐花树群落的混生区, 该区域红树林地上生物量值偏低, 其值多在110 Mg·ha-1左右, 而研究区东部的钦江流域入海口地区的红树植物则主要是由桐花树群落组成, 该地区红树林地上生物量偏高, 其值多在180 Mg·ha-1左右。

图5 茅尾海红树林地上生物量空间分布Fig.5 Spatial distribution of aboveground biomass of mangroves in Maowei Sea

3 讨 论

基于资源一号02D高光谱数据, 在优选的11个最佳波段的基础上, 采用3种不同的机器学习算法对茅尾海地区的红树林地上生物量进行反演, 并获得了茅尾海不同地区的红树林地上生物量空间分布格局。 3种机器学习算法的模型性能相差不一, 模型所模拟出的结果有着显著的区域差异性, 致使模拟结果在茅尾海的东部、 中部以及西部地区存在着异质性特征。 有研究表明机器学习算法在红树林生物量估算方面已经被证实相比传统的线性统计回归方法具有一定的优势, 这些算法可以克服多重共线性问题, 并且不要求数据样本满足一定的要求, 且不要求数据服从一定的分布特征[25], 但是不同机器学习算法中模型的特征变量选择及其模型中超参数的选择对模型的预测能力有着非常重要的作用。 Alsumaiti采用随机森林RF算法对阿布扎比泻湖国家公园的红树林地上生物量进行了反演[35], 获得该地区的红树林地上生物量空间分布格局, 但是随机森林对样本的异常值不敏感, 具有最优超参数值的随机森林分类器可能过度拟合训练数据而使得预测的结果产生偏差, 而XGBoost模型中的Boosting算法对异常值非常敏感, 它能灵活的处理各种类型的数据, 在相对较少的调参时间下, 预测的准确度较高[36]。 因此, 在对茅尾海红树林地上生物量进行反演时发现, XGBoost模型的反演能力最强, 在测试阶段R2为0.751 5, RMSE为27.494 8 Mg·ha-1, 其次是RFR随机森林模型,R2和RMSE分别为0.539 9和33.604 2 Mg·ha-1, 而KNNR模型的拟合效果较差, 在训练阶段和测试阶段效果较差。 因此, 在北部湾茅尾海地区, 基于国产高光谱数据采用XGBoost机器学习方法明显优于其他两种算法, 未来可将国产高光谱遥感卫星数据反演红树林地上生物量的相关研究推广到北部湾的其他红树林相关研究中。

由研究结果可知, XGBoost模型反演的茅尾海红树林地上生物量的平均值为88.98 Mg·ha-2, 该值稍微高于野外样方调查的实测平均值, 但是与实地调查值非常接近, 这反映了XGBoost模型的在无瓣海桑红树林地上生物量模拟方面表现出了一定的优势。 无瓣海桑野外样地调查的地上生物量真实值范围为3.86～208.8 Mg·ha-2, XGBoost模型估测的预测值范围为4.58～208.35 Mg·ha-2, 由真实值与预测值的关系可知, 在低生物量范围时, XGBoost模型高估了红树林AGB; 在高生物量范围时, XGBoost则低估了红树林AGB。 尽管本研究采用了新型的机器学习算法对研究区的红树林地上生物量进行反演, 但机器学习算法中不同特征变量所表现出的性能也有所差异, 因此, 也不能完全消除不同特征变量和波段值饱和所带来的影响[37]。 本研究基于XGBoost模型得到的茅尾海红树林地上生物量均值(88.98 Mg·ha-1)比王德智[38]等采用的激光LiDAR方法估算的海南岛红树林地上生物量(119.26 Mg·ha-1)较低, 这可能是海南岛红树林纬度较茅尾海地区红树林纬度低, 水热充足, 物种丰富, 红树林生物量相差较大。 在本研究中, 无瓣海桑地上生物量预测值范围为0～305.33 Mg·ha-1, 平均值为64.82 Mg·ha-1, 该值比深圳福田地区21年生无瓣海桑的估算结果(161 Mg·ha-1)较低[39], 这可能是由于广州地区环境较好, 受人为干扰较少, 无瓣海桑生长较快, 其群落生物量较大。 秋茄是本研究区的劣势树种, 该树种主要分布在茅尾海的大榄江附近, 其生物量预测值为0～108.07 Mg·ha-1, 平均值为29.90 Mg·ha-1, 比福建福鼎地区秋茄群落生物量略小, 其平均值为32.92 Mg·ha-1[40], 这可能也是受纬度水热条件以及红树林滩涂土壤不同的理化性质的影响。 桐花树生物量预测值为0～240.07 Mg·ha-1, 平均值为79.50 Mg·ha-1, 该值高于Cao等[18]在广西沿海地区的红树林生物量(54.40 Mg·ha-1), 这说明当地的桐花树群落生长状况较好, 因此东部地区红树林地上生物量值偏高。

4 结 论

基于国产资源一号02D高光谱数据, 采用极端梯度提升(eXtreme gradient boosting, XGBoost)、 随机森林回归(random forest regression, RFR)以及K近邻回归(k-nearest neighbor regression, KNNR)三种不同的机器学习算法对茅尾海的红树林地上生物量进行了估算。 结果显示:

(1)无瓣海桑的红树林树种平均高度最高, 其值可达到9.76 m, 而桐花树的树高次之, 秋茄的树高最矮, 其值仅为1.82 m。 无瓣海桑红树林地上生物量的平均值最高(90.93 Mg·ha-1), 桐花树次之(52.63 Mg·ha-1), 而秋茄最小(20.27 Mg·ha-1)。

(2)优选并确定了11个红树林地上生物量预测最佳波段, 分别为B13(499.07 nm)、 B3(413.04 nm)、 B138(2 031.30 nm)、 B10(473.21 nm)、 B19(550.58 nm)、 B27(619.43 nm)、 B5(430.23 nm)、 B52(833.87 nm)、 B76(1 040.20 nm)、 B123(1 778.85 nm)以及B157(2 350.40 nm)。

(3)基于对数倒数1阶变换的XGBoost模型精度最高, 为最佳的机器学习模型, 其模型在测试阶段R2=0.751 5, RMSE=27.494 8 Mg·ha-2。

(4)采用XGBoost算法反演茅尾海的红树林地上生物量介于4.58～208.35 Mg·ha-2之间, 平均值为88.98 Mg·ha-2, 红树林地上生物量预测值在空间上呈现出中部低, 两边高的空间分布格局。

致谢:广西壮族自治区自然资源遥感院提供了资源一号02D高光谱遥感影像数据, 北部湾大学资源与环境学院田义超博士提供了北部湾茅尾海红树林样地实测数据, 在此向广西壮族自治区自然资源遥感院以及北部湾大学对本实验的支持表示衷心的感谢。