改进随机蛙跳算法在大豆品种快速鉴别中的应用
李 伟, 谭 峰, 张 伟, 高陆思, 李金山
1. 黑龙江八一农垦大学工程学院, 黑龙江 大庆 163319 2. 黑龙江八一农垦大学信息与电气工程学院, 黑龙江 大庆 163319 3. 黑龙江省农业科学院绥化分院, 黑龙江 绥化 152052 4. 大庆市绿色农产品监测中心, 黑龙江 大庆 163311
引 言
大豆是中国重要的油料和粮食作物, 在国家的农业生产、 粮食安全以及社会发展等领域拥有重要的战略地位[1]。 黑龙江省作为中国大豆的主产区, 具有得天独厚的地理环境和生态气候, 区位优势突出, 肩负着推进大豆产业振兴的重任。 随着大豆杂交技术的广泛应用, 种子品类繁多, 在大豆的种植、 加工、 储存以及流通的过程中极易发生混杂, 直接导致种子质量下降, 体现不出特性优势, 给农民和国家利益造成很大损失。 因此, 快速准确地鉴别大豆品种对于鉴定种子品质, 净化种业市场以及保障粮食安全具有重要意义。
目前, 农作物品种鉴别的传统方法有形态分析法[2]、 化学鉴定法[3]和分子标记法[4]等。 在这些方法中, 形态分析法最为简便, 但需要鉴定者对农作物不同品种的外部形态和内部结构有丰富的认知, 往往受主观因素影响使得鉴别准确度不高。 化学鉴定法、 分子标记法鉴别准确度能够满足需求, 但是存在检测周期长、 过程繁琐以及技术成本高等缺点, 不适宜对样本进行快速批量分析。 而拉曼光谱是一种基于物质分子的散射光谱, 具有“指纹”识别特性, 可以通过谱峰位移、 强度和谱线走势分析物质的组分及其结构变化信息[5]。 与传统鉴别方法相比, 拉曼光谱具有分析速度快、 准确性高、 无需试样制备以及绿色环保等优点, 在农作物品种的快速鉴别中已经得到广泛应用。 Dibs等[6]采集了玉米转基因和非转基因的拉曼光谱数据, 采用线性判别分析(LDA)方法建立品种鉴别模型。 实验结果表明, Whittaker滤波器、 标准正态变换(SNV)和卷积平滑组合(savitzky-golay, SG)卷积平滑组合预处理方法效果最好, 再结合遗传算法(GA)进行特征变量, 所建模型预测准确率最高已达到87.5%。 沙敏等[7]采集糯米、 籼米以及粳米的拉曼光谱数据共计72份, 采用小波变换以及归一化对光谱数据进行预处理, 再结合主成分分析(PCA)、 层次聚类分析(HCA)以及采用支持向量机(SVM)三种不同模式识别方法进行建模分析。 实验结果表明, 采用SVM方法大米品种平均识别率高达98.86%。 Liu等[8]采集了8个糯小麦品种的拉曼光谱数据, 通过MSC、 SG平滑和二阶导数组合方法预处理光谱数据, 再采用主成分分析法(PCA)进行分类判别, 其中校正集预测准确率为94.4%, 验证集预测准确率为94.6%。 然而使用拉曼光谱技术鉴别大豆品种的研究并不多见。
本研究利用拉曼光谱仪采集了黑龙江省4个高蛋白大豆品种(黑农88、 黑农98、 绥农71以及绥农76)的样本数据。 为了去除光谱中冗余和无效波长点对模型预测精度的影响, 提出一种改进随机蛙跳(modified random frog, MRF)算法, 实现大豆品种分类特征信息的有效提取, 再通过偏最小二乘判别分析法(parital least squares discriminant analysis, PLS-DA)构建大豆品种鉴别模型, 以期达到提高品种分类精度的目的。
1 实验部分
1.1 仪器和软件
拉曼光谱数据由奥谱天成(厦门)光电有限公司制造的便携式拉曼光谱仪进行采集, 仪器激发波长为785 nm, 测量范围在200~3 400 cm-1区间, 分辨率为6.58 cm-1。 光谱强度稳定性低于5%, 符合稳定性标准要求。 数据处理软件采用MathWorks 公司的Matlab R2017b 实现。
1.2 样品获取和光谱采集
实验选用黑龙江省2020年主要种植的4种高蛋白大豆种子为研究对象, 品种分别是黑农88、 黑农98、 绥农71以及绥农76, 由黑龙江省农业科学院提供。 从每个品种中随机选取40 粒成熟、 无损伤的种子作为该品种样本集, 4个品种共计160个样本用于光谱数据采集。 拉曼光谱仪采集数据时, 激光功率设为500 mW, 积分时间设为5 000 ms。 对于每个样本连续进行3次采集, 将平均光谱作为该样本的原始光谱数据。
1.3 方法
1.3.1 随机蛙跳算法
随机蛙跳(random frog, RF)算法[9]借鉴可逆跳跃马尔可夫链蒙特卡罗(reversible jump Markov Chain Monte Carlo, RJMCMC)算法的思想, 建立了一种数学上简单并且计算效率高的特征波长选择算法。 RF通过在模型空间中实现固定维度和跨维度移动搜索获得一个伪MCMC链, 用于计算每个特征变量的被选概率, 作为该特征变量选择的标准, 主要包括以下三个步骤[9]:
(1) 参数初始化:K0为初始变量集F0的个数, 在1~P之间随机设置(P为全部变量个数); 迭代次数N为10 000;θ为正态分布控制参数, 取默认值0.3;ω为大于1的候选变量个数控制参数, 取默认值3;η为接受概率, 取默认值0.1。
(2) 候选变量子集构造: 通过N(K0, 0.3K0)产生一个随机数, 就近取整确定为候选子集变量个数K*, 进而构造一个包含K*个变量的候选子集F*,F为包含全部p个变量的集合。
① 若K*=K0, 则F*=F0。
② 若K* ③ 若K*>K0, 则先从F-F0中随机选取3(K*-K0)个变量, 并与F0构成新变量子集T后建立PLS-DA模型, 保留模型中回归系数绝对值最大的K*个变量构成候选子集F*。 候选变量子集F*初选后, 判断其是否被接受进行下一次迭代。 分别用F0和F*构建偏最小二乘分析模型, Err0和Err*为两个模型的预测误差。 如果Err*≤Err0, 则接受F*作为F1, 否则以0.1Err0/Err*的概率接受F*作为F1。 用F1代替F0, 进行下一次迭代计算, 直到结束N次循环。 (3) 变量选择概率计算: 经过N次迭代计算共获取N个变量子集。Nj表示第j个变量在N次迭代中被选择的次数。 则每个变量被选择概率根据式(1)进行计算 (1) 由式(1)可知, 变量越重要被随机蛙跳算法选择的概率就越大。 因此, 该被选概率可以作为衡量变量重要性的指标。 通过设定不同阈值, 选取被选概率大于阈值的变量作为特征波长变量, 对比所建模型性能从而确定最优特征波长。 1.3.2 改进随机蛙跳算法 在采用RF算法提取特征变量时, 由于初始变量集F0是从原始数据集中随机抽取产生的, 可能会引入无用或干扰波长变量, 使得算法的预测能力和收敛速度降低。 因此, 为了提高初始变量集的有效性, 提出一种基于最小绝对收敛和选择算子(least absolute shrinkage and selection operator, LASSO)的改进随机蛙跳算法。 LASSO[10]是一种基于普通偏最小二乘法的特征波长选择算法, 通过增加L1范数惩罚, 在预测残差平方和最小准则下, 将模型的回归系数的绝对值之和限定在一个常数范围内, 从而将一些不重要变量的回归系数严格收缩为0。 多元线性回归分析模型如式(2) Y=Xβ+ε (2) 式(2)中,X=[x1,x2, …,xn]T∈Rn×m为大豆样本组分变量,Y=[y1,y2, …,yn]T∈Rn×1为样本对应品种属性, 其中,m为样本的特征变量数,n为大豆样本数量。β=[β1,β2, …,βm]T∈Rm×1是回归系数向量。 LASSO准则的目标函数如式(3) (3) 式(3)中,λ1为L1正则化系数, 当λ1=0时为常规最小二乘法, 当λ1逐渐增大时L1正则化影响也越大, 越来越多的系数将接近于0或者等于0,λ1的取值将根据RMSECV取最小值时确定。 LASSO算法可以筛选与属性变量最相关特征变量, 采用该方法提取大豆重要特征波长点作为RF初始变量集F0, 可以有效消除初始变量的随机性, 在此基础上开始迭代计算, 可以改善RF算法所需迭代次数大、 算法收敛慢等问题。 同时, RF算法通常选取概率排序1~10的变量, 或者选取概率大于某一阈值的变量, 因此提取的特征波长往往具有不确定性。 改进方法如下: 首先去除选择概率为0的变量, 对于排序后变量以10个波长点为间隔, 每次增加1个间隔构建波长变量与大豆品种属性的偏最小二乘分析模型。 然后计算每个模型的RMSECV找到最优特征波长以提高模型的预测性能。 1.3.3 ElaticNet特征选择方法 ElaticNet方法结合了LASSO回归和岭回归的思想, 在普通最小二乘回归基础上增加L1惩罚和L2惩罚, 可以同时对变量系数的绝对值和平方项进行压缩。 LASSO回归对所有波长变量的回归系数进行同等程度的压缩, 则可能由于过度压缩导致模型的预测准确度下降。 岭回归[11]是通过增加L2惩罚, 收缩不重要变量回归系数以达到提高预测准确度的目的, 但不具有变量选择的能力。 Elastic Net结合这两种惩罚函数的特点, 在高维数据的情况下剔除冗余变量, 且一般不会过度压缩回归系数, 从而达到提高模型预测精度的目的。 Elastic Net准则的目标函数如式(4) (4) 令α=λ1/(λ1+λ2),λ=λ1+λ2, 则式(4)为 (5) 从式(5)中可以看出, 当α=0时为岭回归, 当α=1为LASSO回归, 当α∈(0, 1)时为Elastic Net回归, 它是L1和L2惩罚的特殊线性组合, 采用α的大小来调节它们之间的权重。 当λ=0时为普通最小二乘法, 当λ逐渐增大时正则化的影响也将越大,λ的取值将根据RMSECV取最小值时确定。 1.3.4 模型构建方法与评价 PLS是在主成分回归基础上提出的多元校正方法, 在计算主成分时, 考虑主成分方差尽量最大以提取有用信息, 同时还保证主成分与样本属性变量尽可能地相关, 使得所建模型具有较高的预测精度和较强的稳健性。 因此以改进随机蛙跳法选择后的特征波长为输入变量, 使用PLS-DA方法建立大豆品种鉴别模型。 并采用均方根误差(root mean square error, RMSE)、 决定系数(coefficient of determination,R2)和准确率(accuracy)三个指标对模型效果进行评价。 RMSE值越小, 样本预测值与实际值之间的差异越小,R2越接近1, 样本预测值与实际值之间的相关度越高, 表明模型的预测性能越好。 对于识别正确率, 分别将黑农88、 黑农98、 绥农71以及绥农76四个大豆品种样本赋值 1、 2、 3、 4, 根据文献[12], 将PLS-DA鉴别模型的误差阈值设置为±0.5, 结果分别在1±0.5、 2±0.5、 3±0.5和4±0.5之间时, 大豆样本识别正确, 否则识别错误。 大豆样本的原始拉曼光谱如图1(a)所示。 标准正态变换(standard normal variate transformation, SNV)[13]是一种有效的预处理方法, 可以校正样本不均匀带来的散射效应对光谱数据的影响, 预处理效果如图1(b)所示。 再利用KS (Kennard-Stone)算法按照3∶1的比例划分大豆样本集, 则校正集样本为120个、 预测集样本为40个。 采用PCA方法对校正集和预测集的共160个大豆拉曼光谱数据进行降维处理, 第一、 第二和第三主成分的贡献率分别为88.56%、 4.65%和3.45%, 前三个主成分的累积贡献率达到96.66%, 说明可以反映原始样本所提供的绝大多数信息。 采用前三个主成分绘制大豆样本校正集和预测集的得分图如图2所示, 可知校正集和预测集的样本分布比较均匀, 校正集能够覆盖预测集, 说明该样本划分方法有效并可以用于建模分析。 图1 大豆原始及预处理后拉曼光谱图(a): 原始拉曼光谱; (b): SNV预处理后拉曼光谱Fig.1 Raw and SNV pre-processed Raman spectra of soybean(a): Raw Raman spectra; (b): SNV pre-processed Raman spectra 图2 大豆样本前三主成分得分图Fig.2 Score plot of the top three PCA for soybean samples 2.2.1 RF特征波长优选 表1 不同阈值的优选波长Table 1 Optimized wavelengths with different thresholds 图3 RF算法的波长被选概率Fig.3 Selected probability of each wavelength by RF 2.2.2 MRF特征波长优选 采用LASSO算法对大豆全光谱数据进行初选。 正则化参数λ1通过10折交叉验证法确定, 首先将预处理后大豆样本数据划分为10份, 每次选取其中9份作为校正集, 剩余1份作为预测集, 采用LASSO方法选择特征波长建模并计算每个模型均方根误差, 经过10次迭代计算后取其平均值作为最终RSMECV值。 当λ1=0.003 0时, RMSECV最小为0.195 8, 此时共提取了106个与大豆品种属性最相关的特征变量, 将其作为RF算法的初选变量集F0, 开始进行迭代计算。 将MRF算法的迭代次数分别设置为1 000、 1 500、 2 000和2 500次, 运算结果如表2所示。 表2 不同迭代次数的优选波长Table 2 Optimized wavelengths with different iteration times 对于不同迭代次数选取的特征波长, 首先去除被选概率为0的波长点, 对剩余波长进行排序后以10个波长点为间隔, 每次增加1个间隔建立PLS-DA模型, 选择RMSECV取最小值时的波长组合为优选特征波长。 由表2可知, 当迭代次数为2 000次时, 不同波长组合的RMSECV计算结果如图4(a)所示, RMSECV值最小时为0.111 0, 最终选取300个有效特征波长点, 如图4(b)所示。 图4 MRF特征波长优选结果(a): 特征波长组合的RMSECV值; (b): 优选特征波长分布Fig.4 Results of MRF characteristic wavelength optimization(a): RMSECV of characteristic wavelength combinations; (b): Distributionof optimized characteristic wavelength 2.2.3 ElasticNet特征波长优选 由式(5)可知, ElasticNet的优化函数L(β)包含参数α(0<α<1)和正则化系数λ(λ>0)。 通过10折交叉验证法确定调节参数α, 由表3可知, 当参数α取0.016时, RMSECV值最小为0.145 6, 此时最优正则化系数为λ=0.031 7。 基于所选最优参数(α=0.016,λ=0.031 7), ElasticNet法通过坐标下降法(coordinate descent)迭代计算3201个大豆拉曼光谱数据的稀疏系数, 非零稀疏系数对应成分变量即为所选特征波长点, 通过ElasticNet法共选择了1 345个大豆特征波长点, 波长分布如图5所示。 表3 调节参数α选择Table 3 Selection of adjustment parameter α 图5 ElasticNet选择的特征波长分布Fig.5 Characteristic wavelengths distribution by ElasticNet 将预处理后大豆光谱数据, 分别采用RF、 MRF、 LASSO和ElasticNet算法进行特征波长提取, 将这4种方法得到的特征波长点以及全光谱数据作为预测模型输入变量, 大豆品种属性作为输出变量, 建立大豆品种鉴别的PLS-DA模型, 各模型鉴别结果如表4所示。 表4 不同波长选择方法的模型对比Table 4 Model comparisons of different wavelength selection methods 提出的MRF特征波长优选方法具有高效的全局搜索能力, 可以有效改善RF算法初始变量集随机性、 所需迭代次数大、 阈值选取不确定的问题。 利用该方法结合拉曼光谱建立黑龙江省高蛋白大豆品种的PLS鉴别模型, 并与全光谱以及RF、 LASSO和ElasticNet算法提取的特征波长建模结果进行对比分析。 通过MRF波长选择方法, 可以有效地剔除无关波长点, 简化模型结构, 而且模型的预测性能得到一定程度地提升, 识别准确率达到100%, 为黑龙江省大豆在种植、 加工、 储存与流通过程中的品种快速鉴别提供了一种新思路。 在后续研究中, 应进一步增加不同产地、 不同品种的大豆样本数量, 以提高鉴别模型的稳健性和泛化能力, 以期在实际应用中取得良好效果。2 结果与讨论
2.1 样本光谱数据分析


2.2 拉曼光谱特征波长优选







2.3 模型构建结果评价与分析

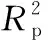
3 结 论

