计及不同控制方式的混合直流多馈入系统电网强度评估

江俊贤，陈启超，王菲，王奕鑫，李辰，王冠中

(1.浙江大学 电气工程学院，浙江 杭州 310027；2.国网经济技术研究院有限公司，北京 102209；3.国网江苏省电力有限公司经济技术研究院，江苏 南京 210008；4.山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061)

我国能源资源与负荷需求在地理分布上具有高度逆向的特征，为了实现跨区域电力传输，发展了大规模高压直流(high voltage direct current,HVDC)输电工程.随着基于电网换相换流器的高压直流输电(line commutated converter based HVDC,LCC-HVDC)规模的增加，直流多馈入系统(multiinfeed HVDC system,MIDC system)受端交流电网的电压支撑强度相对降低（简称电网强度），系统存在电压失稳风险[1-3].基于电压源型换流器的高压直流输电(voltage source converter based HVDC,VSC-HVDC) 相较LCC-HVDC 具有无需电网换相、无功补偿的优势，使得MIDC 系统逐步发展为混合直流多馈入系统(hybrid multi-infeed high voltage direct current system,HMIDC system).HMIDC 是我国未来新型电力系统交直流系统的典型模式，因此准确量化HMIDC 电网强度对受端电网的安全稳定运行至关重要[4-6].

短路比(short circuit ratio,SCR)被广泛用于量化LCC-HVDC 单馈入系统(single infeed HVDC system，SIDC system)的电网强度[7].在MIDC 系统中，现有电网强度评价指标分为以下2 类.第1 类为电路等值类评估指标，主要包括多馈入短路比(multi-infeed short circuit ratio,MISCR)[8-9]与等值有效短路比(equivalent effective short-circuit ratio,EESCR)[10].现有研究表明电路等值类评估指标沿用经验值为交流电网强度临界值将导致分析结果偏保守.第2 类为交流网络模态解耦类指标，比如广义短路比(generalized short-circuit ratio,gSCR)[11].辛焕海等[11]针对直流设备侧参数与控制方式相同的LCC-HVDC 同构MIDC 系统(简称同构系统)，利用严格的特征值分解，得到系统模态与交流网络特征的显式关系，推导得到gSCR 指标，gSCR 临界值由直流侧参数决定且与SCR 临界值在不同网架下能够保持一致.

在混合直流馈入系统的电压稳定性研究中通常将VSC-HVDC 近似为功率源或恒阻抗处理[12-16]，重点关注LCC-HVDC 节点端口特性对电网强度的影响.郭春义等[13]通过电路等值前后混合直流双馈入系统中LCC-HVDC 的传输功率保持不变推导LCC-HVDC 系统短路比的视在增量，以评估混合直流多馈入系统中LCC-HVDC 的系统强度.田宝烨等[15]在混合双馈入系统中的LCC-HVDC直流电流上施加扰动，将VSC-HVDC 电压变化量与电流变化量的比值定义为运行阻抗，通过阻抗等值构造LCC-HVDC 单馈入系统，以评估混合直流双馈入系统中VSC-HVDC 对LCC-HVDC 系统强度的影响.倪晓军等[14,16]基于小信号模型计算VSC-HVDC 的等效阻抗，提出基于阻抗的有效短路比衡量混合直流多馈入受端电网的强度.上述指标的提出在一定程度上完善了混合直流馈入系统中电压稳定性的分析理论，然而现有的混合直流多馈入系统的强度评估指标存在以下不足：混合直流多馈入系统的建模基于双馈入系统，没有泛化到多馈入系统，弱化了指标在工程中的适用性；仍是基于电路等值思想的短路比指标概念的拓展，指标缺乏明确的临界值.

现有研究尚未基于网络模态解耦思想给出混合直流馈入系统电压稳定裕度的评估方法.为此，本研究进一步弱化辛焕海等[11,17]所提网络模态解耦类指标所需的同构直流多馈入系统的假设条件，将其应用于直流设备侧参数与控制方式存在差异的（简称异构）直流多馈入系统与混合直流多馈入系统.基于模态摄动理论，推导计及控制方式与参数异构的MIDC 系统电网强度临界值计算方法.此外，给出考虑VSC-HVDC 设备后HMIDC 系统电网强度近似评估流程.最后，通过仿真算例验证分析方法的有效性.

1 LCC-HVDC 同构多馈入系统电网强度

1.1 LCC-HVDC 系统建模

交直流系统稳定性分析采用LCC-HVDC 单馈入系统，其等效电路如图1 所示.图中，K、Pd、Ud、Id、E、γ、X、N、φ、Qd和Cc分别表示直流侧变压器变比、有功功率、电压、电流、电动势、关断角、变压器短路电抗、串联变流器数目、功率因数、无功功率和补偿电容，U、θ 与Z分别表示换流母线电压幅值、相角以及交流电网戴维南等值阻抗.

在LCC-HVDC 准稳态方程组[18]基础上采用标幺化方法[19]建立系统模型：

式中：k为直流侧电压基准值与交流侧电压基准值的比值，在计算时可以直接代入各变量标幺值进行计算；ω 为角频率.

交直流系统的电压稳定研究侧重于分析LCC-HVDC 的最大传输功率.在量化LCC-HVDC馈入系统的功率传输极限时，可以通过雅可比矩阵鞍结分岔进行表征，即采用三端口雅克比矩阵JS的奇异性作为判据[20-21]：

式中：Δ表示微增量，J表示对应变量的偏导数，单馈入系统中JS表达式详见文献[11].

进一步，在鞍结分岔点处，式(2)中的3 阶雅克比矩阵奇异性等价于降阶雅可比矩阵JLCC+JAC的奇异性[17]，即 d et(JS)=det(JLCC+JAC)，JLCC、JAC分别表示直流侧与交流侧雅可比矩阵.直流多馈入系统中交流侧雅克比矩阵JAC不受LCC-HVDC控制方式的影响，可以统一表示为

式中：d iag 表示对角矩阵，B表示交流侧等值导纳矩阵，下标i对应第i回直流.

直流侧雅克比矩阵JLCC可以表示为

1.2 同构MIDC 系统电压稳定性分析方法

当LCC-HVDC 在CP-CEA 和CC-CEA控制时，LCC-HVDC 的功率传输极限受到电网强度的制约.在实际工程中，LCC-HVDC 在正常运行情况下，一般采用CP-CEA 或CC-CEA 控制，以应对系统中负荷潮流的变化，提高系统运行的灵活性.因此，Zhang 等[17]基于模态解耦理论给出考虑CPCEA 和CC-CEA 控制下的直流多馈入系统电网强度的评估方法.

针对CP-CEA/CC-CEA 控制方式下的同构LCC-HVDC 多馈入系统，式(4)中的各个直流馈入处的Ti与oi均相等（即T=T1=···=Ti，o=o1=···=oi），此时JLCC+JAC矩阵奇异等价于Jsys奇异.表达式如下：

式中：In为单位矩阵，Jeq表示拓展导纳矩阵.

根据矩阵特征值分解，在位于鞍结分岔点时，式(5)对应的临界稳定条件能够简化为

最小特征值 λ1在分岔点的临界值由直流侧端口特性T与运行点o决定，求解式(6)可得λ1的临界值即当λ1=λc时，系统发生鞍结分岔，LCC-HVDC 到达最大传输功率，当o=1 时，系统额定运行点到达电压稳定边界；当 λ1＞λc时，系统尚未达到分岔点，通过计算 λ1与λc的差值能够判断系统的稳定裕度[17].

综上，现有网络模态解耦类指标仅给出了CP-CEA/CC-CEA 控制方式下同构MIDC 系统的电网强度定义方法，尚未考虑定功率定直流电压(constant power constant voltage,CP-CV)和定直流电流定直流电压(constant current constant voltage,CC-CV)控制方式.

2 LCC-HVDC 异构多馈入系统分析

2.1 端口特性参数对电压稳定性的影响

在考虑CP-CV/CC-CV 控制方式时，系统临界稳定条件的形式不变，仍为式(5)中的矩阵形式，但是，决定临界值 λi的直流侧特性参数Ti随控制方式变化.在CP-CV/CC-CV 控制方式下，直流端口特性Ti=(ci-cos γ)PdiK(ci)+2ωCcUi2/Pdi.基于GIGRE 标准模型参数计算LCC-HVDC 不同控制方式下Ti的具体数值：在CP-CEA/CC-CEA 控制方式下，Ti=1.486；在CC-CV/CP-CV 控制方式下，Ti=-1.238.结合灵敏度矩阵[22]符号特征可知，LCCHVDC 直流端口特性Ti对交流电网主导模态存在定性影响，其中正的Ti会恶化系统的电压稳定性，而负的Ti能够提高系统的电压稳定性.综上，即CP-CEA/CC-CEA 控制不利于系统稳定，CP-CV/CC-CV 控制有利于系统稳定.

进一步分析参数对直流端口特性的数值影响，根据邵瑶等[8]的分析结论可知，L C CHVDC 端口特性主要受到变压器短路电抗X与熄弧角 γ的影响，考虑参数变化范围：X=0.15～0.20，γ=15°～21°.仿真结果表明：CP-CEA/CC-CEA 控制方式下Ti数值变化范围为1.238～1.535，CP-CV/CCCV 控制方式下数值变化范围为-1.261～-1.146.正常运行范围内直流侧参数变化难以改变Ti的正负号.

2.2 LCC-HVDC 异构多馈入系统电网强度

2.1 节分析结果表明，交直流系统电压稳定性主要受CP-CEA/CC-CEA 控制方式的制约，因此在电网强度评估中将其作为主要矛盾，同时对其他控制方式做近似分析.主要分析思路如下：将CCCV/CP-CV 控制下的LCC-HVDC 通过网络侧折算反映其对电网强度的提升作用；将CP-CEA/CCCEA 控制方式下的LCC-HVDC 仍保留在直流侧，通过模态摄动法量化其对电网强度临界值的影响.

首先分析CP-CEA/CC-CEA 控制下LCC-HVDC异构多馈入系统的电压稳定性，采用模态摄动法[23]进行分析.

类比式(5)，异构系统的Jsys可以表示为

引理1假设 λa为矩阵M的单特征值，且存在左右特征向量uL、uR，令 Δ为矩阵M的扰动，并通过O(‖Δ‖) 表示矩阵Δ的高阶小量，那么扰动后的矩阵 ΔM存在特征值，满足

引理1 可以作为 CP-CEA/CC-CEA 控制方式下异构系统电网强度评估理论依据.

对式(5)中LCC-HVDC 同构多馈入系统最小特征值进行摄动，得到LCC-HVDC 异构多馈入系统雅克比矩阵Jsys的最小特征值：

det(Jsys)=0的等价表达式如下：

工程经验表明，LCC-HVDC 系统参数差异导致Ti的数值变化程度相较解耦后的交流网络模态λi而言较小，即满足摄动理论的条件，近似误差

求解式(11)能够得到异构系统中 λc解析表达式：

式中：λc为方程(11)的正根，为异构直流多馈入系统中各个LCC-HVDC 换流器oiTi通过特征向量加权后的结果.

由2.1 节的分析结果可知，CC-CV/CP-CV 直流侧端口特性对电压稳定性有支撑作用，其对电压稳定性的影响可以通过网络侧近似表征.根据上述分析，计及全部控制方式的LCC-HVDC 异构多馈入系统的电网强度评估步骤如下.

1）按照直流控制方式，将多馈入直流系统的节点导纳矩阵B划分为动态保留子块（对应CCCEA/CP-CEA 控制方式下的LCC-HVDC）与网络保留子块(对应CC-CV/CP-CV 控制方式下的LCCHVDC)：

式中：BCEA为动态保留子块，BCV为网络保留子块，Bin表示联络导纳块.

2）将BCV向左上角做Schur 补，得到等效后的导纳矩阵：

3)计算矩阵 d iag(PNi)Bred的最小特征值 λ1及其对应的左右特征向量.

4）利用式(12)计算 λc.

5）通过λ1-λc量化系统的稳定裕度.

3 HMIDC 系统电网强度评估方法

将VSC-HVDC 的接入等效成对原有异构LCC-HVDC 直流多馈入系统网络部分的摄动，以此将VSC-HVDC 与LCC-HVDC 异构直流多馈入系统的稳定裕度量化问题转换成异构LCC-HVDC系统的稳定裕度量化问题，从而基于第2 节的理论基础通过特征值数值大小来刻画系统的稳定裕度.

VSC-HVDC 直流侧雅可比矩阵[23-24]统一表示为

式中：Pv、Qv分别表示VSC-HVDC 的有功功率和无功功率.

在定量评估系统稳定裕度时，将VSC-HVDC与LCC-HVDC 的直流侧端口特性叠加，基于如图2所示的计算流程能够得到混合直流馈入系统的雅克比矩阵：

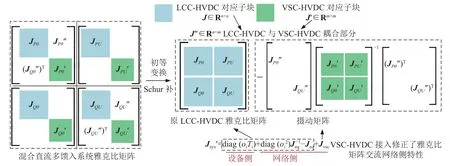
图2 考虑VSC-HVDC 后的系统雅克比矩阵的分析流程Fig.2 Analysis flow of system Jacobian matrix considering VSC-HVDC

式中：Jvsc表示VSC-HVDC 接入后对原异构LCCHVDC 系统雅克比矩阵的摄动量.

根据引理1，对式(5)异构LCC-HVDC 系统的最小特征值进行摄动，可以得到混合直流多馈入系统雅可比矩阵Jsys的最小特征值：

进一步，式(17)可以表示为

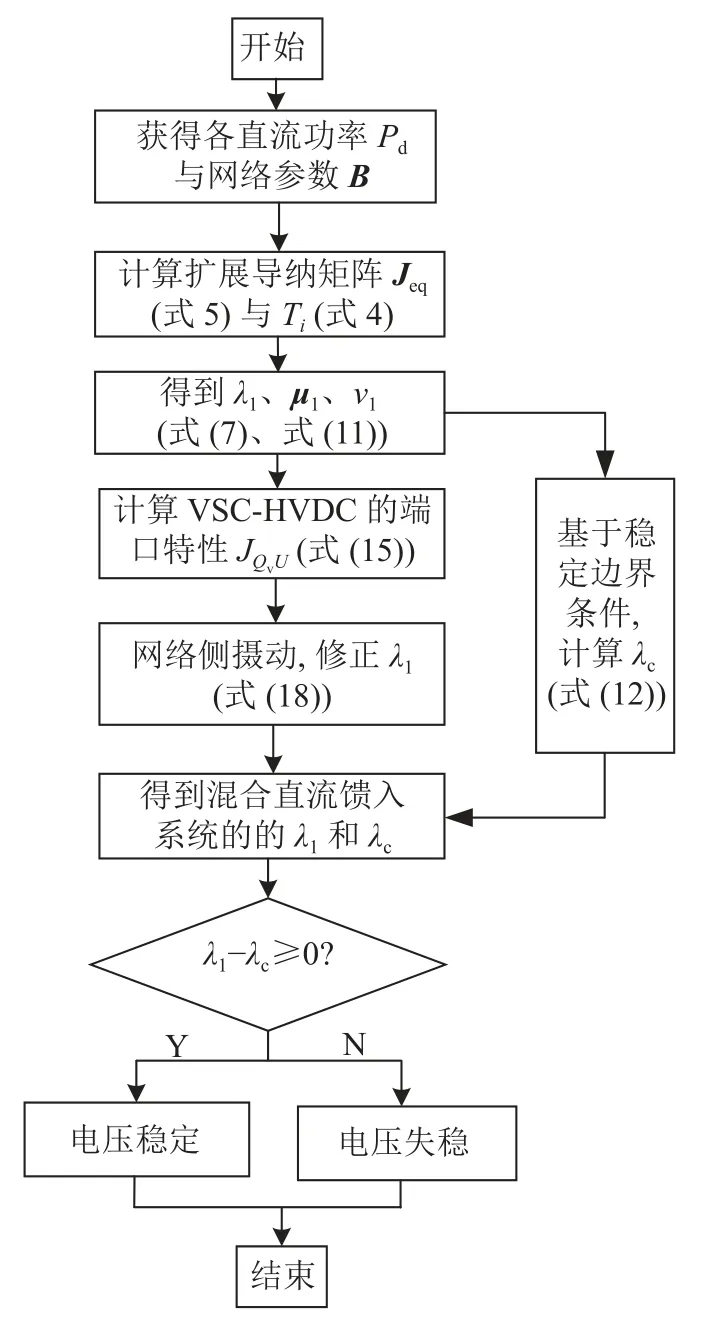
图3 混合直流多馈入系统电压稳定性评估流程Fig.3 Static voltage stability evaluation process of HMIDC

基于特征值灵敏度[25]，从物理空间上分析直流联络导纳与直流功率对系统强度的影响，主导模态 λ1对等值导纳的灵敏度为

类似的，主导模态 λ1对直流容量的灵敏度为

基于上述灵敏度分析结果可知，系统强度的提升能够通过增大直流间联络导纳或减小直流容量来实现.

4 算例分析

基于MATLAB 与PSCAD/EMTDC 仿真平台，分别搭建三馈入异构LCC-HVDC 系统与混合直流馈入系统模型，完成数值计算与动态仿真，验证分析方法的有效性.

4.1 强度评估指标有效性验证

基于第2 节的分析方法评估异构L C CHVDC 系统的电压稳定性.仿真选用的异构三馈入LCC-HVDC 系统的网络侧参数与设备侧参数见表1、2.算例选取直流额定容量为1 000 MV·A，交流与直流电压基准值分别为230、500 kV.

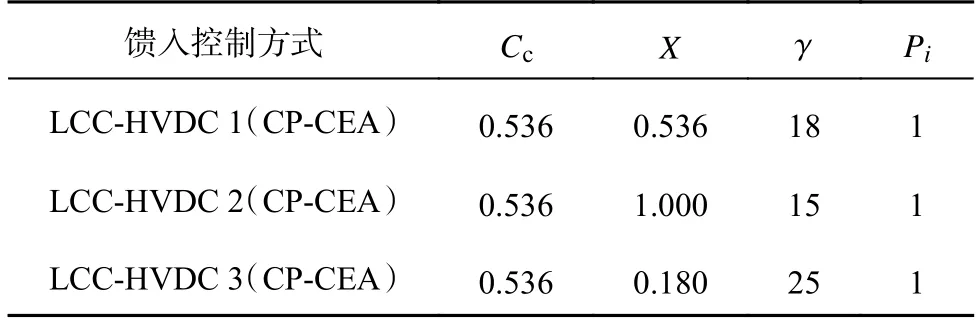
表1 LCC-HVDC 三馈入系统直流侧参数Tab.1 DC side parameters of LCC-HVDC triple-infeed system

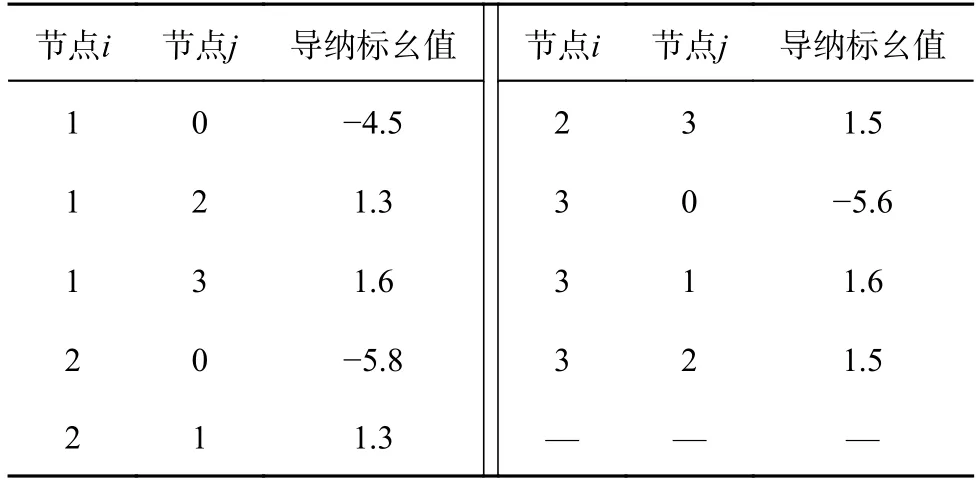
表2 LCC-HVDC 三馈入系统交流侧等值参数Tab.2 AC equivalent parameters of LCC-HVDC triple-infeed system

验证特征值用于评估系统电网强度的适用性，即能否通过 λ1-λc的数值评估异构L C CHVDC 系统的稳定裕度.在异构直流三馈入系统中，保持Pd2与Pd3为1.0p.u.，增加Pd1以改变电网强度，λ1和 λc随Pd1的变化结果如图4所示.可以看出，随着Pd1的增加，λ1减小，λc基本维持恒定，由λ1和 λc之间的差值量化的稳定性裕度随着Pd1的增加而减小.当Pd1增加到功率传输极限时，λ1与λc重合，此时交直流混联系统到达分岔点，系统稳定裕度为0.当Pd1大于功率传输极限时，λ1＜λc，系统失稳.

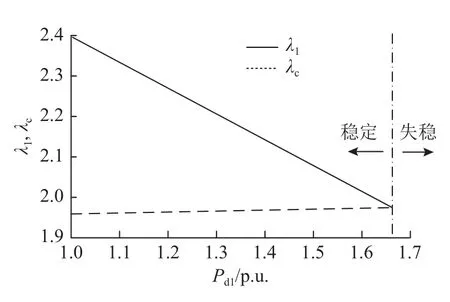
图4 电网强度随直流功率的变化曲线Fig.4 Variation curve of grid strength with DC power

基于第3 节给出的分析方法评估混合直流三馈入系统中的电压稳定性.混合直流三馈入系统参数详见表3、4.表中，各参数均为标幺值，τ 为变压器分接头，PN、QN分别为额定直流功率、额定无功功率.

表3 混合直流三馈入系统直流侧参数Tab.3 DC side parameters of hybrid triple-infeed system

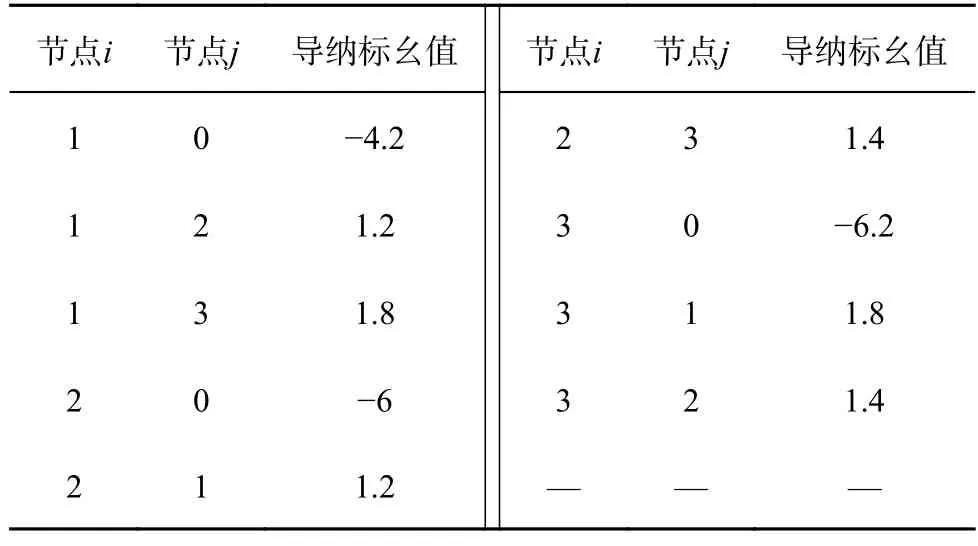
表4 混合直流三馈入系统交流侧等值参数Tab.4 AC equivalent parameters of hybrid triple-infeed system

在仿真模型中将Pd1从额定值增大，计算λ1的数值大小，并通过系统雅克比矩阵奇异det(Jsys)=0表征电网强度临界值，以此计算Pd1的功率传输极限，由仿真结果可知，Pd1=1.572 时到达功率传输极限，此时d et(Jsys)=0，当Pd1＞ 1.572 时，λ1＜ λc，系统发生电压失稳.进一步，通过式(18)计算分岔点处的 λ1=2.17，与通过式(12)计算得到的理论临界值λc=2.11 接近，数值误差为2.84%.

4.2 异构三馈入系统动态仿真

基于4.1 节的异构三馈入LCC-HVDC 系统完成时域仿真，算例选取直流额定容量为1 000 MV·A，交流基准值分别为230 kV，仿真得到的 λc=2.05，与4.1 节的数值计算结果1.98 接近.此外，将LCCHVDC 3 控制方式改为CC-CV 后，异构LCCHVDC 三馈入系统的时域仿真结果如图5、6 所示.图中，数值均为标幺值，Uac表示母线交流电压幅值.对应 λc=1.64，与理论临界值1.57 接近.由仿真结果可知，在控制方式修改为CC-CV 后，λc减小至1.64，λ1-λc数值增大，系统稳定裕度增大.

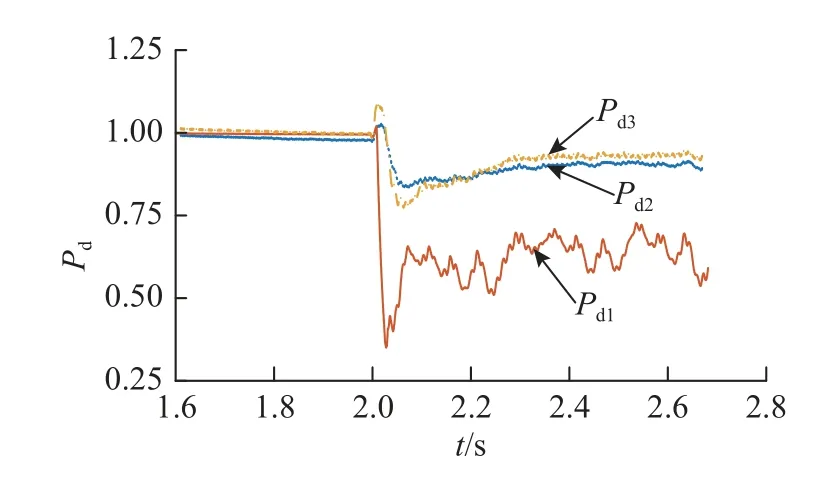
图5 MIDC 系统功率变化曲线Fig.5 Power curves in MIDC system

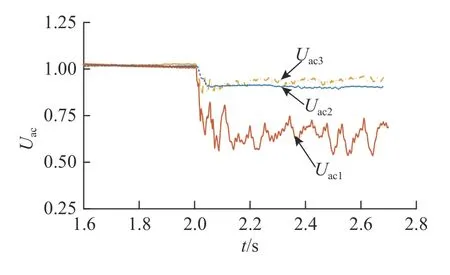
图6 MIDC 系统电压变化曲线Fig.6 Voltage curves in MIDC system

进一步，通过时域仿真验证分析结论.在混合直流三馈入系统中设置初始运行点为P1，直流功率Pd1=1.53，此时 λ1=2.23＞λc，在t=2 s 时将运行点更改为P 2，对应的直流功率指令值增加到1.59p.u.以改变系统强度并观察系统的响应过程.由上文分析结果可知，1.59 ＞Pdmax，此时λ1＜λc，即运行点为P2 时无法维持系统稳定，运行点由P1 改变为P2，系统对应的动态响应过程如图7 所示.图中，Pd1ref为直流功率参考值.仿真结果表明，系统在初始运行点P1 能够维持稳定，交流网络侧具有一定强度能够提高电压支撑能力，而当改变运行点为P2 时交流母线电压与直流功率发生崩溃，系统失稳.时域仿真结果与4.1 节中的数值计算结果对应.进一步通过仿真分析负荷特性与联络线导纳对电压稳定性的影响，在交流网络侧加装电动机负荷后，临界值λc由2.17增加到2.21，说明考虑电动机负荷会降低电网强度，而在增加恒阻抗负荷后，临界值 λc由2.17 减小为2.14，说明恒阻抗负荷能够提升系统强度[25]；增大混合直流三馈入系统中的联络线导纳b12，仿真结果表明，直流间的联络导纳越大，电网强度越强.

图7 混合直流馈入系统的时域仿真结果Fig.7 Time domain simulation of HMIDC system

4.3 IEEE-39 节点系统动态仿真

通过如图8 所示的IEEE-39 节点模型验证本研究强度指标的有效性，基于表3 的参数将LCCHVDC1 逆变侧在节点26 接入，VSC-HVDC 逆变侧在节点28 接入，在仿真中设置直流额定容量为100 MV·A，其余参数基准值与4.1 节一致.

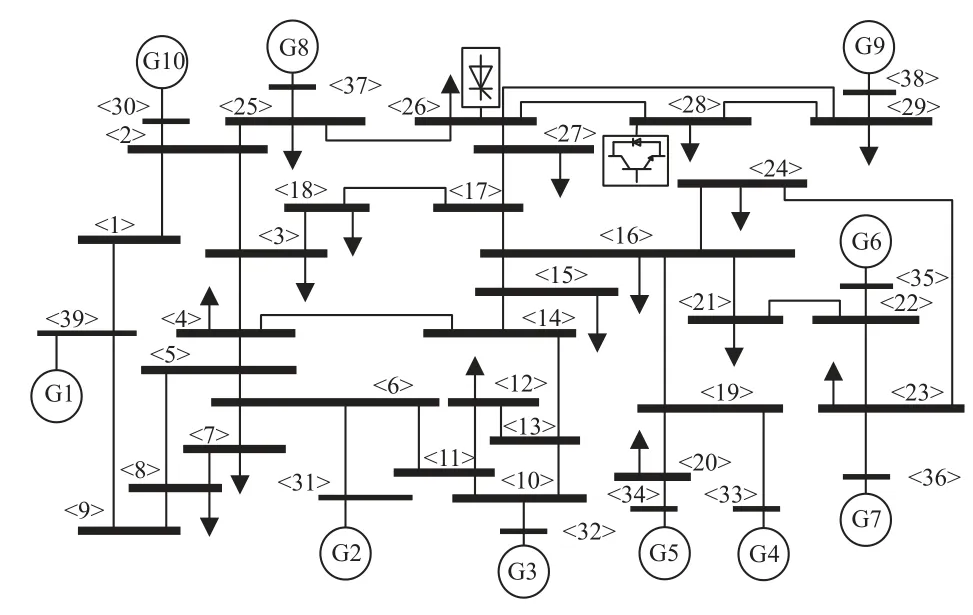
图8 IEEE-39 系统模型Fig.8 IEEE-39 system model

基于图3 给出的分析步骤通过数值计算得到LCC-HVDC1 的功率传输极限为1.81p.u.，对应的λc=2.07.在进行大系统时域仿真时，通过改变LCC-HVDC1 的功率参考值来改变系统强度，首先设置LCC-HVDC1 的初始运行点为P3，直流功率Pd1=1.73p.u.，对应的 λ1=2.14＞λc,系统具有一定的电压稳定裕度，该运行点下系统是稳定的.进一步，在2 s 时将运行点由P3 更改为P4，Pd1增加至1.84p.u.，此时 λ1=2.03＜ λc，系统在对应的电网强度下无法维持稳定运行，上述过程对应的时域仿真结果见图9.图中，Uac_bus26表示母线26 处的交流电压.

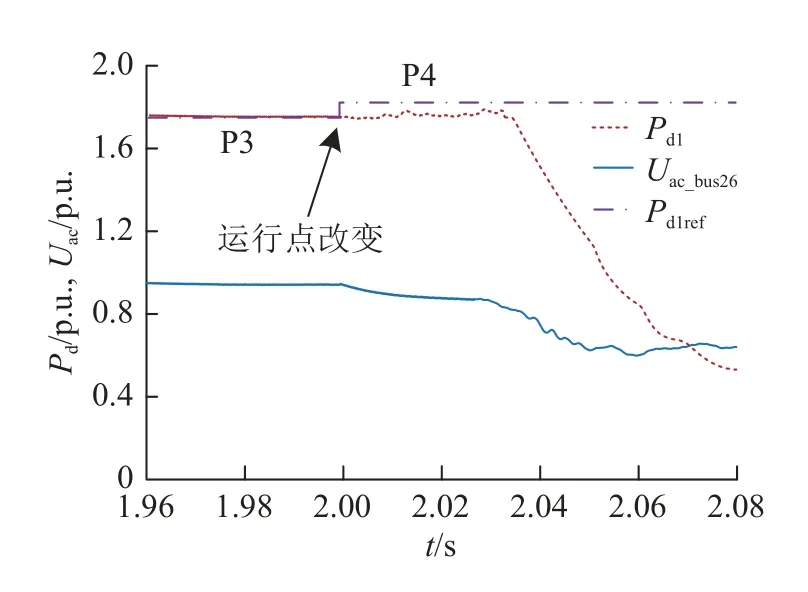
图9 IEEE-39 系统的时域仿真结果Fig.9 Time domain simulation of IEEE-39 system

5 结论

（1）LCC-HVDC 在CP-CEA 和CC-CEA 控制方式下会降低系统强度，恶化系统的电压稳定性，而在CP-CV 和CC-CV 控制下对系统电压稳定性有提升作用；

（2）VSC-HVDC 接入对系统电压稳定性的影响可以通过模态摄动近似分析，在进行混合直流多馈入系统强度分析时须综合考虑直流容量、联络导纳的影响，直流容量越小或联络导纳越大，电压稳定裕度越大.

所提方法旨在抓住混合直流馈入系统电压稳定性评估的主要矛盾，采取适合工程计算的思路，有助于促进网络模态解耦类强度指标在受端电网规划与运行中的应用.未来将进一步研究考虑负荷特性后模态解耦类电网强度评估指标的计算方法.