基于DFS 与蚁群算法的电弧增材复合路径规划算法优化

王瑞超，高祥，李会军，朱国崇，许健仪

(五邑大学，智能制造学部，广东 江门 529020)

0 前言

电弧增材制造（Wire and arc additive manufacturing,WAAM）是一种以电弧焊接技术为基础，基于三维数字化切片模型，采用逐层熔敷堆积原理，在基板上堆积出接近产品形状和尺寸要求的三维金属胚件的先进制造技术[1-3]，特别适用于中大型复杂结构金属部件的制造。电弧增材制造的路径规划方法是影响成形件的尺寸精度和成形效率的重要因素[4]。若路径规划不合理，可能会出现过多的弧坑塌陷、欠堆积和过堆积现象，导致成形尺寸精度低、表面成形不平整；增材过程中焊枪空行程过多，则会降低成形效率[5]。目前，电弧增材制造路径规划方法主要有zigzag 扫描、轮廓偏置扫描、螺旋扫描和分形扫描。其中zigzag扫描方法具有算法简单、路径连续性高，存在拐角较多、边缘台阶效应；轮廓偏置扫描方法具有边缘成形精度高，存在起弧熄弧次数较多，适应性差、存在干涉等；螺旋扫描方法具有路径连续性高，存在算法复杂、适应性差等；分形扫描方法具有路径连续性高，存在算法复杂、拐角多、边缘台阶效应。对于形状复杂的填充截面采用单一的路径规划方式，成形质量往往不能得到保证，而且成形效率较低。在权衡各种路径规划方法的优劣后，得出较好的路径规划方案是采用复合路径规划。而目前应用较多zigzag 扫描和轮廓偏置相结合的复合路径规划，即成形件的内外轮廓采用轮廓偏置填充，在轮廓偏置内采用zigzag 扫描填充[6-8]，其具有成形尺寸精度高、成形效率高、算法简单等优点。

采用zigzag 扫描与轮廓偏置相结合的复合路径规划方法，在此基础上，为了进一步提高成形效率，采用深度优先搜索算法对zigzag 扫描路径分区进行连接，减少zigzag 扫描路径的起弧熄弧次数，同时引入蚁群算法搜寻路径规划顺序和起弧点的最优组合，使总空行程长度最小。

1 复合路径规划方法

1.1 轮廓偏置路径

成形件的轮廓是由STL 格式的三维模型与切片平面相交而得，其由多条线段组成的封闭多边形。多边形的偏置向量正好位于其轮廓线内角的角平分线上，外轮廓的偏置向量方向指向其内部，而内轮廓则指向其外部。内外轮廓的偏置原理相同，仅偏置方向相反，下面以外轮廓为例进行说明。

假设外轮廓上有n个顶点pi(xi,yi)(i=1,2,3,···,n)，并进行逆时针排序，设pi的偏置点为，偏置间距为d，向量V1=pi-pi-1，向量V2=pi+1-pi，若V1×V2的值为正，则pi为凸顶点，否则pi为凹顶点。当pi为凸顶点时，根据几何关系[9]，则有

当pi为凹顶点时，根据几何关系，则有

由此可以求得pi点的偏置顶点连接外轮廓的每个偏置点便可得到轮廓偏置路径。对于内轮廓偏置，相反地，其顶点需要按照顺时针排序，若V1×V2的值为负，则pi为凸顶点，否则pi为凹顶点，同样通过式（1）～式（6）求解其偏置顶点。如果轮廓偏置的过程中出现干涉现象，可以采用轮廓连接合并与分解的方法进行消除[10]。为了避免干涉现象的产生，文中只求解一次内外轮廓偏置路径。

1.2 zigzag 扫描路径

上一节介绍了轮廓偏置路径的计算方法，获得轮廓偏置路径后使用zigzag 扫描路径对其内部进行填充。zigzag 扫描路径是由平行扫描路径连接而成的连续路径[11]，该算法基本实现步骤如下所述。

步骤1：设扫描线的间距为d′，求出轮廓偏置线的y坐标最大值ymax和最小值ymin，沿y轴负方向生成扫描线

步骤2：求扫描线与轮廓偏置线的交点，将交点按照x的坐标值从小到大进行排序，记录交点个数Ni，然后将交点存储到一个数组中。已知扫描线纵坐标为yi，设轮廓偏置多边形的相邻两顶点分别为pm(xm,ym)和pn(xn,yn)，求得交点横坐标x：

步骤3：当交点个数Ni发生变化时，则创建新数组存储新产生的交点，然后将各数组中同一条扫描线上的交点两两奇偶配对构成0.5Ni个扫描路径，再将同一条扫描线上的扫描路径进行分区，分区数目为0.5Ni，最后对所有分区进行排序。图1 为扫描路径的生成与分区示意图。

图1 扫描路径生成与分区示意图

步骤4：依次连接各数组中同一分区内y坐标值相邻的扫描路径的末端点和首端点，便可在该分区内生成一条连续的zigzag 扫描路径。

上述每条扫描线与轮廓偏置线交点数目Ni一直为偶数，但实际中根据不同的扫描间隔d′，扫描线可能会与轮廓偏置线顶点相交，使得交点数目为奇数；或者扫描线与某一段轮廓偏置线重合，在理论上会有无穷多个交点，实际上会导致步骤2 的式（8）无解，这2 种异常情况最终可能会导致步骤3 中生成错误的扫描路径和分区。若出现此类异常情况，将对异常轮廓线及异常交点进行删除处理[12]。

采用轮廓偏置路径和zigzag 扫描路径相结合的复合填充路径，图2 为单层截面轮廓的复合填充路径生成流程。需要注意的是，实际上内外轮廓需进行2次偏置运算。第一次偏置的目的是获得内外轮廓偏置路径，第二次偏置作为求解扫描线交点的依据。

图2 复合路径生成流程

2 zigzag 分区连接

根据zigzag 路径生成原理可知各分区之间zigzag扫描路径并不连续，故在每个分区内都需要重新起头，实际增材过程中则需重新起弧。显然，zigzag 扫描路径的分区越多，起弧和熄弧次数越多，空行程越多，既降低了表面成形质量，也降低了成形效率，同时也增加了起弧失败的风险。为了减少起弧熄弧次数，采用深度优先搜索（Deep first search,DFS）来尽可能连接各分区之间的扫描路径。

深度优先搜索算法是将最近刚产生的结点优先扩展，当达到一定的深度限制时，如果未找到目标或者无法再扩展，则回溯到前一个分叉结点继续扩展[13-14]。深度优先搜索过程，如图3 所示，图中箭头上的标号表示搜索的顺序。假定从分区1 开始搜索并标记分区1，若分区1 不是目标分区，则搜索与分区1 相邻且未访问的分区，此时满足的分区有分区2 和分区3，假定优先访问分区2 并标记分区2。若分区2 不是目标分区，则搜索与分区2 相邻且未访问的分区。重复以上操作，直至访问到分区5，由于2 是已访问的分区，所以此时分区5 已没有相邻且未访问的分区，则开始回溯搜索并判断前一分区是否存在其他相邻且未访问的分区，重复回溯搜索直至分区1，然后访问分区3，直至搜索分区6，遍历所有分区后结束搜索。深度优先搜索算法的基本操作步骤如下所述。

图3 分区深度优先搜索过程示意图

步骤1：建立所有分区的无向图G。

步骤2：选取某一分区Gi作为起始搜索分区，并标记该分区。

步骤3：以当前分区Gi进行扩展，搜索其邻近分区Gj，然后判断分区Gj是否被访问过，若Gj未被访问过，则标记Gj；若Gj已被访问过，则搜索Gi的其它邻近分区。

步骤4：根据步骤2 确定当前分区，并重复步骤2进行搜索。

步骤5：若当前结点的所有邻近分区都已被访问过，仍未找到目标分区，则回溯其前一分区，搜索该分区的其它邻近分区。

步骤6：重复步骤3～5 直至找到目标分区或者遍历所有分区为止。

文中设定两分区之间能够建立连接应满足的条件为：①两分区之间的相邻扫描路径规划方向相反；②两分区相邻扫描路径的端点在同一轮廓偏置线的同一侧且到该轮廓偏置线具有相同间隔；③两分区相邻扫描线端点y坐标的差值等于1 倍扫描间距，且两端点的距离不大于倍扫描间距，从而避免产生过小的拐角[15]。将“目标分区”设定为“与起始分区满足分区连接条件的分区”，若搜索不到目标分区，则返回起始分区的序号。zigzag 路径分区DFS 连接流程如图4 所示，若存在目标分区，两分区会合并为一，在下一次循环中以目标分区的序号参与搜索，而且作为起始分区进行填充时，会一次性连续填充，进而实现分区连接。

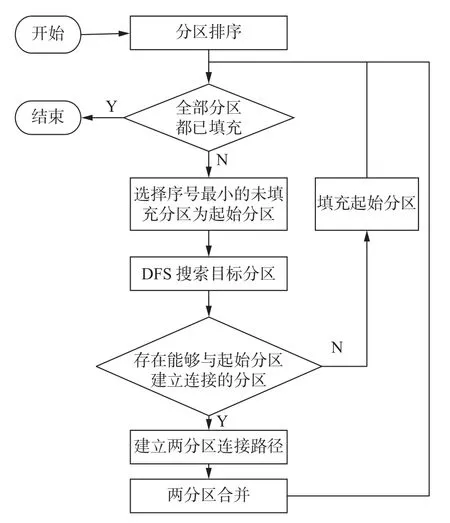
图4 zigzag 路径分区DFS 连接流程

3 复合路径空行程优化

空行程，即某一段路径熄弧点到下一段路径起弧点的水平距离，是影响电弧增材成形效率的重要因素。zigzag 分区连接在减少起弧熄弧次数，同时也能够在一定程度上减少空行程。此外，另一个直接影响空行程大小的因素是各区域路径规划顺序和起弧熄弧点的选择，这可以归为旅行商问题（Traveling salesman problem,TSP），即找到路径规划顺序和起弧熄弧点的最优组合，确定最优空行程路径，在保证焊接工艺稳定的前提下，使得每个区域只被填充一次且总空行程最短。蚁群算法最早应用于求解TSP，是目前解决组合优化问题最有效的工具之一[16]。对于复合填充路径，每条zigzag 的起弧熄弧点数量为2，而每条轮廓偏置路径的起弧熄弧点数量取决于轮廓的顶点数目。根据此特点，使用改进的蚁群算法搜索路径规划顺序和起弧熄弧点的最优组合，求解最小总空行程。该算法具体表述如下所述。

设填充路径区域的数量为n，区域i到区域j的距离为Dij，(i,j=1,2,3,···,n)，区域i有p个点，区域j有q个点，Dij的表达式如下

式中：dpq为区域i的第p个熄弧点到区域j第q个起弧点的距离。

设t时刻区域i到区域j之间路径上的信息素浓度为Tij(t)，(i,j=1,2,3,···,n)，Tij(t)的表达式如下

式中：τpq为区域i的第p个熄弧点到区域j第q个起弧点的路径上信息素浓度。设蚁群中蚂蚁的总数为m，t时刻蚂蚁k会从区域i访问区域j的概率为(k=1,2,3,···,n)，表达式如下

式中：ppq为t时刻蚂蚁k从区域i的第p个熄弧点访问区域j第q个起弧点的概率，ppq的求解式如下

式中：ηpq(t)为启发函数，表示区域i的第p个熄弧点到区域j第q个起弧点路径的能见度；ηpq(t)=1/dpq，α为信息素因子；β为启发函数因子；allowedk为蚂蚁k未访问过区域的集合。

当每只蚂蚁访问所有区域后，对所走路径上的信息素进行全面更新，信息素更新的表达式为

式中：ρ为信息素挥发因子；为第k只蚂蚁在区域i到区域j之间的路径上留下的信息素浓度的增量；Q为信息素常数；Lk为第k只蚂蚁走完所有区域后总的路径长度。蚁群算法的流程如图5 所示，该算法的具体操作步骤如下所述。

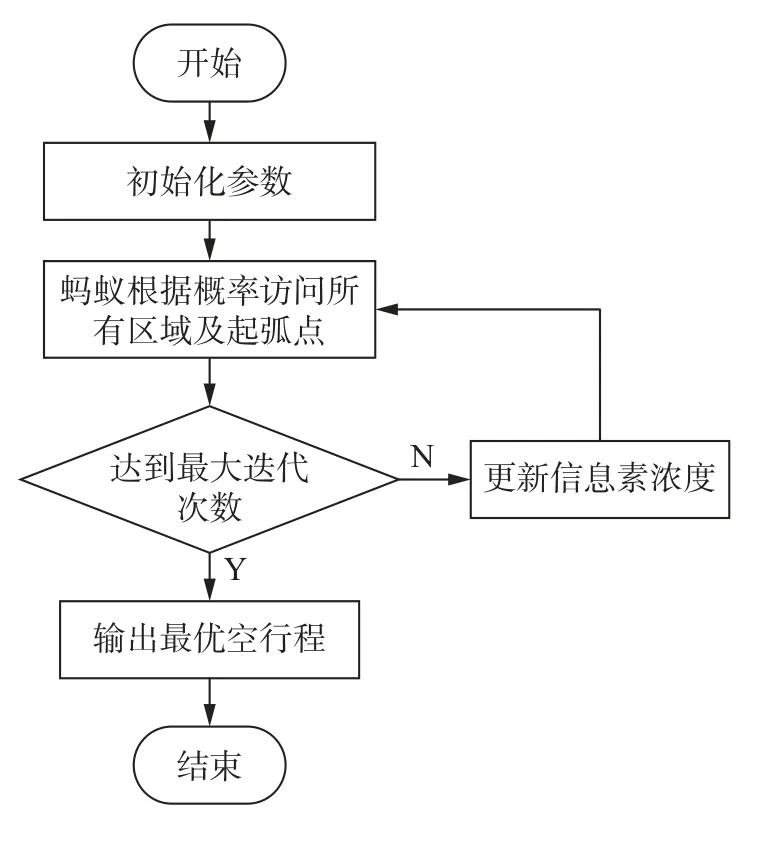
图5 蚁群算法流程

步骤1：输入区域点集并计算各区域之间熄弧点到起弧点的距离矩阵。

步骤2：初始化相关参数，包括蚂蚁数量m、信息素因子α、启发函数因子β、信息挥发因子ρ、信息素常数Q、最大迭代次数、初始信息素浓度T(0)。

步骤3：随机将m个蚂蚁放入不同区域的出发点，根据式（10）～式（12）计算每只蚂蚁从当前区域的熄弧点到下一区域起弧点的概率，然后根据概率确定每个蚂蚁下一个要访问的区域以及起弧点，同时更新allowedk，直到每只蚂蚁访问完所有区域。

步骤4：计算每个蚂蚁经过的路径长度Lk，记录本次迭代中最短路径距离，同时根据式（13）和式（14）更新每条路径上蚂蚁留下的信息素浓度。

步骤5：重复步骤3～4，直到达到最大迭代次数。

步骤6：输出最优路径对应的区域访问顺序、各区域的起弧熄弧点及最短空行程的长度。

4 算法验证与分析

为了验证上述算法的有效性，以图6a 的三维模型为填充对象，对其截面轮廓进行复合路径规划，首先，采用DFS 和蚁群算法先后对填充结果进行优化；然后，对优化结果进行对比分析。设置轮廓偏置间距为5 mm，zigzag 扫描间距为10 mm。为了充分测试DFS 算法连接zigzag 分区的性能，采用9 种不同扫描倾角zigzag 路径对图6b 的轮廓进行规划，如图7～图15 所示。各种扫描倾角的zigzag 分区经DFS 连接前后起弧熄弧点的对比结果如图16 所示，图中各轮廓偏置路径的起弧熄弧点已重合且数量固定为8。

图6 填充对象

图7 0°扫描倾角zigzag 分区连接前后对比

图9 45°扫描倾角zigzag 分区连接前后对比

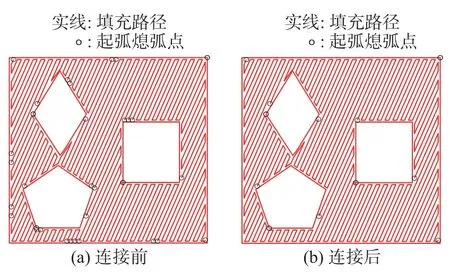
图10 67.5°扫描倾角zigzag 分区连接前后对比

图11 90°扫描倾角zigzag 分区连接前后对比

图13 135°扫描倾角zigzag 分区连接前后对比

图14 157.5°扫描倾角zigzag 分区连接前后对比

图15 180°扫描倾角zigzag 分区连接前后对比

分区连接前后的差异越大，则算法的优化效果越好，由图16 可知，当扫描倾角为0°，22.5°，45°，67.5°，180°时，DFS 分区连接算法优化效果最好，zigzag 路径条数与连接前相比减少了约71.4%，起弧熄弧点总数减少了约55.6%；当扫描倾角为112.5°时，算法优化效果最差，zigzag 路径条数与连接前相比减少了约55.6%，起弧熄弧点总数减少了约38.5%，原因是其分区连接前的zigzag 路径条数和起弧熄弧点总数相比其他情况最少。综上所述，对于图7～图15 的填充模型而言，DFS 分区连接算法对不同扫描倾角zigzag 分区皆能起到很好的连接作用。

设置蚁群算法的蚂蚁规模为30，信息素因子为2，启发函数因子为2，最大迭代次数为300。下面以0°扫描倾角的复合填充路径为例，测试蚁群算法优化空行程的性能，分区连接后的复合填充路径经蚁群算法寻优的最短空行程长度如图17 所示。复合填充路径寻优前后空行程路径对比如图18 所示。其中，图18c 外部矩形和内部菱形、五边形偏置路径的起弧熄弧点相比优化前已发生变化，总空行程路径长度对比结果见表1。根据表1 可得，DFS 与蚁群算法可以大大减少总空行程长度，具体表现为DFS 连接后的空行程长度相比优化前减少了约58.2%，在此基础上再经蚁群算法寻优后空行程长度又进一步减少了约26.9%。

表1 总空行程路径长度对比

图17 最短空行程长度

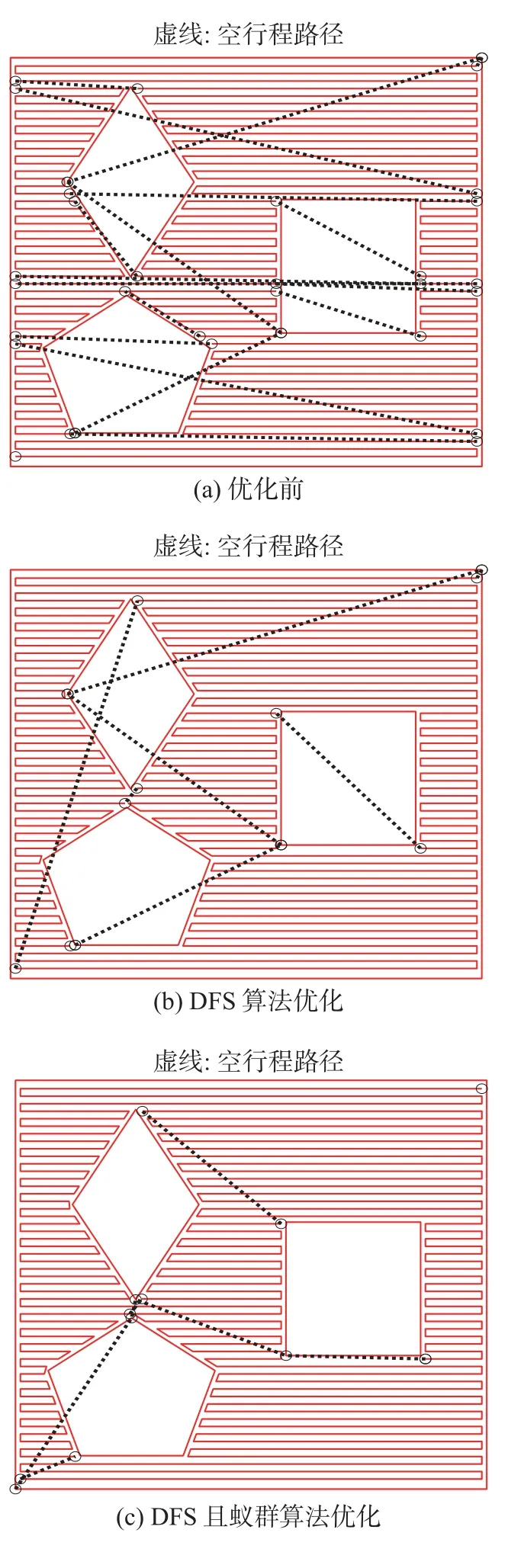
图18 空行程路径对比

5 结论

（1）实现了一种适用于复杂轮廓截面的电弧增材复合路径规划算法。

（2）提出了一种用于连接各分区zigzag 路径的DFS 分区连接算法，仿真结果表明：DFS 分区连接算法对不同扫描倾角的zigzag 路径能够起到良好的连接作用。

（3）采用蚁群算法优化分区已连接的复合路径总空行程，结果显示：在DFS 与蚁群算法共同作用下可以极大程度上减少总空行程长度，验证了算法的有效性和可行性，为下一步进行实际的电弧增材制造扫描算法优化提供了方法。