基于函数凹凸性命制的高考数学导数试题本质研究

严天珍

(甘肃省天水市第一中学,甘肃 天水 741000)

美国数学家哈尔莫斯(P.R.Halmos)曾说:问题是数学的心脏,数学的真正组成部分是问题和解[1];数学作为一门研究规律的学科,毫无疑问数学解题教学有其内在的属性和规律,而这个属性与规律就是数学解题的本质[2].

凹凸性是刻画连续函数性质的重要工具之一,不仅在高等数学中具有广泛的应用价值,同时也是高考数学试题命制的热点[3].回顾近年高考试题发现,基于函数凹凸性命制的高考数学试题频频出现,但由于普通高中数学课程标准并没有对函数的凹凸性做具体要求,相关性质在高中数学内容中又分布得较为隐蔽和零散,导致学生不会以整体的视野去统整相关的内容,更难将该思想方法顺利迁移到相关的解题中去.因此,函数凹凸性的“学考分离”现象成为高中数学教学和高考备考中一个不容忽视的问题.

为此,笔者从高中学生认知水平的前提出发,在介绍函数凹凸性相关定义和定理的基础上,对近年基于函数凹凸性的高考数学导数试题进行示例分析和解题本质研究,以期为一线教师的解题教学和高考备考提供参考和启示.

1 预备知识

定义设f(x)为定义在[a,b]上的连续函数,若对[a,b]中任意两点x1,x2和任意实数λ∈(0,1)总有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则称f(x)为[a,b]上的凸函数;反之,如果总有f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),则称f(x)为[a,b]上的凹函数.

定理[4]设f(x)为定义在[a,b]上的二阶可导函数,则在[a,b]上f(x)为凸(凹)函数的充要条件是f″(x)≥0(f″(x)≤0).

2 “ f(x)≤kx+b(或≥)”型导数试题的分析与结论

例1(2017年高考全国Ⅱ卷文科数学第21题)设函数f(x)=(1-x2)ex.

(1)讨论函数f(x)的单调性;

(2)当x≥0时,f(x)≤ax+1,求实数a的取值范围.

解析(1)略;(2)因为f(x)=(1-x2)ex,所以f′(x)=ex(-x2-2x+1),进而有f″(x)=-ex(x2+4x+1)<0在[0,+∞)上恒成立。由定理可知f(x)在[0,+∞)上为凹函数,又因为f(x)过点(0,1),所以f(x)在点(0,1)处的切线方程为y=x+1,因为f(x)为[0,+∞)上的凹函数,易知曲线y=f(x)总是在它的任一切线的下方,即f(x)≤x+1,又因为,当x≥0时f(x)≤ax+1,所以a的取值范围为[1,+∞).

评析含参不等式恒成立求参数取值范围的问题是高考中的热点,也是难点.解决的方法主要有分类讨论和分离参数,分类讨论由于分类标准的复杂多样往往不被一线师生所使用,而分离参数因其思想简单而易于被学生接收,但解题过程往往因为构造函数复杂、用到洛必达法则等困难而半途而废.因此在解决“f(x)≤kx+b型”函数问题时,利用函数的凹凸性并考虑相切的临界状态,无疑是一种简洁有效的办法.

结论1 设f(x)为定义在[a,b]上的二阶可导函数,对[a,b]中任意两点x,x0,则有:

(1)f(x)为[a,b]上的凸函数⟺f(x)≥f(x0)+f′(x0)(x-x0);

(2)f(x)为[a,b]上的凹函数⟺f(x)≤f(x0)+f′(x0)(x-x0).

不难理解,该定理的几何意义是:若f(x)为[a,b]上的凸函数,则曲线y=f(x)总是在它的任一切线的上方;若f(x)为[a,b]上的凹函数,则曲线y=f(x)总是在它的任一切线的下方.

回望近年高考,2018年高考全国Ⅰ卷文科数学第21(2)题、2018年高考全国Ⅲ卷文科数学第21(2)题、2019年高考全国Ⅱ卷理科数学第20(2)题、2019年高考全国Ⅱ卷理科数学第20(2)题、2020年高考全国Ⅰ卷文科数学第20(2)题、2020年高考全国Ⅱ卷文科数学第21(1)题等,都是基于函数凹凸性命制的,且均可以借助结论1的思想方法解答.限于篇幅,此处不再做示例分析.

例2 (2020年高考全国Ⅱ卷文科数学第21题)已知函数f(x)=2lnx+1[4].

(1)若f(x)≤2x+c,求c的取值范围;

构造m(x)=f′(x)(x-a)-[f(x)-f(a)],则m′(x)=f″(x)(x-a)

所以g(x)在(0,a)和(a,+∞)上是减函数.

结论2设f(x)为定义在[a,b]上的二阶可导函数,x0∈(a,b),则有:

例3 (2020年高考天津卷数学第20题)已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数.

(1)(第一问略);

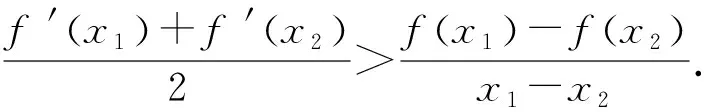
综上所述,可以得到如下结论:

结论3设f(x)为[a,b]上的三阶可导函数,x0∈[a,b],则有:

解题研究一直是中国数学教育研究的一个基本课题[5].解题不仅仅是给出试题的一种或几种解答,更应探求解题本质,即不断深究问题,参透题目本质,实现以题会类,真正把解题教学与“四基四能”的提升、核心素养的形成有机地统一起来.