局部换元法求解一类多元“根式和”问题
刘 波
(靖江市斜桥中学,江苏 靖江 215000)
下面举例说明局部换元法在求解竞赛中一类多元“根式和”问题的应用.
1 证明不等式

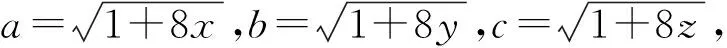
于是83=83·1=83·xyz=8x·8y·8z
=(a2-1)(b2-1)(c2-1)
=(a-1)(b-1)(c-1)(a+1)(b+1)(c+1)

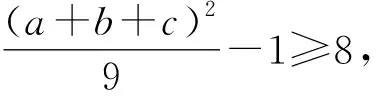
所以(a+b+c)2≥81.
因为a,b,c>1,所以a+b+c≥9.
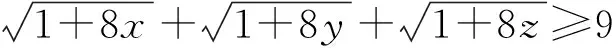
点评若本题直接证明,不仅有三个变量,而且目标式中含有三个“二次根式”,证明起来比较困难.这里进行局部换元,将“83=83·1”进行1的代换后代入得到关于引进的参数的式子,分解、组合并两度利用三元均值不等式求解的.求解本题的关键在于为什么由“83”来切入,这需要对题意有较强的分析、把控的能力.


所以由xy+yz+zx+2xyz=1,
得a2+b2+c2+2abc=1.
由柯西不等式,得
(a+b+c)2≤(12+12+12)(a2+b2+c2)
=3×(1-2abc)
=3-6abc,
所以(a+b+c)2+6abc-3≤0,
当且仅当a=b=c时取等号.
又由三元均值不等式,得
当且仅当a=b=c时取等号.

整理得2(a+b+c)3+9(a+b+c)2-27≤0,
所以2(a+b+c)3-3(a+b+c)2+12(a+b+c)2-18(a+b+c)+18(a+b+c)-27≤0,
所以化简得(a+b+c)2[2(a+b+c)-3]+6(a+b+c)[2(a+b+c)-3]+9[2(a+b+c)-3]≤0,
所以[2(a+b+c)-3][(a+b+c)2+6(a+b+c)+9]≤0,
即[2(a+b+c)-3](a+b+c+3)2≤0,

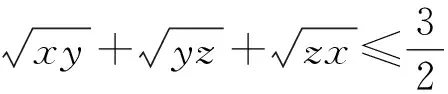
点评本题对目标式中的三个二次根式进行局部换元,转化后运用柯西不等式和三元均值不等式证明.在证明过程中,三次式“2(a+b+c)3+9(a+b+c)2-27”的分解是个难点,需要有较强的配凑、变形能力.
2 求最值
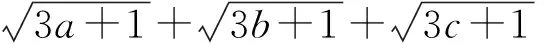

所以由a+b+c=1,得m2+n2+p2=6.
所以(m+n+p)2=m2+n2+p2+2mn+2np+2mp≤m2+n2+p2+m2+n2+n2+p2+m2+p2=3(m2+n2+p2)=18,


点评题由于a,b,c具有轮换性,其和为定值1,所以通过进行“局部换元”,进而结合重要不等式求解的.此解法别具一格,充分体现了“局部换元”法的应用价值和解题魅力.


由柯西不等式,得
(a+b+c)2≤(12+12+12)(a2+b2+c2)
=3×16=48,


点评若本题通过局部换元,运用柯西不等式求解,思路明朗、清晰,易于理解,同时也简化了运算.
3 求范围

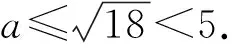
又因为0≤x,y,z≤1,
所以x≥x2,y≥y2,z≥z2,
于是3x+1≥x2+2x+1=(x+1)2,

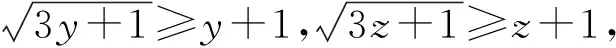


故[a]=4.
点评本题首先进行“局部换元”,进而结合重要不等式求得(上确界)上界,然后利用不等式性质得到下界从而得解的.


则由解法1,得a2+b2+c2=6.

构造二次函数
φ(λ)=(λ-a)2+(λ-b)2+(λ-c)2,
即φ(λ)=3λ2-2(a+b+c)λ+a2+b2+c2=3λ2-2Mλ+6.
因为φ(λ)≥0,对∀λ∈R恒成立,所以△=(-2M)2-4×3×6≤0,
从而M2≤18<25,






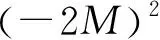



局部换元法作为一种常用的换元方法,其本质在于转化,其关键在于设元,其目的在于变换所研究的问题对象,达到化繁为简、化难为易之目的.通过上述几例可以看出,应用局部换元法解答某些竞赛题优势明显,在解题中应多体会这一方法.

