基于未确知测度的艰险隧道施工物资配置水平评估*

王景春,王 屹

(1.石家庄铁道大学 安全工程与应急管理学院,河北 石家庄 050043;2.石家庄铁道大学 土木工程学院,河北 石家庄 050043)

0 引言

随着我国隧道施工技术、设备的成熟,隧道建设不断向复杂艰险地区推进,同时也面临着恶劣气候、自然灾害等特殊自然环境。常常遇到Ⅳ、Ⅴ级围岩占比大,且隧道洞身穿越多条断层破碎带,存在突水突泥、大变形等多种不良地质的问题。为了保证现场施工的连续性、流畅性及安全性,需不断完善施工组织设计,而物资配置是其中的一项重要内容。混凝土、钢拱架、格栅、锚杆等是隧道建设中重要的施工物资,物资配置水平测度是对施工物资生产、运输、管理等方面连贯性、及时性的1项评估。

近年来,对于物资配置,多数学者注重于研究优化物资配置网络的方法,比如关键路径法[1-2]、基于BIM信息协同的方法[3]等。另外,应用数学工具建立单一问题的物资配置优化模型的研究也相对较多,比如Song等[4]、Yuan等[5]、尹静等[6]将机器学习与优化模型相结合,可高效地制定出物资配置计划。但是经过总结发现,国内外学者对物资配置水平的研究相对较少。但物资配置是一项系统工程,单一的优化模型不能满足物资配置的需要,分析物资配置的影响因素并进行水平测度,比较工区间配置水平优劣并相互借鉴也是提高工区物资配置水平的一种途径。另外,由于艰险地区隧道施工处于复杂特殊的自然环境中,物资配置的影响因素复杂多变,且存在相互耦合的关系,指标的选取具有不确定性、不完整性;再者,部分指标收集的数据精度难免不够。这决定了分析物资配置水平时的不确定性与模糊性较强,在进行水平测度时,很难利用简单的方法对其进行量化评价。目前,未确知测度理论已经应用于多个领域[7-9],对于处理影响因素众多及各因素传达的信息具有显著的不确定性和随机性的问题具有独特优势。故本文将采用该理论进行水平测度。

首先通过分析物资配置水平的影响因素建立评价指标体系,采用基于CRITIC修正G1组合赋权法确定其权重,进而构建未确知测度模型,最后将该模型应用于艰险地区3个在建隧道的4个工区中,通过对比分析表明其合理性和有效性,研究结果对艰险地区隧道施工物资配置水平的提高具有一定促进意义。

1 艰险地区隧道施工物资配置水平评价指标体系的构建

1.1 物资配置水平影响因素分析

艰险地区隧道施工物资配置水平影响因素分析是构建物资配置水平评价指标体系的前提。结合高海拔的地形条件和地震断裂带引起的突水突泥等特殊地质条件,借用全面质量管理理论中“人、机、环、管”的概念对物资配置水平影响因素进行分析。

1)“人”的因素。物资配置系统在正常运转的情况下,其差错往往出现在“人”的身上。一方面,员工经验不足,不能灵活处理各种突发事件;另一方面,以“师带徒”为一小组提高员工可靠性。

2)“机”的因素。包含但不限于“机器”的范围,主要指物资供应站(混凝土拌和站、钢结构加工厂)、运输车等的现实情况对物资配置的影响,比如机器故障、生产运作能力、运输能力等。

3)“环”的因素。包括自然环境、信息化环境和工作环境。地形条件、特殊地质条件、雨雪天气等自然环境因素,隧道洞内外信息交换水平等信息化环境,运输路径的通畅程度等隧道洞内外的工作环境均会降低工作人员和机器的工作效率及安全性,进而影响物资配置水平。

4)“管”的因素。不仅表示管理制度、物资配置流程的合理性等管理水平,还包括针对不同不良地质类型及不确定事件的预案的制定情况。

1.2 物资配置水平评价指标的筛选与分级

以现行标准为基础,现场调研我国艰险地区若干个隧道施工现场及物资配置实际情况,结合国内外相关文献进行总结分析。依据定量与定性相结合的设计原则,经过专家咨询确定艰险地区隧道施工物资配置水平评价指标,如表1所示。

表1 艰险地区隧道施工物资配置水平评价指标体系Table 1 Assessment index system for materials allocation level of tunnel construction in difficult areas

将艰险地区隧道施工物资配置水平划分为Ⅰ～Ⅴ共5个等级,依次表示水平从高到低,每一等级都有其量化数据范围。各定量指标均以实际情况采用实际数值进行赋值分级,对于定性指标X21、X22、X34、X35、X36,以现场管理人员和专家意见为基础[10]采用半定量化的方法取5、4、3、2、1这5个得分值,如表2所示。

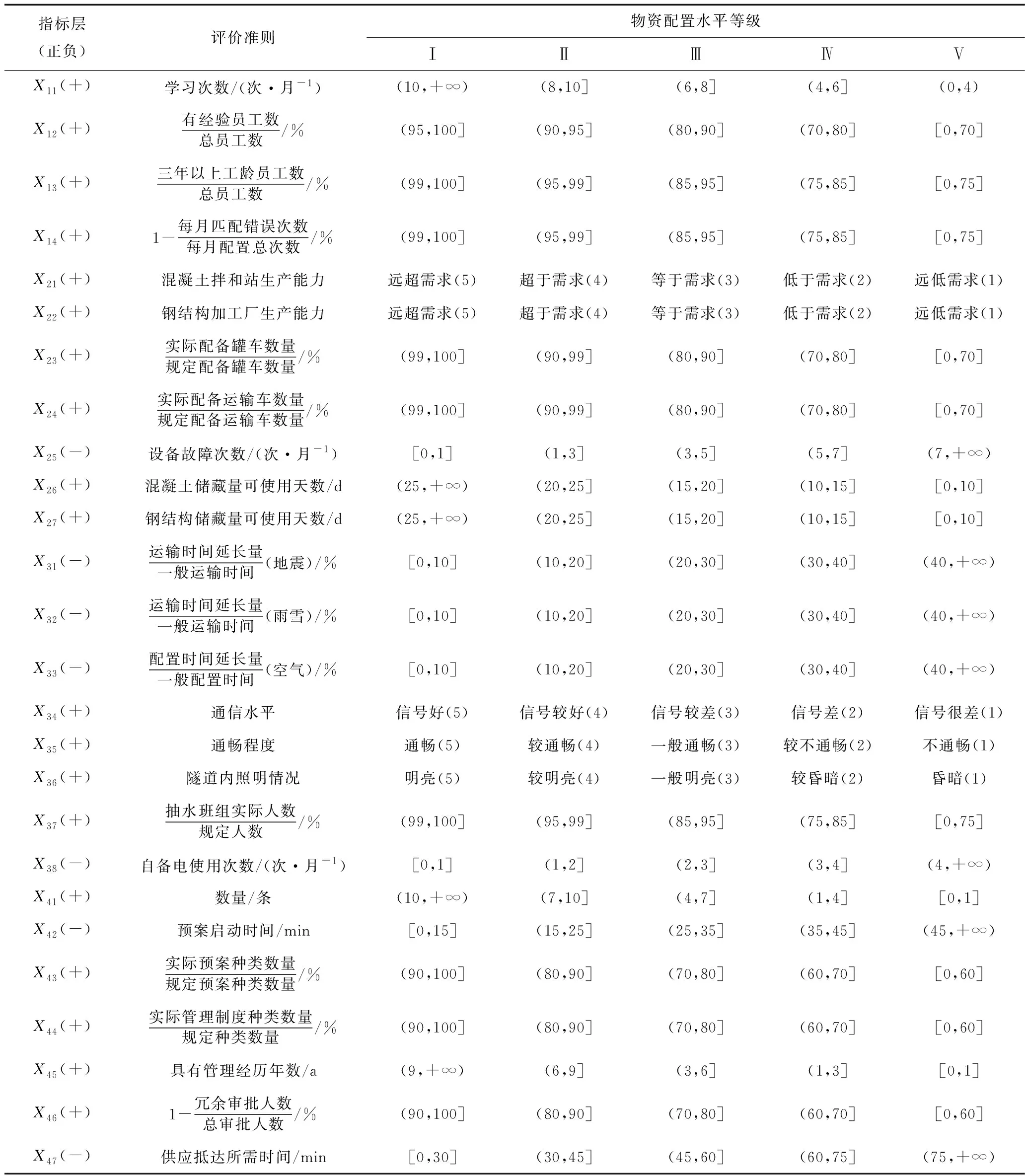
表2 艰险地区隧道施工物资配置水平评价指标分级准则Table 2 Grading criteria of assessment indexes for materials allocation level of tunnel construction in difficult areas

2 组合赋权-未确知测度模型

2.1 CRITIC修正G1法确定评价指标权重

CRITIC法是Diakoulaki等[11]于1995年提出的,该方法考虑了评价指标间的关系,通过标准差与相关系数确定权重,兼顾指标的对比度和冲突性[12],是1种优于熵权法的客观赋权方法[13]。同时,G1法是由AHP法优化改进而来[14]。

组合赋权常采用加法合成[15]和乘法合成[16]这2种方法进行主客观权重的组合,2种方法均具有一定的缺点。乘法合成法一是会产生指标权重的“倍增效应”,二是很难解释指标权重相乘的含义是什么。而加法合成法研究较多,一般通过求解优化模型对主客观权重进行分配,虽然具有一定的合理性,但仍然无法改变权重的组合模式,需要强化的指标不能强化,需要弱化的指标不能弱化。

因此,采用CRITIC修正G1主观赋权法,从指标层对指标权重进行组合。改进的G1法避免在确定相对重要性时的随机性和主观性问题,兼顾主观专家意见和客观数据信息。具体步骤如下:

1)评价指标的重要性排序,如式(1)所示:

(1)

式中:Xi为第i个准则层,i=1,2,…,a;Xij为第i个准则层下第j个指标,j=1,2,…,b。

2)CRITIC确定指标权重,如式(2)～(6)所示:

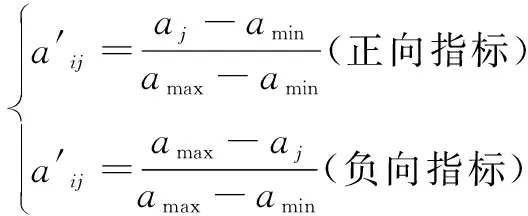
(2)

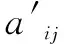
相关系数:

(3)

式中:Cov(i,j)为指标i,j的协方差;vari,varj分别为指标i,j的方差。

(4)

式中:m为指标个数;rij为相关系数。

(5)

式中:σj为指标j的标准差;Rj为指标j的冲突性。

客观权重:

(6)

式中:Dj为指标j的信息量。

3)基于CRITIC权重的指标层相邻指标重要程度sj,如式(7)所示,相邻准则层之间的重要程度同理。

(7)

式中:vj为指标j的客观权重。

一方面,在实际的应用过程中,相邻指标之间的重要程度可能会出现小于1的情况,显然与G1法的运算过程冲突。传统的做法是将相对重要性尺度设为1,即2个相邻的指标同样重要,但是由于指标之间存在明显的顺序关系,与实际的关系不一致;另一方面,在运算过程中还可能出现相邻指标之间CRITIC权重值之比过大,导致排名靠前的指标与靠后的指标最终权重相差数十倍[17]。所以可以用如式(8)所示的方法改进:

(8)

式中:vj为指标j的客观权重。

4)确定组合权重,如式(9)～(10)所示:

(9)

逆向递推:wj-1=sjwj

(10)

式中:wj为指标j的组合权重;sj为指标层相邻指标间的重要程度,j=b,b-1,…,2。

同理可得准则层权重。最终指标权重由指标层对于准则层权重与各准则层权重相乘可得。

2.2 未确知测度模型

设待评价方案F={F1,F2,…,Fn},评价指标X={X1,X2,…,Xm}。令研究空间为D={D1,D2,…,Dp},表示评价方案i关于评价指标j有p个评价等级,可用xij表示评价方案i关于评价指标j的实测值。Dk>Dk+1表示前一评价等级比后一等级配置水平高。

1)单指标未确知测度

根据实际情况,现采用运用最广泛的直线型测度函数,对数据进行测度,如式(11)所示:

(11)

式中:ui(x)为单指标未确知测度;x为实测值;ai为第i个评价等级的边界值,根据分级标准确定。

根据上述单指标未确知测度函数,可得待评价方案Fi的各项评价指标Xj的测度值uijk,进而可得单指标测度评价矩阵,如式(12)所示:

(12)

式中:uijk为待评价方案i的各项评价指标Xj的测度值,j=1,2,…,m;k=1,2,…,p。

2)多指标综合测度

向量uik=(ui1,ui2,…,uip)为方案Fi的多指标综合测度评价向量,如式(13)所示:

(13)

式中:uik为方案Fi的多指标综合测度评价向量;wj为指标j的组合权重;uijk为待评价方案i的各项评价指标Xj的测度值。

3)置信度判别

由于{D1,D2,…,Dp}为评价空间D的一个有序分割级,故引入置信度λ∈[0.5,1],如式(14)所示,令

(14)

式中:k0为第k0个评价等级Dk0;λ为置信度。则可认为样本Fi属于第k0个评价等级Dk0。

4)水平排序

引入式(15)进行方案间物资配置水平的排序[18]。对于水平等级{D1,D2,…,Dp},若D1>D2>…>Dp,则赋值I1>I2>…>Ip,且如式(15)所示:

(15)

式中:Ei为方案Fi的重要度,重要度越大可认为方案水平越高;Ik为水平等级Dk的赋值;uik为综合测度向量。

3 案例分析

3.1 数据来源

以艰险地区某3个在建隧道的4个工区(F1、F2、F3、F4)作为评价对象F,其具有相似的特殊地质条件和恶劣的气候环境,施工环境极其相似。现为了提高工区的物资配置水平,将各工区的物资配置方案评级比对,以找寻交流学习的方向。根据现场调研得到样本数据,如表3所示。

3.2 艰险地区隧道施工物资配置水平评估

1)指标体系组合赋权

由式(1)～(10)可知,主客观交叉混合赋权方法可求得各评价指标的权重,如图1所示。

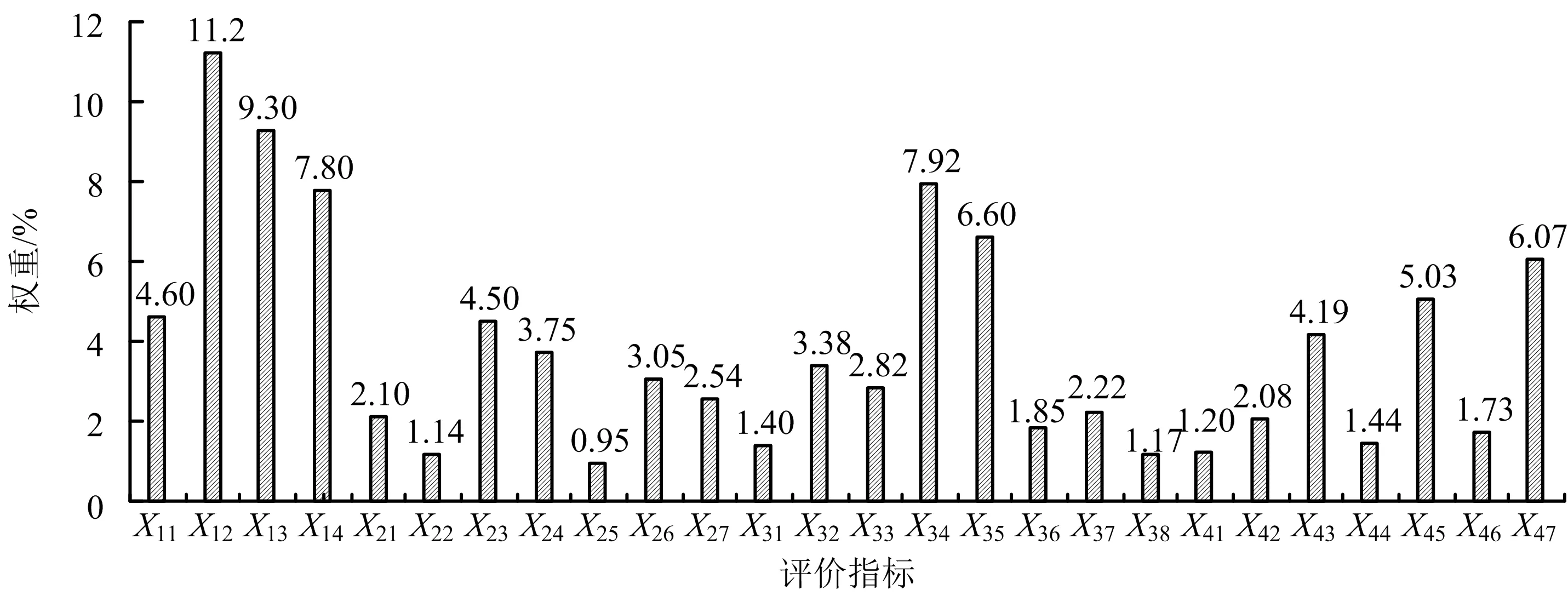
图1 各评价指标权重Fig.1 Weights of each assessment index

2)单指标测度矩阵

由于篇幅限制,仅列出样本工区F1相关计算结果,根据实测数据和测度函数计算其单指标测度矩阵,如式(16)所示。

(u1jk)26×5=

(16)

3)多指标测度向量与置信度判别

由本文方法所得的组合权重和式(13)、式(16)可计算得出工区F1的多指标测度向量u1k=(0.226 5,0.127 5,0.367 0,0.269 5,0.009 5),取置信度λ=0.5,根据式(14)从2个方向进行判别,则从小到大有k0=0.009 5+0.269 5+0.367 0=0.646 0>0.5,从大到小有k0=0.226 5+0.127 5+0.367 0=0.721 0>0.5,2次判定结果均为Ⅲ级。同理可得工区F2、F3、F4的隶属等级,如表4所示。可知工区F1、F2的物资配置水平为Ⅲ级,F3、F4为Ⅱ级。

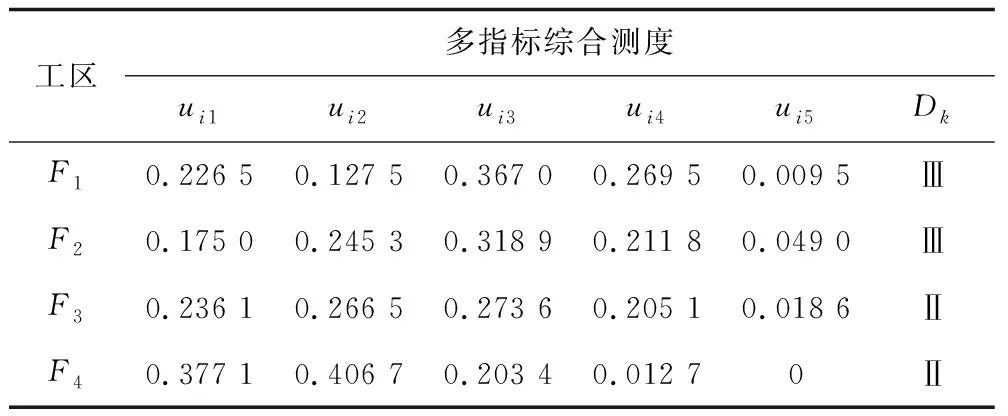
表4 置信度判别Table 4 Confidence determination

4)物资配置水平排序

由于D1>D2>D3>D4>D5,故令D1、D2、D3、D4、D5分别赋值为5,4,3,2,1。由式(15)可知样本F1、F2、F3、F4的重要度分别为3.292 1,3.285 4,3.496 4,4.148 2,即E4>E3>E1>E2,表明工区F4的物资配置水平最高,F3次之。因此,其他工区可借鉴工区F4的经验,以达到更高的物资配置水平。

3.3 结果与讨论

为了验证改进的赋权方法的准确性和可信度,将本文构建的基于CRITIC修正的G1法与常规的G1-CRITIC组合赋权法[16]、应用广泛的AHP-熵权组合赋权法[19]相比较,过程中的评级及优劣排序均采用未确知测度理论,结果如表5～6所示。

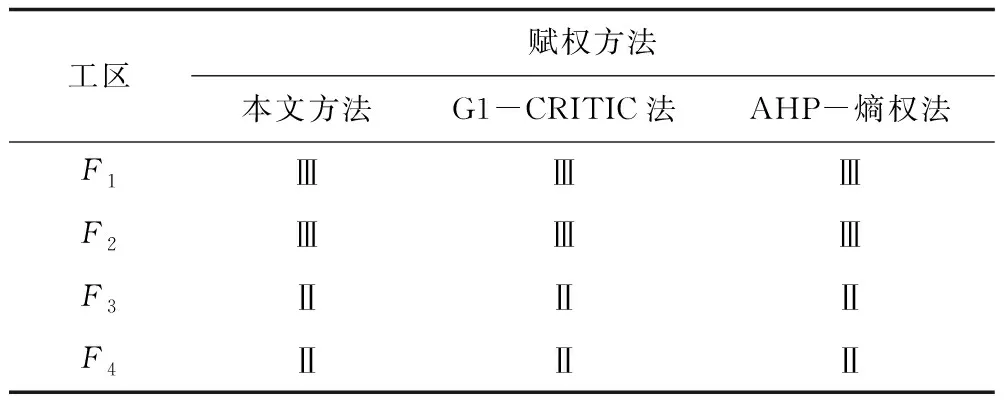
表5 配置水平评价结果Table 5 Assessment results of allocation levels

表6 配置水平优劣排序Table 6 Ranking of allocation levels

引起排序差异的主要原因一方面是AHP-熵权组合赋权法在运用AHP确定指标的主观权重时采用“1～9标度法”来描述指标间的重要程度,虽然这种方法本身具有科学性和有效性,但在实践中往往会产生指标主观权重相差数倍的结果,而这一点在本文和文献[16]中均得到解决,而且主客观权重的组合采用乘法合成法,产生了权重“倍增效应”,从而导致“经验人员比例”X12、“员工可靠性”X13权重过高;另一方面,F1、F2这2个工区本就属于同一在建隧道,所处客观环境比较相似,物资配置水平相当。

虽然以AHP-熵权组合赋权法为基础计算得出的4个工区的重要度标准差最大(即评价对象的区分度更高),但由于其权重计算的本身弊端明显,故而相比之下以本文提出的权重计算方法为基础的评价模型是三者当中最优的。

综上所述,本文构建的基于CRITIC修正G1主客观组合赋权方法具有准确性和有效性。首先,对于G1-CRITIC法而言,解决了主客观权重的组合方式无法合理选择的问题;其次,对于AHP-熵权法,改进了“1～9标度法”,也避免了主客观权重组合模式的选择,可有效避免因指标权重偏差过大造成的水平测度不准确现象的发生。同时结合未确知测度理论进行的物资配置水平的分级和优劣排序对于评价对象的区分度最高,且与现场实际及调研结果相符,其结果可为各工区提供相互学习交流的方向。

4 结论

1)针对艰险地区隧道施工物资配置本身的不确定性和信息的未确知性,从“人、机、环、管”4个方面构建包含4个准则、26项评价指标的评价体系,并将其划分为5个水平等级,为物资配置水平的测度提供一定的基础。

2)提出基于CRITIC修正G1组合赋权法,解决现有大部分研究因主客观权重的组合模式而导致的偏差现象,并兼顾专家主观意见和指标客观信息。

3)基于未确知测度理论建立隧道施工物资配置水平评价模型,以艰险地区的3个隧道的4个工区为例进行物资配置水平测度和优劣排序,结果为E4>E3>E1>E2,与现场调研和论证结果相吻合,可为艰险地区隧道施工物资配置提供一定的理论基础,有助于明确各工区的改进方向。