楼梯内单向下楼疏散及双向疏散的实验研究
于佳桐,高 瑾,龚景海
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.上海交通大学 航空航天学院,上海 200240)
0 引言
楼梯作为高层建筑关键的竖向逃生通道,承担着保证建筑内人员安全疏散至地面或其他安全位置的作用。由于楼梯内空间狭窄陡峭、人员密集,相较水平通道更容易发生人员踩踏等安全事故;同时,楼梯内人员的运动模式和水平通道存在明显差别。因此,在高层建筑已普遍存在的背景之下,有必要针对楼梯内人员疏散特征开展实验研究。
针对人员在多层、高层建筑楼梯上的宏观疏散行为,Peacock等[1]研究性别、是否携带物品、是否使用扶手、反应时间以及人员密度等8种因素对多层建筑人员下楼疏散速度的影响;Chen等[2]研究人员在高层建筑楼梯上楼疏散时速度随楼层变化的规律;Xu等[3]、Huang等[4]研究人员预期疏散距离以及疲劳因素对于疏散速度的影响;Zeng等[5]、Chen等[6]、王一等[7]研究环境照度及能见度与高层建筑楼梯中人员运动速度的关系。
汇流是高层楼梯中的常见疏散行为,Chen等[8]指出汇流会显著降低人员在楼梯中上楼、下楼的速度。然而,现有研究针对人员汇流行为的研究仍十分匮乏。在此背景下,本文开展1项高层建筑楼梯单向下楼疏散实验。该实验共包含有汇流和无汇流2个工况。通过比较每个工况内不同楼层所对应的速度、流率数据以及2工况间实验结果的差异,分析人员速度和流率随楼层变化的规律以及汇流对于其影响。
无论是正常情况还是紧急情况,楼梯内均有可能出现上楼、下楼人员相互对冲的不利情形。例如,正常使用的高校教学楼,课间时段由于上课学生和下课学生同时涌入楼梯,上下楼人群将以较高密度相向运动。类似的情况亦常出现在地铁车站、旅游景区、文体会展场所等公共建筑中。房屋建筑发生火灾时,会出现在建筑使用者逃生下楼的同时,消防人员上楼救援的情形。Gao等[9]提出楼梯内双向疏散的人员常表现出排队行为及互斥行为,并存在满载与交错2种移动模式;Ye等[10]的双向人流实验表明当上下楼人员比例为1∶1时人员的移动速度和流率将达到最小值,且此时将出现严重的人员对冲。目前针对房屋建筑内楼梯双向人员疏散的研究十分有限。为弥补此方面的不足,本文开展双向对流疏散实验,从而揭示不同运动模式下,人员上下楼的速度、流率与上下楼人员比例之间的关系。实验在Ye等[11]提出的正常步行、快速步行2种运动模式工况之外,额外设置跑步行进的工况。其中,正常步行工况旨在反映人员在日常情形中的运动状态,快速步行和跑步行进则对应人员在紧急疏散中的运动状态。实验共涉及9种上下楼人员比例,每种对流比例下包含上述3种运动模式工况。所有工况中实验人员总数均相同。
综上,本文基于某高层办公建筑楼梯开展单向及双向疏散实验,分析单向疏散中的汇流现象及双向疏散中上下楼人员比例对于人员速度、流率的影响,以期为多高层建筑人员疏散管理提供理论支撑。
1 实验场景设置
1.1 楼梯疏散场景
本文实验的地点位于上海交通大学某10层办公楼的楼梯间。该楼梯为高层建筑中常见的双跑楼梯,楼梯间的剖面图和平面图如图1所示。1层至2层、2层至3层每个梯段有15个踏步,3层至4层及以上楼层每个梯段有12个踏步。单个踏步高h=160 mm,进深d=260 mm,楼梯坡度θ=31.6°。台阶总宽度w=1 360 mm,从墙壁到扶手内侧边缘的净宽度w0=1 200 mm,各楼层楼梯入口门宽wd=900 mm。每层平台处安装有1部摄像头,以记录疏散过程中人员的实时动态,用于提取实验数据。

图1 楼梯尺寸Fig.1 Dimensions of stairs
实验共招募48名志愿者,包括22名女性、26名男性,全部为在读本科或硕士学生,身体健康无行动障碍,能够积极配合疏散实验工作。实验前通过招募问卷向志愿者说明实验时间、地点及目的,所有志愿者自愿参与实验。实验过程中,志愿者身穿胸部和背部均标有编号的服装,头戴红色或黄色安全帽,以便手动提取数据时予以识别。
1.2 高层建筑楼梯单向下楼疏散实验
本部分的实验于1~10层的楼梯开展。人员等候区被设置在7~10各楼层楼梯入口外侧电梯间内。
在有汇流工况中,由于在日常状态下本楼栋10,9,8,7层的人数依次递减,为尽量还原真实疏散情境,分别安排5,11,14,18名志愿者分布于7,8,9,10层等候区。工作人员吹响哨声下达疏散命令后,10层的志愿者立刻进入楼梯间下楼疏散。当发现有下楼疏散的志愿者经过9层平台时,9层等候区内的志愿者随即进入楼梯间下楼疏散。8层,7层同理,直至所有志愿者疏散至1层的指定位置。
在无汇流工况中,全部48名志愿者均被安排至10层的等候区。当工作人员下达疏散指令后,所有人员立即进入楼梯间下楼疏散至1层指定位置。
实验中志愿者应尽可能地快速运动,以模拟紧急情况下人员疏散特征。实验场景如图2所示。

图2 单向下楼疏散实验场景Fig.2 Experimental scene of one-way downstairs evacuation
1.3 单层楼梯双向疏散实验
本部分实验于4~5层的楼梯开展,在4,5层楼梯入口外侧电梯间内设置人员等候区。实验包括正常步行、快速步行和跑步3种运动模式以及9种对流比例工况。实验工况设置如表1所示,其中对流比例R的定义为上楼人数(nascend)与总人数(ntotal)的比值,如式(1)所示:

表1 双向疏散实验工况设置Table 1 Conditions setting of two-way evacuation experiments
(1)
上楼和下楼的疏散志愿者分别分布在4层和5层的等候区。每个工况中,2组人员接收到疏散命令时,同时向对方楼层开始疏散,直至所有人员疏散至对方楼层。实验场景如图3所示。

图3 双向疏散实验场景Fig.3 Experimental scene of two-way evacuation
2 实验数据来源
2.1 人员的运动速度
人员在1个梯段、平台或1个楼层内的平均运动速度如式(2)~(3)所示:
(2)
T=tend-tstart
(3)
式中:v为平均运动速度,m/s;L为人员在目标区段的移动距离,mm;T为人员通过1个梯段、平台或1个楼层的总时间,s;tstart,tend分别为目标人员进入和离开目标区段的时刻,s。tstrat和tend可通过逐帧分析实验视频获得,可精确至1/30 s,即视频1帧的长度。
对于1个梯段,Ltread如式(4)所示:
(4)
式中:N为1个梯段的总踏步数量,其中1~2层、2~3层N=15,3~4层、4~10层N=12。
由此,可计算出Ltread=4 837 mm(1~2层、2~3层)或Ltread=3 870 mm(3~4层、4~10层)。
针对平台上的人员移动距离,存在着多种假设及对应的计算方法[12]。本文采用目前相关研究中广泛认可的弧形运动轨迹假设,如式(5)所示:
Llanding=πr
(5)
式中:Llanding表示人员在中间平台上移动的距离,mm;r为疏散路线的半径,mm。
在单向疏散实验中,r=b/4,其中b为平台的宽度[2,8,12],本文实验中b=2 780 mm。在双向疏散实验中,由于人员具有靠右行走的习惯,上楼人员大多靠近楼梯扶手通行,而下楼人员大多远离楼梯扶手,如图3所示。因此有必要分别计算上楼、下楼人员的移动距离。本文假设上楼人员从梯段内侧4分点进入、离开平台,下楼人员从外侧4分点进入、离开平台,即对于上楼人员r=b/8,下楼人员r=3b/8。由此可以计算出单向疏散工况中Llanding=2 183 mm;双向疏散工况中上楼人员Llanding=1 090 mm,下楼人员Llanding=3 269 mm。
在单向下楼疏散实验中,除2~1层仅包含2个梯段及1个平台以外,每个楼层均包含2个梯段及2个平台。由于上下2梯段的长度不等,3层平台处将额外多出1段额外的步行距离Ladditional=540 mm,如图1(c)所示。疏散人员在各楼层的移动距离如表2所示。

表2 各楼层的移动距离Table 2 Moving distance of each floor
2.2 流率
流率f(单位:人·s-1)表示单位时间内通过某一断面的人员数量,可以衡量特定疏散工况中楼梯的通行能力。当待疏散的总人数一定时,疏散终点断面的流率越大,则代表所需要的疏散时间越短。流率f计算如式(6)所示:
(6)
式中:tfirst,tlast分别为第1个和最后1个人员通过目标断面的时刻,s;n为在这段时间内通过该断面的总人数。在双向疏散实验中,上楼人员和下楼人员的通行流率须分开统计。
3 单向下楼疏散实验结果分析
图4为有汇流和无汇流2种工况下,志愿者通过各楼层的速度分布。无汇流工况中,志愿者由10层疏散至7层的过程中,平均速度逐楼层加快。而后,平均速度呈现出逐楼层下降趋势。由《SFPE消防工程师手册》[13]及现有研究[8,11,14-16]提出的人员速度-密度基本图可知,人员在楼梯上的移动速度与人员密度呈负相关。无汇流工况中,在10~7层的疏散过程中,随着人流逐渐分散,楼梯上的人员密度逐渐降低,志愿者的平均速度得以加快。此外,由于志愿者需要一定的时间和距离由静止加速至期望速度,10~9层的平均速度小于后续的9~8层和8~7层。在7层以后,因为志愿者开始出现疲劳,平均速度呈现出下降趋势。这和Chen等[2]开展的20层楼梯单向上楼疏散实验中,人员因疲劳导致速度逐层下降的现象相互吻合。志愿者在整个疏散过程中的速度为(1.06±0.16) m/s(平均值±标准差,下同)。

图4 各楼层速度箱型图Fig.4 Velocity box diagram of each floor
有汇流工况的速度变化趋势较无汇流更加复杂。10~9层由于人员密度相对较低,且尚未出现汇流,平均速度达到1个相对较大值。从9层开始,由于各楼层等候区内的人员不断汇入楼梯,导致楼梯内的人员密度增大,平均速度较10~9层出现明显的下降,并一直持续到5层。5层之后,因为人员已经充分分散,5~4层的平均速度快速增长,甚至超过10~9层的数值,说明此时汇流的影响已不显著。4~1层则因为人员的疲劳,平均速度又呈现出逐层下降的趋势。志愿者在整个疏散过程中的速度为(0.99±0.12) m/s,较无汇流工况下降6.60%。
各楼层平台的流率数据如图5所示。无汇流工况中,随着疏散的进行,人员逐渐分散,各楼层的流率逐渐下降。有汇流工况中,9层因为有多达14名志愿者汇入楼梯间,使得人员流率在9层平台出现激增;在8层和7层汇入人员相对较少,且楼梯间内的人员已经有所分散,8层之后人员流率一直保持下降趋势。且总体而言,除10层无汇流工况的人员流率较高以外,其余楼层有汇流工况的流率均显著大于无汇流工况。
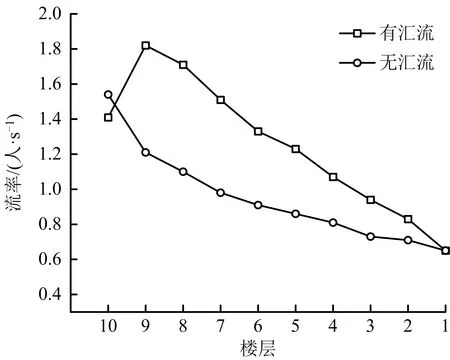
图5 各楼层的流率Fig.5 Flow rate of each floor
图6为7层平台处人员速度-密度基本图,数据点涵盖有汇流、无汇流2种工况。人员密度d的最小值、最大值分别为0.33人/m2和1.65人/m2。通过线性回归分析得到速度-密度函数为v=-0.395d+1.572。
4 双向疏散实验结果分析
4.1 梯段的局部疏散速度
上梯段是指从5层至4~5层中间平台,下梯段是指从4~5层中间平台至4层。图7中散点显示各工况下志愿者在上梯段和下梯段的疏散速度。当对流比例、运动模式相同时,上楼人员的平均速度普遍低于下楼人员。随着对流比例的变化,梯段上人员的运动速度变化不明显。

图7 梯段部分人员平均速度-对流比例关系Fig.7 Relationship between average speed and convection ratio of partial personnel on stairs
在Ye等[10]的楼梯双向疏散实验中,人员的运动速度呈现出随对流比例增加先减慢后加快的趋势,当对流比例为0.5时人员速度最低。因此,本文选择使用二次函数拟合速度与对流比例的关系,拟合结果如图7中曲线和表3~4所示。除下梯段正常步行下楼和跑步上楼工况以外,其余所有工况的相关指数均不足0.5,部分工况甚至不足0.1。这说明上下两梯段人员的速度受对流比例的影响十分有限。

表3 上梯段人员平均速度与对流比例的拟合方程Table 3 Fitting equation of average speed and convection ratio of personnel on upstairs section

表4 下梯段人员平均速度与对流比例的拟合方程Table 4 Fitting equation of average speed and convection ratio of personnel on downstairs section
4.2 平台的局部疏散速度
图8中散点显示各个工况下志愿者在中间平台处的平均速度。在平台上,人员的速度仍呈现出上楼小于下楼的规律;同样地,使用二次函数拟合速度-对流比例关系,可发现平台上人员平均速度与对流比例的相关性较上下两梯段更为显著,拟合结果如图8中曲线及表5所示。各工况拟合方程的相关指数均超过0.5,说明二次函数可以很好地描绘平台上速度与对流比例的关系。

表5 平台部分人员平均速度与对流比例的拟合方程Table 5 Fitting equation of average speed and convection ratio of partial personnel on platform
在拟合方程中,当速度v达到极小值时,记此时的对流比例为R0。由表5可知,6种运动模式所对应的R0处于[0.596,0.756]区间内,此时所对应的上楼人数为下楼人数的1.48~3.10倍。同时,本文发现无论上楼还是下楼,从正常步行、快速步行到跑步,R0均呈现出逐渐增大的趋势;相同运动模式下,上楼所对应的R0全部大于下楼。由此得出结论,“上楼人数的绝对占比”和“上下楼人数的均等程度”同时影响着疏散人员在平台上的速度,前者对快速运动及上楼的人员影响较显著,后者对慢速运动及下楼的人员影响较显著。
4.3 人员流率
图9中散点描述不同对流比例下各种速度工况的人员流率数据,选取的统计断面均为疏散的终点(上楼人员为上梯段顶端,下楼人员为下梯段底端)。通过对图9中散点进行二次函数拟合,结果如图9中曲线及表6所示,此时R0′为方程中流率f取得极小值时对应的对流比例。

表6 人员流率与对流比例的拟合方程Table 6 Fitting equation of flow rate and convection ratio of personnel
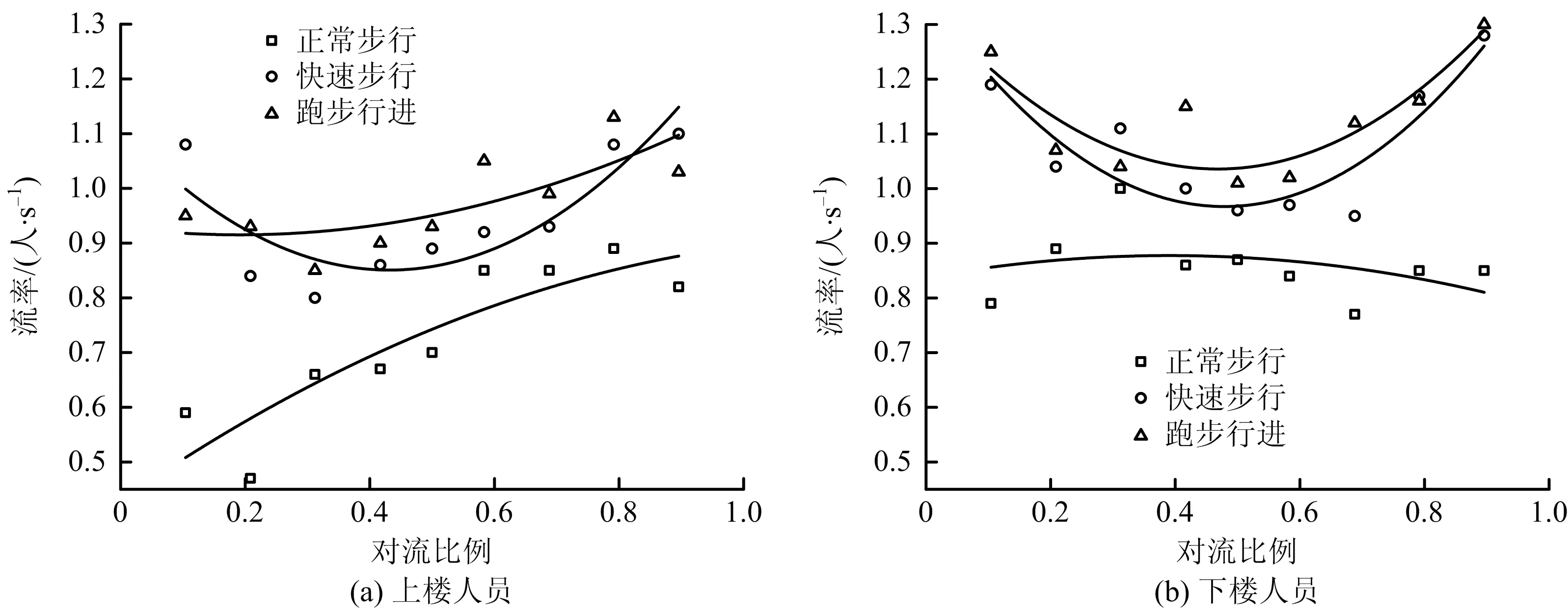
图9 人员流率-对流比例关系Fig.9 Relationship between flow rate and convection ratio of personnel
跑步上楼、正常步行上楼在实验涉及的对流比例范围内,流率几乎呈现随对流比例单调递增的趋势,说明从流率的角度考虑,上楼人员占比愈小,对于这2种工况而言愈不利。快速步行上楼、快速步行下楼及跑步下楼运动模式下流率随对流比例的增加先减小后增大,R0′值介于0.432~0.479之间,说明从人员流率的角度考虑,上楼人员略少于下楼人员时,对这3种运动模式下的流率而言是最不利工况。正常步行下楼的拟合方程的相关指数过小,说明对于该运动模式而言,流率与对流比例不存在显著的相关性。
4.4 速度与流率的关系
为揭示疏散速度与流率这2个关键参数之间的联系,此处将所有工况下速度-流率的对应数据,全部绘制在同一平面直角坐标系中,如图10所示。

图10 流率-速度关系Fig.10 Relationship between flow rate and speed
通过线性回归拟合得到速度-通行流率关系如式(7)~(8)所示:
上楼:
f=0.466v+0.527,r=0.691
(7)
下楼:
f=0.388v+0.628,r=0.628
(8)
采用线性相关显著性检验,取显著性系数α=0.05。上楼和下楼均包括3种运动模式、9种对流比例,共27种工况所对应的数据点,故n=27,此时临界相关系数r0=0.381。无论是上楼还是下楼,速度和流率的相关系数均明显大于此值,两者存在明显的线性正相关。因此,加快人员的运动速度,有利于提升楼梯的通行效率。在紧急疏散中应采取有效措施,保证人员可以采用快速步行或者跑步运动模式,以尽可能快的速度通过楼梯,进而提高单位时间内楼梯可通过的人数、缩短总体疏散时间。
5 结论
1)针对高层建筑楼梯人员单向下楼的情形:无论是否存在汇流,人员的运动速度会呈现出随楼层先加快-后减慢的变化趋势,流率则因为人员逐步分散而逐层递减;有汇流工况中,9~7层汇入楼梯的人员显著地影响9~5层的平均下楼速度,5层之后汇流对人员速度的影响逐渐减退;流率在首个汇流楼层(即本文实验中的9层)出现明显提升,后续楼层则因为人员分散的效应大于人员汇入的效应,流率仍呈现出逐层递减的趋势,但各层的流率均大于无汇流工况。
2)针对双层楼梯内人员双向对冲疏散的情形:当运动模式、对流比例相同时,上楼人员的速度、流率均小于下楼人员。对流比例对梯段上人员运动速度影响不显著;但对平台上人员运动速度以及人员流率存在显著的影响,二者的关系可以用二次函数表示,且在大部分工况中,存在1个对流比例使得速度或流率达到最不利状态。流率和人员的速度存在明显的线性正相关关系。

