矿工不安全行为的5M传播模型研究*

姜福川,安泽文

(1.辽宁工程技术大学 安全科学与工程学院,辽宁 葫芦岛 125105;2.辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室,辽宁 葫芦岛 125105)

0 引言

近年来,安全生产和健康工作逐渐成为工业发展中关注的焦点[1]。据《中国煤炭报》报道,2012年到2021年,全国煤矿百万吨死亡率由0.374降至0.044,下降88.23%[2]。国内煤矿百万吨死亡率呈现大幅下降的趋势,但煤矿死亡人数仍占我国高危行业死亡人数的半数以上[3]。已有研究表明,矿工的不安全行为直接影响煤矿安全事故的发生[4]。而矿工间的不安全行为传播是煤矿生产活动中重要事故隐患。为保障煤矿安全生产,探究如何抑制矿工不安全行为传播有重要意义。

目前,中外学者广泛关注职工的行为安全。Nasab等[5]分析职工的不安全行为演化问题;Li等[6]探究冲突管理策略对矿工不安全行为倾向生成机制有显著影响;Liu等[7]通过模型路径分析得出,矿工不安全行为的重要影响因素有2个,一是不安全领导力,二是不安全行为的先决条件;许正权等[8]研究发现,行为的成本收益、行为的可学习和模仿价值及社会接触是影响矿工不安全行为传播的关键条件;韩豫等[9]基于社会学习理论,提出控制不安全行为传播的策略。

就不安全行为传播而言,韩豫等[10]基于群体封闭性视角,发现不安全行为传播会受到一些内部因素的影响;陈晓宽等[11]为探究不安全行为的传播机制,建立矿工的群体压力、道德推脱、道德氛围与矿工不安全行为意向之间的假设模型;李红霞等[3]采用传播动力学方法,构建新SEIRS传播模型,研究转化率对稳态下进行不安全生产的矿工人数的影响。综上,虽然众多学者已对不安全行为影响因素、传播机理等进行一定研究,但关于不安全行为传播的动态研究仍相对有限;对于调节不安全行为传播系统稳态的转化率研究,目前主要关注单个转化率的改变对系统稳态的影响,未能从整体上考虑不安全行为稳定传播时系统的最优转化率。

鉴于此,本文在SEIR传播模型(其中S表示易感染状态,E表示潜伏状态,I表示感染传播状态,R表示免疫恢复状态)的基础上,结合传播动力学理论,建立矿工不安全行为的5M(M1-M2-M3-M4-M5)传播模型,同时以山西省3个不同煤矿综采工区的生产班为例,探究矿工不安全行为传播发生的机制;利用Python语言对模型展开仿真训练,找出重要的转化率和稳态传播时的最优转化率,以期预防煤矿生产安全事故的发生,降低事故率。

1 理论基础

1.1 传播动力学理论

传播动力学是通过研究互联网上计算机病毒的传播规律,在拓扑学基础上建立的科学理论[12]。在人类传染病的研究过程中,利用传播动力学建立的传播模型有SI模型、SIS模型等[13]。人类行为动力学通过构建动力学模型模拟预测人类行为,为分析不安全行为的传播提供新的研究范式[14]。人类行为传播机理与流行病的传播机理相似,此后又有学者提出SEIR模型[15]、SEIRS模型[10]等。传播动力学理论研究发现,即使有效传播率数值非常低,当模型中存在传播节点,不安全行为也可能传播到整个模型网络[16]。这表明构建1个与实际相对吻合的传播模型至关重要,并且模型中传播双方之间的传播率可能会影响系统最终的传播结果。

1.2 矿工不安全行为特点及传播机理

行为传播是1个过程,反映人类在人际交往基础上,发生的行为复制、扩散、演变等群体特征[17]。在煤矿企业生产活动中,矿工群体发生不安全行为的特点为传播、累积、重复性[8]。传播动力学理论认为,行为传播不是独立发生的,而是具有多重影响效应的[17-18]。

人类是群体活动的,煤矿班组生产过程中,不安全行为带来的效益会被班组成员进行模仿,出现传播效应。矿工间不安全行为的传播机理是:群体性的社会接触使个体性的不安全行为成为群体性行为,产生传播叠加或累积的效果,在这种效果达到一定程度后,形成对生产安全产生威胁的不良安全氛围,最终导致事故发生。实践中,群体内部的交际性社会网络是行为传播路径,且需要形成一定的条件基础。因此,事故的发生是不安全行为的传播在传播路径中被加强导致的。

2 矿工不安全行为传播模型的构建

2.1 模型可行性分析

矿工不安全行为传播特点和传播机理与传染性疾病传播机理类似,因此可构建传播动力学方程进行研究。根据传播动力学及行为传播理论,建立不安全行为传播模型,结合矿工群体特征,研究其不安全行为传播的规律和特点。

2.2 模型假设

假设1:结合实际情况,在特定的工作场所下,研究某个班组矿工的生产行为,不考虑输入与输出,保证班组矿工人数在选定时间段内维持恒定状态。按照矿工对不安全行为的了解程度,可以分为5类成员:不了解不安全行为的成员M1,了解不安全行为但尚未实践的成员M2,实践并传播不安全行为的成员M3,受上级制止而停止传播的成员M4,了解并拒绝传播的成员M5。M1(t)～M5(t)表示t时刻班组内部不同状态成员的人数比例(单位:%),是时间t的连续可导函数,因此M1(t)+M2(t)+M3(t)+M4(t)+M5(t)=1。

假设2:当不安全行为产生时,在特定的工作环境中,不同矿工的状态相互转化的概率称为转化率。这种转化率的影响因素包括个人安全素养m、组织安全氛围k、双方关系度n、组织管控力度l[19]。

假设3:单位时间内不同状态矿工接触的概率是相同的。

2.3 模型构建

5M传播模型的建立是在实际案例及专家意见基础上展开的,结合上述3个假设条件,矿工5M传播模型如图1所示。

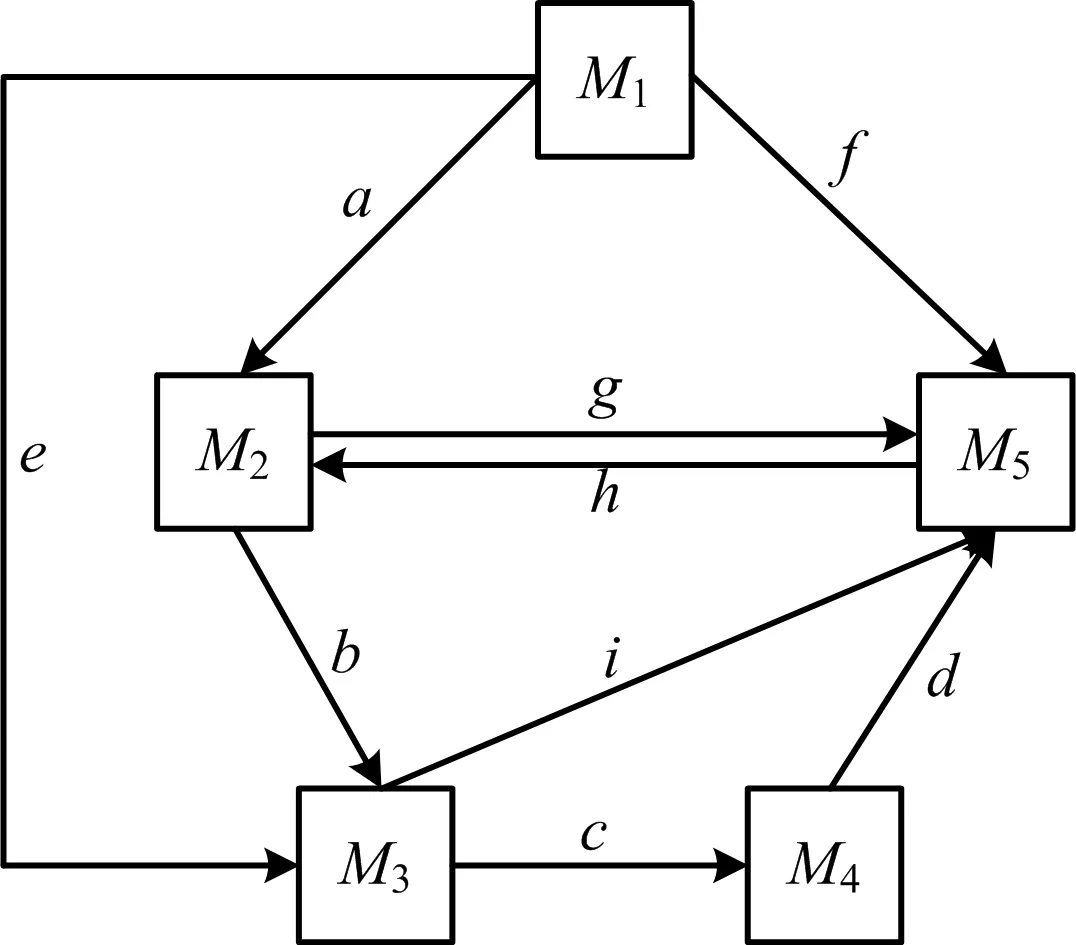
图1 矿工不安全行为5M传播模型Fig.1 5M propagation model for unsafe behavior of miners

图1中,a～i表示不同矿工状态进行转化的概率。M4的前提是实践并传播不安全行为,因此M4只能由M3转化而来。不同转化率的解释和假设具体如下。

1)由于工作需要,M1成员与M3成员接触,转化为M2成员的概率称为传播率。传播率a[20-22]如式(1)所示:

a=α1m1+β1n13+γ1k+δ1

(1)

式中:α1,β1,γ1,表示影响权重;m1表示M1中各成员的整体安全素养水平;n13表示M1成员与M3成员关系度的高低;k表示群体安全氛围水平;δ1表示随机干扰项。

2)恶化率b表示M2中各成员对不安全行为实践后未受到处罚,从而导致传播速率加快的概率,如式(2)所示:

b=α2m2+β2n23+γ2k+δ2

(2)

式中:α2,β2,γ2表示影响权重;m2表示M2中各成员的整体安全素养水平;n23表示M2成员与M3成员关系度的高低;δ2表示随机干扰项。

3)管控率c表示可能因不安全行为对企业安全造成一定的影响,组织领导对M3成员暂时管控,使其暂停传播的概率,如式(3)所示:

c=α3m3+γ3l+δ3

(3)

式中:α3,γ3表示影响权重;m3表示M3中各成员的整体安全素养水平;l代表群体对行为的管控力度;δ3表示随机干扰项。

4)整改率d表示经过组织整改,提升企业安全氛围水平,不安全行为不在M4成员间传播的概率,如式(4)所示:

d=α4m4+γ4k+δ4

(4)

式中:α4,γ4表示影响权重;m4表示M4中各成员的整体安全素养水平;δ4表示随机干扰项。

5)直接传播率e表示M1成员可能因缺乏安全知识直接转化为M3成员的概率,如式(5)所示:

e=α5m1+β5n13+γ5k+δ5

(5)

式中:α5,β5,γ5表示影响权重;δ5表示随机干扰项。

6)免疫率f表示M1中各成员因为风险厌恶或工作习惯等因素,直接转化为M5成员的概率,如式(6)所示:

f=α6m1+β6n15+γ6k+δ6

(6)

式中:α6,β6,γ6表示影响权重;n15表示M1成员与M5成员关系度的高低;δ6表示随机干扰项。

7)矫正率g表示M2成员可能因经过安全培训转化为M5成员的概率,如式(7)所示:

g=α7m2+β7n25+γ7k+δ7

(7)

式中:α7,β7,γ7表示影响权重;n25表示M2成员与M5成员关系度的高低;δ7表示随机干扰项。

8)遗忘率h表示M5成员可能由于记忆淡化或工作任务的加大,导致M2成员不断增加的概率,如式(8)所示:

h=α8m5+β8n25+γ8k+δ8

(8)

式中:α8,β8,γ8表示影响权重;m5代表M5中各成员的安全素养水平;δ8表示随机干扰项。

9)醒悟率i表示M3成员因害怕受到处罚,对不安全行为有所警惕,并拒绝传播的概率,如式(9)所示:

i=α9m3+β9n35+γ9k+δ9

(9)

式中:α9,β9,γ9表示影响权重;n35表示M3成员与M5成员关系度的高低;δ9表示随机干扰项。

依据理论模型建立微分动力学方程如式(10)所示:

(10)

本文拟进行矿工不安全行为5M传播模型的仿真试验,在实际案例的基础上,验证微分动力学方程的合理性。

3 实例分析

3.1 模型初始化

2022年8月,选择山西省3个不同煤矿综采工区的生产班组进行调研,了解班组中的人员组成情况等问题。模型参数的初始值采集方式为实地调查和网络访谈。通过调查访谈得知,3个不同煤矿的生产班组均是主要工作班组,具体人员组成情况如表1所示。

表1 各煤矿主要生产班组人员组成情况Table 1 Personnel composition of main production teams of each coal mine

生产班组1～3中,均包括采煤工、支护工等若干普工,以及班组长1名、副班长2～3名、安全员1～2名、验收员1名、监督领导1名等其他成员。班组中矿工不安全行为传播的情况主要通过问卷调查的方式收集数据,调查对象为生产班组中的全部人员。调查问卷采用线上填写的方式,持续时间为10 d,每天共发放94份,每天回收有效问卷至少88份,每天有效问卷回收率至少93.6%。问卷调查相关数据结果如表2所示。

表2 仿真值与调查值的对比Table 2 Comparison of simulated values and survey values 单位:%

式(10)代入参数后,出现无解情况,可利用Python进行数值仿真分析。在职工访谈、专家咨询、实地调查、查阅相关文献基础上[23],选择的起始时间节点为2022年7月1日(t=1),设定班组内处于不同状态的矿工人数比例初始值为M1(t)=90%,M2(t)=0%,M3(t)=10%,M4(t)=0%,M5(t)=0%;不同转换率初始值为a=0.2,b=0.2,c=0.3,d=0.3,e=0.2,f=0.1,g=0.1,h=0.1,i=0.1。取仿真时间t=30 d,5类矿工人数比例变化趋势如图2所示。

图2 各状态矿工30 d人数比例变化Fig.2 Change of proportion of miners in each state for 30 days

由表2可知,在矿工不安全行为传播的前7 d内,5种状态人数比例的平均误差分别为6.12%,2.96%,5.01%,7.45%,3.51%,表明仿真数据与调查数据相对吻合,模型能够客观反映不安全行为传播过程。由图2可知,当系统中各状态人数比例均趋于1个稳定值时,不安全行为传播达到稳态,系统稳态时间约为25 d。

3.2 各转化率对传播过程的影响

首先探究恶化率b对矿工不安全行为传播过程的影响,其他参数保持不变。恶化率b分别取0.2,0.4,0.6,0.8,探究各状态矿工人数比例随时间的变化规律,仿真结果如图3所示。

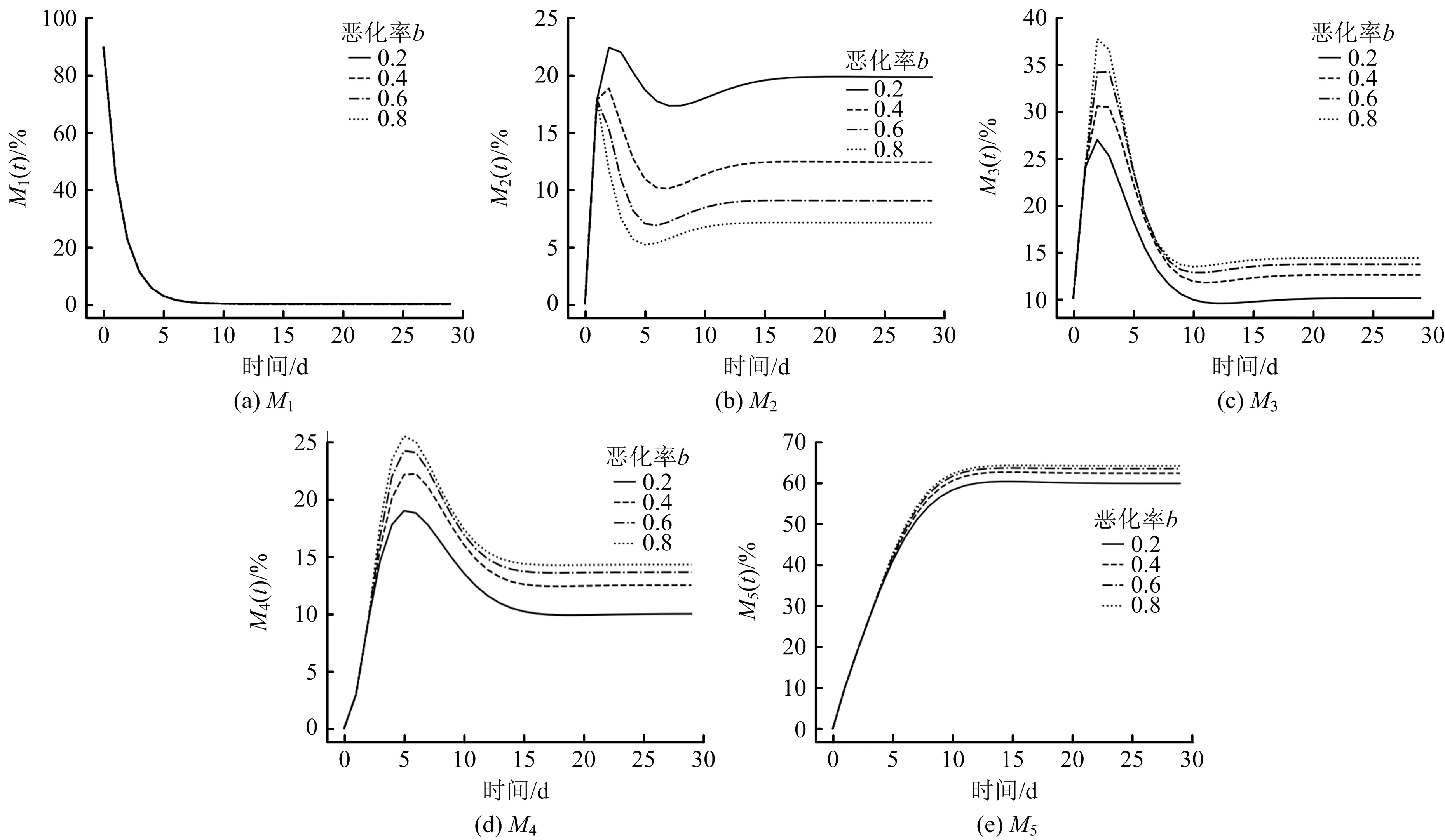
图3 不同状态下恶化率变化仿真曲线Fig.3 Simulation curves of deterioration rate change under different states

由图3可知,随着时间的增加,当恶化率b为0.2、0.4、0.6和0.8时,M1人数比例变化曲线完全相同;M2～M5人数比例变化曲线均有所变化。由此可见,不安全行为传播受恶化率影响较大。

按照上述恶化率变化仿真研究流程,分别探究传播率等8种不同转化率对系统稳态下各类矿工数量的影响,结果如表3所示。

表3 不同转化率对系统稳态的影响Table 3 Influence of different conversion rates on system steady-state

3.3 稳定传播时最优转化率分析

传播的彻底消失或趋于稳定,取决于1个存在的、确定的传播阈值,这是传播动力学理论的根本所在[24]。因此通过调节转化率,可使系统稳态时传播不安全行为的矿工数量最少,不安全行为传播速度最慢。由于转化率是取(0,1)之间的1个值,而根据本文实际情况,无法取得边界值。为了计算简便,将转化率a～i全部近似取(0.1,0.9)且步长为0.1的1个值。由各转化率的变化仿真结果,可得:1)传播率a的增大使M2峰值明显升高,存在M3增加的风险,因此a值取0.1;直接传播率e和免疫率f减小,不安全行为传播速度减慢,因此e,f取0.1;2)同一系统处于稳定状态的时间内,恶化率b、整改率d、遗忘率h的减少以及管控率c、矫正率g和醒悟率i的增加都会使M3稳态数量减少。

从M3的来源和去路分析,M3既可由M1、M2分别以e、b的概率转化而来,又可以c、i的概率转化为M4、M5。所以,e、b取最小值,c、i取最大值,才能使M3最小。这正与上述讨论的取值大小一致。因此,当转化率a～i值分别为0.1,0.1,0.9,0.1,0.1,0.1,0.9,0.1和0.9时,即可达到系统的最优转化率。

本文假设在班组内,不同状态矿工人数比例初始值维持恒定,仍为M1(t)=90%,M2(t)=0%,M3(t)=10%,M4(t)=0%,M5(t)=0%;系统的最优转化率为a=0.1,b=0.1,c=0.9,d=0.1,e=0.1,f=0.1,g=0.9,h=0.1,i=0.9。取仿真时间t=90 d,5类矿工人数比例变化趋势如图4所示。

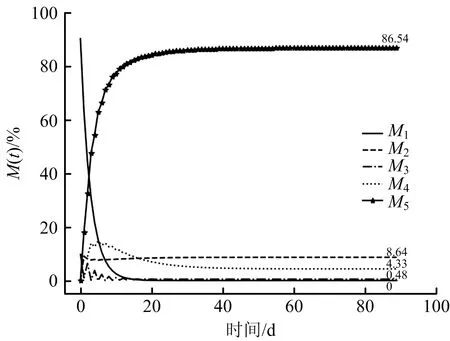
图4 各状态矿工90 d人数比例变化Fig.4 Change of proportion of miners in each state for 90 days

由图4可知,当取到系统的最优转化率时,系统稳定所用时间为80 d。此时,实践并传播不安全行为的成员M3所占比例达到最小值0.48%,不安全行为传播呈现稳定状态。比较图2和图4可得,调节转化率一方面可以控制不安全行为传播,减慢传播速度;另一方面可使传播不安全行为的矿工稳态数量占比达到最少,不安全行为传播得到抑制,使整个矿工系统的危害性降到最低。同时,也验证魏静等[24]学者的研究结论,系统的稳定性是由多个转化率共同作用的。

本文构建的5M模型是整体性分析,而且模型参数的确定方法是定性的,只采用访谈、咨询、实地考察等方法,对具体情况的分析尚不够全面。模拟仿真后对该班组进行跟踪调查,调查结果表明,仿真数据与该班组矿工不安全行为传播各阶段实际数据相差不大,从整体趋势上看是相对吻合的。

4 结论

1)5M传播模型能够客观反映矿工不安全行为的传播过程。矿工不安全行为的传播机制是群体性的社会接触使个体性的不安全行为成为群体性行为,产生传播叠加或累积的效果。因此,传播不安全行为的矿工对煤矿的安全生产有较大危害性,应对其重点关注。

2)转化率对不安全行为传播的影响较大,其中恶化率、整改率和遗忘率的提高会加剧不安全行为的传播,传播率、直接传播率和免疫率的提高,也会导致不安全行为传播速度加快,而提高管控率、矫正率和醒悟率可以抑制不安全行为的传播。

3)在保证系统达到稳态的前提下,通过求得并调节系统的最优转化率来抑制不安全行为的传播,可使整个矿工系统的危害性降到最低。