面向不平衡数据集的矿井通风系统智能故障诊断

赵 丹 ， 沈志远 ， 宋子豪

(1.辽宁工程技术大学 安全科学与工程学院, 辽宁 阜新 123000；2.辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室, 辽宁 葫芦岛125105)

如何及时准确的判断故障的位置，已成为煤矿亟待解决的一个难题[1-2]。随着煤矿智能化建设的发展，应用机器学习算法实现通风系统的智能故障诊断，助力矿井通风智能化管理是研究的关键[3]。

随着大数据、工业互联网、人工智能等技术的发展，故障诊断技术在电网[4]、机械设备[5]、航空航天[6]等不同工程领域应用成熟。2018 年，刘剑等[7-8]以风量作为输入特征，应用支持向量机(Support Vector Machine,SVM)算法确定了矿井通风系统故障位置及故障量，这开创了应用机器学习进行矿井通风系统故障诊断的先河，2020 年应用遗传算法构建了矿井通风系统故障诊断无监督模型，无需样本参与训练，有效提升了诊断性能；HUANG 等[9-11]利用卡尔曼滤波模型对矿井监测风速数据进行了预处理，并提出了基于混合编码算法的矿井通风系统无监督学习故障诊断模型，实现了故障位置和故障量的同时诊断；周启超等[12]基于改进的遗传算法对矿井通风系统故障诊断SVM 模型的参数进行了优化研究，有效避免了模型易出现过拟合的问题；倪景峰等[13-14]提出了基于随机森林和决策树的通风系统故障诊断方法，并证实了随机森林模型优于决策树模型；张浪等[15]选择了SVM、神经网络和随机森林(Random Forest,RF)3 种矿井通风系统故障诊断机器学习算法进行对比分析，结果表明神经网络模型具有更高的准确率；ZHAO 等[16]以大明矿为研究对象，在构建的故障巷道范围库内应用改进的SVM 算法进行通风系统故障诊断，缩减了故障定位的范围，提高了样本训练效率；WANG 等[17]构建了基于多标签K-近邻(Multi-label K-Nearest Neighbor,ML-KNN)的机器学习模型，解决了矿井通风系统多个位置发生故障时的快速诊断问题；LIU 等[18]应用4种机器学习算法：K-近邻(K-Nearest Neighbor,KNN)、多层感知机(Multilayer Perceptron,MLP)、SVM 和决策树(Decision Tree,DT)对矿井通风系统故障诊断模型性能进行了充分评价，确定了KNN 模型和DT 模型的优越性。虽然机器学习算法在矿井通风系统故障诊断中表现优异，但目前的矿井通风系统故障诊断模型的建立都是在数据集较为完备的前提下进行的。但是，在实际的通风系统故障情形下，完备的数据集条件是不能满足的。机器学习分类器高度依赖完备的样本集，不平衡的样本集训练出的模型通常不具有参考意义。如何在样本不平衡情况下开展故障诊断是一个严峻的挑战。机器学习领域的学者们通常从算法层面和数据层面解决不平衡数据的分类问题。文献[19]从算法层面出发构建了单分类支持向量机(One-Class SVM,OCISVM)与增量学习(Incremental Learnin-g,IL)相结合的通风系统故障诊断模型，但是该方法依赖于特定算法，导致适用性较差。

鉴于此，笔者从数据层面和网络体系层面开展不平衡数据集的通风系统故障诊断研究，构建了基于Wasserstein 距离的生成对抗网络(Wasserstein divergence for GANs,WGAN-div)，创新性地在WGAN-div模型中加入残差块实现原始数据增强处理，重构平衡数据集。结合集成学习中的投票机制实现通风网络分支故障诊断，确定了RF 模型在通风系统故障诊断中的优越性。有效解决了实际工况下样本不平衡的故障诊断问题，为智能诊断技术真正应用到矿井提供技术支撑。

1 处理不平衡数据集的改进模型

1.1 通风系统故障数据不平衡分析

矿井通风系统实际工况下，风门、风窗等含通风构筑物的巷道，采掘工作面，主要用风巷道，通风多分支交汇点处等位置更易发生故障，产生的故障数据较多，而其他分支故障概率较低，产生的故障数据较少，各个分支产生的故障数据样本数量存在很大的差距，存在数据不平衡问题。如图1 所示，不同颜色的五角星代表通风系统监测数据中的不同故障分支产生的故障样本，黄色五角星代表构筑物分支等易发生故障巷道产生的故障样本，为多数类故障样本集合；蓝色五角星代表其他不易发生故障的分支产生的故障样本，为少数类故障样本集合。

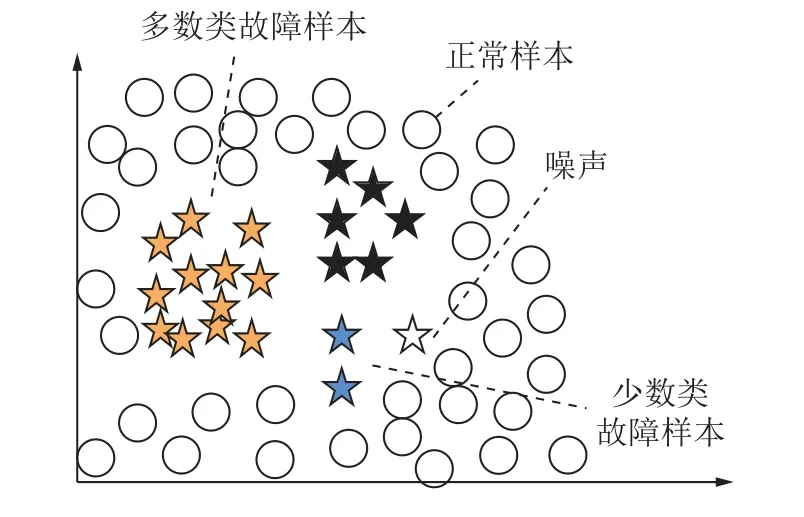
图1 数据不平衡示意Fig.1 Schematic diagram of data imbalance

矿井通风系统故障分支不平衡数据集可以描述为

式中，Xm为少数类故障分支数据集；Yn为多数类故障分支数据集；Sm+n为通风系统故障分支不平衡数据集；xi和yi为各数据集中的第i个样本数据；m为少数类样本个数；n为多数类样本个数。

1.2 传统的GAN 模型

生成对抗网络(Generative Adversarial Network,GAN)模型可以实现新样本数据的生成，从而达到调整Xm和Yn的类间平衡度的目的。GAN 模型主要由判别器D 和生成器G 两部分组成，其基本结构如图2 所示。生成器G 将随机噪声z映射到真实样本空间生成新的数据x˜；判别器D 判断x˜的真假即判别x˜为真实数据或生成数据。2 个网络交替训练，当判别器D 和生成器G 达到动态平衡时，新生成的数据与真实数据具有相似特征。

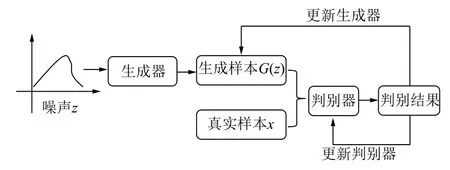
图2 GAN 模型基本结构Fig.2 Basic structure of GAN model

GAN 模型的损失函数为

其中，x为真实样本数据；Pz为随机噪声的分布；z为噪声；Mr为真实数据的分布；EG(z)～Pz为添加噪声的期望函数；Ex～Mr为真实数据的期望函数；G(·)为生成器的可微函数；D(·)为判别器的可微函数。实际上，生成器G 的损失函数相当于最小化生成数据分布和与真实数据分布之间的JS 散度，有

式中，PG为生成数据的分布；G*、D*分别为生成器损失函数和判别器损失函数的最优解；Ex～PG为生成数据的期望函数；JS 为JS 散度。

1.3 WGAN-div 模型

在GAN 训练初期，PG与Mr一般不会重叠，判别器D 容易判定数据的真假，但此时，该损失函数中的JS 散度退化为常数项lg 2，进而导致生成器G 的梯度消失，无法应用梯度下降法对网络进行训练，这使得传统GAN 模型出现训练不稳定的问题[20]。2017 年，ARJOVSKY 等[20]提出应用Wasserstein 距离代替JS(Jensen-Shannon)散度以解决传统GAN 模型梯度消失的问题，构建了基于Wasserstein 距离的生成对抗网络(Wasserstein GAN，WGAN)模型。但是在WGAN训练过程中，通常需要保持梯度的绝对值小于某个固定值，文献[21]提出了加入惩罚因子的GAN 模型(Wasserstein for GANs,WGAN-gp)模型，保证生成样本与真实样本之间满足Lipschitz 连续，但该方案并没有理论依据。对此，文献[22]提出了不需要Lipschitz约束的WGAN-div 模型，并在理论和应用上都证明了其优越性。基于前人的研究，笔者选择WGA-div 数据增强模型，损失函数为

式中，LG为生成器损失函数；LD为判别器损失函数；EG(z)～PG为生成器噪声的期望函数；Exˆ～pu为插值xˆ的期望函数，xˆ为生成样本与真实样本之间的随机插值，xˆ=αx+(1-α)G(z)，α为系数，α∈[0,1] ；pu为插值xˆ的分布；k、p为范数的幂，根据前人研究和实验测试，设置k=2、p=6。

1.4 残差块

文献[23]针对深度神经网络训练困难问题，提出了残差学习框架，能够简化深度神经网络的训练；文献[24]应用加入残差块的生成对抗网络实现了光伏数据的缺失值重构。鉴于此，为了防止使用深度卷积网络搭建的WGAN-div 模型在训练过程中出现梯度消失或网络退化的问题，笔者在判别器和生成器中加入了恒等映射残差块，残差块如图3 所示[23]。

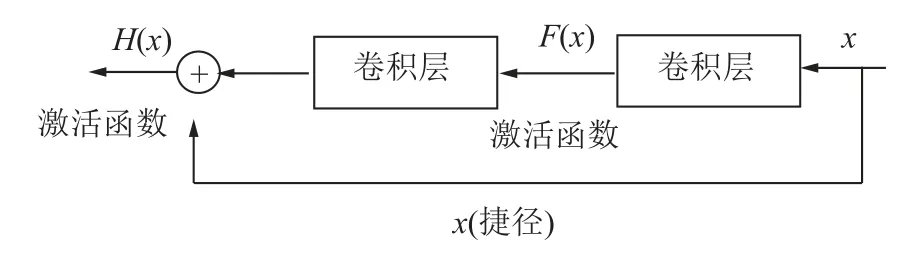
图3 残差块示意Fig.3 Schematic diagram of residual block

残差块以真实数据x为输入，主线径上有2 个卷积层，其目标函数为H(x)，定义为

其中，f(x,W)为映射函数；W为卷积层的权重。恒等映射残差块不仅可以学习x与H(x)的差别而且保证了2 者尺寸相同。残差块的引入使得网络的训练更容易，避免了梯度消失和梯度爆炸的问题。因此，笔者采用加入了残差块的WGAN-div 模型对通风系统监测数据不平衡样本进行数据扩充。将通风系统监测数据故障数据集中少数类样本个数由m调整到，进一步得到平衡数据集S′={Yn}，其中，为平衡后的少数类样本数据集。

2 基于WGAN-div-RF 的通风系统故障诊断

2.1 RF 分类模型

随机森林作为一种典型的集成学习模型，可以处理高维数据的分类，因此笔者选择RF 作为通风系统故障诊断多分类器。将风速数据作为RF 分类模型的输入，将故障分支编号作为RF 分类模型的输出。具体过程如下：对样本数据集进行Booststrap 采样，得到Kn个样本子集，应用子集训练出Kn个决策树，将测试数据输入Kn个决策树集合中得到N个结果，采用投票策略得到最终的分类结果为

式中，F(x)为Kn个决策树投票确定的矿井通风系统故障分支；fi为第i个决策树的分类模型；v为输入模型的特征参量，本文为风速数据； θi为用于训练第i个决策树的样本子集；I(·)为示性函数(分别以1 和0表示集合内是否存在该数值)；y为待判别的故障分支编号。

2.2 整体构架及流程

基于WGAN-div-RF 的通风系统故障诊断整体构架如图4 所示。具体流程如下：

(1)由于实际工况下矿井故障样本数据获取困难，本文应用智能矿井通风仿真系统(IMVS)模拟通风系统故障，构造通风系统故障不平衡数据集O，将数据集划分为测试样本集Ost和训练样本集Oin。

(2)应用WGAN-div 模型对不平衡的训练样本集Oin进行数据增强处理，生成新的故障样本On，将On加入到原训练样本集Oin中合成新的增广样本Oex。

(3)用平衡后的增广样本集Oex训练RF 模型，获得训练好的故障诊断模型。

(4)将测试样本集Ost输入训练好的RF 模型进行通风系统故障诊断。

2.3 评价指标

通风系统故障诊断多分类模型的评价通常建立在二分类混淆矩阵的基础上，对于样本不平衡的多分类问题，准确率指标难以实现对分类结果的准确评价，因此，文中增加了召回率Re、精确率Pr、Gmean、和F1分数对通风故障诊断模型进行综合评价。各个指标[25]的定义如下：

式中，A为模型故障诊断准确率；Pr和Re分别为模型的平均精确率和召回率；Gmean为召回率和特异度的几何平均值；N为输入模型的通风网络分支数，TPi为第i个故障分支的真正例；TNi为第i个故障分支的真负例；FPi为第i个故障分支的假正例；FNi为第i个故障分支的假负例。

3 不平衡数据对故障分支诊断影响实验分析

为了验证不平衡数据对通风系统故障诊断的影响，以图5 所示简单角联通风网络为例，设计不同不平衡比下的故障诊断实验。该网络中分支数为7，节点数为6，e1和e7分别为进风分支和回风分支，调节风窗安设在e4分支，风机特性方程为1 037.2+52.69q-0.52q2，其中，q为风量。通风参数见表1。采用智能矿井通风仿真系统IMVS 模拟分支故障[7](不包括源汇分支)，故障数据生成的具体方法参见文献[7]，按照不同的不平衡比生成4 组数据集，构造4组实验方案。

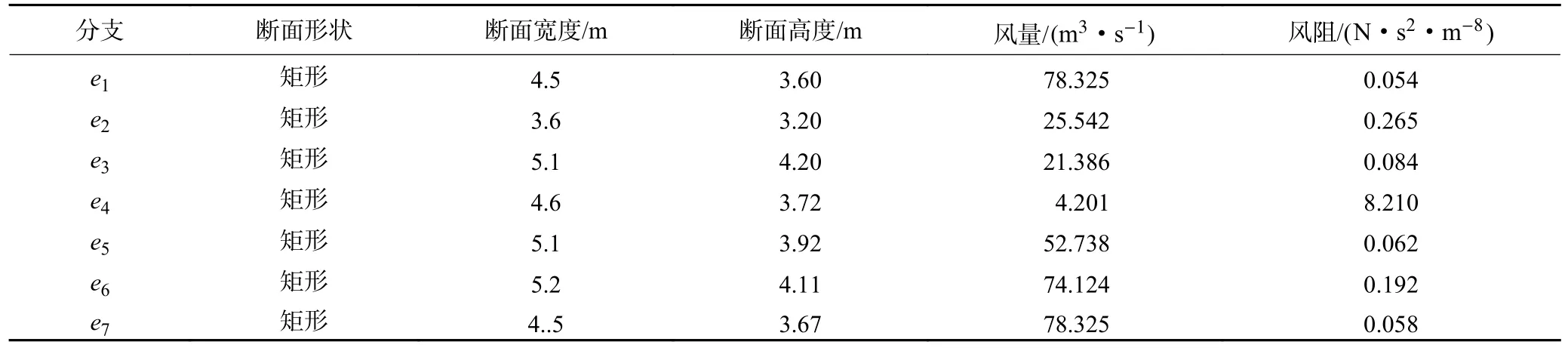
表1 简单网络各分支初始参数Table 1 Initial parameters of each branch of a simple network

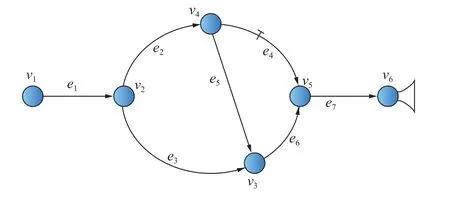
图5 简单通风网络Fig.5 Simple ventilation network diagram

e4分支安设了风窗，相较于其他分支更容易发生故障，因此通过增加e4分支的故障次数改变不平衡比。不平衡比分别设置为2∶1、5∶1、10∶1、20∶1，e4分支的模拟故障次数按照不平衡比的不同分别设置为100、250、500、1 000。为了方便比较，实验将少数类故障样本数量设置为相同，即除了e4分支外，e2、e3、e5、e6每个分支模拟故障50 次，相应的全部分支的故障样本总数分别为300、450、700、1 200，对应的实验方案分别记为T1、T2、T3、T4。每一组实验均对应一个平衡数据集作为对照实验组进行对比分析。为了保证实验对比的合理性，平衡数据集的故障样本总量应与不平衡数据集保持一致即每一组实验的故障样本总数应为300、450、700、1 200，由于平衡样本集中每一条分支的故障样本数应相同且排除源汇分支共有5 条分支，因此，平衡数据集中4 组实验各分支故障次数分别设置为60、90、140、240，对应的实验方案分别记为D1、D2、D3、D4。

为严格控制相关变量，在保证故障样本量一致的同时，各个实验模型均应在最优参数下运行才具备比较意义。以最大化F1 分数为目标进行调整，经十折交叉验证确定各实验RF 模型最佳参数，参数定义见表2，参数设置见表3。文中以风速特征作为输入，因此利用式(13)将通风网络解算得到的风量q转换为风速v。

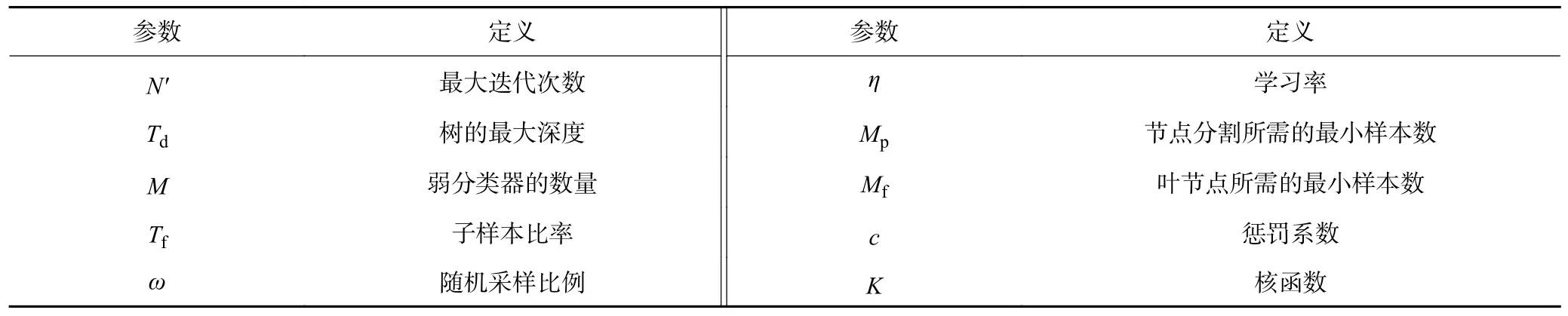
表2 分类模型参数定义Table 2 Definition of classification model parameters

表3 RF 模型参数Table 3 RF model parameters

其中，le巷道断面高度，m；we为巷道断面宽度，m。为以T1实验为例，其部分故障样本数据见表4，表中为各分支风速，m/s；为故障分支。将每一组实验数据集的70%划分为训练集，30%划分为测试集，以故障分支编号作为输出进行故障诊断实验，得到测试集的混淆矩阵如图6 所示，横坐标表示预测故障分支编号，纵坐标表示真实故障分支编号。实验T1～T4的综合评价指标结果如图7 所示。

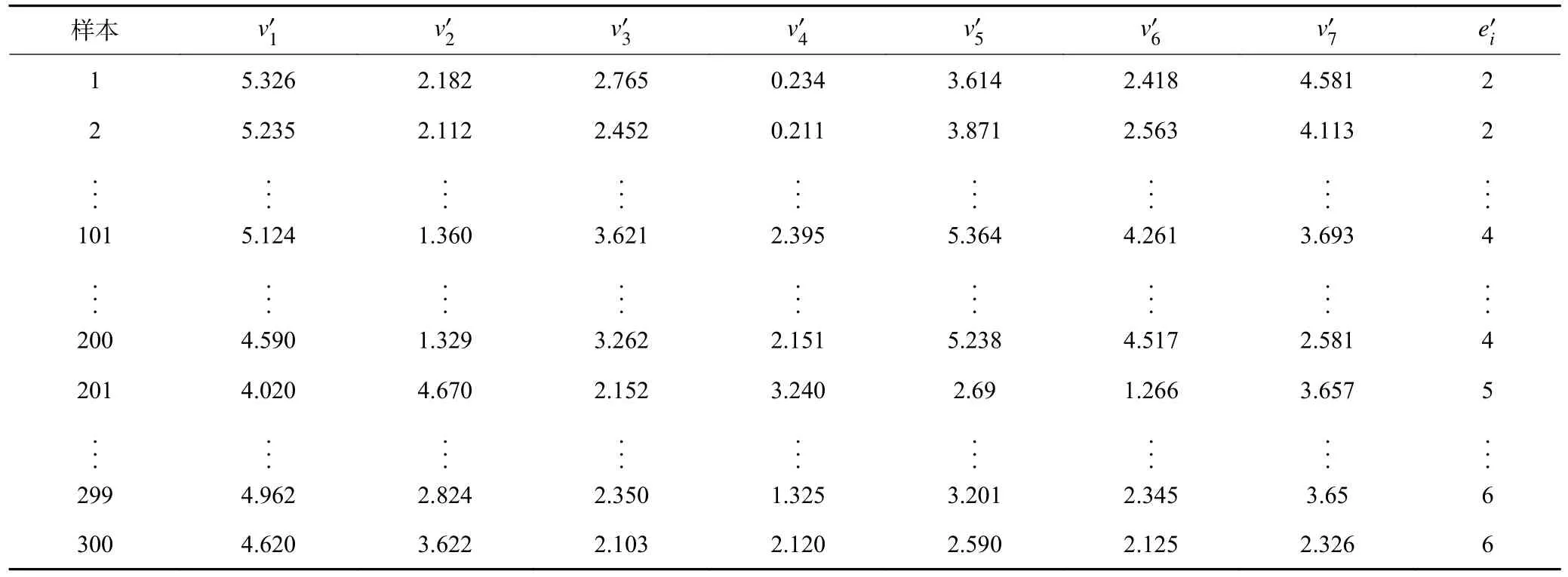
表4 T1 实验模拟故障样本集Table 4 T1 simulation fault sample set

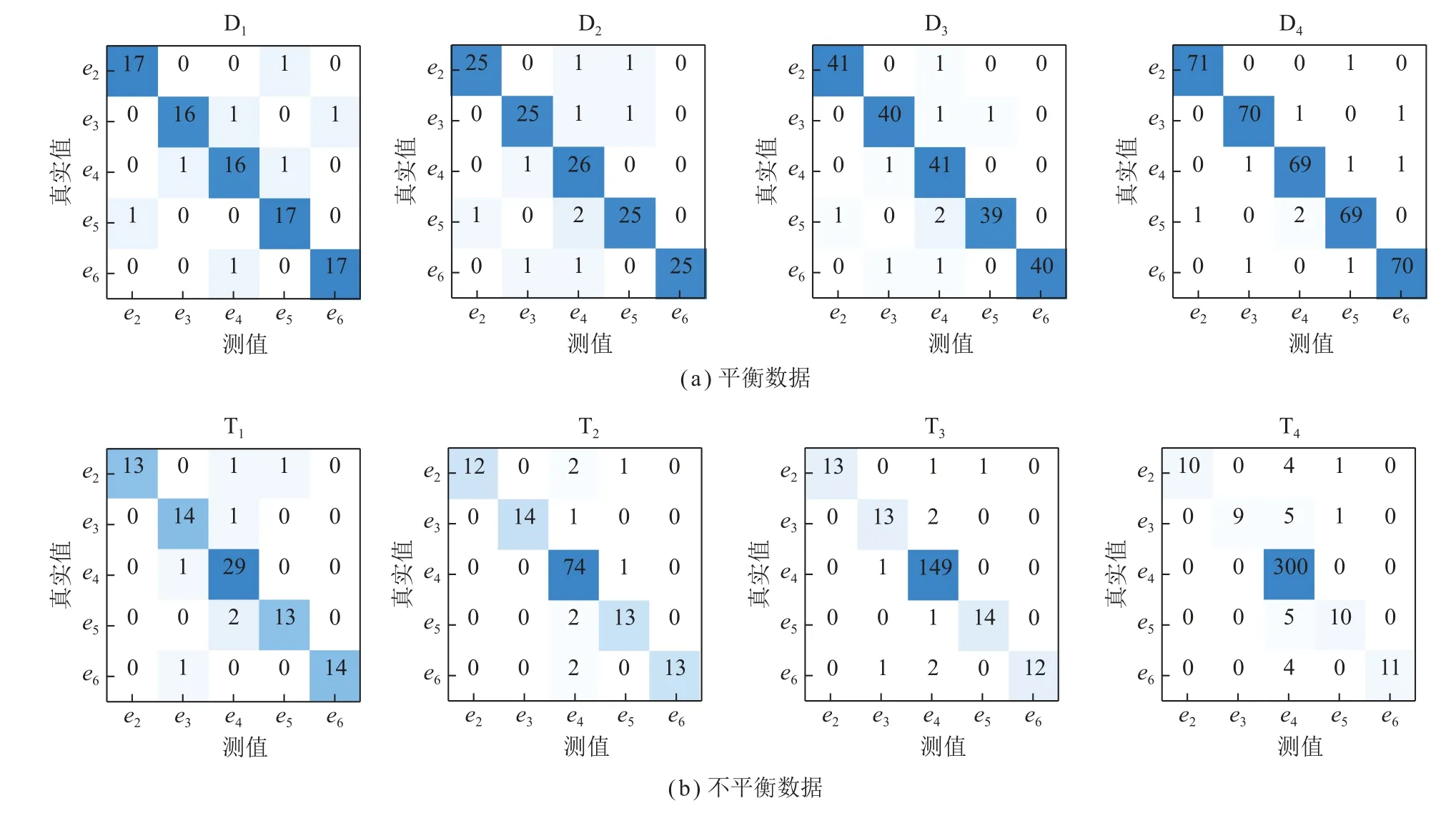
图6 简单通风网络故障诊断实验混淆矩阵Fig.6 Confusion matrix of simple ventilation network fault diagnosis experiment

图7 简单通风网络不平衡数据集故障诊断实验评价指标Fig.7 Experimental evaluation indexes of fault diagnosis in unbalanced data set of simple ventilation network

由图6(a)可知，实验D1～D4的平均准确率分别0.922、0.933、0.957、0.970，可以看出RF 分类模型能够有效地对通风系统故障进行诊断。但值得注意的是，理想的训练样本条件是获得良好诊断结果的前提，理想的训练样本不仅意味着故障样本数据充足，还以意味着故障样本数据中各个分支有着平衡的故障样本数量。然而，实际的矿井通风系统难以获得各分支故障样本均衡的数据集。由图6(b)和图7 可知，实验T1的Re、Pr、Gmean和F1分数平均值分别为0.91、0.93、0.90、0.92；实验T2的Re、Pr、Gmean和F1分数平均值分 别 为0.89、0.95、0.88、0.91；实 验T3的Re、Pr、Gmean和F1分数平均值分别为0.812、0.95、0.82、0.87；实验T4的Re、Pr、Gmean和F1分数平均值分别为0.73、0.95、0.81、0.78，可以看出随着不平衡比例的增加，除模型的精确率未发生明显变化之外，召回率、Gmean和F1分数不断降低，由此可见不平衡数据影响了模型的整体性能，其鲁棒性降低显著，不平衡数据使得模型出现漏判和误判的情况较多。尤其，由图7 中T4实验可知，当不平衡比为20∶1 时，各故障分支中Re的最大值为1，最小值为0.6；Pr的最大值为1，最小值为0.83；F1分数的最大值为0.96，最小值为0.73，各分支指标值的分布差异较大，分析认为数据不平衡易引起小析取问题，常规的机器学习分类器依据大量多数类分支(e4分支)数据规则建立模型，而忽略了其他少样本分支的数据特点，从而导致在分类时易将其他分支故障误诊断为多数类分支(e4分支)，随着不平衡比例的增加，故障样本被误判的比例逐渐升高，这进一步说明了不平衡数据集对通风系统故障诊断模型的危害，可见研究的必要性和实用性。

4 生产矿井实例实验分析

4.1 数据准备

笔者以鸡西矿业集团东山煤矿通风系统为例进行不平衡数据故障诊断实验。实验矿井的通风方式为对角式，该矿通风网络如图8 所示，分支数为96，节点数为84，总入风量14 394 m3/min，4 条进风井对应的分支编号分别为e2、e1、e23、e5，由南风井、西风井共同担负全矿井总回风任务，总排风量14 738 m3/min，对应的分支编号分别为e54、e92。安设风门的分支编号 为e47、e85、e28、e86、e48、e78、e22、e7、e30、e38、e29、e19、e65、e52、e84、e33；安设风窗的分支编号为e10、e83、e24、e13、e93。风机特性方程分别为：723.65+18.26q-0.17q2、614+45.2q-0.09q2。应用IMVS 模拟分支故障(不包括源汇分支)[7]，其中风门风窗构筑物所在分支模拟故障200 次，其他分支模拟故障10 次，得到5 120 组故障样本，数据不平衡比为20∶1。全矿共安设了15 台风速传感器，布设位置已在图8 中标出(本文以矿井实际安设的传感器为基础，不考虑传感器安设数量和配置的优化问题)。将风速传感器所在分支解算得到的风量数据经式(13)转换为风速数据作为模型的输入，部分数据见表5，表中为各分支风速，m/s；为故障分支。将标准化处理后的故障样本数据按照7∶3 的比例划分为训练样本和测试样本。

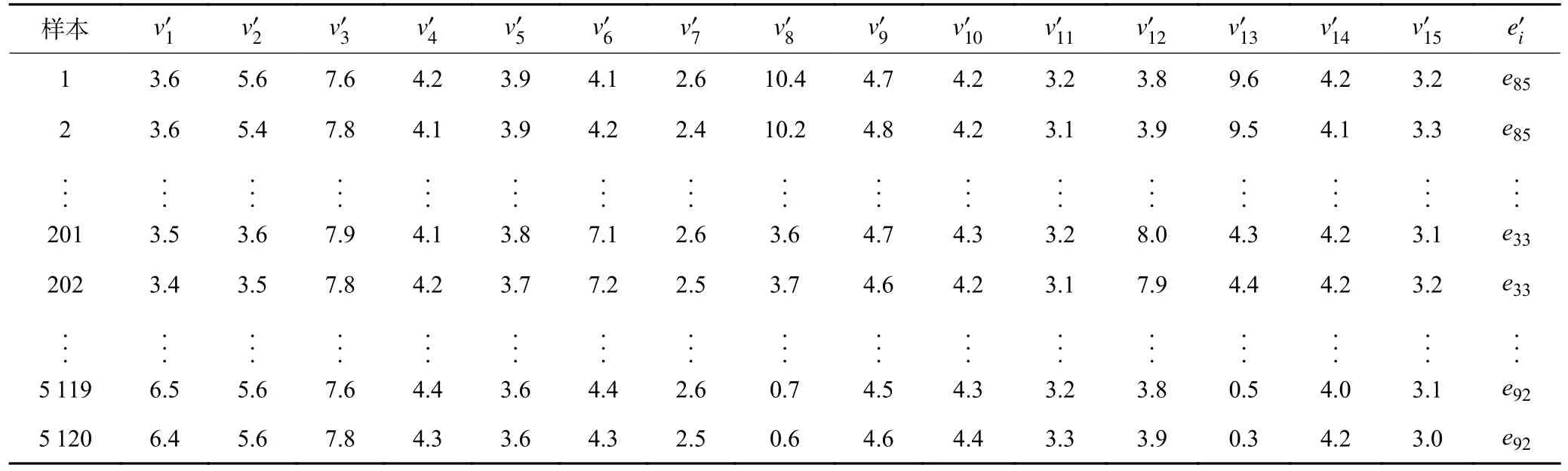
表5 生产矿井故障样本集Table 5 Fault sample set in production mine

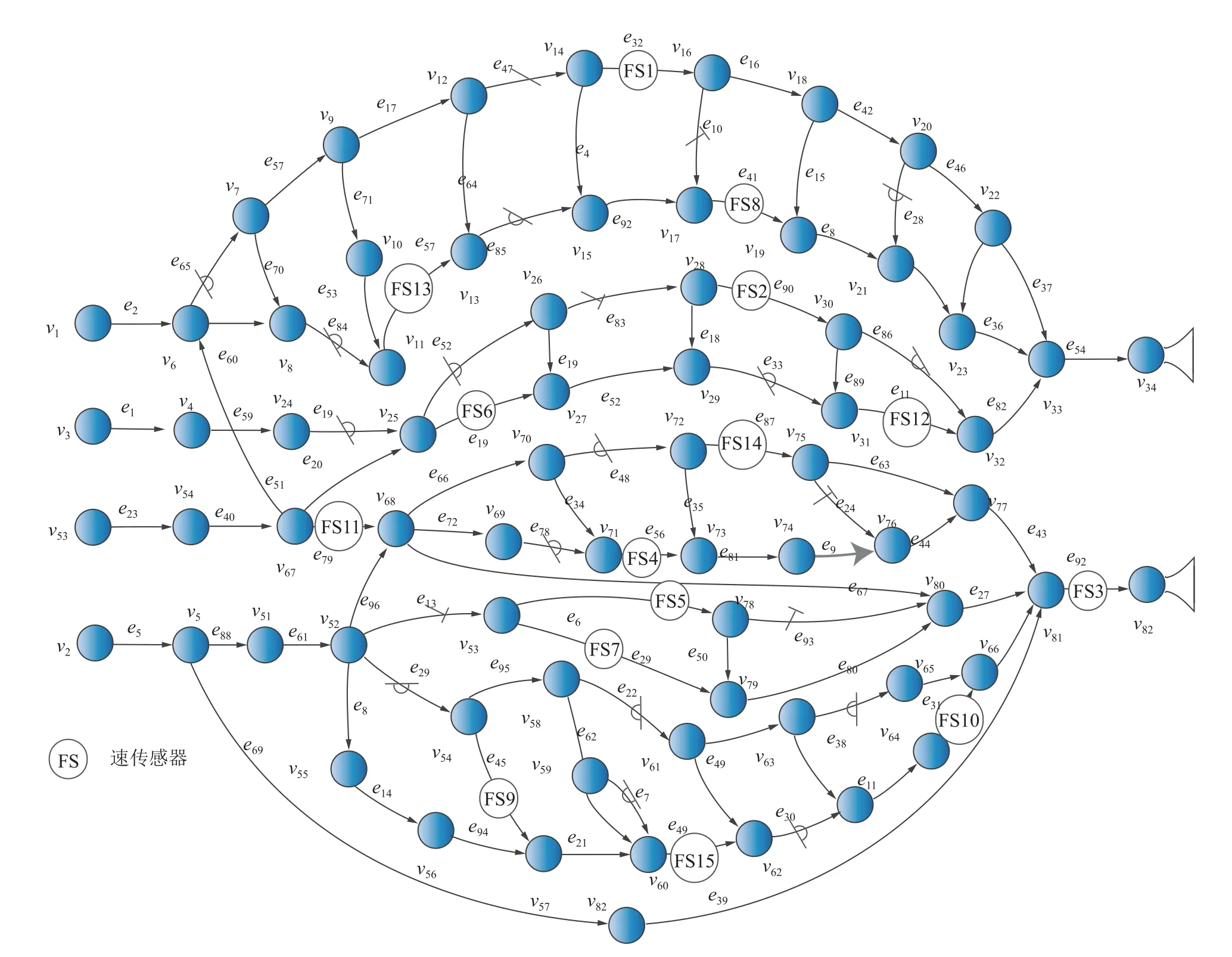
图8 东山矿通风网络Fig.8 Ventilation network of Dongshan coal mine

4.2 WGAN-div 有效性验证

为了验证WGAN-div 在通风系统不平衡数据处理的有效性，原始故障样本分别采用：① 原始数据集Din；② GAN 模型；③ WGAN 模型；④ WGAN-gp 模型；⑤ 本文所建WGAN-div 模型处理生成新的样本集On，使得合样本集Oex达到数据平衡，分类算法都选择RF 模型。本文构建的WGAN-div 模型生成器、判别器均包含3 个残差块，参数设置见表6。实验结果见表7，为10 次运行结果的平均值 ±标准差(最优结果加粗表示)。分析表6 可得出：

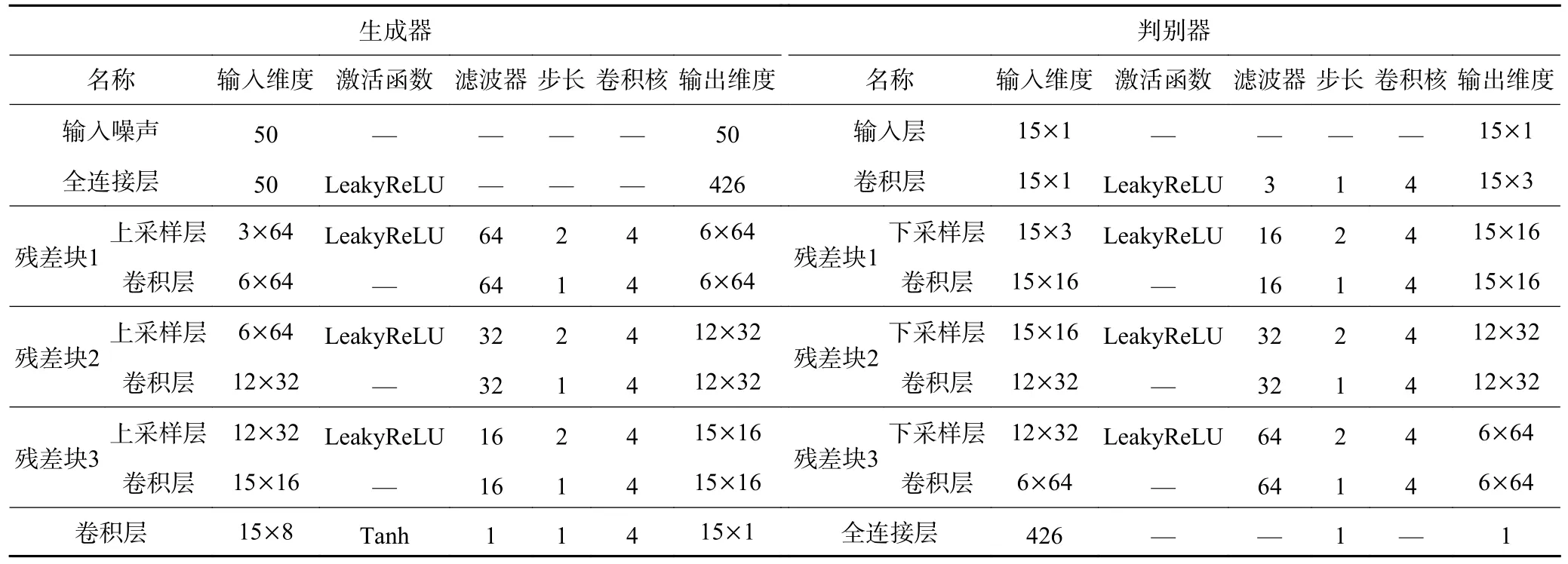
表6 WGAN-div 模型参数设置Table 6 WGAN-div model parameters

表7 不同数据增强方法的实验结果Table 7 Experimental results of different data enhancement methods

(1)直接采用RF 分类模型对原始不平衡数据集进行故障分支诊断，A、Pr、Gmean和F1分数都是最低。这意味着RF 模型不能准确识别出通风系统不平衡数据集中的少数类故障样本，因此，使用原始数据集不能实现对通风系统故障分支的有效诊断。

(2)对比原始数据集，基于WGAN-div 数据增强后，A提升了17.5%，Re提升了2.1%，Pr提升了24.2%，Gmean提升了17.1%，F1分数提升了14.4%。由此说明，利用WGAN-div 模型对不平衡的故障数据进行增强，能够有效提高原始数据的质量，进而提高分类器的判别性能。

(3)使用GAN、WGAN、WGAN-gp 进行数据增强后，虽然准确率和G-mean 指标均增大，分类模型对故障分支的识别能力增强，但是在F1分数上却没有任何明显的改进，分析认为模型扩充了劣质的新故障样本，影响了分类模型对故障分支诊断的判别。相较于GAN、WGAN、WGAN-gp 模型，WGAN-div 模型各项评价指标均为最高，A、Re、Pr、Gmean和F1分数分别为96.5%、96.2%、96.3%、96.1%和96.2%，大幅度提高了分类模型对故障分支的识别能力，验证了所提WGAN-div 模型在处理不平衡数据时的优越性。

应用t-分布随机领域嵌入(t-Stochastic Neighbor embedding,t-SNE)算法对WGAN-div 模型的样本生成情况进行降维可视化分析，图9 展示了迭代次数N分别0、100、200、500、800、1 000 时模型的生成样本与真实样本之间的分布情况，图10 展示模型损失函数的变化情况。观察图9、10，随着迭代次数的增加，WAGN-div 模型的损失函数稳定收敛、逐渐平稳，生成的新样本数据与真实数据分布逐渐交融，生成数据与真实数据具有很好的相似性，生成数据的质量越来越高。

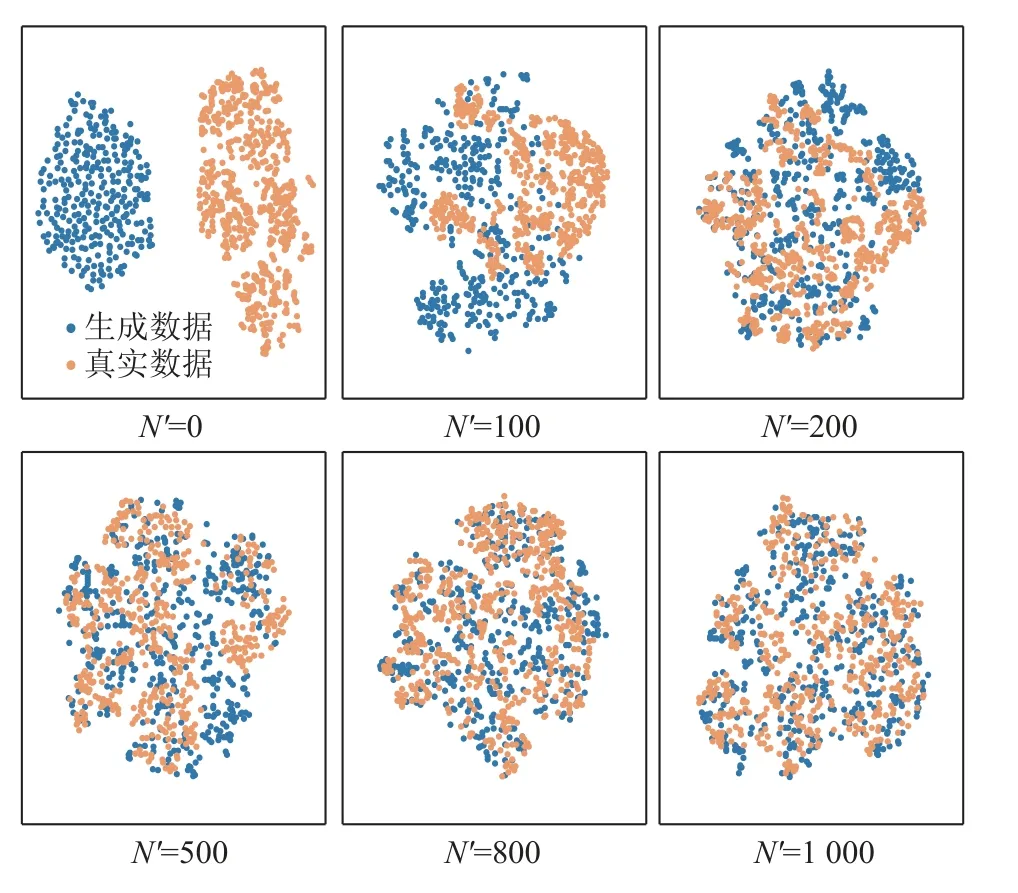
图9 t-SNE 降维数据可视化Fig.9 t-SNE dimension reduction data visualization

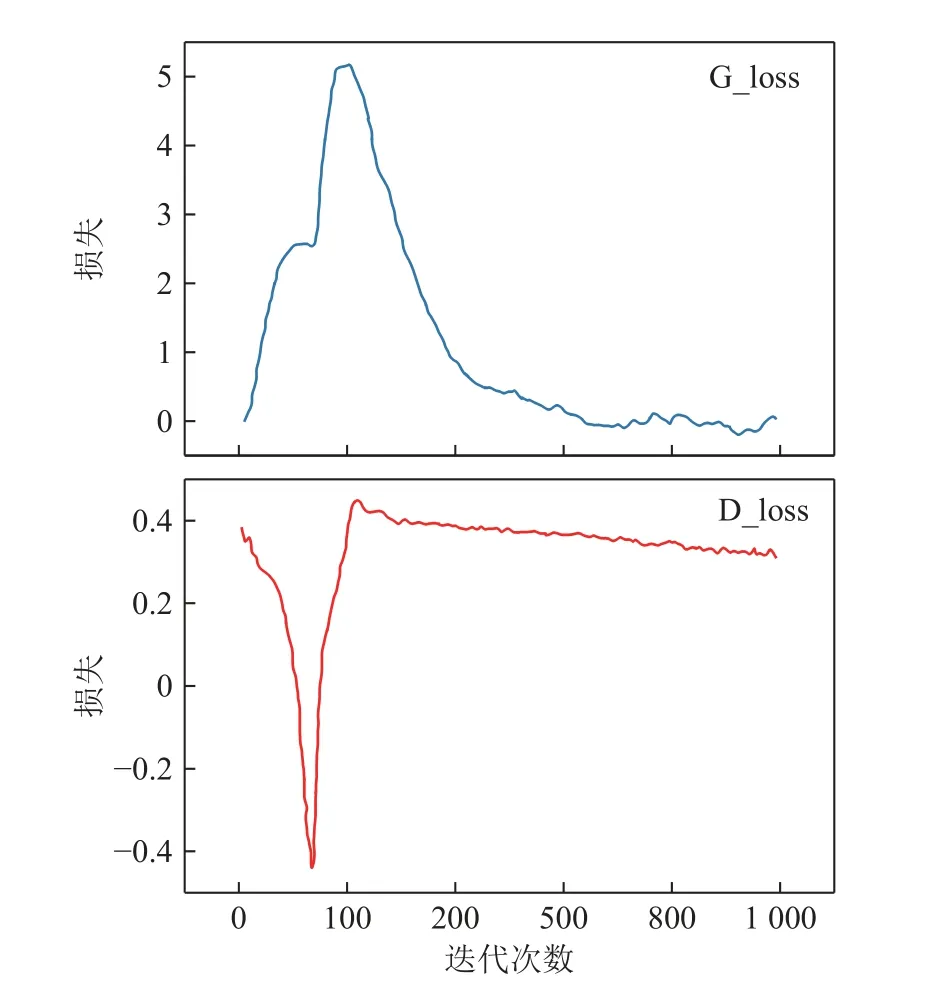
图10 WGAN-div 损失函数Fig.10 WGAN-div loss function

4.3 RF 有效性验证

为了验证RF 模型能够更有效的对通风系统故障分支进行辨别，原始样本经过WGAN-div 处理后，选用了以下经典的集成学习分类模型进行对比：类别提升树(CBT)、轻量梯度提升树(LGB)、梯度提升树(GBDT)，此外，将文献[7]中提出的通风系统故障诊断SVM 模型也纳入本文的对比实验。各个模型的最优参数见表8，各个参数定义见表2。

表8 分类模型最优参数Table 8 Optimal parameters of classification model

为了考察不同的数据生成比率下分类模型的表现是否具有明显改善，本文将WGAN-div 的数据生成比率分别调整为10%、20%、50%、80%、100%。图11展示了基于WGAN-div 不同数据生成比率下各分类模型的实验结果(10 次实验的平均值)，分析如下：

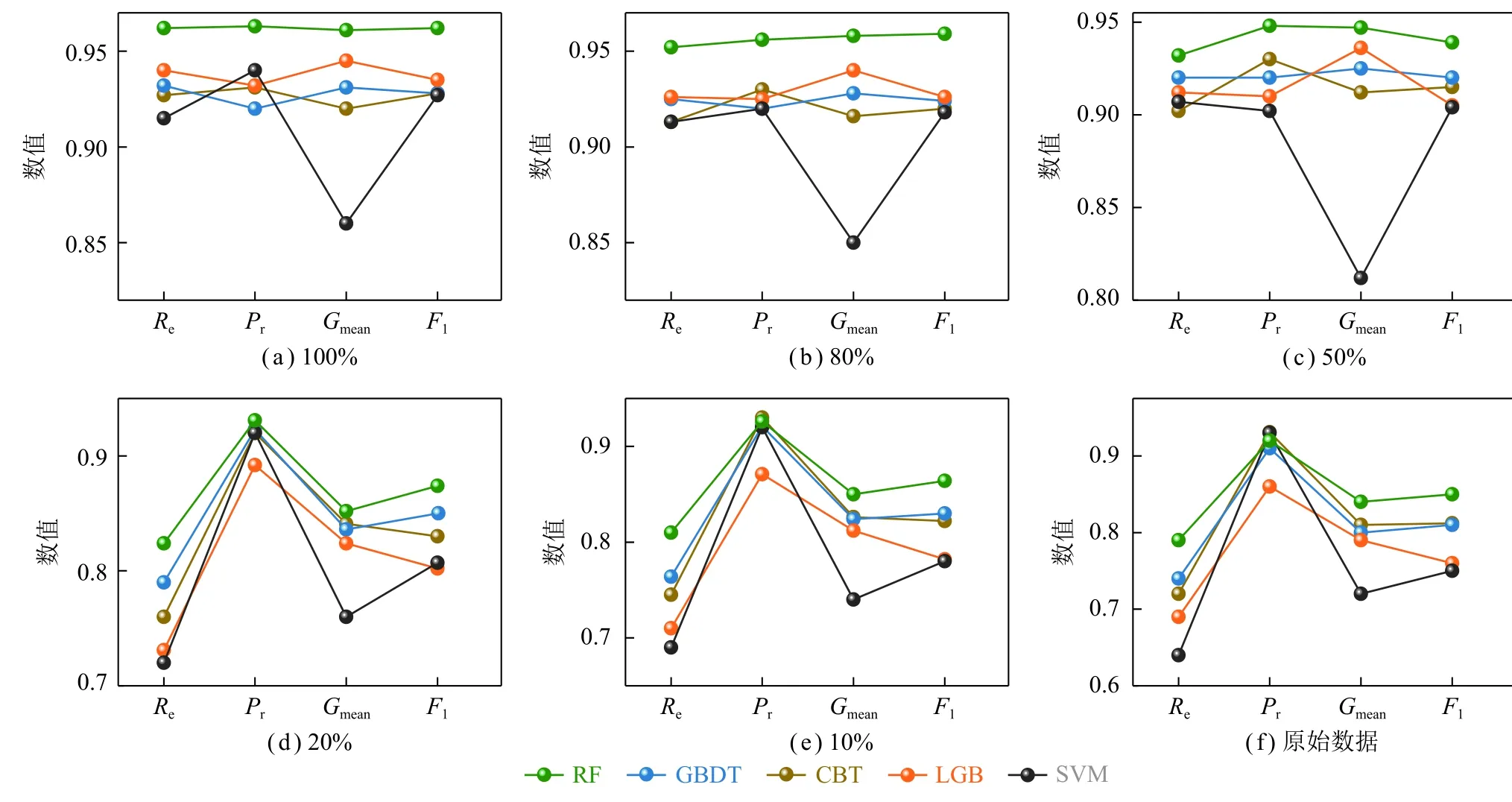
图11 不同数据生成比率下各分类模型的实验结果Fig.11 Experimental results of different classification models at different data generation rate

(1)从数据生成比率的角度来看，相较于原始数据集，数据生成比率为10%时，所有模型Re、Pr、Gmean和F1分数平均提高了2.7%、0.3%、1.8%和1.5%，模型性能提升不明显。但是，当数据生成比率达到50%时，所有模型的Re、Pr、Gmean和F1分数平均提高了19.8%、1.18%、13.4%和12%，所有分类模型的性能提升明显。新数据进一步生成达到80%时，模型表现的改进相对有限，即使数据生成比率达到100%时，各模型的性能达到最优，但是相对于50%的生成比率模型性能提升并不优越，因此当矿井通风系统故障分支较多时，考虑时间成本可以将数据生成比率设置为80%～100%。

(2)从分类模型的角度来看，RF 模型无论是在原不平衡数据集还是增广数据集上都表现出明显的优势。当样本数据达到完全平衡时，相较于原始数据集，RF 模型在Re、Pr、Gmean和F1评价指标上分别提升了21.9%、2.7%、11.8%、11.2%。在所有的分类模型中，传统的机器学习模型SVM 性能要明显弱于集成学习模型，尽管SVM 模型在F1 指标上的表现可以通过数据增强得到显著改善，但是其Gmean指标并未随着数据的平衡而明显改进，分析认为数据增强生成的伪样本具有一定的随机性，导致SVM 表现不够稳定。特别地，当扩充数据集达到平衡时，与传统的矿井通风系统SVM 故障诊断方法相比，RF 模型在Re、Pr、Gmean和F1指标上分别提高了4.7%、2.3%、10.1%、3.5%。总的来说，本文所提RF 模型适用于矿井通风系统故障诊断，当训练样本逐渐达到平衡时，RF 模型在A、Re、Pr、Gmean和F1得分上的表现较其他模型更具优势。

课题组在东山矿进行了2 次现场工业应用试验，考虑到生产安全和矿山的实际情况，通过打开关闭状态下的风门方式进行故障模拟，第1 次实验在确保东山矿安全生产的前提下打开了西采区6D 上左一回风巷的风门(图8 中的33 号分支)，风门开启后采集该矿15 个传感器的风速值(取风门开启后5 min 内各个传感器的平均值)，把15 个采集到的风速作为输入值，利用预测模型对故障分支进行预测，预测结果输出为33。第2 次实验打开了西采区3 号上右一巷的风门(图8 中的85 号分支)，将风门开启后采集到的15 个风速传感器值输入模型，预测结果输出为85，2 次试验故障分支预测结果与工业试验结果一致。

5 结 论

(1)从矿井通风系统实际工况下各分支故障概率不同的角度出发，以简单的T 型通风网络为例，说明了不平衡数据集对故障诊断模型的影响。建立了WGAN-div-RF 故障诊断模型，有效解决了通风系统故障数据不平衡的问题，从数据层面提高了分类模型的特征提取能力，进而提高分类模型的性能。

(2)故障诊断实验以及t-SNE 可视化结果表明，加入残差块的WGAN-div 模型能够生成高质量的新数据实现对样本集的扩充，WGAN-div 模型的A、Re、Pr、Gmean和F1分数分别为96.5%、96.2%、96.3%、96.1%和96.2%，相较于其他数据增强模型在处理不平衡数据时更具优越性。(3)针对通风系统故障诊断高维多分类问题，结合集成学习中的投票机制对通风网络分支进行分类，所得结果要优于传统的SVM 模型，其中RF 模型在不同数据生成比率上各评价指标得分较其他集成模型更具优势。