基于模糊自适应PI 控制和模型预测控制的MMC-HVDC 控制方法
侯世巍 杜昌顺 耿志强 韩永明*
(北京化工大学1.信息科学与技术学院;2.智能过程系统工程教育部工程研究中心, 北京 100029)
引 言
高压直流输电(high voltage direct current,HVDC)相较于交流输电有诸多优势,更适合应用于大容量远距离输电,而且其线路造价低、损耗小,可以实现不同频率的电网互联,为大容量输电的可靠性提供了保障[1-2]。 绝缘栅双极晶体管(insulated gate bipolar transistor, IGBT)是HVDC 系统的重要器件,由于单个IGBT 耐压水平有限,每个桥臂通常需要串联成百上千个IGBT,为了避免IGBT 电压分配不均必须采取严格的均压控制,同时又采用脉冲宽度调制策略,使得IGBT 开关频率高、开关损耗大。 模块化多电平换流器(modular multilevel converter,MMC)采用子模块串联的结构,解决了传统拓扑结构的均压控制难题[3],同时由于MMC 能够模块化,可以生成多电平波形实现任意电平数,具有波形质量高、失真度低等优点,MMC- HVDC 控制系统从而得到广泛应用[4-5]。 MMC-HVDC 控制系统作为柔性直流输电系统的核心,决定了系统的稳定性和运行性能,因此,对于MMC-HVDC 系统控制方法的研究很有必要。
MMC-HVDC 的系统级控制主要是对有功类和无功类变量的控制,其中有功类控制决定了系统的稳定运行,是系统安全运行的基础[6],无功类控制主要用于抑制电压波动。 Li 等[7]提出一种基于反馈线性化的非线性解耦控制方法,能够应用于有功和无功控制中,但这种解耦控制方法过程较为复杂和耗时,无法满足工程上的需求。 夏成军等[8]提出一种变目标MMC-HVDC 控制方法,通过将控制目标分解为多个目标,使系统快速无超调地分步达到指定目标,但是这种方法无法保证控制的可靠性。Liu 等[9]提出一种快速有限状态模型预测控制方法,提高了控制效率和控制系统的可靠性。 Zhang等[10]提出一种基于两相平稳坐标系的多目标模型预测控制方法,作为非对称故障发生时的MMCHVDC 系统控制方法,这种方法结合了经典的矢量控制方法并增加了权重系数,基于功能等效思想将控制系统分为电流指令预测、多目标控制和电压输出控制3 部分,避免了复杂的坐标变换,但此方法只适合于非对称故障情况下的MMC-HVDC 控制。
MMC-HVDC 系统稳定运行时,MMC 的3 个相单元产生的直流电压很难严格保持一致,从而导致相单元间有环流流动,增加系统损耗,因此需要进行环流抑制控制。 Zhang 等[11]提出一种基于改进的比例谐振(proportional resonance, PR)控制的MMC 环流抑制方法,通过改进比例谐振控制抑制谐波分量,得到电压补偿以补偿调制波信号,但该方法难以实现无静差跟踪。 Deng 等[12]通过分析由于桥臂阻抗不对称而产生的相间环流,提出一种使用MMC 的辅助电路实现环流抑制的控制方法,提升了MMCHVDC 系统的性能,但该方法的辅助电路结构较为复杂,控制性能较差。 杨晓峰等[13]提出虚拟阻抗滑模控制(virtual impedance sliding mode control, VISMC)环流抑制策略,建立了5 种模型的对比实验,并且通过稳态仿真数据的对比和分析验证了VISMC 环流抑制策略能显著降低环流二倍频分量,提高系统鲁棒性,但仍存在静差。
针对已有MMC-HVDC 系统控制方法存在的系统结构复杂、控制性能低的问题,本文提出了一种基于外环模糊自适应PI 控制和内环模型预测控制的MMC-HVDC 控制方法。 首先通过模糊自适应方法对外环PI 控制器参数进行实时整定,然后应用模糊预测控制方法改进传统内环控制,简化了系统结构,增强了动态响应性能。 针对系统存在的静差,使用准PR 环流抑制控制器来替换传统环流抑制控制器,消除静差值。
1 MMC-HVDC 控制系统结构
MMC 三相拓扑结构如图1 所示。 从图中可以看出MMC 由3 个器件结构完全相同的相单元组成,每个相单元由结构相同的上下两个桥臂构成,每个桥臂都包含N个完全相同的子模块SMi(i=1,2,…,N)。 子模块通过串联连接,同时每个桥臂串联一个阻抗L和一个等效损耗电阻R。 MMC 交流侧通过交流阻抗l和交流电阻r连接到三相交流电源。 MMC 桥臂串联的阻抗L和交流阻抗R构成了MMC 交直流系统功率传输的桥梁,其中uap、uan、ubp、ubn、ucp、ucn分别为三相上桥臂和下桥臂电压,iap、ian、ibp、ibn、icp、icn分别为三相上桥臂和下桥臂电流,p 代表上桥臂,n 代表下桥臂,ua、ub、uc分别为三相交流输出电压,ia、ib、ic分别为三相交流输出电流,Udc为MMC 直流侧额定电压。
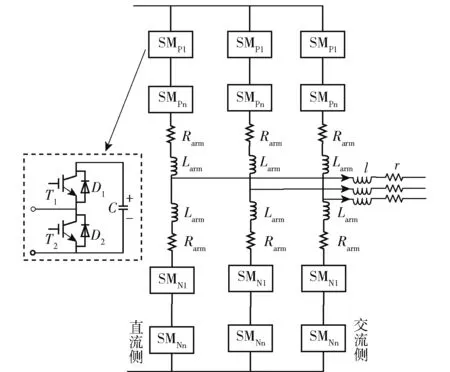
图1 MMC 三相拓扑结构Fig.1 MMC three-phase topology
基于MMC 的双端柔性直流输电系统称为MMC-HVDC,多端系统称为MMC-MTDC[14],这里以双端系统为例介绍MMC-HVDC 系统结构。 如图2 所示,两个交流系统的电力传输由两个背靠背的MMC 换流站和它们之间的直流线路完成。

图2 双端MMC-HVDC 系统结构Fig.2 Double-ended MMC-HVDC system structure
MMC-HVDC 的分层控制可分为系统级、换流站级和阀级3 个层次。 系统级控制为最高级控制;换流站级控制将系统级控制输出的有功和无功电流参考值转换为MMC 桥臂电压参考值,并将其通过调制波的方式输入到最底层阀级控制;换流器阀级控制通过合适的调制策略将获得的桥臂参考电压调制成MMC 子模块触发信号,通过控制IGBT 的导通与关断来实现对MMC 的控制。 除了上述控制外,MMC 还需要进行环流抑制控制[15]。
MMC-HVDC 的传统控制方法为直接电流控制,其优点在于控制环节简单,能够获得较高品质的电流响应。 该控制主要通过在同步旋转坐标系下搭配比例-积分(PI) 算法实现,分为外环与内环控制[16]。
2 MMC-HVDC 系统控制方法
本文应用的外环控制器为外环模糊自适应PI控制器,其使得系统能够实时整定参数,稳定性大大增加;内环控制器为内环模型预测控制器,减少了系统计算量,使得系统动态响应提高;环流抑制控制器为基于准PR 控制的环流抑制控制器,能够有效减少资源占用,同时实现更精准的跟踪效果。
2.1 MMC-HVDC 的外环与内环控制方法
以整流侧为例,基于外环模糊自适应PI 控制和内环模型预测控制(model predictive control, MPC)的MMC-HVDC 控制方法结构如图3 所示。
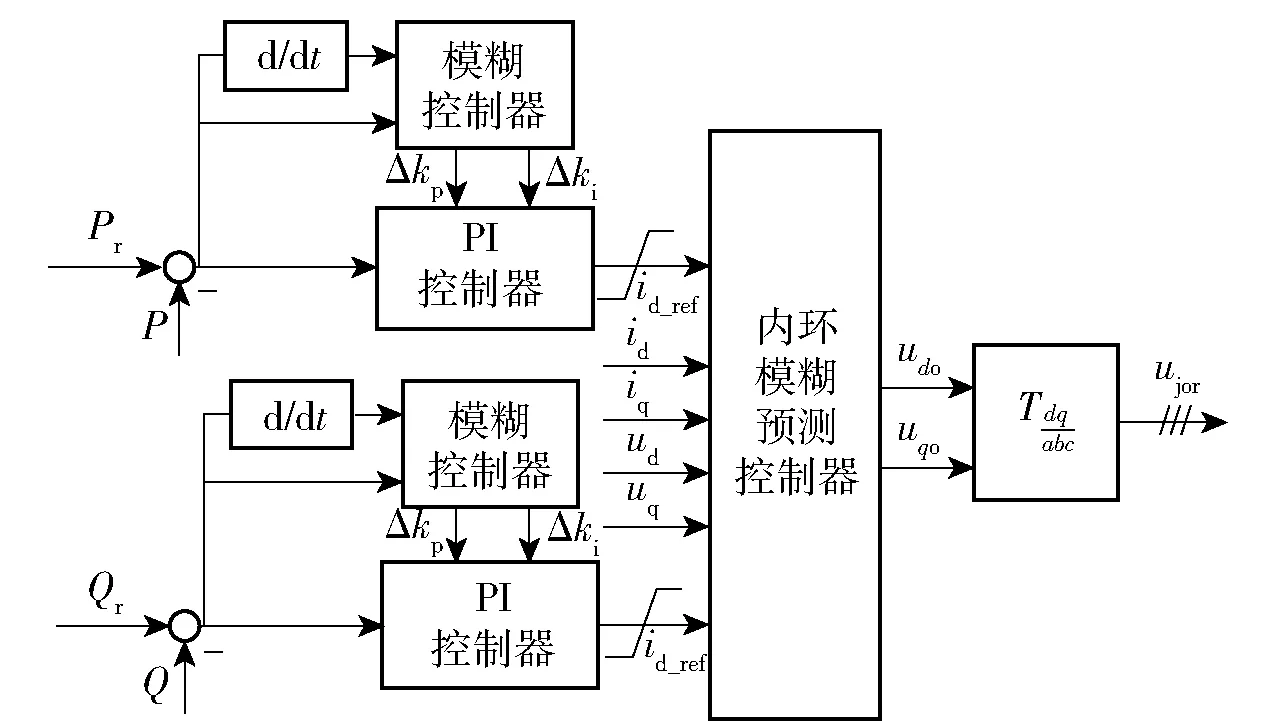
图3 MMC-HVDC 控制方法结构Fig.3 MMC-HVDC control method structure
从图3 可以看出,外环使用自适应模糊PI 控制器,输出的dq轴电流参考量作为内环MPC 控制器的输入进行电流控制,简化了dq旋转坐标系下的多个PI 控制环节,动态响应能力得到提高,优化了传统系统控制方法。
2.1.1 外环模糊自适应PI 控制方法
PI 控制是一种基于误差来消除误差的经典控制理论方法。 传统PI 控制存在局部稳定的局限性,当工况发生变化、被控对象模型参数发生变化,或者存在未知外部扰动时,PI 控制器的增益参数必须重新整定[17]。
模糊控制是解决控制系统中的不精确性的控制方法,因其能够控制滞后、多输入多输出系统且不受被控对象模型影响,鲁棒性好、结构简单,从而得到迅速发展。 模糊控制系统结构如图4 所示。

图4 模糊控制系统结构Fig.4 Fuzzy control system structure
模糊控制器按输入变量数量可划分为不同维数模糊控制器。 二维控制器相比一维控制器能更好地反映系统的动稳态性能,而多维控制器结构更为复杂且响应速度低[18],因此本文选用二维模糊控制器。 如图4 所示,使用误差e和误差变化率ec为输入,结合模糊化模块对输入变量e和ec进行模糊化处理。 数据库和规则库构成知识库,模糊推理根据知识库中的模糊逻辑关系和推理规则来处理经模糊化处理后的变量,得到控制模糊量。 最后,模糊量经清晰化模块转换为清晰量后得到实际控制量。 为了进一步减小抖震,提高响应速度和系统的自适应能力,选用自适应模糊增益调整的机械臂滑模控制策略。 因为采用模糊系统可以实现对任意连续函数的精确逼近[19],所以将外环PI 控制器替换为模糊自适应PI 控制器以改善传统外环控制性能,提高系统稳定性。
设计模糊自适应PI 控制器首先要确定其模糊规则:将输入误差e和误差变化率ec的模糊论域分别设置为[-9,9]和[-6,6],模糊子集都设计为{NB,NM,NS,ZE,PS,PM,PB},分别代表负大、负中、负小、零、正小、正中、正大,其中NB 和PB 隶属函数都使用Z 型,其他使用三角型[20]。e和ec的模糊子集分布如图5 所示。

图5 模糊子集分布Fig.5 Fuzzy subset distribution
比例控制在系统出现偏差后立即发挥控制作用,减少控制对象偏差值,但当比例系数过大时会增大系统超调导致系统动态性能变差。 积分控制能减小稳态误差,但由于其滞后性,作用太强会使系统不稳定。 所以,需要根据上述控制特性对误差及误差变化率来设置模糊自适应PI 控制参数调整规则,具体如下。
1)当e很大时,为避免偏差瞬间变大引起微分过饱和情况,kp应为较大值,但kp过大,也会引起控制器饱和输出;同时为了防止较大超调出现, 应取较小的ki值。
2)当e和ec大小适中时,为使超调量较小,应设置较小的kp值,同时ki值应适中,使得系统响应速度良好。
3)当e很小时,应将kp、ki设置为较大值来使系统的稳态性能保持良好,避免振荡以增强抗干扰性能。
根据上述分析,设置PI 参数的变化量Δkp控制调整规则如表1 所示。 表中PI 参数的变化量Δkp和Δki的模糊子集都设置为与ec相同的隶属函数。 此外,采用取中位数法作为清晰化方法[21]。
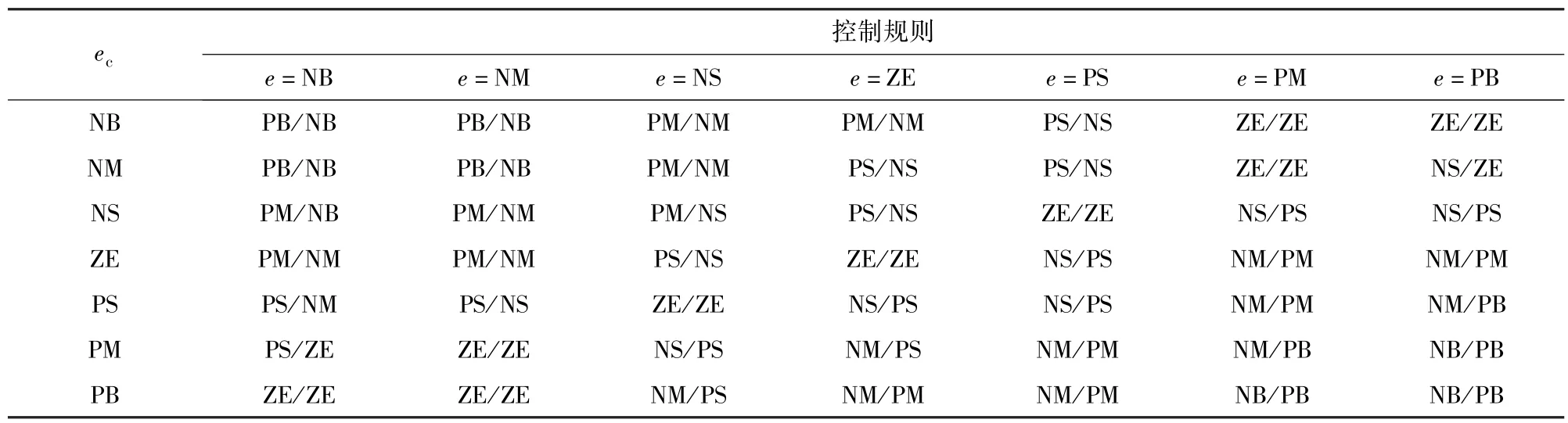
表1 Δkp/Δki 的控制调整规则Table 1 Adjustment rules for Δkp/Δki controls
外环模糊自适应PI 控制器结构如图6 所示,其中Pr、Qr、Ur均为输入信号,Pr代表定有功功率,Qr代表定无功功率,Ur代表定直流电压。

图6 外环模糊自适应PI 控制器结构Fig.6 Block diagram of the outer ring fuzzy adaptive PI controller
2.1.2 内环模型预测控制方法
模型预测控制以其灵活、鲁棒性强以及对非线性和多控制目标对象的适应性的优点成功应用于MMC 领域。 模型预测控制主要包括3 个环节,即预测模型、滚动优化和反馈校正,控制流程如下:将当前时刻的采样作为初值,利用系统的动态模型预测未来有限时域区间内的系统运动轨迹,同时优化求解在该时域区间内使得给定性能指标最优的控制量序列,将最优控制序列的首个控制值作用到系统控制中,在下一控制采样时刻,重复进行上述优化过程, 从而实现系统的滚动时域优化控制。 模型预测控制是一种基于模型的控制方法,其控制效果很大程度上依赖于模型的准确性,模型精度是影响MPC控制性能的重要因素[22]。 MPC 典型控制结构如图7 所示。
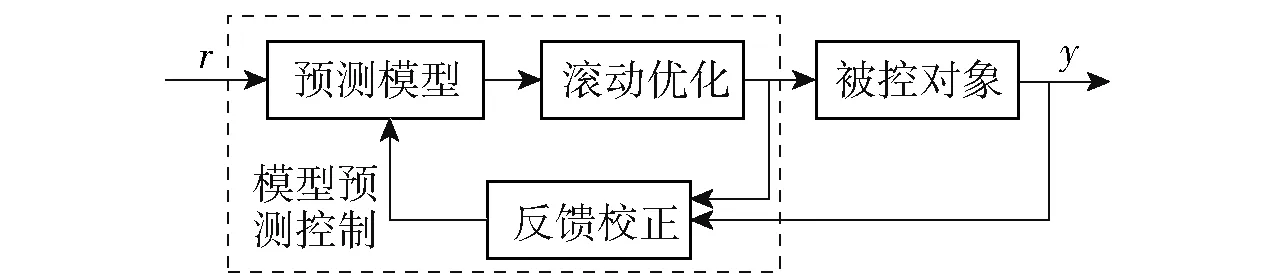
图7 MPC 典型控制结构Fig.7 Typical MPC control structure

图8 陷波滤波器伯德图Fig.8 Byrd diagram of the notch filter
一般控制系统状态方程为
式中,x(k)为k时刻系统状态量,u(k)为输入量。状态变量和输入量表达式为


式中,yp(k+1|k)表示k时刻对k+1 时刻的电流预测值。 系统控制目标是在k时刻使电流预测值接近参考电流值,所以控制目标函数可表示为
式中,S为输出量权矩阵,R为控制量权矩阵。
Yr(k+1)表示为
其中yr(k)为dq轴参考电流值。 为了使目标函数值最小,可对目标函数求偏导并令其等于零,有

2.2 基于准比例谐振控制的环流抑制控制方法
环流抑制控制方法在需要坐标变换的同时还要进行解耦过程,比较占用系统资源,同时由于此控制方法依靠静差值来进行控制,难以实现无静差跟踪[23]。 而基于准比例谐振(PR)环流抑制控制方法能够对相间环流进行抑制,减少资源占用的同时实现更精准的跟踪效果。
首先使用陷波滤波器提取桥臂电流中的二倍频分量。 陷波滤波器通过使环流在2ω处凹陷来进行提取,其传递函数为

使用PR 控制器来实现无静差跟踪,传递函数为
式中,kp为比例系数,kr为谐振系数,ω0为谐振频率。当kp=1,kr=10,ω0= 200π 时,其伯德图如图9所示。

图9 PR 控制器伯德图Fig.9 Byrd diagram of the PR controller
从图9 可以看出理想PR 控制器在谐振频率处有较大增益,但其他频率处的增益很小,当电网频率波动时此控制器不能有效抑制环流。
准PR 控制器能够在保障谐振频率处增益的同时增加控制器带宽,减少频率波动带来的影响,其传递函数如下。
式中,ωc为截止频率,且,H表示带宽。 以电网偏差要求±1 Hz 为例,此时H=2 Hz,则ωc=π,伯德图如图10 所示。
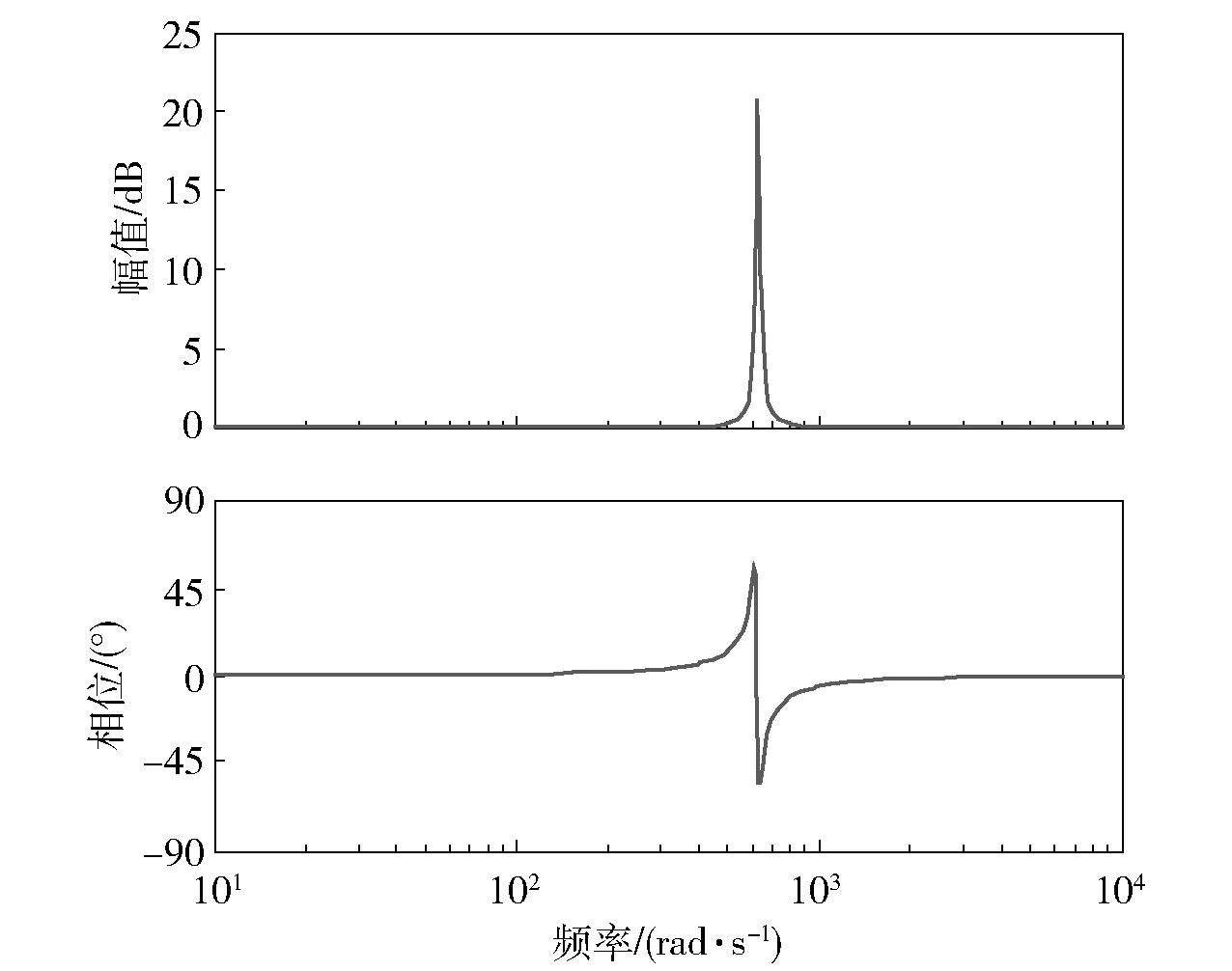
图10 准PR 控制器伯德图Fig.10 Byrd diagram of quasi-PR controller
根据上述分析,基于准PR 控制的环流抑制控制结构如图11 所示。
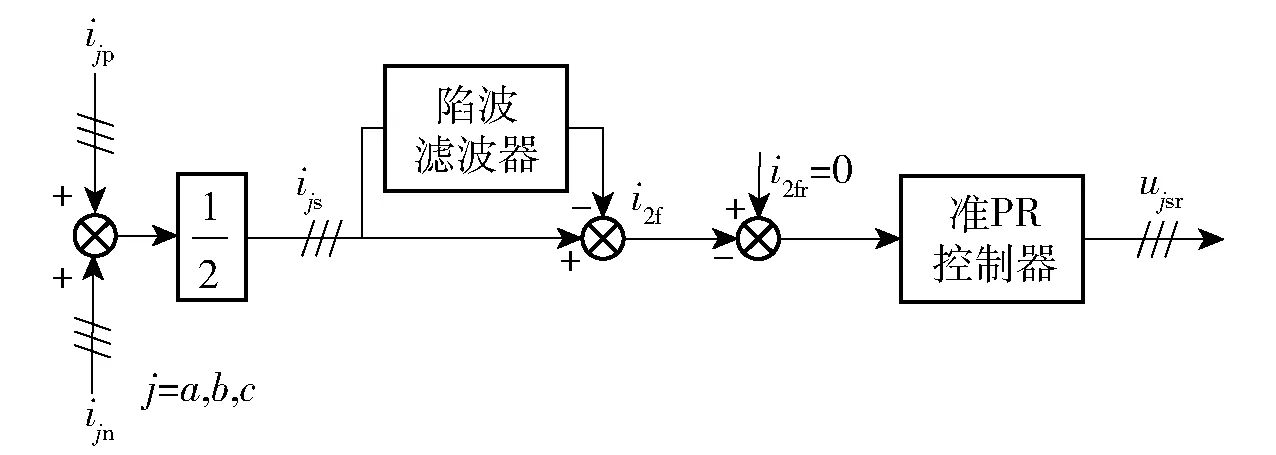
图11 基于准PR 控制的环流抑制控制方法结构Fig.11 Block diagram of the circulation suppression control method based on quasi-PR control
2.3 改进后的MMC-HVDC 系统控制方法
改进后的MMC-HVDC 控制系统主要包括外环模糊自适应PI 控制器、内环MPC 控制器和基于准PR 控制的环流抑制控制器,具体结构如图12 所示。
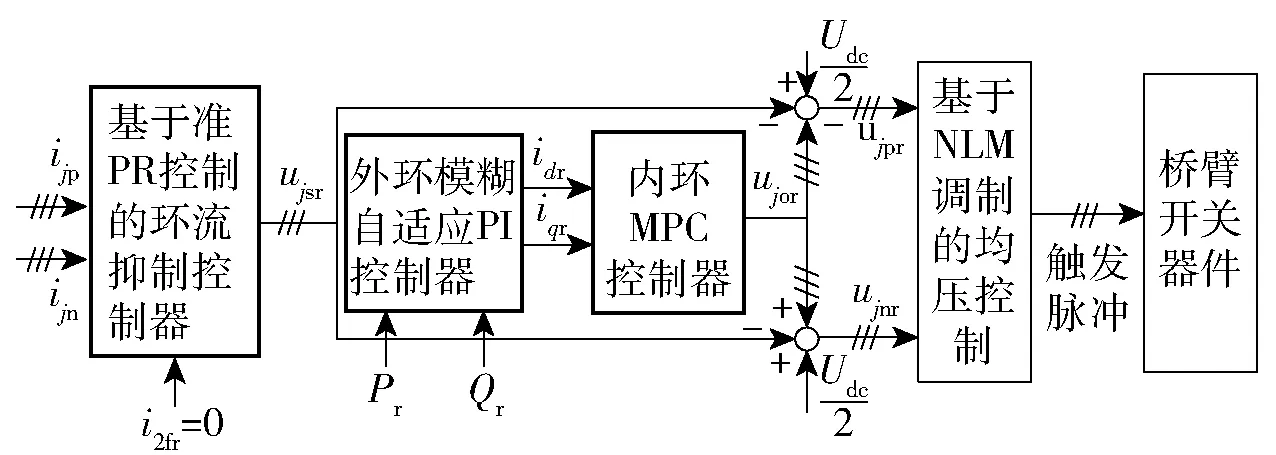
图12 改进后的MMC-HVDC 控制系统结构Fig.12 Block diagram of the control system of the improved MMC-HVDC
系统中的外环控制器选用模糊自适应PI 控制器,可以自适应实时整定控制参数,当系统参数变化时,其响应快、超调量小、控制性能好。 从图12 可以看出,输出的dq轴电流参考量作为内环MPC 控制器的输入进行电流控制,简化了dq旋转坐标系下的多个PI 控制环节,减少了系统计算量,同时动态响应能力得到提高,优化了传统系统控制方法。 内环控制器选用MPC 控制器,响应快、鲁棒性好,且适用于多变量控制,在工程中的应用较为广泛。 环流抑制控制器的作用为保障谐振频率处增益,并且能够增加控制器带宽以减少频率波动带来的影响。 由于每个子模块的电压的波动使得直流电压与上、下桥臂的电压之间存在电压误差,在保持上、下桥臂电压差值不变的前提下调整桥臂电压来补偿该电压误差,就能在不影响相电流输出精度的前提下,实现抑制环流的目的[24]。
3 仿真实验验证
在 Power Systems Computer Aided Design(PSCAD)软件中搭建改进后的MMC-HVDC 控制方法仿真系统,如图13 所示。
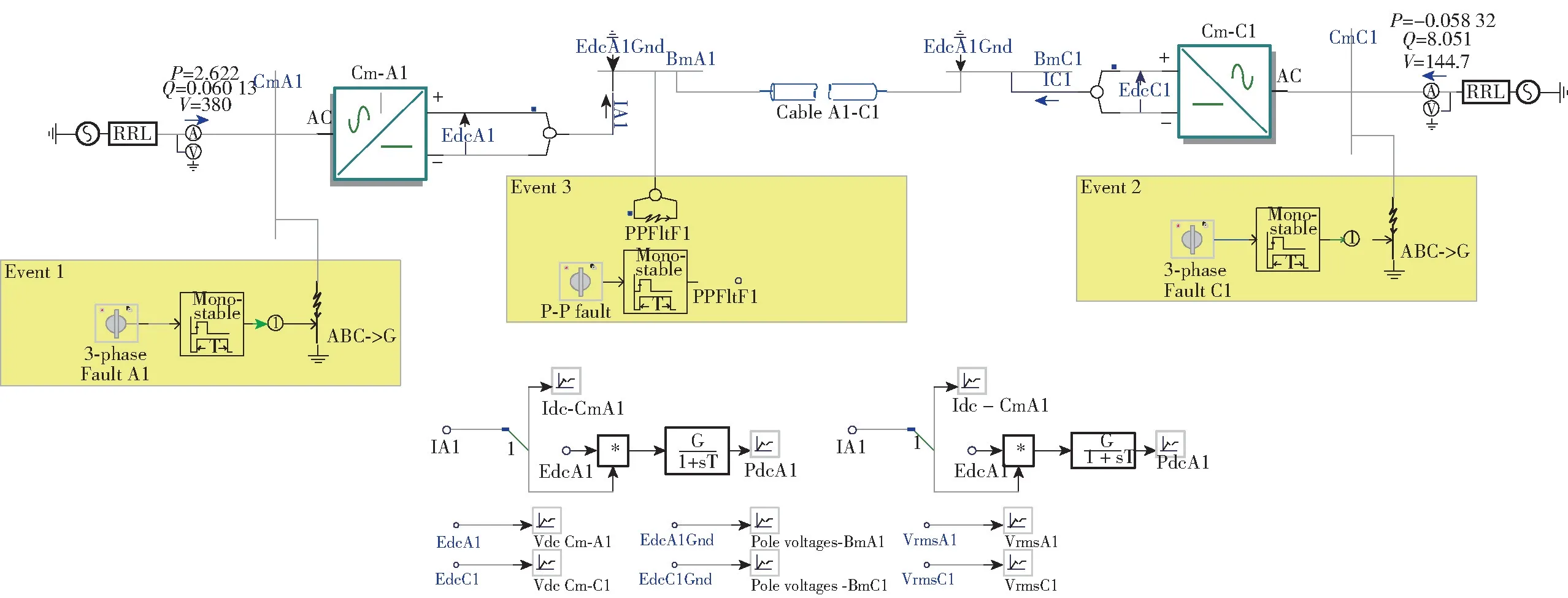
图13 改进后的MMC-HVDC 控制仿真系统Fig.13 Improved MMC-HVDC control simulation system
MMC-HVDC 系统主要包括MMC 换流器、外环控制器、内环控制器、环流抑制控制器、电容电压均衡控制模块等,为验证本文提出的基于外环模糊PI控制器的模型预测方法的有效性与优越性,在系统中进行了仿真验证,系统主要参数如表2 所示。

表2 MMC-HVDC 仿真系统主要参数Table 2 Main parameters for the MMC-HVDC simulation system
首先验证改进后系统的正常运行效果,改进控制方法后的系统参数曲线如图14 所示。 从图14(a)可以看出,交流侧相电压峰值约为400 kV,交流侧电压控制效果良好。 从图14(b)可以看出交流侧三相电流与参考值曲线重合,表明系统电流控制效果良好。 图14(c)为子模块电压之和随时间的变化曲线,电压峰值在预设的400 kV,表明系统稳定。 图14(d)为有功功率和无功功率变化曲线,可以看出系统在正常运行时能够稳定在预设值。

图14 改进控制方法后的系统参数曲线Fig.14 System parameter curves after improving the control method
为了验证本文提出的改进后的控制方法中基于准PR 控制的环流抑制控制方法的有效性,将其与基于PI 控制器的环流抑制控制器进行效果对比,结果如图15 所示。 在1.5 s 时开启环流抑制控制器,图15(a)为PI 环流抑制控制器开启前后的环流抑制情况,可以看出环流立即得到抑制,但仍然存在稳定量的相间环流,不能消除静差值。 图15(b)为PI环流抑制控制器开启前后的准PR 环流抑制控制器的环流情况,可看出环流立即被抑制甚至消除,环流的抑制作用明显,基本消除了静差值。 图16 为改进前后上下桥臂的电流情况。 在未使用环流抑制器时,由于环流的存在使得桥臂电流发生畸变,当环流得到抑制后桥臂电流波形得到明显改善,更接近正弦波,而在系统稳定后两种环流抑制控制方法的效果都较好。
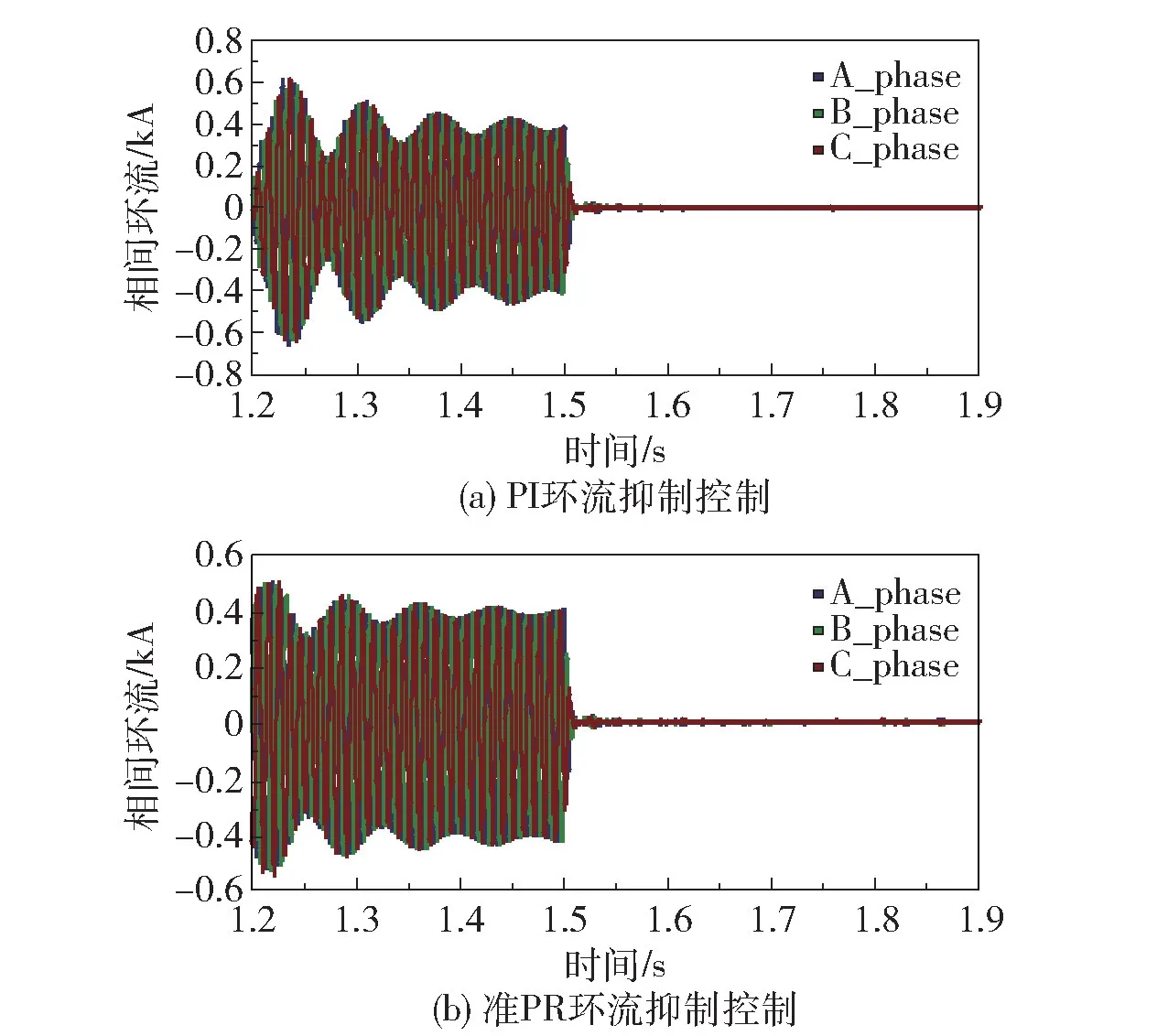
图15 相间环流Fig.15 Interphase circulation
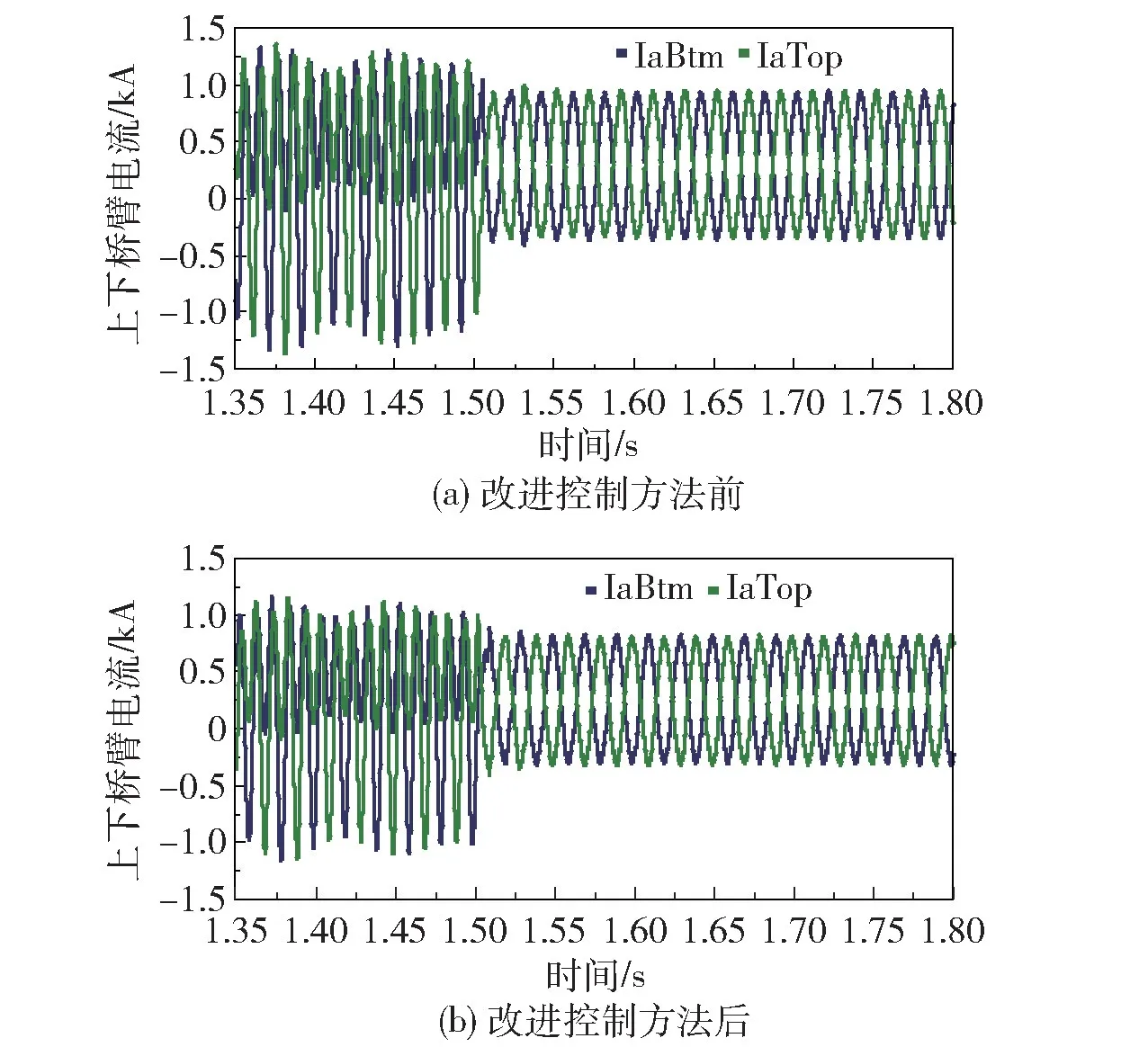
图16 上下桥臂电流Fig.16 Upper and lower bridge arm current
为验证改进控制方法后系统暂态响应的控制效果,在系统达到稳态后2 s 时,将系统有功功率从400 MW 突变到350 MW,三相交流电流暂态响应如图17 所示。

图17 三相交流电流暂态响应Fig.17 Three-phase AC current transient response
三相交流电流在0.5 s 时就重新稳定,有功功率降低,电流值也相应降低,电流控制效果良好。 在系统达到稳态后3 s 时,将直流侧电压参考值从400 kV 突变为500 kV,改进前后电压的暂态响应情况如图18 所示。 改进后的调节时间约为0.05 s,而改进前的调节时间为0.15 s,表明系统的暂态效果得到明显提升。 图19 为改进前后A 相桥臂子模块的电压情况。 在新的直流侧电压参考值下,子模块电压的新的标准值应为2.5 kV,0.1 s 左右子模块电压达到新的稳态且在参考值上下波动,波动范围在4%以内,表明子模块电压的暂态响应控制效果良好。
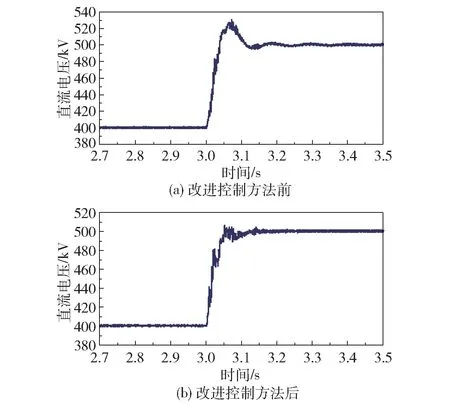
图18 改进控制方法前后的直流电压Fig.18 DC voltage before and after improving the control method
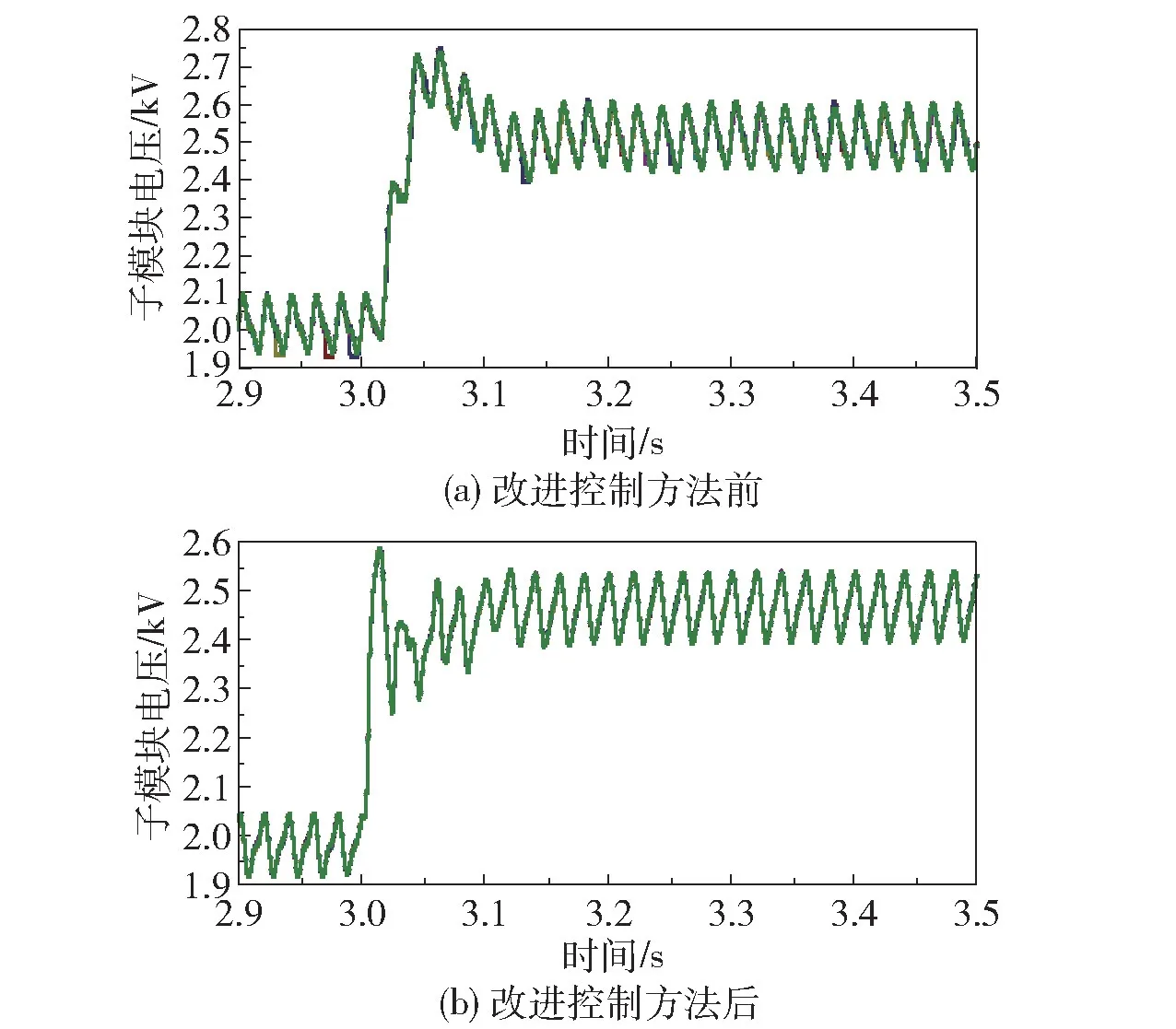
图19 改进控制方法前后的A 相子模块电压Fig.19 A phase submodule voltage before and after improving the control method
4 结论
本文针对目前MMC-HVDC 系统中存在的结构复杂、稳定性差、动态性能不能满足生产要求等问题,提出了一种基于外环模糊自适应PI 控制和内环模型预测控制的MMC - HVDC 控制方法。 在PSCAD 仿真平台搭建MMC-HVDC 系统模型,对改进后的MMC-HVDC 系统控制方法进行了仿真验证。 实验结果表明,本文提出的方法可以实时整定参数,减少系统计算量,并且减少资源占用,实现更精准的跟踪效果。
本文所提控制方法只在双端MMC-HVDC 系统三相对称结构下进行了实验验证,后续将对基于MMC 的多端系统的三相不对称情况作进一步分析验证。

