一种改进的无模型自适应控制优化方法
刘 康 陈 娟
(北京化工大学 信息科学与技术学院, 北京 100029)
引 言
现代工业过程的大型化、规模化和集成化使得实际工业现场环境也变得更为复杂[1],对象的非线性、系统的干扰和不确定性使得系统建模困难,传统的基于模型的控制方法 (model based control,MBC)难以应用。 在此背景下,基于数据驱动的控制理论和方法得到了国内外学者的广泛关注[2]。
与MBC 方法不同的是,数据驱动控制方法(data driven control, DDC)仅利用被控系统的输入输出数据来设计控制器,其中典型的基于数据驱动理论的方法有神经网络控制(neural network control,NNC)、迭代学习控制(iterative learning control,ILC)、无模型自适应控制(model-free adaptive control,MFAC)。 这些基于系统输入输出数据设计的控制方法也是对传统MBC 方法的重要补充。 神经网络控制因其能够利用神经网络算法充分逼近任意复杂的非线性映射关系,从而在一些复杂的工业过程中得到了广泛应用[3]。 但是神经网络在模拟非线性时容易发生过拟合现象,需要凭借经验去设计合理的神经网络结构,使得系统的稳定性和收敛性难以保证。 迭代学习控制是一种基于具有重复特性工业过程的控制算法,其本质思想是通过上一批次的误差信息进行学习,进而降低控制算法对模型的依赖,因结构较为简单、控制效果显著而被大量学者研究[4-6]。 然而在实际的工程应用中, 对于迭代学习控制如何选取满足系统收敛条件的学习增益,是一个值得进一步研究的问题。 无模型自适应控制能够充分利用被控系统的输入输出数据,将原系统转换成一个等价的动态线性化数据模型[7]。 相比于上述两类控制方法,MFAC 方法有着更强的鲁棒性和自适应能力。
目前,无模型自适应控制已得到广泛研究。 王文佳等[8]针对自动泊车问题提出了一种基于无模型自适应控制的泊车方案,该方案的优点在于仅利用泊车过程中的输入输出数据,对于其他车型也有很好的自适应性。 姚文龙等[9]针对环卫车辆轨迹跟踪问题,提出一种基于动态线性化的无模型自适应迭代学习控制方案,与传统迭代学习控制算法相比,其引入的无模型自适应控制器使得系统具有更好的鲁棒性。 Ma 等[10]针对多智能系统的协同控制问题,提出一种分布式无模型自适应控制算法(distributed model free adaptive control, DMFAC),通过紧格式动态线性化的数据模型和攻击补偿机制实现了多智能体的分布式协同控制。 Wu 等[11]针对风电系统中的不确定性问题,提出一种基于静止同步补偿机制的无模型自适应控制方法,该方法利用动态线性化建模降低了实际风电系统中由实际环境的不确定性所导致的误差,使得电力系统能够适应不同的工作条件。 然而传统MFAC 方法的控制效果十分依赖于其控制器参数的设置[12],在整定参数过程中容易使系统的动态性能变差。
鉴于传统MFAC 方法对一类复杂非线性系统的控制性能不理想以及参数整定问题,本文提出一种改进的无模型自适应控制方法(IMFAC),该方法在传统MFAC 方法的基础上引入了输出变化量因子来改善系统的动态性能,并分析了该方法的稳定性和收敛性。 然后对IMFAC 方法的控制器进行优化,采用灰狼优化(grey wolf optimization,GWO)算法对IMFAC 的控制器参数进行寻优,进而得到了参数寻优后的IMFAC 方法(G-IMFAC)。 通过仿真对比了MFAC 方法、IMFAC 方法及G-IMFAC方法的性能,结果表明G-IMFAC 方法可以有效改善系统的控制性能。
1 传统的无模型自适应控制方法
在本文中考虑的是基于紧格式动态线性化的无模型自适应控制方法。 一般的单输入单输出离散时间非线性系统如下。
式中,u(k)、y(k)分别是系统在k时刻的输入和输出,k=0,1,2,…,nu、ny分别是非线性系统的输入阶数和输出阶数,f(·)是未知的非线性系统。 现对该非线性系统做出如下假设。
假设1 除有限时刻点外,非线性系统(1)对于第(ny+2)个变量存在连续的偏导数。
假设2 非线性系统(1)满足广义Lipschitz 条件,即对任意时刻的采样点k1≠k2、k1,k2≥0 和u(k1)≠u(k2),有
式中,c>0 是一个常数。
由文献[7]可知在满足假设1、2 的情况下一定存在一个被称为伪偏导数的时变参数ϕc(k)∈R,使得非线性系统(1)可以转化成如下紧格式动态线性化模型。

式中,yd是给定的参考信号,^ϕc(k)是ϕc(k)的估计值。 由式(4)和式(5),通过最优化方法可以得到基于紧格式动态线性化的MFAC 方法如下[5]。
式中,λ>0、μ>0 是权重系数,ρ∈(0,1]、η∈(0,1]是步长因子,^ϕc(1)是^ϕc(k)的初始值,ε>0 是一个充分小的正数。 式(7)的PPD 重置算法可以使^ϕc(k)对时变参数有着更强的跟踪能力。
2 改进的无模型自适应控制方法
2.1 方法描述
由上述传统的MFAC 方法可知,其控制性能准则函数J1仅考虑了误差e(k)和控制器输出变化量Δu(k)。本文对控制性能准则函数J1加入系统输出变化量Δy(k+1),使其具有更好的动态性能。 在式(4)的基础上,考虑如下改进的控制性能准则函数
式中,ω>0 是输出变化量权重因子。 引入的(y(k+1) -y(k))2项可以衡量系统的动态性能。对式(8)关于Δu(k)求偏导有

与传统的MFAC 方法相比,IMFAC 方法可以通过调节ω来进一步改善系统的动态性能,当ω为0时,IMFAC 即为MFAC。 由式(7)和式(11)可知IMFAC方法的5 个控制器参数(η、ρ、λ、μ、ω)之间相互耦合。 为了选取最优的IMFAC 控制器参数,本文将采用灰狼优化算法对IMFAC 方法的控制器参数进行寻优。
2.2 稳定性分析
在假设1 和假设2 的基础上继续作出如下假设。
假设3 非线性系统(1)的伪偏导数ϕc(k)符号恒定,不失一般性,假设ϕc(k)恒大于0。
在非线性系统(1)满足假设1、2、3 的情况下,对于给定的常值参考信号yd有如下定理。


故系统的输出跟踪误差是收敛的,定理1 得证。
定理2 证明 通过分析可得,由给定期望信号yd是一个常数,又由式(16)中的e(k)有界,可以得到系统输出序列{y(k)}是有界的,故只需证明系统控制输入序列{u(k)}有界,证明过程如下。
由式(11)对Δu(k)取绝对值得

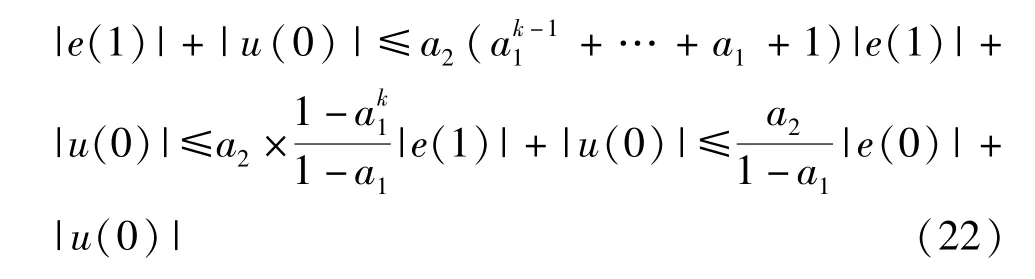
显然|u(k)|也是有界的。 综上所述,系统的控制输入序列{u(k)}和输出序列{y(k)}都是有界的,系统也是BIBO 稳定的,定理2 得证。
3 基于灰狼优化算法的参数寻优
3.1 灰狼优化算法
灰狼优化算法是一种新兴的群智能优化算法[13],因算法结构简单、调整的参数少,具有较强的收敛能力,所以本文采用该算法对IMFAC 的控制器进行优化。
在灰狼群体的社会等级中,遵守着如图1 所示的社会支配等级关系,其中α是领头狼,β是副领头狼,δ是普通狼,γ是底层狼。 灰狼群体的捕猎活动主要在领头狼α的决策和领导下展开。 在灰狼优化算法设计中,α为最优解,β为次优解,δ为第三优解,γ为其余解。
图1 灰狼社会支配等级Fig.1 Social domination levels of the grey wolf
3.2 适应度函数设计
灰狼优化算法适应度函数的设计直接关系到寻优结果。 一般来说,评价一个控制系统性能要综合考虑系统的动态性能和稳态性能。 传统时间乘误差绝对值积分(integral of timed absoluted error,ITAE)指标虽然能使系统获得较好的响应时间,但其超调量较大,因此本文在传统ITAE 指标的基础上加入对超调量σ和调节时间ts的权重控制,并以如下综合指标作为灰狼优化算法的适应度函数。

设由NSGA-II 算法得到3 个指标的Pareto 前沿构成的评价矩阵为X=(xmn)M×3,其中m=1,2,…,M是Pareto 最优解,n=1,2,3 是对应的优化指标。利用熵权法[15]对3 个指标计算权重的步骤如下。
步骤1 首先对3 个指标的数据进行标准化

其中权重wn体现了各指标的信息熵含量,熵权值越大表示该指标对综合指标的作用越大。 利用熵权法确定了适应度函数的表达式后,基于灰狼优化算法的IMFAC 参数寻优流程如图2 所示。
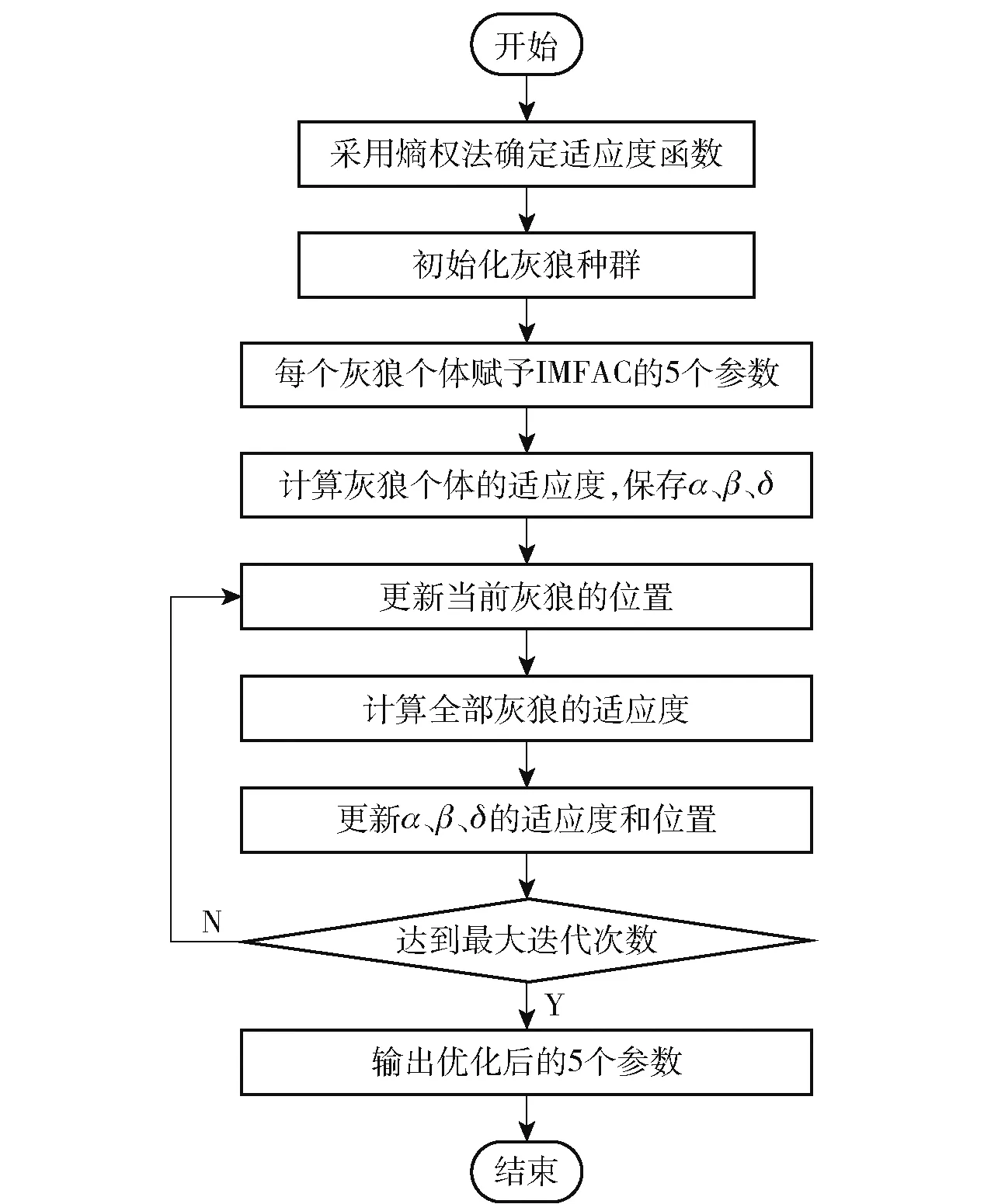
图2 参数寻优流程Fig.2 Flow chart of parameter optimization
4 仿真分析
设有非线性系统如下。
该非线性系统的初始条件为u(1) =u(2) =0,y(1) = -1,y(2) =1,ϕc(1) =2,ε=0.000 01,给定常值参考轨迹信号为yd=5,传统MFAC 方法的参数选为η=1,ρ=0.8,λ=1,μ=1。
(1)IMFAC 方法
为了分析IMFAC 方法的有效性,在保持η、ρ、λ、μ的选取与传统MFAC 方法一致的情况下,IMFAC 方法中分别选取w=0.1、w=0.5、w=1 和w=4,两种方法的仿真结果及控制器的输出如图3、4所示。
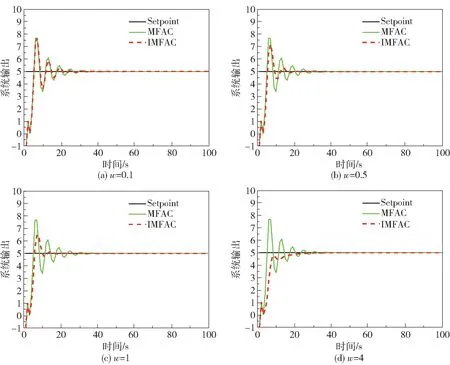
图3 系统输出Fig.3 System output
由图3 不难发现,IMFAC 方法中w选取得越大,系统的超调量越小,但是当w选取过大时,也会使系统的响应变慢,但整体的控制性能都较MFAC方法优越,显然w需要结合实际工艺需求进行选取。 由图4 可知,IMFAC 方法的控制器输出也更稳定。
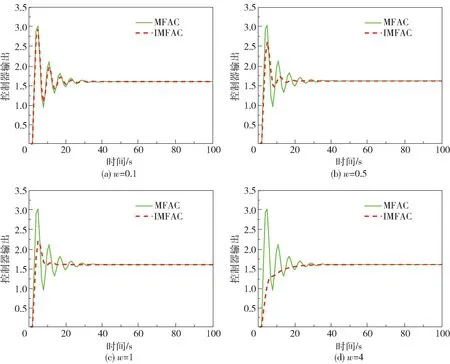
图4 控制器输出Fig.4 Controller output
(2)G-IMFAC 方法
G-IMFAC 方法采用灰狼优化算法对其控制器参数寻优,并针对灰狼优化算法适应度函数中3 个优化指标权重分配的问题,通过计算各个优化指标的信息熵来确定其权重。 该方法首先采用NSGAII 算法计算得到ITAE 指标、超调量σ和调节时间ts的Pareto 前沿(图5),再根据式(24) ~(26)计算这3 个优化指标的权重,结果如图6 所示。
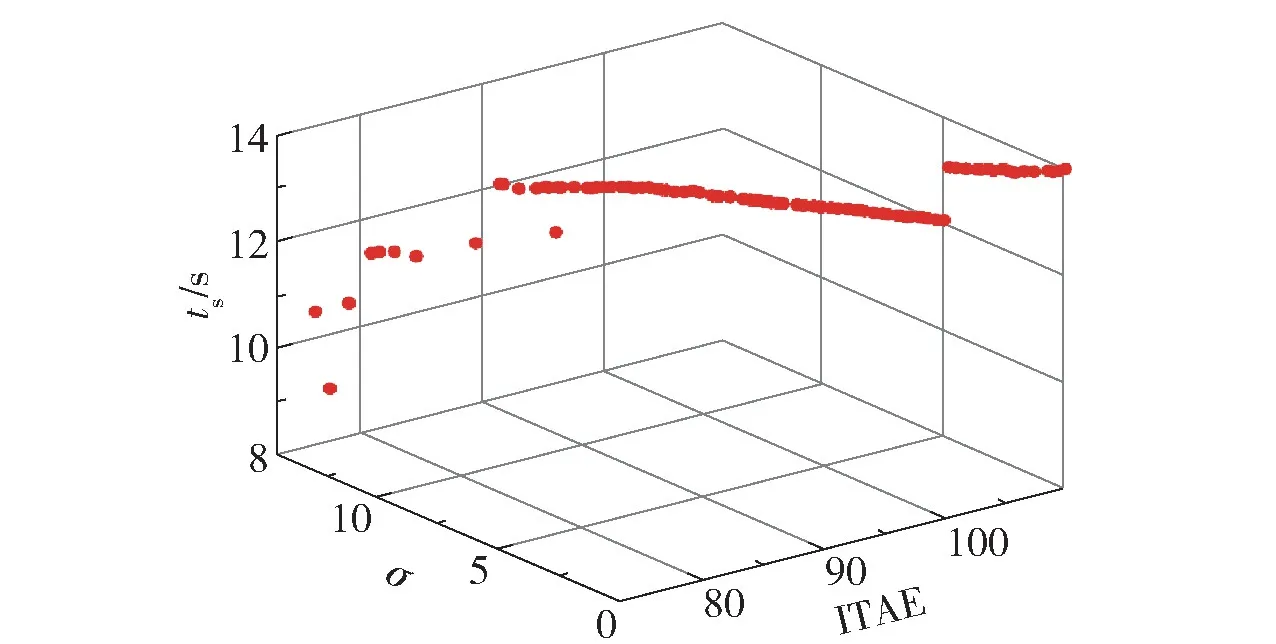
图5 3 个优化指标的Pareto 前沿Fig.5 Pareto frontier of three optimization indicators
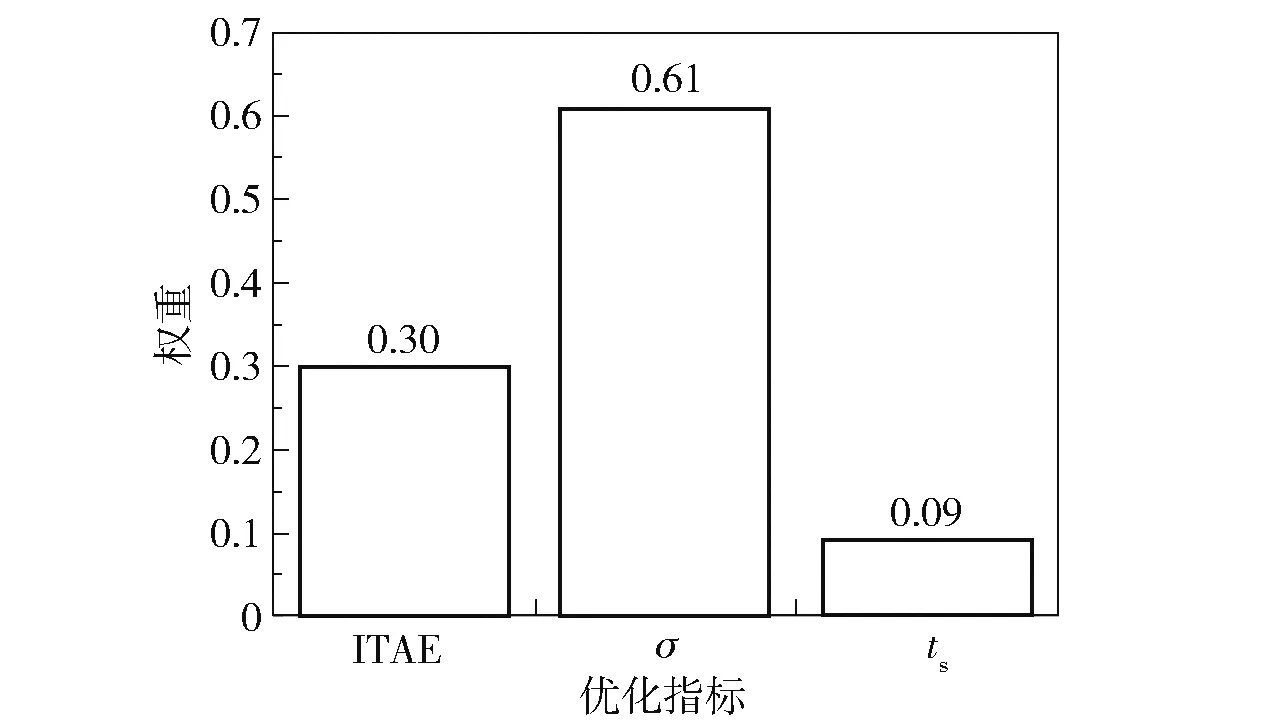
图6 3 个指标的权重Fig.6 Weights of the three indicators
由图6 可以得到灰狼优化算法适应度函数各指标的权重[w1,w2,w3] =[0.3,0.61,0.09],再采用灰狼优化算法对IMFAC 方法的5 个控制器参数进行寻优,适应度函数的收敛过程和参数寻优过程如图7、8 所示。
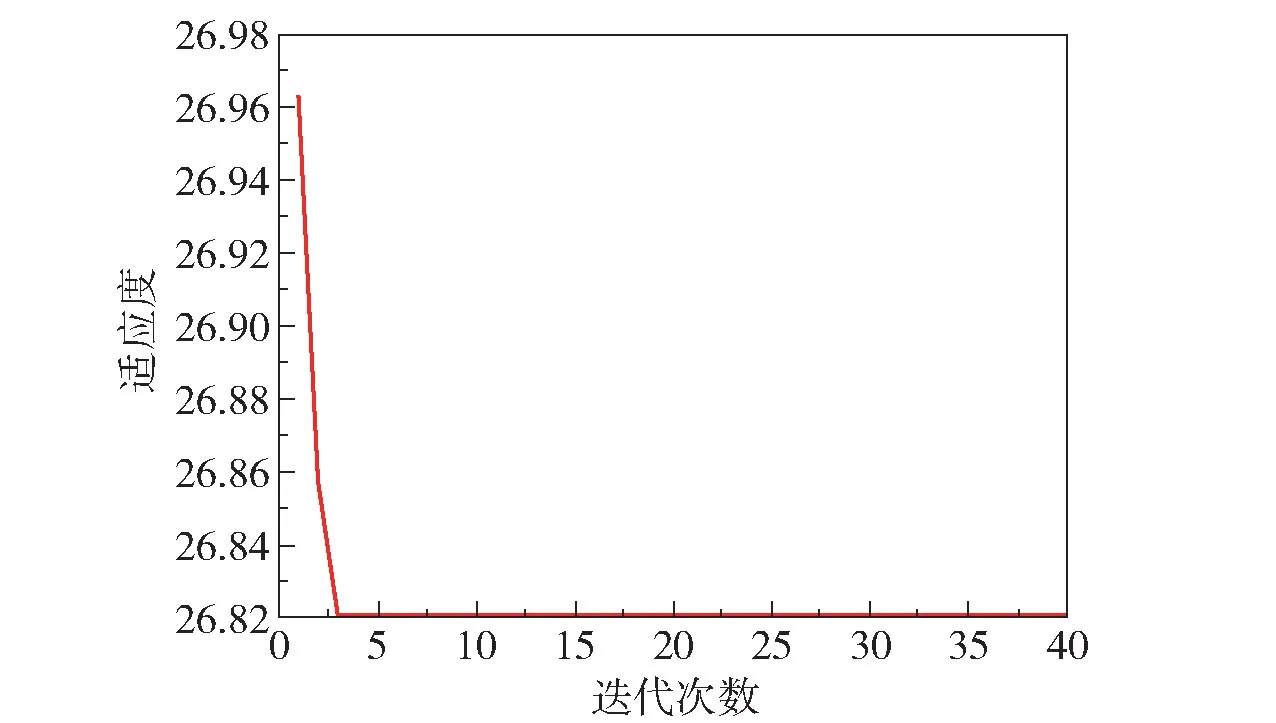
图7 优化算法适应度函数Fig.7 Optimization algorithm fitness function
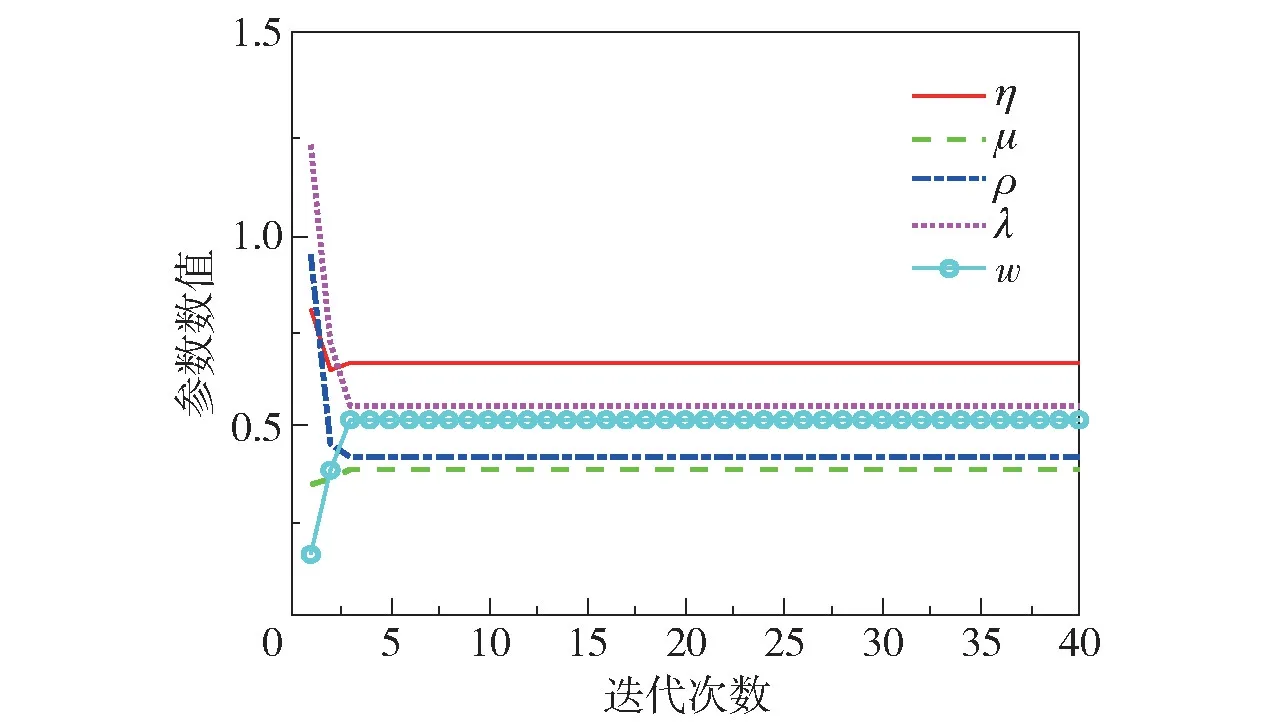
图8 参数寻优过程Fig.8 Parameter optimization process
由图7、8 可知,采用灰狼优化算法得到的GIMFAC 方法中 的5 个参数值[η,μ,ρ,λ,w] =[0.65,0.37,0.41,0.54,0.50]。
为了验证G-IMFAC 方法的有效性,在k>50时对系统加入一个单位阶跃干扰信号,此时传统MFAC 方法、IMFAC 方法(w=0.5)、G-IMFAC 方法的系统输出和控制器输出变化如图9、10 所示。
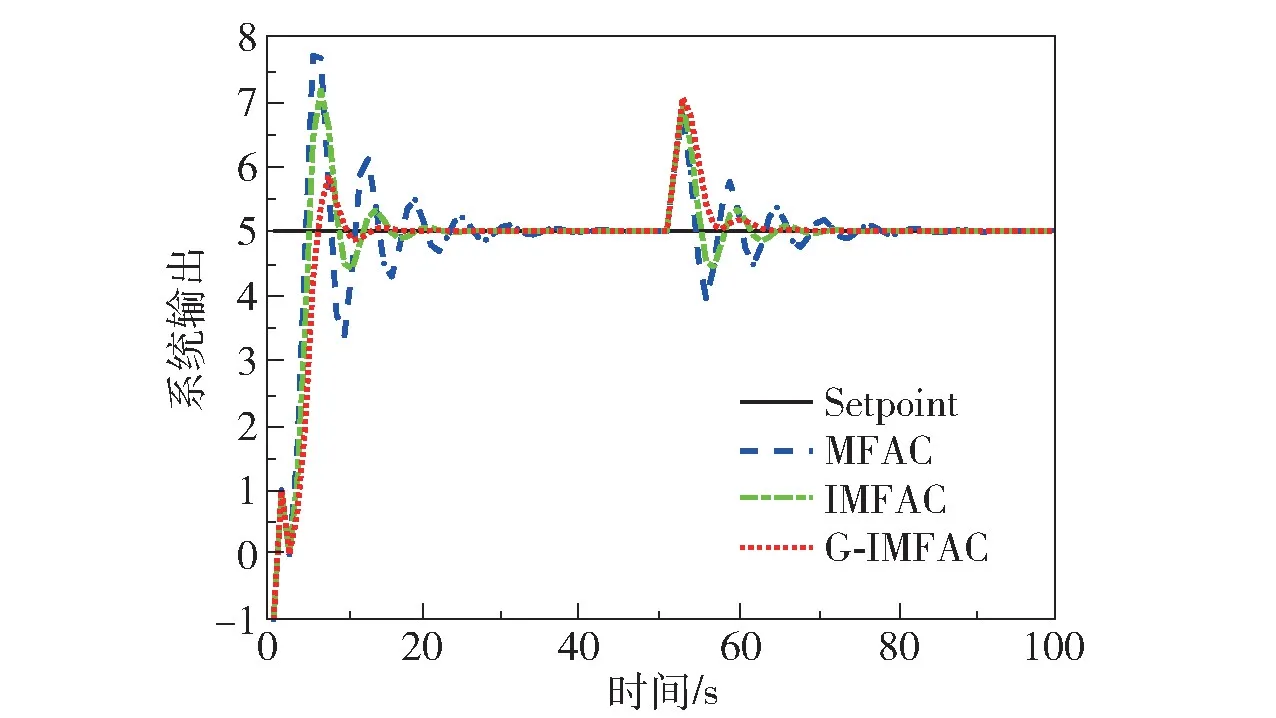
图9 系统输出Fig.9 System output
由图9 和图10 可知,在系统未加入扰动时,GIMFAC 方法有着更小的超调量和更短的调节时间;当加入单位阶跃干扰时,G-IMFAC、IMFAC、MFAC 3种方法恢复至稳定的时间(稳态值±5%内)分别为56 s、60 s、65 s,显然G-IMFAC 方法能更快克服单位阶跃干扰的影响。

图10 控制器输出Fig.10 Controller output
为了进一步比较3 种方法的控制性能,计算得到加入单位阶跃干扰后3 种方法的ITAE 如表1 所示,显然G-IMFAC 方法的ITAE 最小,表明其拥有更好的控制性能。

表1 3 种方法的ITAE 比较Table 1 ITAE comparison of the three methods
5 结论
本文针对一类复杂非线性系统提出了一种改进的MFAC 方法,该方法针对传统MFAC 控制律引入输出量变化因子,并分析了IMFAC 方法的稳定性和收敛性。 然后对控制器进行优化,采用灰狼优化算法对其参数寻优,并针对灰狼优化算法适应度函数中3 个优化指标权重分配的问题,通过计算各个优化指标的信息熵来确定其权重。 仿真结果表明,相比传统的MFAC 方法,本文提出的G-IMFAC 方法具有更小的超调量、更快的调节时间以及更低的ITAE 指标,控制系统的控制性能得到了显著提升。

