伽菲尔德与勾股定理

袁秀 整理

1876年的一个傍晚，伽菲尔德走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。由于好奇心驱使，伽菲尔德循声向两个小孩走去。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是，伽菲尔德便问他们在干什么。

只见那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”伽菲尔德答道：“是5呀。”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”伽菲尔德不假思索地回答道：“那斜边的平方一定等于5的平方加上7的平方。”

小男孩又说道：“先生，你能说出其中的道理吗？”伽菲尔德一时语塞，竟无法解释了，心里很不是滋味。

于是，伽菲尔德不再散步，立即回家，潜心探讨小男孩给他留下的难题。

他经过反复地思考与演算，终于弄清楚其中的道理，并给出了简洁的证明方法。

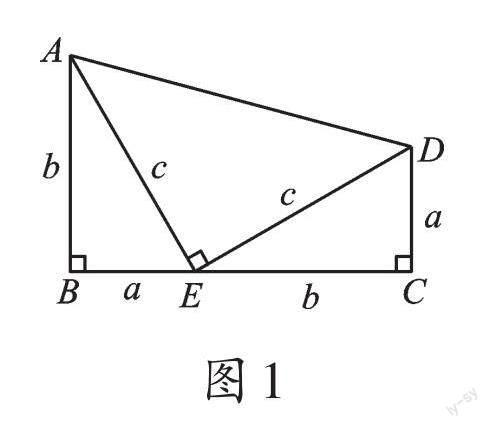
他是这样分析的，如图1所示：

S梯形ABCD=[12]（a+b）2

=[12]a2+ab+[12]b2。

S梯形ABCD=S△ABE+S△CDE+S△ADE

=[12]ab+[12]ab+[12]c2

=ab+[12]c2。

由梯形面积相等，得[12]a2+ab+[12]b2=ab+[12]c2，所以[12]a2+[12]b2=[12]c2，即a2+b2=c2。

1876年4月1日，伽菲尔德在《新英格兰教育日志》上發表了他对勾股定理的这一证法。

1881年，伽菲尔德就任美国第二十任总统。后来，人们为了纪念他，就把这一证法称为“总统”证法。

（作者单位：江苏省南京市钟英中学）