初中数学课堂提问策略初探
王昕
《义务教育数学课程标准(2022年版)》指出,数学教师要选择能引发学生思考的教学方式,重视单元整体教学设计,强化情境设计和问题提出。问题的提出应引发学生认知冲突,激发学习动机,促进学生积极探究,增强学生解决真实问题的能力,树立学好数学的自信心,养成良好的学习习惯。因此,教师应合理地提高数学课堂问题的质量和有效性,提升课堂教学质量。
一、激发学习兴趣,提高学生思维活跃度
学生只有对数学产生兴趣,才能学好数学。在实际教学过程中,教师要想让学生更加积极地参与到课堂教学中来,最好的方法就是激发学生的学习兴趣,提高学生的主观能动性。教师应针对学生的年龄、理解能力、心理特点去提问,把数学问题与学生感兴趣的内容结合起来,活跃课堂气氛,促进学生主动思考、积极探索,提升课堂教学效果。以苏科版数学七年级上册“从问题到方程”一课的教学片段为例。
师:大家最喜欢的中国篮球运动员是谁?
生:姚明。
师:你为什么喜欢姚明?
生:姚明个子高、球技好、训练刻苦、很幽默……
师:这里有一道关于姚明打篮球的题目,大家愿不愿意尝试一下?
生:愿意。
例1 著名篮球明星姚明在一场NBA篮球比赛中24投14中,得到28分,其中三分球4投3中。请问姚明两分球投中多少个?(篮球知识:篮球比赛中罚球投中一个得一分。)
【设计意图】前两个问题看似与本节课无关,实际上是针对七年级学生的心理特点和兴趣爱好,调动学生学习的积极性,让学生对例1产生浓厚的兴趣,提升学生思维活跃度,便于学生在解题时充分地开动脑筋,思考出正确的解题方法。
二、类比学习内容,构建完整知识体系
类比思想是通过两个研究对象属性、特征、关系、形式等方面的类似之处,推断出它们在其他方面也可能存在类似的一种推理方法。类比思想是将已经学习的知识与即将探索的新知识联系起来的一种重要的学习思想。在教师精心设计的提问中,学生不仅探究了新的知识,同时也对已学的知识进行了回顾,在提高学习能力的同时,也构建了一个完整的知识体系,并在学习过程中不断完善、优化。以苏科版数学八年级下册“矩形、菱形、正方形”一课的教学片段为例。
师:我们知道,矩形、菱形都是特殊的平行四边形,它们之间存在着一定的联系,请同学们回顾矩形的第一个判定方法。
生:有一个角是直角的平行四边形是矩形。
师:那么请大家猜想一下菱形的第一个判定方法是什么?
生:一组邻边相等的平行四边形是菱形。
师:很好。下面谁来回顾一下矩形的第二个判定方法。
生:三个角是直角的四边形是矩形。
师:为什么是三个角,而不是四个角?
生:如果三个角是直角,那么第四个角一定是直角。
师:请大家猜想一下菱形的第二个判定方法是什么?
生:四条边都相等的四边形是菱形。
师:这个猜想是否正确,我们尝试来证明一下。(证明过程略。)
师:矩形的第三个判定方法是什么?
生:对角线相等的平行四边形是矩形。
师:类似的,同学们猜想一下菱形的第三个判定方法是什么?
生:对角线互相垂直的平行四边形是菱形。
师:同样的,我们来证明这个猜想的正确性。(证明过程略。)
【设计意图】本节知识的理解对学生来说是比较困难的,因为需要掌握的定义、定理很多。如果教师能通过问题将前后的知识点结合起来,让学生掌握它们之间的联系与区别,便能方便学生更好地理解知识的内涵。在渗透数学思想的同时,也帮助学生更好地构建完整的学科知识体系。
三、引导探究思路,培养良好学习方法
在初中阶段的学习中,很多学生感到数学比较难学,特别是在一些有难度的章节中,某些知识点更不容易理解和掌握。这时候往往需要教师指导学生去探索,需要教师根据实际教与学的情况设计有梯度的问题,通过这些问题给学生思考的台阶。问题的设计要由易到难,从学生容易接受的问题开始,一步一步地扶着学生走上台阶,不怕台阶多,关键要让学生踩上来、踩得对、踩得稳。问题的设计还要环环相扣,让学生从中发现某种联系和规律,发现突破难点的关键所在。这些问题的设置可以引导学生探索正确的思路,让学生学会思考,循序渐进地掌握知识,感受到学习数学的成就感,最终达到学会学习、善于学习、乐于学习的目的。以苏科版八年级下册“图形的旋转”一课的教学片段为例。
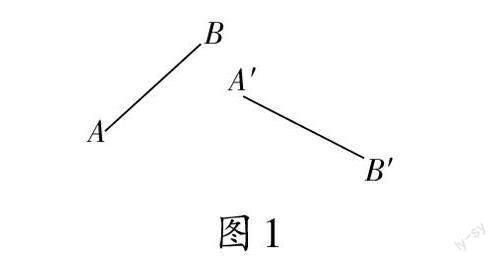
例2 如图1,画出AB绕点O旋转后,线段AB的对应线段是A′B′,试确定旋转中心点O的位置。
师:同学们,如果我们不能马上想出解题的方法,那么大家可以猜想一下旋转中心O的位置大概在哪里?在你认为最可能的地方先画一个点找找感觉。
生:大概在线段AB 、A′B′的下方。
师:你认为你画的这个旋转中心要满足什么样的条件?
生:到点A和点A′的距离相等,到点B和点B′的距离相等。
师:为什么?
生:如果这个点是旋转中心,那么对应点到旋转中心的距离相等。
师:你能找出到A、A′两点距离相等的点吗?
生:在线段AA′的垂直平分线上。
师:你能找出到B、B′两点距离相等的点吗?
生:在线段BB′的垂直平分线上。
师:你能找出同时满足上面两个条件的点吗?
生:线段AA′的垂直平分线与线段BB′的垂直平分线的交点。
师:那么你能确定旋转中心点O的位置了吗?
生:可以。
【设计意图】本节课学生已经学习了如何画已知图形绕某个点旋转一定的角度得到的对应图形,但对由已知图形和对应图形找旋转中心还是感到比较困难的。因此,教师可以先让学生进行猜想,再通过设置问题串讓学生逐步找到突破口。这样的过程不仅帮助学生解决了问题,而且还展示了解决问题的正确思考方式,让学生掌握正确的学习方法。
在数学课堂教学中,许多教师的教案上并没有细化到每一次提问,课堂上经常出现为了提问而提问,提出的问题没有针对性的现象,不少提问没有对教学产生有效的作用,脱离学生的实际。其实,课堂教学中的每一次提问都很重要,只有提高课堂教学中提问的技巧,才能使数学课堂教学更高效,从而促进学生核心素养的生成和发展。

